基于改進粒子群算法的自由曲面輪廓度評定

萬 潤,王 琳,盛步云

(武漢理工大學 a.機電工程學院;b.湖北省數字制造重點實驗室，武漢 430070)

0 引言

近年來，隨著制造業的發展，自由曲面零件越來越廣泛應用于汽車、飛機、大型船舶等工業領域。曲面的加工質量直接關系到產品的質量和使用壽命，因此對自由曲面零件進行高效率與高精度的檢測和輪廓度誤差評定有著重要的研究意義[1]。

對于復雜曲面輪廓度的評定，依據算法原理主要可以分為二類，一類是基于最小二乘原理，最具代表性的是在1992年提出的最近點迭代算法[2]，常用于曲面定位問題中。一類是基于最小條件的最小區域法，要求包容全部測點的理論曲面等距面的距離最小，由于一般曲面的表達式未知，且計算量復雜，多采用啟發式優化算法解決這類非線性優化問題，如遺傳算法、粒子群算法[3-4]等, 但遺傳算法在進行輪廓度誤差評定時，由于局部搜索性能較差，容易產生早熟收斂的問題，而且在進化后期搜索效率不高，在解決大規模計算量問題上比較費時；而粒子群算法在運算后期則容易陷入局部最優。

在確定最小包容區域過程中，測量點到曲面的距離計算也是其中一個重要的問題[5-6]，文獻[5]用網格劃分曲面，通過不斷細分網格來逼近測點到曲面的實際距離，但必須已知曲面的函數表達式且計算過程復雜，難以平衡計算精度和效率，文獻[6]把空間點到自由曲面距離轉化為點到STL模型的有向距離，但沒有考慮到出現狹長三角面片的情況，存在適應性缺陷。

為解決以上問題，本文采用一種基于天牛須搜索的粒子群優化算法，以測點集與理論輪廓面達到最佳匹配為目標，尋找一組平移、旋轉變換矩陣來確定理論曲面的最小包容區域，并且針對出現狹長三角面片的情況做了優化處理，進一步簡化了測點投影點與三角面片關系判定條件，提高了算法的實用性和適應性。

1 自由曲面輪廓度評定模型的建立

1.1 曲面輪廓度誤差的定義及關鍵步驟

根據GB/T 1958-2004，輪廓度評定要求滿足最小條件原則，即所有測量點均位于上下兩包絡面邊界所限定的包容區域內，且包容區域的寬度或直徑為最小，其誤差值是包容被測曲面輪廓且距理論曲面輪廓法向距離最小的兩曲面間的寬度。

輪廓度評定一般需要解決兩個關鍵步驟的問題，一是計算測點到復雜理論曲面的最小距離，二是建立復雜曲面輪廓度誤差評定的數學模型并求解。針對步驟一，將曲面CAD模型轉換為STL模型，測點到曲面的最小距離就簡化為尋找距離測點最近的三角面片的問題；針對步驟二，根據最小條件原則和齊次坐標變換理論建立相應的輪廓度評定數學模型，并應用基于天牛須的改進粒子群算法求解。

圖1 曲面輪廓度誤差示意圖

1.2 點到自由曲面STL模型最短距離計算

STL模型是通過一系列三角面片來逼近CAD模型的，其數據文件主要包含二進制和文本兩種格式，主要描述三角面片的頂點坐標數據信息和單位法矢量數據信息[7]。文獻[6]通過判斷測點投影點與STL模型三角面片的位置關系，來求取其到曲面的最短距離，相較于傳統的需要已知曲面表達式的分割逼近法適用性更高。但存在兩點不足，一是投影點與三角面片位置關系的判斷條件不夠簡化，二是如果STL模型中存在狹長的三角面片，則以測點到三角面片頂點的最近距離為擇優目標篩選出的三角面片集不一定包含距離測點最近的三角面片，導致算法失效。針對上述不足一，采取向量運算代替相對繁瑣的角度量計算，將投影點與三角面片關系整體分為三類情形來判斷，針對不足二，選擇測點到三角面片頂點和中心點兩者之間的最小距離，綜合篩選三角面片集。

計算測點到自由曲面距離的具體步驟如下：

步驟1：計算測點Pi(xi,yi,zi)到每個三角面片頂點及中心點的距離，標記距離最近點為Qi點。

步驟2：如果點Q為三角面片頂點，則搜索以Q點為頂點的所有的三角面片并放入集合S內；如果點Q為三角面片中心點，則搜索與該三角面片共頂點的所有三角面片并放入集合S內。

步驟3：分別計算測點Pi到集合S內三角面片的距離，依據測點投影的位置，測點到三角面片的距離計算有以下三種情形：

情形1：投影點Sp在三角面片內部，此時測點P到三角面片的最短距離就是測點P到投影點Sp的距離。

情形2：投影點Sp在三角面片外部，但處于三角形某一邊延長線與另一邊延長線的區域范圍內，此時最短距離就是測點到這兩條邊的共頂點的距離。

情形3：測點投影在三角面片外部，但處于三角形某一邊與另一邊延長線的區域范圍內，此時測點P到三角面片的最短距離就是測點到三角面片上該邊的距離。假設投影點Sp的位置不滿足上述兩者的情形，則必然滿足情形3，只需計算測點P到三角面片三條邊的距離，其中最小值即為測點到該三角面片的最短距離。

按照以上3步計算點到所有三角面片的距離，以最小值作為點到曲面距離。

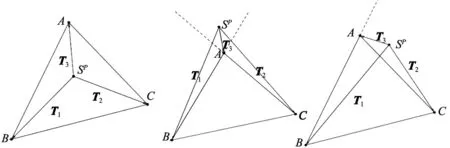
(a) 情形1 (b) 情形2 (c) 情形3圖2 投影點和三角面片關系示意圖

1.3 曲面輪廓度評定的數學模型

由于在實際測量過程中存在系統誤差，測量坐標系與設計坐標系難以完全重合，測量曲面相對于理論曲面會有一定的偏移與擾動。依據最小條件原則，只有當測點集與理論輪廓面達到最佳匹配時，才能使包容所有測量點的兩理論等距曲面之間的距離最小，因此必須對測點集進行剛性平移、旋轉坐標變換，使得最大變動量最小化。設實測曲面上的測點為pi(xi,yi,zi),i=1,2,…,n，其中n為測量點數量，其坐標變換矩陣為：

T=Trans(δx,δy,δz)Rot(x,α)Rot(y,β)Rot(z,γ)

(1)

式中，平移變換矩陣為：

(2)

旋轉變換矩陣為：

(3)

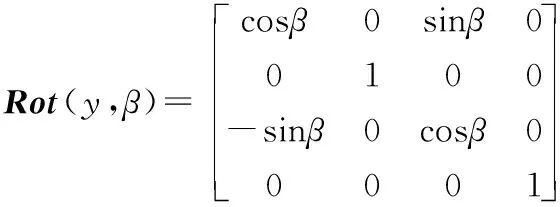
(4)

(5)

其中，δx,δy,δz為實際加工曲面沿理論曲面坐標系x,y,z軸的平移量，α,β,γ為實測曲面繞理論曲面坐標系x,y,z軸的旋轉量。

測量點經過坐標變換后的新坐標為：

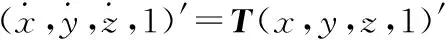
(6)

則最小區域法評定復雜曲面輪廓度誤差的數學模型為：

f=min{max[2di(δx,δy,δz,α,β,γ)],i=1,2,3,…,n}

(7)

其中，di(δx,δy,δz,α,β,γ)為測點到理論設計曲面的距離，由模型可以看出，輪廓度誤差的評定過程實質上是一個多元非線性尋優過程，要求尋找一組最優的變換參數，使所有測點到曲面的最大距離最小。

2 基于天牛須搜索的粒子群優化算法

2.1 BAS算法(天牛須)

天牛須搜索算法是2017年提出的一種高效的智能優化算法[8]，當甲蟲捕食或尋找獵物時，它會用兩只觸角隨機地探索附近的區域，當位于一側的觸角探測到高濃度的氣味時，甲蟲就會轉向同一側，否則，它就會轉向另一側。雙觸角甲蟲的搜索行為可以與待優化的目標函相關聯，從而形成新的優化算法。和遺傳算法、粒子群算法等智能算法類似，相比較傳統的微分類優化算法，天牛須算法同樣可以在缺乏具體的函數表達式和最快下降方向等信息基礎上實現高效尋優與求解。具體的算法流程如下：

(1)假設天牛可以隨機向任何方向前進，隨機生成方向向量，標準化：

(8)

其中，n為待優化參數的維度。

(2)計算天牛左右須的坐標也即左右觸角的位置：

xtr=xt+dtb
xtl=xt-dtb

(9)

其中，xt為t時刻天牛的位置，dt是t時刻天牛質心到觸須的距離，xtl為第t次迭代時的左側觸須坐標,xtr為第t次迭代時的右側觸須坐標。

(3)根據左右兩須對應的函數值，決定天牛下一時刻移動位置：

xt+1=xt+δtbsign(f(xtr)-f(xtl))

(10)

δt為t時刻的步長，f為待優化目標函數，sign代表符號功能。

(4)步長與搜索距離更新：

dt=ηddt-1+d0
δt=ηδδt-1

(11)

ηd和ηδ分別為搜索距離和步長的更新衰減系數，d0表示兩觸角之間的初始距離。

2.2 基于天牛須搜索的改進粒子群優化算法

粒子群算法雖然在收斂速度上具有優勢，但側重于種群和粒子本身的歷史經驗對每一個粒子的影響，而忽略了在搜索過程中粒子自身對空間環境的判斷，也無法對粒子的速度進行動態的調節，容易陷入局部最優。針對上述問題，可以選擇引入天牛須的思想提高粒子的自主尋優和全局搜索能力[9-10]。

相較于標準粒子群算法，基于天牛須搜索的改進粒子群算法中的每個粒子就相當于BAS中的一只天牛，雖然其初始位置和速度不變，但在每次的迭代過程中，天牛位置的更新規則不再只由歷史最優值和當前全局最優值所決定，而是引入天牛須搜索的思想，添加了天牛自身對周圍環境的判斷。

(1)位置更新時，按照PSO和BAS的方式各自更新后加權得到新的位置。也就是，利用了BAS的觸須方向和步長，同時也利用了粒子的速度：

(12)

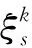
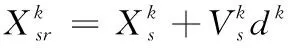
(13)

曲面輪廓度評定的具體過程如下：

(1)初始化參數，設置種群規模為N，最大迭代次數n，參數維度m，位置更新權重λ，初始步長d0，觸須之間長度初始值d1。

(2)隨機初始化天牛的位置x和速度v，確定適應度函數，獲得天牛群體的個體最優值和全局最優值。

(3)根據式(12)和式(13)計算天牛的下一步位置與速度。

(4)更新天牛搜索步長和兩觸須之間的長度，并計算更新后的天牛群的個體最優值和全局最優值。

(5)判斷是否滿足迭代終止條件，若滿足，則返回當前全局最優值，否則返回步驟(3)繼續搜索，直至達到最大迭代次數。

3 仿真分析

為了測試改進后的粒子群算法對比標準粒子群在評定曲面輪廓度上是否有更高的準確性，選用自由曲面一進行仿真實驗，該STL模型由242個三角面片和165個頂點構成。在曲面上均勻選取400個理論測點，考慮到存在的系統誤差，將理論測點沿x,y,z軸平移0.1 mm、0.3 mm、-0.6 mm，逆時針旋轉-0.05 rad、-0.04 rad、0.07 rad，并添加服從正態分布N(0,0.04)的隨機性矩陣作為加工誤差，得到模擬實測點集。即：

(14)

其中，

設計曲面和仿真測點分布如圖3a所示，圖3b為改進后的粒子群算法完成模型求解后重新定位的測點分布，6個最優變換參數結果如表1所示。

(a) 定位前的測點分布

(b) 定位后的測點分布圖3 自由曲面一仿真測點定位前后分布圖

表1 自由曲面一定位的6個參數

選用自由曲面二進行仿真實驗，該STL模型由1776個三角面片，954個頂點構成。在曲面上隨機選取400個理論點，添加系統誤差e=[0.1,0.2,-0.1,-0.01,-0.02,0.02]，同樣添加服從正態分布N(0,0.04)的隨機性矩陣作為加工誤差，得到模擬實測點集合。設計曲面和仿真測點分布如圖4所示，圖4b為改進后的粒子群算法完成模型求解后重新定位的測點分布，6個最優變換參數結果如表2所示。

(a) 定位前的測點分布

(b) 定位后的測點分布圖4 自由曲面二仿真測點定位前后分布圖

表2 自由曲面二定位的6個參數

根據測點到曲面的距離模型計算輪廓度誤差，對于自由曲面一，改進后的粒子群算法和粒子群算法求得的輪廓度誤差分別為1.130 8 mm和 1.136 7 mm。如果是均勻提取100個點作為理論測點，則計算的輪廓度誤差分別是0.951 4 mm和1.036 1 mm。對于自由曲面二，改進后的粒子群算法和粒子群算法求得的輪廓度誤差分別為1.226 1 mm和 1.262 0 mm。由以上兩個實驗可知基于天牛須搜索的改進粒子群評定的曲面輪廓度結果更加精確。

4 結束語

為了提高曲面輪廓度評定結果的準確性，建立了輪廓度誤差評定的數學模型，并采用引入天牛搜索思想的改進粒子群算法進行求解。將測點到自由曲面的距離轉化成測點到STL模型的距離，并對于存在狹長三角面片的情況作了補充處理，同時也簡化了測點投影點與三角面片關系的判斷條件。通過仿真實驗驗證與對比，采用基于天牛須搜索的粒子群算法相對于標準粒子群可以有效提高曲面輪廓度誤差的評定精度。

DOI：10.5430/ijrc.V1n1p1.