基于改進蟻群算法的AGV多目標路徑規劃*

李傳奇，黃衛華,b,c，章 政 ,b,c，金 震，張子然

(武漢科技大學 a.機器人與智能系統研究院；b.冶金自動化與檢測技術教育部工程研究中心；c.信息科學與工程學院，湖北 武漢 430081)

0 引言

自動導引車(Automated Guided Vehicle，AGV)作為一種自動化程度高、靈活性好、抗干擾能力強的移動機器人，廣泛應用于現代工業自動化物流倉儲系統[1]。路徑規劃[2]是AGV調度系統研究和應用的關鍵問題之一。一般而言，物流倉儲系統具有高效快速的運輸需求，合理的路徑規劃方法對AGV能夠實現有效、安全的自動行駛具有重要作用。

常規AGV路徑規劃大多是以單個目標作為尋優目標，如：時間最少、路徑最短、拐點最少或者目標點全遍歷等。文獻[3]以路徑長度為優化目標，改進蟻群算法的啟發因子及全局信息素分布方式，規劃AGV行駛路徑；而文獻[4]以最少轉折點為目標，采用多方位搜索法，避免路徑轉折點過多導致AGV配送時間增加；文獻[5]以最短路徑長度為首要目標進行規劃，再從所得路徑中選取轉折點最少的作為最終路徑；文獻[6]則以最小化搬運完成時間為目標，定義了AGV沖突優先級，提出一種生成無路徑沖突的規劃算法，提高AGV的作業效率。

隨著 “綠色物流”[7]的發展，基于單目標函數的路徑規劃方法對于描述AGV路徑規劃問題具有一定局限性。除常見規劃目標外，運輸安全性、能源消耗等因素也被視為AGV運行性能指標，實際運行時，這些因素之間相互影響、制約，存在互斥性，即一個目標的優化可能會導致其他目標的退化。例如，最短路徑可能是AGV緊貼著障礙物以降低安全性為代價的路徑；最安全的路徑可能是拐點最多的路徑，會導致AGV行駛時間和能源成本增加。因此，以多個目標作為物流倉儲系統路徑規劃的準則，需綜合考慮多種因素的共同影響，實現AGV在多個目標共同優化作用下的自主路徑規劃。

本文綜合考慮物流倉儲系統路徑規劃的快速性、穩定性和安全性需求，設計了一種基于改進蟻群算法的AGV多目標路徑規劃算法。首先，構建子目標函數，并采用熵權法確定子目標權值以構建路徑評價函數，以最小化評價函數值為總目標搭建多目標路徑規劃模型；然后，通過改進蟻群柵格轉移方式及引入非支配排序算法，提高蟻群多目標優化能力；最后，基于仿真結果，證明了本文所設計的多目標路徑規劃算法用于動靜態地圖下AGV路徑規劃的可行性和有效性。

1 基于熵權法的AGV多目標路徑規劃建模

考慮到物流倉儲環境的復雜性，路徑的低危險率保證AGV在行駛過程中遠離障礙物，減少與障礙物碰撞的可能性；更短的避障等待時間意味著AGV能更快的完成作業。因此，本文構建AGV多目標路徑規劃模型，綜合考慮路徑長度、轉角和、危險率和避障等待時間作為AGV路徑規劃的子目標，并采用熵權法確定子目標權重。

1.1 各子目標模型的建立

柵格法簡單高效、易于實現和表達不規則障礙物，本文采用柵格法[8]對倉儲環境進行建模。描述如下：將AGV工作環境等分為a行a列個柵格，柵格大小能完全容納機器人。無障礙物柵格為可行柵格(白色表示)，有障礙物柵格為不可行柵格(黑色表示)，障礙物小于一柵格時，按一柵格處理。移動機器人在柵格間的移動可看作一個質點，并假設每次都停留在柵格的中心位置。

(1)路徑長度

路徑長度最短能節約AGV工作時間及運行成本。路徑長度子目標函數f1如下：

(1)

式中，n表示路徑經過的總節點數(包含起點和終點)；xi、yi分別表示節點i的橫縱坐標；L(i,i+1)為節點i、i+1之間的距離，如圖1所示。

圖1 路徑長度、轉角示意圖

(2)轉角和

AGV在轉彎時會減速以避免車速過大導致車體側翻或甩落所運載的貨物。當轉彎較多時，AGV頻繁的進行減速控制，且轉角過大會增加低速運行的時間。因此選擇轉角和作為規劃子目標之一，對轉角和進行有效約束能節約工作時間、減少轉彎導致的輪胎磨損等機械損耗。轉角和函數f2如下：

(2)

式中，θ(i,i+1,i+2)表示路徑轉角，如圖1所示。

(3)危險率

AGV通過車載的導航傳感器實時定位并由環境傳感器感知周圍障礙物信息。由于傳感器自身精度缺陷易導致AGV所獲得的定位信息和環境信息間存在一定誤差，特別是距障礙過近時，測量誤差可能會造成AGV與障礙物間產生摩擦或碰撞。

AGV與障礙物距離越近，危險率越高，當AGV距離障礙物兩柵格以上時，受障礙物影響較小可忽略。危險率函數f3如下：

(3)

其中，

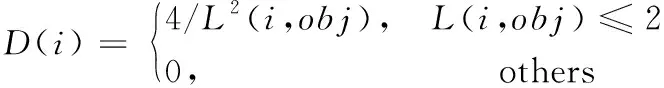
式中，D(i)表示節點i處的危險率；obj為離節點i最近的障礙物柵格中心。

(4)避障等待時間

當AGV遇到動態障礙物時，需暫停運動并等待障礙物離開。避障等待時間函數f4如下：

(4)

式中，b代表總避障次數，T(o)代表第o次避障等待時長。

1.2 多目標路徑規劃模型的建立

(5)

理想值均取所有待評價路徑中該子目標的最小值。

同時，采用曼哈頓距離描述各子目標函數值與理想值間的接近程度。由式(1)～式(5)構建AGV多目標路徑規劃評價函數F為：

(6)

由此AGV多目標路徑規劃模型為：

Y=minF

(7)

其中，Y為路徑規劃總目標,目的是求一條從起點到終點的連續無碰撞且評價函數值最低的路徑。

1.3 基于熵權法的評價函數權值確定

熵權法是客觀的權值計算方法，通過信息熵計算出各指標的熵權，再利用熵權對權值進行修正，與其它權值計算方法相比評價結果具有較好的客觀性[9]。考慮式(1)～式(4)所示子目標對評價函數影響不完全相同，無法主觀衡量子目標間的優劣、占比程度，因此選用熵權法根據實際路徑信息計算式(6)中w1～w4的值，具體步驟如下：

步驟1：構建原始數據矩陣。由m個待評價路徑，s(1≤s≤4)個子目標構成原始數據矩陣R′：

(8)

步驟2：標準化處理。旨在消除指標間的量綱差異，記標準化處理后的矩陣R=(ruv)m×s。因路徑長度值、轉角和、危險率、避障等待時間均越小越好，為負向指標，則標準化處理公式為：

(9)

步驟3：計算第v個子目標的熵值hv。

(10)

其中，

步驟4：確定各子目標的權值大小。

(11)

2 改進多目標蟻群算法

傳統蟻群算法[10-12]主要對路徑長度進行優化，本文對蟻群算法做出改進，將蟻群算法擴展至多目標函數優化。

2.1 改進螞蟻擇路方式

柵格地圖中蟻群運動可看成從當前柵格中心向下一柵格中心轉移過程的積累。螞蟻的下一可轉移柵格是與當前相鄰的八個柵格，標號如圖2所示，偶數柵格表示直向轉移柵格，奇數柵格表示斜向轉移柵格。若AGV向3號或5號柵格轉移，可能出現AGV與障礙物柵格頂點摩擦或碰撞的情況，影響AGV正常運行。對下一柵格選取方式改進如下：

斜向擇路時，驗證AGV當前位置與下一斜向柵格中心連線的垂線上的兩個最近柵格是否有障礙物，若有，則將斜向柵格標記為不可轉移柵格。如圖2所示，可將3號和5號柵格標記為不可轉移柵格。

圖2 蟻群擇路柵格模型

2.2 改進信息素播撒機制

由于信息素濃度只受路徑長度影響，其它子目標對蟻群指引作用較小，蟻群多目標尋優能力不足。本文利用非支配排序算法對每次迭代的可行路徑分層，層數越靠前，表明該層路徑至少在一個或多個子目標上很優，給予該層中的路徑更多的信息素增量，從而使多個目標共同指引蟻群尋優。

非支配排序算法的核心思想便是支配比較。將路徑支配的概念描述如下：路徑A、B均為可行路徑，若A在某個子目標上優于B，且其余子目標上均不弱于B(可以相等)，則稱路徑A支配路徑B；否則路徑A與B是非支配關系。由一系列不被其他路徑所支配的路徑組成最優路徑集合。

利用非支配排序對路徑分層，步驟如下：

步驟1：每次迭代結束后，將可行路徑存入集合G中，并保存路徑子目標函數值。

步驟2：對于G中的任一路徑p，都與其余路徑進行支配關系比較，統計支配路徑p的路徑數目np、被p所支配的路徑集合Sp。若np=0，則表示路徑p不受其它任何路徑支配，將其分入T1層。

步驟3：對于T1中的路徑p，將Sp集合中的每一個成員q的支配計數nq減1。若nq=0，則表示路徑q除了受T1層路徑支配外，不再受其它路徑支配，將q分入T2層。

步驟4：依步驟3方式，將對應路徑分入T3層。

步驟5：剩余路徑分入T4層。

劃分完畢后，有如下關系：同層路徑之間相互非支配；對Tl+1(l=1,2,3)層中的任一路徑，在Tl層中至少存在一條支配它的路徑。

前層路徑更優，應給與更多的信息素增量以加強對后續螞蟻的指引作用，同時弱化后層路徑信息素增量，改進如下：

(12)

其中，

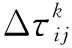
3 多目標路徑規劃算法流程

綜上所述，本文所設計的基于改進蟻群算法的多目標路徑規劃步驟如下：

步驟1：采用柵格法對物流倉儲環境建模。

步驟2：確定子目標函數及多目標路徑規劃模型。

步驟3：初始化參數。初始化蟻群參數及最優路徑集合Q，Q用于存放最優路徑。

步驟4：蟻群迭代。開始此次迭代，依據改進的螞蟻擇路方式確定可行柵格，利用輪盤賭法選出下一個節點，直至終點或螞蟻“死亡”。

步驟5：非支配排序。依據式(1)～式(4)計算可行路徑子目標函數值。利用非支配排序算法對路徑分層。

步驟6：信息素更新。依據式(12)更新信息素。

步驟7：更新最優路徑集合Q。對于排序后T1層中的路徑p，如果p對于集合Q來說是非支配的，則加入集合Q，并刪除Q中被p所支配的路徑。

步驟8：迭代次數更新。迭代次數d=d+1，當迭代次數最大時，結束迭代，否則返回步驟4。

步驟9：權值計算。輸出最優路徑集合Q，利用熵權法計算子目標權值。

步驟10：輸出最終路徑。依據式(6)計算路徑評價函數值，取最小評價值路徑為最終輸出路徑。

4 實驗結果與分析

4.1 靜態環境下實驗結果與分析

物流倉儲環境下貨物分布較為規整，構建如圖3所示的柵格地圖，柵格行列數a=30；起點坐標(0.5,0.5)，終點坐標(29.5,29.5)。設置蟻群最大迭代次數Nmax=50，蟻群數量M=100。地圖中無動態障礙物，暫不考慮避障等待。利用本文改進多目標蟻群算法得到最優路徑集合Q，Q中的路徑如圖3所示，路徑信息如表1所示。

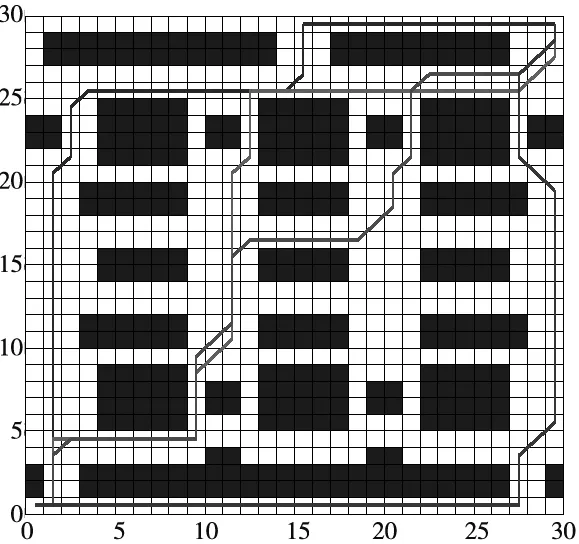
圖3 靜態環境改進蟻群路徑圖

表1 靜態環境改進蟻群路徑信息表

由圖3和表1可以看出，改進的多目標蟻群算法得到的路徑1～4分布范圍較廣，有沿著地圖中部斜向指向終點的路徑1、4，也有沿著地圖邊緣的路徑2、3，各路徑之間相互非支配，優勢均不相同，路徑2轉角和最小，路徑3危險率最低，路徑4長度最短，路徑1性能最均衡。

路徑1、4因為多斜向行走，路徑長度較其它兩條路徑更小，但受地圖中心障礙物影響，轉角較多，平滑性較其它兩條路徑有所下降；同時，路徑2前半段緊貼障礙物，危險率在4條路徑中最高。

上述結果表明：靜態環境下，本文改進的蟻群算法對各子目標均能有所優化，能引導蟻群多目標尋優，實現AGV多目標路徑規劃。

在相同的蟻群參數、柵格環境及擇路方式下，利用傳統蟻群算法尋路，結果如圖4所示，路徑信息如表2所示。

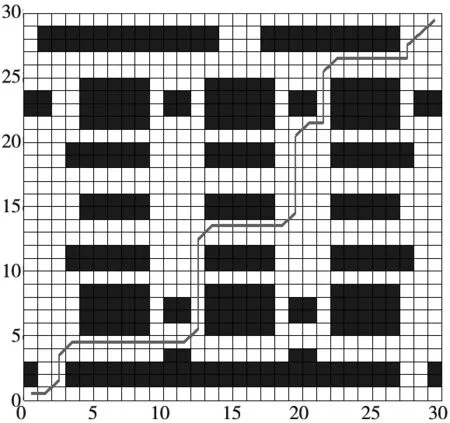
圖4 靜態環境傳統蟻群路徑圖

表2 靜態環境傳統蟻群路徑信息表

由于傳統蟻群算法中路徑長度對尋優起主導作用，圖4中路徑5斜向行駛至終點。與改進的多目標蟻群算法路徑1～4相比：路徑5較路徑1在長度上減小了5.96%，轉角和增加了35.76%，危險率增加了16.15%；較路徑2在長度上減小了9.84%，轉角和增加了137.5%，危險率增加了5.59%；較路徑3在長度上減小了6.25%，轉角和增加了90.06%，危險率增加了30.17%；較路徑4在長度上增加了1.13%，轉角和增加了5.59%，危險率增加了16.15%。

可以看出，路徑5相比于改進的多目標蟻群算法路徑1～3，小幅縮短了路徑長度，但是轉角和、危險率上都有所上漲，路徑5在提升路徑長度的同時，損失了路徑的平滑性和安全性；且路徑5各方面性能均比路徑4差。

利用熵權法對5條路徑的信息進行計算，得到各子目標權值如表3所示，最終評價函數值如表4所示。

表3 靜態環境子目標權值表

表4 靜態環境評價函數值表

從表4可以看出，較傳統蟻群算法路徑5，路徑1～4的評價函數值更小，路徑更優，且路徑3評價函數值最小，僅為1.85，最趨近于理想值，為靜態環境下的最優路徑。可得出，靜態環境下，本文改進的蟻群算法能進行有效的多目標路徑尋優，較傳統蟻群算法所得路徑綜合性能更優。

4.2 動態環境下實驗結果與分析

物流倉儲環境中可能出現人員走動、貨物擺放位置臨時改變等動態情況，在上述靜態環境中添加動態障礙物以研究本文改進蟻群算法所得路徑在動態環境中的適應能力。為方便研究，對動態障礙物作如下設計：在如圖5所示的每個黃色方框內隨機產生一個動態障礙物；其大小能被1柵格完全容納；動態障礙物活動范圍即為黃色方框區域；動態障礙物隨機產生，沿水平方向勻速直線運動，觸碰到活動邊界時沿鏡面反射方向折返。

圖5 動態障礙物活動范圍圖

AGV分別沿路徑1～5前進，每次避障等待時間為5 s。最終各子目標信息如表5所示。

表5 動態環境路徑信息表

從表5可得，路徑1、2、5均遭遇一次動態障礙物，進行了一次避障等待，路徑4避障2次，路徑3避障0次。權值計算如表6所示，路徑評價值如表7所示。

表6 動態環境子目標權值表

表7 動態環境評價函數值表

由表7可以看出，路徑3評價值為1.48，最趨近于理想值路徑，為最優路徑；傳統蟻群算法所得的路徑5評價值最大，路徑綜合性能最差。路徑4雖然比路徑5多一次避障等待，但評價值較路徑5更低，路徑更優。可以得出，若地圖中出現了少量動態障礙物，本文改進的多目標蟻群算法所得路徑仍然具有更強的適應性，且其綜合性能、整體評價較傳統蟻群路徑更優。

5 結論

根據AGV運行需求選取子目標，提出一種基于改進蟻群算法的AGV多目標路徑規劃方法，該方法改變柵格選取方式、利用非支配排序算法改進信息素增量、利用熵權法確定權值。仿真結果表明動靜態環境下本文設計算法能有效進行多目標路徑尋優，所得路徑分布廣、性能高，綜合評價更優。