基于復合多尺度排列熵的軌枕狀態診斷方法

邵志慧，楊 儉，袁天辰，伍偉嘉

(上海工程技術大學 城市軌道交通學院，上海201620)

我國高速鐵路已進入快速建設和規模化運營時期，成果舉世矚目，高鐵已成為我國最重要的國家名片之一。然而，鐵路系統在長期服役的過程中，受到列車荷載、惡劣的環境和其內部應力等外因和內因的作用下，各種故障日益顯現，如有砟軌道的典型故障軌枕空吊、道床翻漿等嚴重威脅著列車的行車安全。目前，國內外主要依靠軌檢車和人工定期檢測來完成針對軌道故障的檢測和軌道的日常養護，主要缺點是勞動強度大、效率低、漏檢率高[1]，若沒有及時地發現軌道的故障，則有可能導致列車脫軌傾覆等無法挽回的后果。因此，對軌道結構的故障進行實時監測、故障判斷和故障等級預警具有科學和現實意義。

由于軌道各層級結構之間的連接不是完全剛性的，當軌道系統中的某一部件出現故障時，整個軌道結構的動力學特性將會發生改變，基于這一特性，可以通過分析軌道結構在列車作用下的振動響應來判斷其故障。因此，如何從軌道結構的振動響應中提取出故障信息是識別軌道故障的關鍵。近年來，許多國內外學者將近似熵[2]、樣本熵[3]、排列熵[4]、多尺度排列熵[5]等應用在故障識別領域，并獲得了不錯的識別效果。文獻[6]通過提取機械一維振動數據的近似熵來表示原始信號的動態特征信息，并通過分類器準確地識別了故障類型。文獻[7]結合集合經驗模態分解和樣本熵提取了自動機振動信號的故障特征，并利用粒子群算法優化的支持向量機對故障進行了診斷，試驗表明，這一方法能夠有效地對自動機故障進行識別。文獻[8]為了能夠對機械設備中的粘彈性夾層的老化狀態進行自動識別，通過小波包變換對振動信號分解為多個頻帶，并從各個頻帶中提取了排列熵，以此作為支持向量機的輸入，準確識別出了不同結構的老化狀態。Huo 等[9]采用自適應多尺度排列熵對軸承振動數據進行特征提取，并將其作為支持向量機的輸入數據進行故障類型分類，最終結果證明該方法對不同故障類型、嚴重程度和信噪比水平下的軸承故障診斷的有效性。然而由于軌道系統服役環境復雜，跨度大等原因，針對軌道結構智能故障診斷方法的研究仍處于起步階段。

排列熵僅能從單一尺度上對時間序列的復雜度進行度量[10]，而多尺度排列熵(Multi - scale permutation entropy，MPE)能夠對時間序列進行多尺度衡量，從而表達出信號在多個尺度上的細節信息。但MPE受序列長度的影響較大，即時間序列的長度在粗粒化過程中會隨著尺度因子的增大而變短，從而導致計算出來的熵值誤差偏大和特征信息的缺失。為了解決MPE對序列長度依賴性較大的問題，鄭近德等[11]在2015年提出了CMPE 的概念，通過MPE模型的時間序列粗粒化方式進行改進，使得粗粒化后的序列更具有平滑性，并求取各個尺度上熵值的平均值作為最終的熵值，進而很好的保留了時間序列中的故障特征信息。因此，本文以有砟軌道的軌枕作為研究對象，通過研究道床結構板結時軌枕振動響應的動力學特性，提取軌枕振動信號時間序列的CMPE值，構建CMPE特征集，從而大大降低了數據的維度，為后續算法的運行提供了便利；將CMPE 特征集作為遺傳算法優化的支持向量機輸入，對不同情況的道床板結下的軌枕振動響應進行診斷，實現了對道床五種剛度和阻尼下的軌枕振動響應的識別。

1 軌枕故障數據仿真

1.1 車軌耦合振動模型設計

本文參考翟婉明院士的著作《車輛-軌道耦合動力學》(第4版)[12]，采用四軸二系懸掛整車模型，將軌道系統模擬成三層彈簧-阻尼連續彈性支承的軌道模型，以此建立車軌耦合模型。其中，為了簡化軌道模型，鋼軌采用的是連續彈性離散點支承的Euler梁，因此軌下基礎(道床-路基)則以各軌枕為支承點沿縱向離散分布，圖1 為設計的車輛-軌道耦合垂向振動模型。本文建立的車軌耦合模型中，軌道長度l=120 m，相鄰軌枕之間的間距ls=0.6 m。為了模擬軌枕的不同故障，文獻[12]給出了相應的解決方法，即通過對模擬的軌下基礎的剛度和阻尼進行賦值，便可以從理論上模擬出軌枕的不同故障。當道床出現了局部暗坑時，軌枕與道床之間就會有空隙，如果空隙太大導致該處的道床完全失去了對軌枕的支承能力，則可在模型中設置該處道床的剛度和阻尼為0；然而，若是道床出現了結構松散現象，則可以通過分別改變道床的剛度和阻尼系數來模擬結構松散的不同情況，剛度和阻尼系數的取值范圍在0.1～10之間。

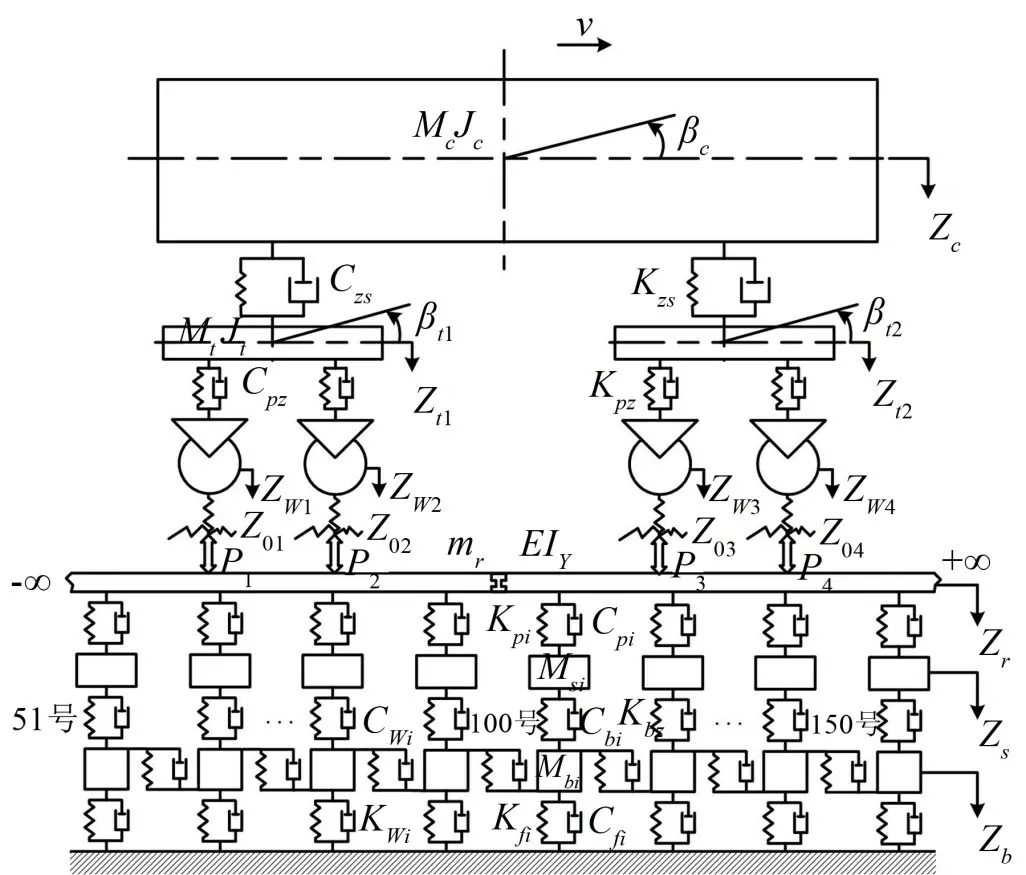
圖1 車輛-軌道垂向耦合振動模型

1.2 仿真軌枕振動響應

本文選取5 種軌道不平順譜，分別為irr1、irr2、irr3、irr4、irr5(irr:track irregularity)，作為仿真模型的激勵，對軌枕下道床剛度和阻尼進行賦值，模擬不同情況的道床結構松散，分別為S1:K’bi=Kbi、C’bi=Cbi，S2:K’bi= 3Kbi、C’bi= 3Cbi和S3:K’bi= 5Kbi、C’bi=5Cbi，S4:K’bi= 7Kbi、C’bi= 7Cbi，S5:K’bi= 9Kbi、C’bi=9Cbi。軌枕振動響應的具體描述如表1所示。

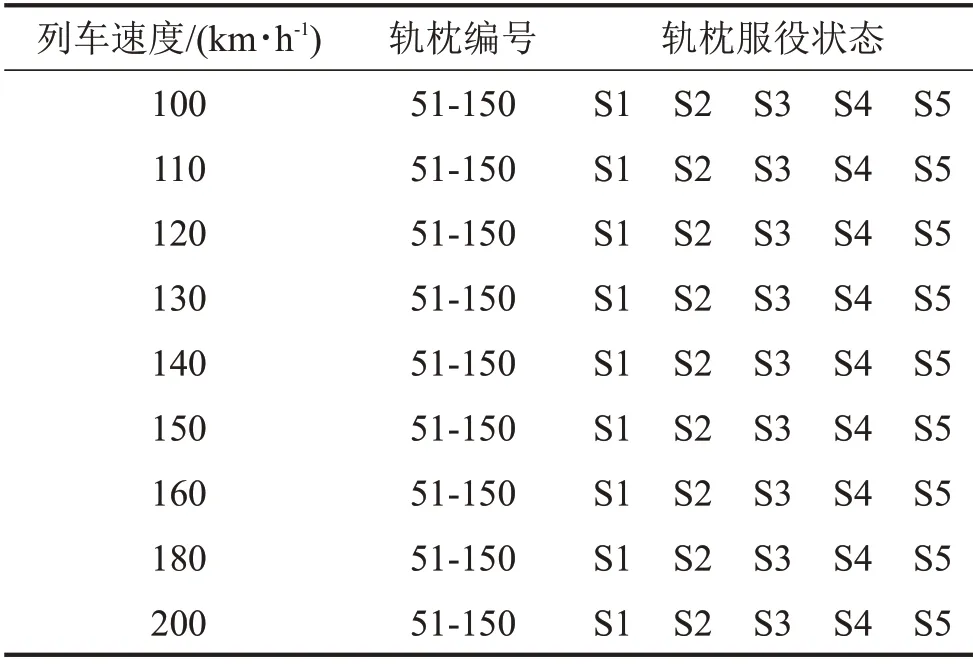
表1 各軌道不平順譜下的軌枕振動響應仿真數據描述

2 軌枕振動響應CMPE提取

2.1 CMPE的基本原理

排列熵是衡量時間序列在某一尺度上的復雜度的度量，排列熵值越大，時間序列的復雜度越大。若是僅從單一尺度上對時間序列進行描述，那么就有可能丟失一些重要的信息，從而無法對時間序列的復雜度進行準確的描述。而MPE 將時間序列在多個尺度上進行劃分，計算不同尺度因子上的排列熵，在不同的尺度上表征時間序列的復雜度。然而，MPE 對序列進行粗粒化劃分的過程中會隨著尺度因子的增大而不斷縮短每個尺度上序列的長度，進而導致振動信號的特征信息的缺失[13]。因此，為了解決MPE對序列長度過度依賴的問題，且當軌枕的支承層的剛度和阻尼發生變化后，軌枕振動響應的復雜度也會相應的發生變化，本文選擇鄭近德等提出的CMPE 對軌枕振動響應進行特征提取[11]。CMPE的流程圖如圖2所示。

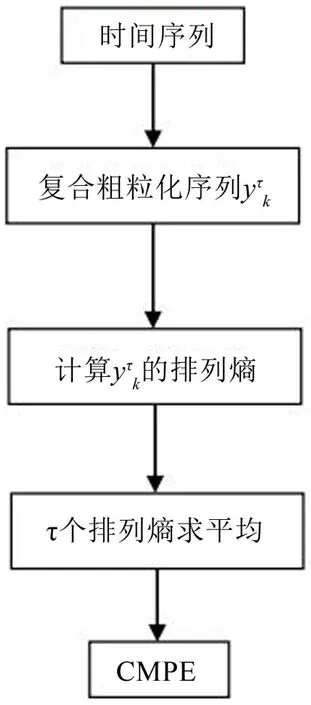
圖2 CMPE的流程圖

具體步驟如下：

(1) 對時間序列{X(i),i=1,2,…,N}進行粗粒化，N為序列長度，得到新的粗粒化序列：

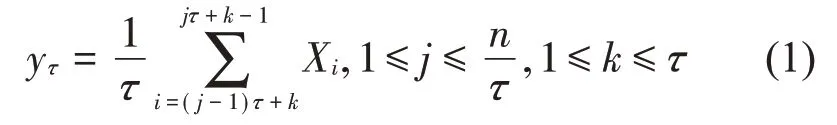
式中：τ為尺度因子，它決定了每段粗粒化序列的長度，即yj(τ)的長度為n/τ；

(2)計算每個尺度因子τ下粗粒化序列yj(τ)的排列熵值，再求τ個排列熵的平均值，那么每一個尺度因子下的CMPE值為：

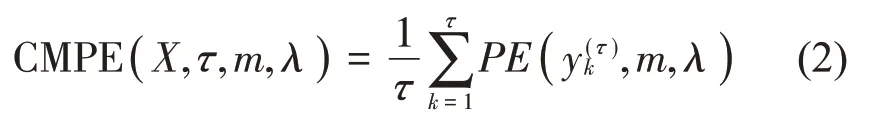
式(2)中：λ為延遲時間。CMPE 與MPE 的區別在于對時間序列的粗粒化方式，CMPE 對時間序列采取了復合粗粒化的方式進行了劃分，大大地降低了MPE對序列長度的依賴，最大限度地保留了時間序列中狀態信息。

2.2 軌枕振動響應特征提取方法的選擇

一般來說，對故障的識別會選用合適的分類器來實現，分類器的運算效率會隨著輸入數據維數的增多而減慢。因此，降低振動響應的維度，并保留信號中的有效信息是保證分類器識別效率的關鍵。

以上文仿真得出軌枕振動響應為原始數據，分別計算其MPE 和CMPE，比較這兩種方法對振動響應長度的敏感程度，以及說明CMPE 的優越性。本文基于文獻[14-16]，選取兩種算法的嵌入維數均為m=6，延遲時間均為λ=1，尺度因子τ=20。列車速度100 km/h和200 km/h時第100號軌枕振動響應的序列長度分別為N1=32 652 和N2=16 326，兩速度下5種振動響應的時域曲線如圖3 所示。分別計算irr1的激勵下這兩個振動響應的CMPE值和MPE值，比較時間序列長度對兩種算法的影響，結果如圖4所示。

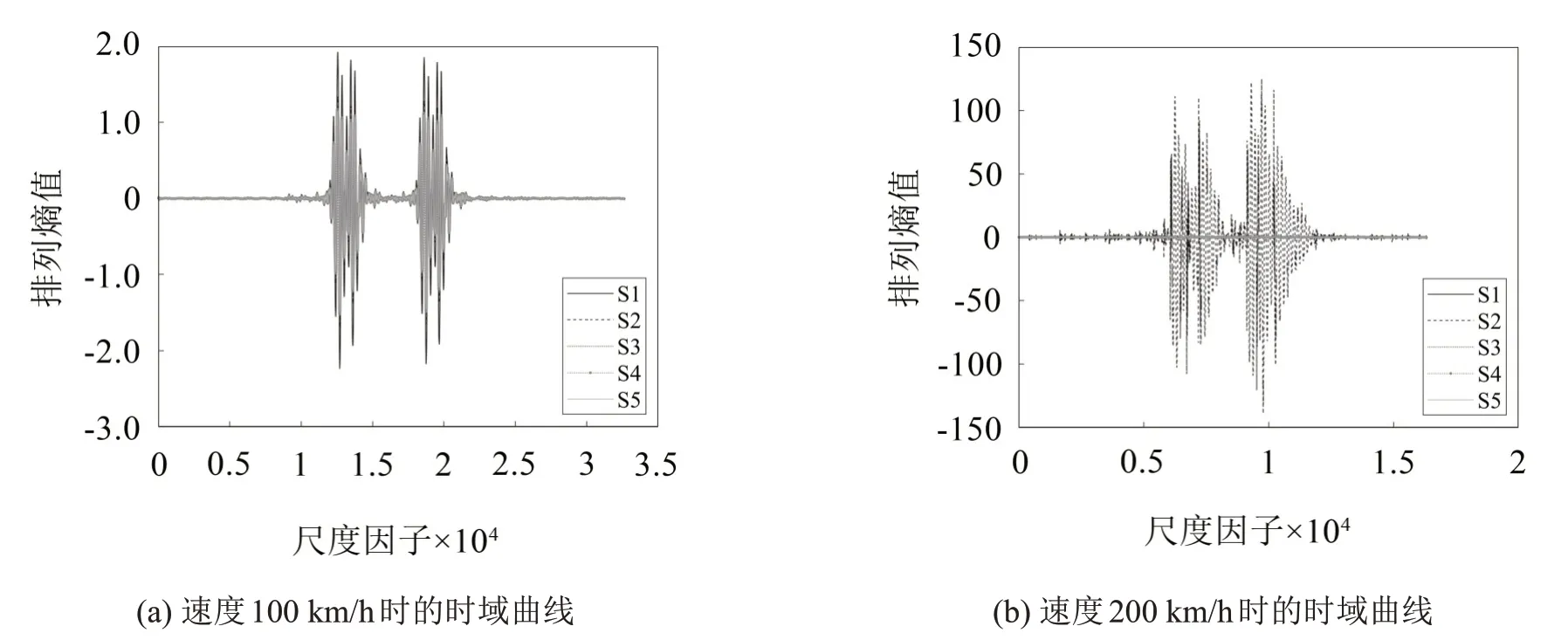
圖3 irr1激勵下，第100號軌枕的時域曲線

比較圖4(a)和圖4(c)可以看出，當振動響應序列長度縮短后，第100 號軌枕振動響應的CMPE 值仍然較為平滑，這說明CMPE算法在運算時較為穩定，對序列長度的依賴程度不高；而比較圖4(b)和圖4(a)，可以明顯的看到，雖然圖4(d)較圖4(c)不夠平滑，但還是能夠表現出熵值在尺度因子上的變化趨勢，而當序列長度由32 652縮短到16 326時，也就是比較圖4(b)和圖4(d)時，由圖4(d)可以看出，S2 在第15個尺度因子上出現了明顯的錯誤。這充分說明了CMPE 算法與MPE 相比，對序列長度的依賴性不高，得出的計算結果更具有魯棒性。因此，本文選擇CMPE算法來提取軌枕振動響應的特征。

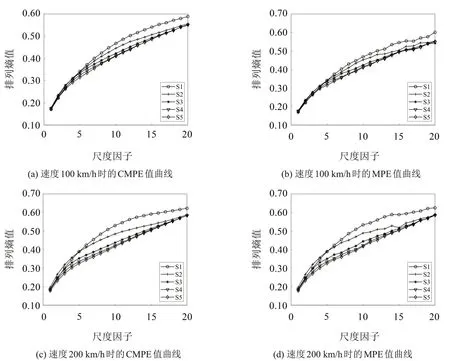
圖4 irr1激勵下，第100號軌枕的CMPE和MPE

3 軌枕狀態識別

3.1 支持向量機的基本原理

支持向量機作為傳統的分類器模型，其核心是找到一個能夠準確地將樣本分為兩類的最優超平面。而當需要分類的數據線性不可分時，將樣本向高維空間投影，這樣可以實現在高維空間中對樣本進行劃分，進而解決了樣本線性不可分的問題。然而，當樣本本身維度較高時，向高維空間投影很有可能會導致維度爆炸。為了解決這一問題，引入了核函數這一概念，目前國內外普遍采用的核函數是高斯徑向基核函數(Radial basis function，RBF)，其表達式如式(3)所示。

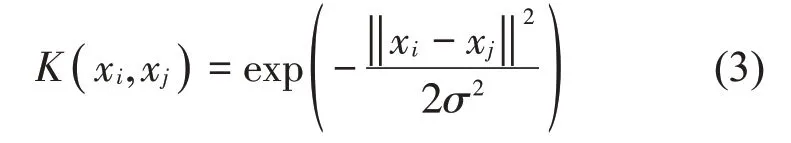
式(3)中：σ為高斯徑向基核函數的寬度。

核函數作為影響支持向量機分類效果的關鍵因素，懲罰因子C和σ2是決定支持向量機分類性能的重要參數。為了能夠獲得更為精確的分類結果，本文選擇遺傳算法對懲罰因子C和σ2進行選擇和優化。即首先將懲罰因子C和σ2的參數形式轉化為基因編碼的表達形式，形成由200 個個體組成的種群規模，再從懲罰因子C和σ2的解空間中隨機選擇一個起點出發，利用適應度函數指導其搜索的方向，最終選取訓練準確度最高的C和σ2作為最優參數，為了提高運算速度，本文選取進化代數為20。

3.2 基于CMPE算法軌枕狀態識別

結合CMPE 算法和支持向量機，提出的軌枕狀態診斷方法流程圖如圖5所示。該方法步驟包括以下幾個方面：

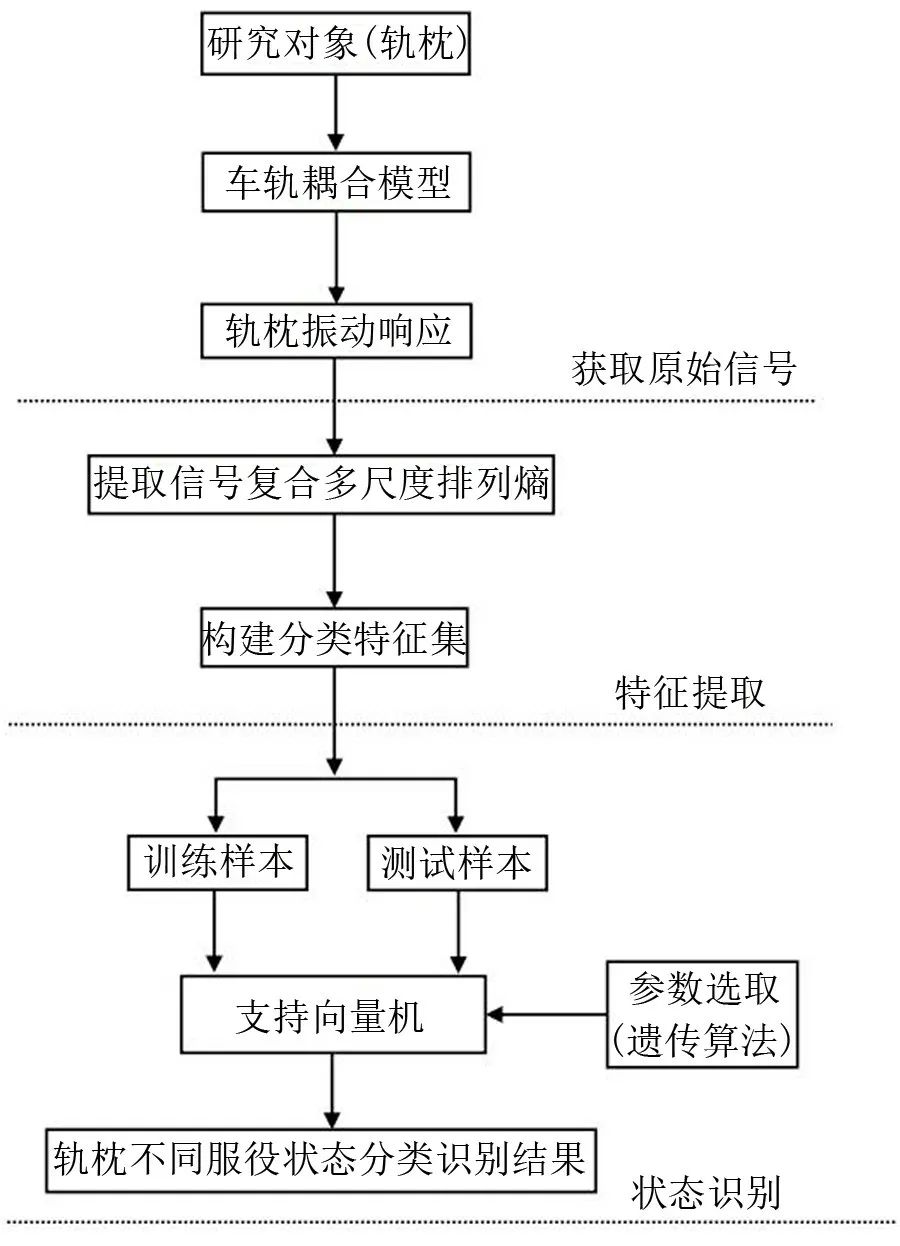
圖5 軌枕故障識別流程圖

①利用車軌耦合垂向振動模型，獲取軌枕的振動響應；

② 利用CMPE 算法，提取軌枕振動響應的CMPE值，并建立軌枕服役狀態的特征集；

③以提取的CMPE 值特征集作為支持向量機的輸入，對其進行訓練和測試，最終實現對軌枕的狀態診斷。

根據圖5所示的流程，本文對5種軌道不平順譜下，不同列車速度時的5 種軌枕振動響應進行分類識別。分別選取S1、S2、S3、S4 和S5 5 種道床結構板結情況的前90個CMPE值作為訓練集，剩余的10個CMPE 值作為測試集，具體的數據描述如表2所示。

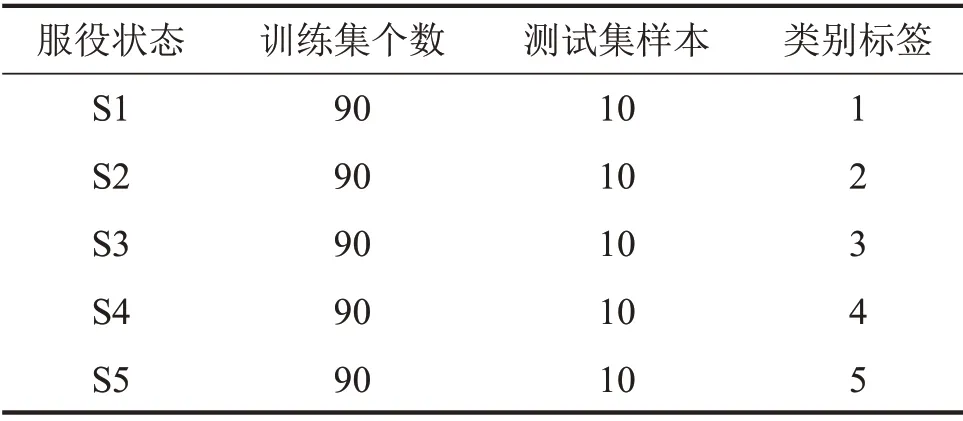
表2 不同軌道不平順譜的各列車速度下的實驗數據描述

根據上述方法，以各軌道譜激勵下，列車速度200 km/h 時的軌枕振動響應為例，利用支持向量機對輸入的CMPE 特征集進行訓練和識別，得出的分類結果如圖6所示。

用同樣的方法對各軌道譜激勵下，列車速度200 km/h時的軌枕振動響應的MPE值進行訓練，得到的識別準確率如圖7所示。

對比圖6 和圖7 可以發現，相同列車速度下，基于CMPE的錯分個數要比基于MPE的錯分個數少，識別效果更好，這證明了基于CMPE 的軌枕振動響應診斷方法的優越性。

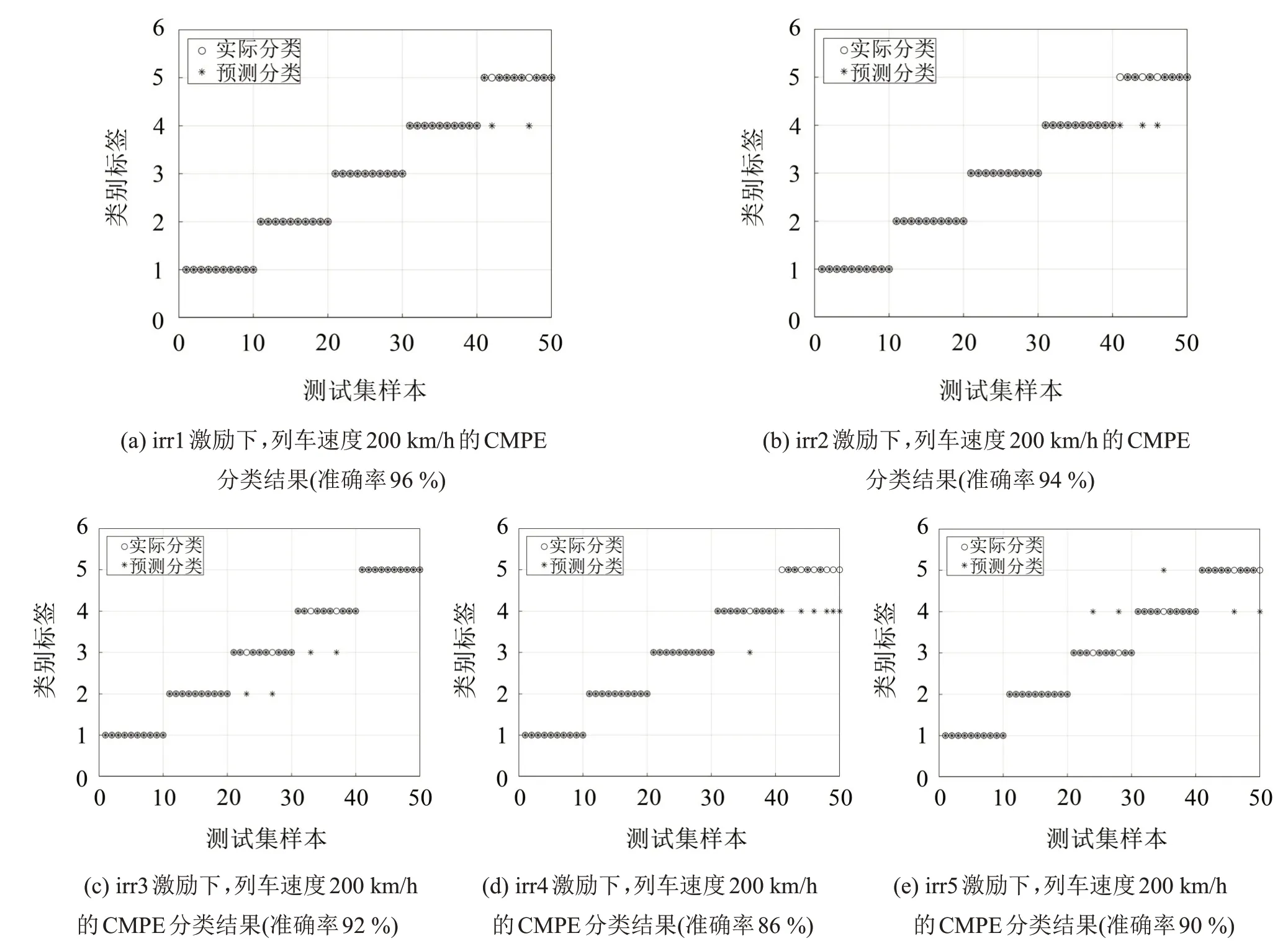
圖6 列車速度200 km/h的CMPE分類結果

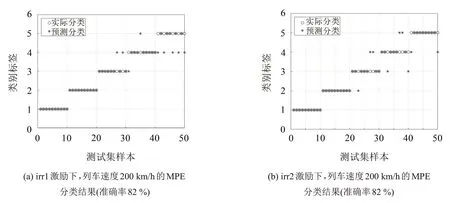
圖7 列車速度200 km/h的MPE分類結果

圖7 列車速度200 km/h的MPE分類結果

為使得基于CMPE的軌枕狀態識別方法更具說服力，本文分別對5種軌道不平順譜下，各列車速度時的5種道床結構板結情況時的軌枕振動響應進行了分類識別，識別準確率如表3所示。

根據表3 可以看出，基于CMPE 的軌枕服役狀態診斷方法，識別準確率可以達到90%以上，可以得到較為理想的診斷效果，充分證明了基于CMPE和支持向量機的方法在軌枕狀態識別上的有效性，這表明以上所提出的軌枕狀態診斷方法在工程上具有較高的應用價值。

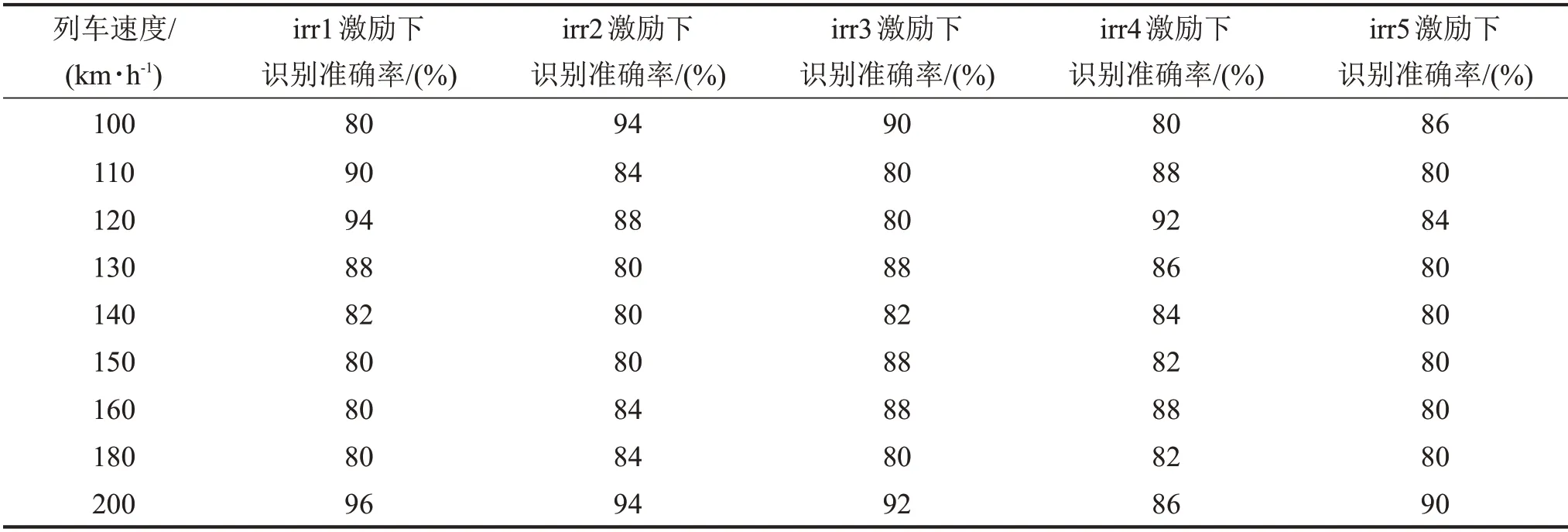
表3 不同軌道不平順譜激勵的各列車速度下的分類準確率

4 結語

本文提出了一種基于CMPE的軌枕狀態診斷方法，通過與其他方法進行比較，得出了以下結論：

(1) 利用CMPE 算法提取了軌枕振動響應的CMPE值，大大降低了原始數據的維度，為后續算法的運行節約了時間。并且CMPE 算法較MPE 算法更具有穩定性，對時間序列的長度依賴度低，能夠保留各個尺度上蘊含的豐富信息。

(2)對比了CMPE 值構成的特征集和MPE 值構成的特征集分別作為分類算法的輸入的識別準確率，發現CMPE 特征集作為輸入的識別準確要明顯高于MPE特征集，進一步證明了CMPE算法較MPE算法的優越性。

(3)以CMPE 值構成的特征集為分類算法的輸入，利用遺傳算法優化的支持向量機對軌枕不同服役狀態進行識別分類，最終的識別準確率能夠達到90%以上，出現誤檢的情況很少,實現了對軌枕不同服役狀態的識別和診斷，證明了本文所提方法的優越性。