基于能量分析法對阻尼鋼板聲輻射的優化研究

劉杰昌，常光寶，李書陽，鄢 亮

（1.上汽通用五菱汽車股份有限公司，廣西 柳州545007；2.上海桓領信息科技有限公司，上海201101）

隨著社會的不斷發展，在汽車、飛機、鐵路運輸和船舶行業內振動和噪聲問題受到越來越多的關注[1]。當前被動振動和噪聲控制應用非常廣泛，其中阻尼衰減技術[2-3]，由于其結構簡單、低成本、方便布置等優點，得到了廣泛的工程應用。通常根據阻尼材料鋪設的形式分為自由阻尼（Free Layer Damping，FLD）和約束阻尼（Constrained Layer Damping，CLD）結構。

自由阻尼結構就是將阻尼材料貼附在鋼板上形成的結構[4]。而約束阻尼結構像三明治一樣，兩側部分為鋼結構，中間部分為阻尼層[5]。它們的振動衰減機理一樣，都是隨著鋼板的振動而發生變形，并將獲取得到的動能轉換成熱能，進行能量的耗散，實現振動的衰減。

目前，對阻尼鋼板結構優化的研究有許多[6-7]，主要是根據結構的力學特性，確定阻尼材料的最優布局。楊德慶等[8-9]提出了阻尼胞單元和阻尼拓撲敏度等概念，建立了基于阻尼拓撲敏度綜合評價的阻尼材料拓撲優化準則，并用于頻率和動響應約束下自由阻尼層結構阻尼材料的配置優化；徐偉等[10]鄭玲等[11]根據經典薄板理論，建立約束阻尼鋼板的有限元模型，推導出其輻射聲功率及靈敏度公式。以聲功率最小的優化目標，采用漸進式優化算法，得到約束阻尼材料的最優優化結構。王超等[12]設計了兩種典型的阻尼薄板復合結構，在3種邊界條件下，阻尼薄板復合結構的振動特性，從模態應變能角度分析了復合結構的阻尼損耗因子的精度，對降低結構振動，改善輻射噪聲有著較為重要的工程應用意義。

在汽車領域由于自由阻尼結構簡單、制作工藝方便、成本低等優勢有著廣泛的應用。在該背景下，本文研究一塊鋪滿阻尼材料的鋼板，在考慮真實的激勵輸入的情況下，采用漸進式優化算法以阻尼材料的體積分數為約束條件進行仿真計算，得到阻尼鋼板輻射聲場中目標區域的聲功率能量，將不同位置對應的聲功率能量值映射到阻尼鋼板上，最終得到該阻尼鋼板的敏感度分布云圖，并采用仿真和試驗進行驗證優化結果。本方法從聲功率角度出發，為結構噪聲設計提供了一種重要的技術手段。

1 阻尼鋼板仿真建模及優化

1.1 離散系統振動微分方程介紹

對自由阻尼鋼板，其主要分析環節為阻尼材料對阻尼鋼板的振動性能的影響，在建模過程中，需要對阻尼材料的阻尼效果進行準確的建模；對于結構件來說，采用有限元分析理論，將結構等效為多自由度系統進行簡化，并采用多自由度系統的強迫振動方程進行描述，如式（1）所示；

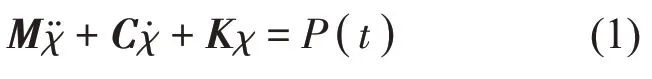
其中：M為質量矩陣，C為阻尼矩陣，K為剛度矩陣，P(t)為施加載荷。

對于黏彈性阻尼材料，其阻尼特性可以簡化為線性阻尼，因此在其阻尼參數處理的過程中，將采用線性等效的質量矩陣及剛度矩陣進行簡化，因此對于阻尼材料本身，其將采用復模量及密度進行參數表征。

根據離散系統振動微分方程，將黏彈性阻尼材料采用線性多自由度系統方程進行簡化，最終對黏彈性阻尼材料的參數表征體現為復模量及其密度；而采用國標GB 18258[13]中提到的結構損耗因子η對阻尼材料的阻尼性能進行表征，其與阻尼材料的復模量之間的關系式（2）所示：

式中：Ei表示為耗能模量；Er表示為儲能模量。因此，阻尼材料的復模量可以與結構損耗因子進行相互轉換，從而作為結構有限元分析及建模的輸入。

1.2 阻尼板聲輻射計算

將平板表面離散成N個面積相等的小單元，每個單元面積為Δs。由于每個單元面積都很小，假設每個單元內的速度處處相等，這樣就可以利用單元內某一點的振動速度代表整個小單元的振動速度。

平板輻射聲場[14]內某點a的輻射聲壓可以表示為：

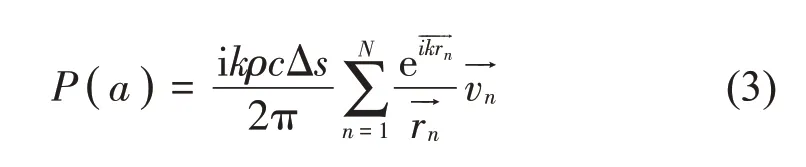
式中：P(a)表示場點a處的聲壓；i=；ρ表示空氣密度；c表示聲波在空氣中的傳播速度；k表示波數表示聲壓頻率表示聲源上某點n到場點位置a的位移矢量表示聲源表面法向的振速矢量。

2 阻尼鋼板聲輻射仿真及優化

考慮到乘用車的應用背景，同時避免環境噪聲對阻尼鋼板優化結果的干擾，故建立一個類似車廂式封閉的箱體進行阻尼仿真分析，如圖1（a）所示。

采用Nastran 和Actran 軟件進行聯合仿真進行優化分析，Nastran軟件分別對結構和聲腔進行模態計算，然后在Actran中讀取模態結果，搭建模態疊加法的仿真模型。基于Python語言編程對Actran進行優化仿真計算。

2.1 阻尼板箱體模型

在Actran中建立邊長為1 m的立方體有限元網格模型，其中把箱體金屬外殼看作為殼單元，厚度為2 mm，材料為#304 不銹鋼。箱體內部含有吸聲棉，并通過駐波管對吸聲棉進行吸聲系數進行測試，獲取吸聲棉的聲學參數。其中阻尼鋼板如圖1（b）所示，其中采用半功率帶寬法[13]對阻尼材料進行測試，獲取阻尼材料參數。

在Actran 中建立有限元仿真模型，如圖1（a）所示，在箱體阻尼鋼板的外表面上一點，輸入0～500 Hz的白噪聲激勵，在箱體內幾何中心處布置一個麥克風監測點。

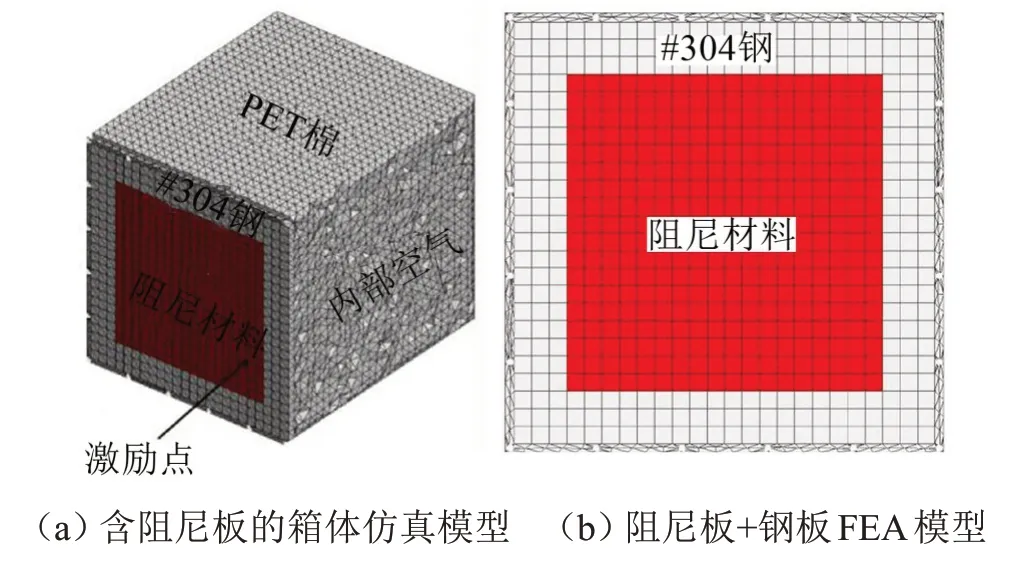
圖1 阻尼板聲輻射FEA模型

2.2 阻尼板仿真分析優化

阻尼板的仿真優化是在Actran 軟件基礎上，采用Python 語言進行二次開發的的一個過程，具體的優化技術路線如圖2所示。

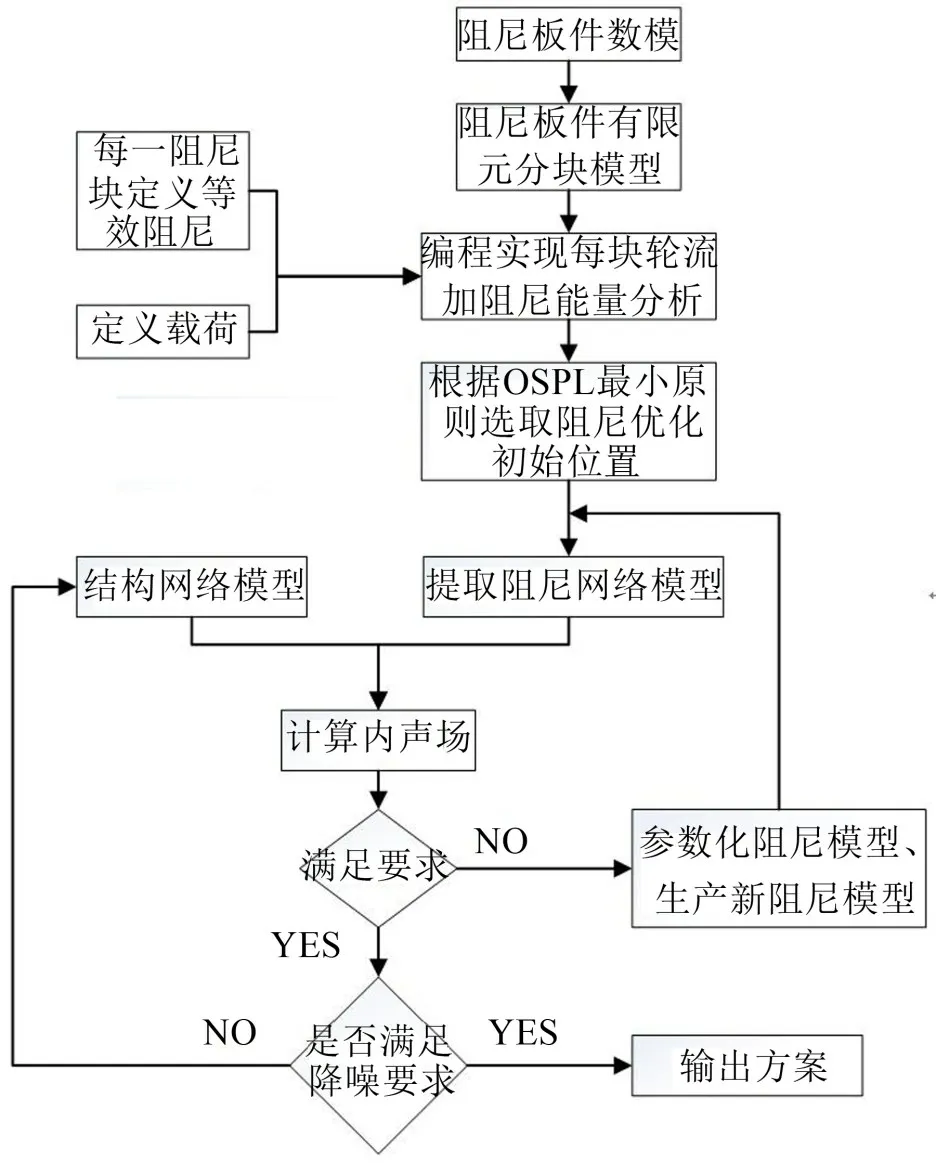
圖2 阻尼板優化技術路線

首先對阻尼鋼板有限元網格模型進行分塊，對應軟件中每一個塊內的網格數量。本文按9個單元為一塊進行劃分，規定每一塊阻尼稱胞元，共計64個胞元，并進行編號，如圖3（a）所示。然后通過編程控制，輪流給每個胞元定義一個等效阻尼系數0.4。然后在箱體外側施加0～500 Hz 的白噪聲激勵，步長為1 Hz，進行聲功率能量計算，則箱體內的麥克風監測點得到不同胞元所得到的響應結果。

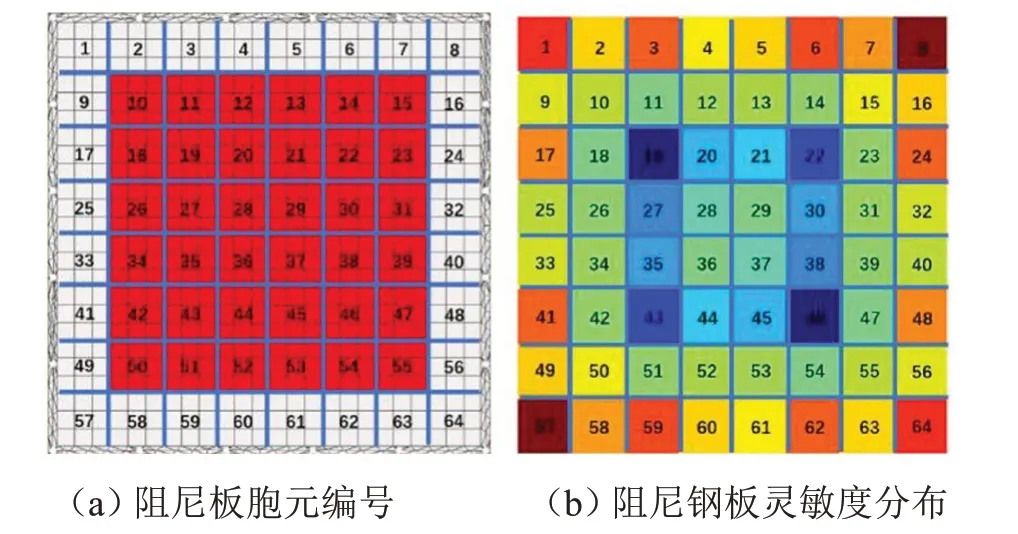
圖3 阻尼板模型

最后將這些結果映射到對應的胞元上，形成阻尼鋼板靈敏度云圖分布，如圖3（b）所示。其中顏色越淺表明越敏感。根據全局聲壓級（Overall Sound Pressure Level，OSPL）最小的原則，將64個胞元對應的能量結果，按從小到大進行排序。在質量不變的前提下，選擇全局優化函數，參數化阻尼單元，并約束全局聲壓級小于原設計，且阻尼材料厚度為均勻分布，設定最大迭代次數，優化目標為降噪，在優化計算過程中，不同數量的胞元，就有相應的厚度。

其中當胞元數量為25，阻尼厚度為4.32 mm，阻尼材料的位置分布如圖4所示。該種布局達到很好的降噪效果。

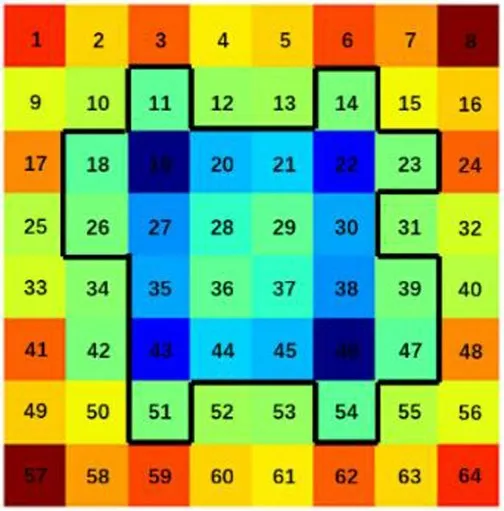
圖4 優化后阻尼模型

在Actran 軟件中建立仿真模型，同時考慮聲振耦合效應，對優化的阻尼模型進行噪聲響應仿真分析，阻尼仿真模型如圖5所示。

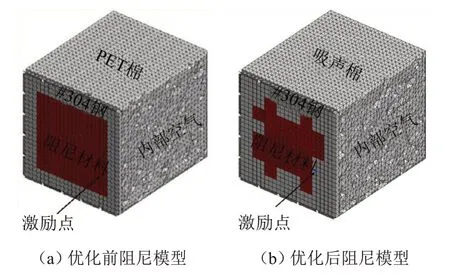
圖5 Actran仿真模型

建立優化前阻尼模型仿真箱體和優化后阻尼模型仿真箱體，在激勵點輸入試驗測得的0～500 Hz的白噪聲信號，建立聲振耦合邊界設置，進行模態疊加法仿真分析，在箱體內部的同一坐標設置為麥克風監測點。通過計算，含優化前阻尼模型箱體內麥克風監測點處的全局聲壓級為98.80 dB，含優化后阻尼模型箱體內麥克風監測點處全局聲壓級為96.70 dB。采用能量分析法對阻尼鋼板進行優化，實現了2.10 dB的降噪效果，如圖6所示。

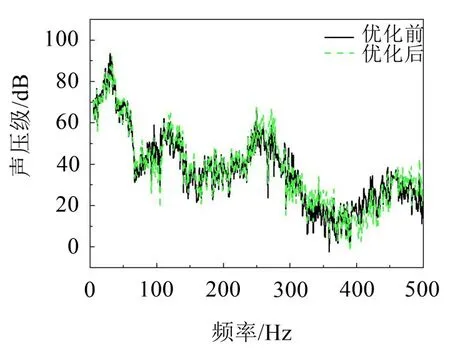
圖6 優化前與優化后聲壓級對比

3 阻尼箱體試驗驗證

3.1 阻尼噪聲測試臺介紹

按照仿真優化后的阻尼鋼板尺寸，制作一張阻尼鋼板，如圖7（a）所示。同時，阻尼鋼板箱體的噪聲試驗平臺和仿真模型一樣，其中包含阻尼鋼板、304不銹鋼金屬外殼和吸聲棉等部分，阻尼鋼板與箱體之間的連接采用密封膠泥進行減振和密封處理，并采用螺栓固定連接，如圖7（b）所示。

圖7 阻尼板輻射噪聲測

在信號發生器內定義信號輸入，使激振器產生頻段為0～500 Hz的白噪聲，作用在阻尼鋼板上，同時通過力傳感器進行采集激勵信號。在箱體的幾何中心布置一個麥克風傳感器，使用LMS數據采集儀進行聲輻射信號的采集。

3.2 仿真和試驗數據驗證

通過上述試驗，力傳感器得到激勵輸入的頻譜信號，考慮上文做阻尼材料布置優化的激勵輸的頻譜信號與本次試驗的信號有一定差異，所以在仿真中更換為本次試驗中測得的激勵輸入信號作為新的激勵輸入，并進行仿真計算。最后將仿真得到的阻尼鋼板聲輻射頻譜信號和試驗得到的阻尼鋼板聲輻射頻譜信號進行對比，如圖8所示。

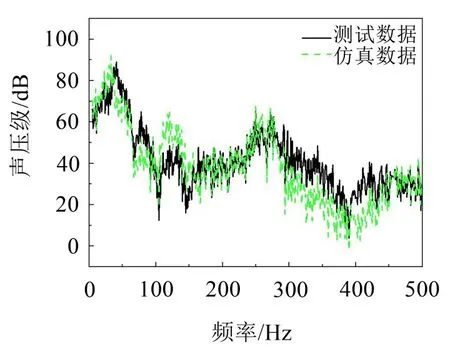
圖8 仿真與測試結果對比

對試驗中麥克風傳感器測量的時域數據進行傅里葉變換，不采用倍頻程合成，而是計算0～500 Hz頻域內的全局聲壓級為95.82 dB，仿真得到的麥克風測點的全局聲壓級為96.70 dB，誤差為0.88 dB。從圖中也可以看出仿真和測試有著較好的一致性。

4 結語

本文采用能量分析法對阻尼鋼板聲輻射的優化，在不改變質量的情況下，對阻尼材料分布區域進行合理優化，實現降低聲輻射的優化目標。并且本文中的優化方法，是基于Actran軟件的二次開發，為工程應用提供一種重要的手段。

(1)基于Actran軟件進行二次開發，對阻尼板進行分塊，并使用漸進優化算法逐步計算每小塊的振動靈敏度，進而得到一種優化模型。

(2)基于優化后的模型，編程對厚度曲行參數優化，控制阻尼單元模型的生成，并約束聲輻射小于原設計，優化目標為降噪，從而達到降噪的效果，此過程可以找出合理厚度。

(3)根據優化算法得到的優化模型，進行試驗驗證，通過試驗和仿真數據的對比，確認了仿真的精度以及優化方法的合理性，為阻尼優化在工程的應用提供了一種重要的技術手段。