論數形結合思想在初中數學勾股定理教學中的滲透與應用

賀洪秋

摘 要：數形結合是初中生必須要掌握的一項學習技能。掌握科學有效的解題方法，才能夠應用到實際問題中。勾股定理是初等幾何的重要定理，是數字與圖形相互轉換的生動例子。結合實際舉例對勾股定理的數形結合進行論證。

關鍵詞：初中數學;數形結合;勾股定理

數學概念對初中生而言有較高的難度，具備抽象性和概括性的特點，因此想讓初中生更好地了解注重數學的內在邏輯，我們應該轉化為具體的、可見的圖形幫助初中生來學習，將抽象的數學語言轉化為生動直觀的圖形，從而幫助學生更好地學習和掌握學習數學的方法。本文主要以數形結合思想在勾股定理教學的應用，從導入新課、講授新課、新課小結、作業等方面展開討論。

一、在課前導入中滲入數形結合思想

導入是吸引學生興趣的切入點，是課堂的重要一步。在學習勾股定理前，以生活圖片導入，學習的內容來自生活，從而增強學生對數學學習的興趣。導入使用的圖片是2002年被譽為“數學奧運會”的會徽，也是我們課本的封皮上的風車圖片，第一個疑問，通過這個圖片大家能看出一些什么內涵。通過設疑，引起學生的好奇心，提高學生的學習興趣。

二、講授新課時滲透數形結合

通過圖片導入激發學生的學習興趣，然后也讓學生自己參與到課堂當中，發現問題并解決問題，也增加了學生對學習數學的興趣，也更體現了學生的主體地位。我們從等腰直角三角形得出，斜邊的平方等于兩個直角邊的平方和。那么直角三角形是不是也可以得出這個結論呢？我們繼續探討學習。我們可以在網格內隨意畫出一個直角三角形，并作圖以三角形的三條邊延伸出三個正方形。我們首先還是把形轉化為數，分別求出三個正方形的面積，從而來判斷三角形三邊的關系。從個性到共性，從特殊到一般，不僅是數形結合思想的深入，也會使學生的遷移能力和邏輯思維能力得到提升。

三、數形結合思想在初中數學勾股定理教學中的實例分析應用

一根竹竿由于受大風影響從中部折斷，已知切斷點到地面的垂直距離是9米。倒落在地的竹竿頂部到竹竿根部的距離是12米，那么這根竹竿的長度是多少米？這道題目，如果學生能夠從把文字轉換成圖形，那么大家得出的這個結論就會非常快，這個就是文字與圖形的轉換的學習能力的體現。我們可以畫出圖，整個的一根竹子，從某一個節點倒下以后，也就是會產生一個斜線，那么在地面的這是一條直線，其實整體就是一個直角三角形。切斷點到地面的距離，也就是從折斷點到竹竿底部的長度是9米，頂部到竹竿底部距就是平面上的距離，是12米。事實上所組成的這個三角形的斜線就是竹子的折斷點以上的高度，那么我們在做這道題的時候，運用勾股定理求出斜方的長度，加上切斷點到地面的垂直高度9米，就是我們整個竹竿的高度。

四、課堂小結與作業練習

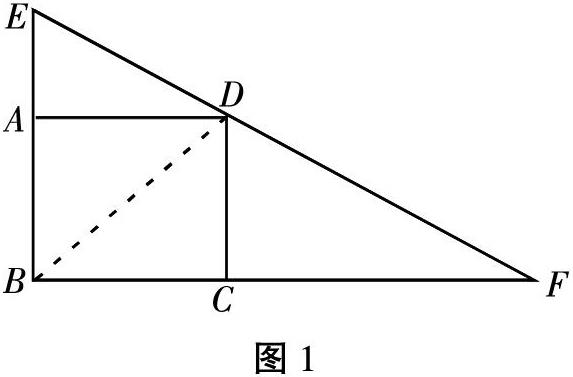
得出結論，直角三角形斜邊的平方等于兩個直角邊的平方和。實踐是檢驗真理的唯一標準，我們應該再舉出一些實例，幫助學生來運用勾股定理。例題如圖1所示，從正方形ABCD的頂點D延伸出一條直線，交BC、BA的延長線于F、E點。求證：BE+BF大于等于4BC。從本道題目來看，具備一定的難度，首先大家應該根據題目畫出相應的圖畫，出圖以后我們發現，僅僅用圖形并不能夠完成這道題目，因此，要將圖題中的圖形轉化為數字來進行求證。

第一步，整理問題BE+BF=BA+AE+BC+CF=2BC+AE+CF，即得AE+CF大于等于2BC。第二步，在圖形問題遇到一定難度時候，我們可以轉化為數字，在這個時候可以設AE的長度為a，CF的長度為b，BC的長度為m。即可轉換為a+b大于等于2m。第三步，連接BD，我們可以看到三角形BEF的面積=三角形BED面積+三角形BDF的面積。因此我們可以得出，最后化簡為m2=a×b。則帶入步驟2，得出a+b大于等于2m成立。即問題得證明。

五、結語

綜上所述，數形結合思想能夠幫助我們解決許多實際問題。教師要在課堂的導入環節、授課環節、作業環節都滲入數形結合這一思想，從而提高學生學習數學的綜合能力。勾股定理是數形轉化的典型代表，從這里開始學習數形結合，可以讓學生更好、更直觀地接受此思想，學生也能夠在此基礎上獲得寶貴的數學資源，積累豐富的數學思路。數形結合可以使數學問題由復雜變為簡單，由抽象變為具體，會使數學成為學生喜愛的學科。