一元二次函數、方程和不等式常見典型考題賞析
■張普懷
本章的主要解題類型有兩個方面:一是一元二次方程與一元二次不等式的基本解法,二是利用一元二次函數的性質求解有關一元二次方程與一元二次不等式問題。下面就一元二次函數、方程和不等式問題的常見典型考題舉例分析,供大家學習與提高。
題型一:三個“二次”的關系
已知一元二次不等式的解集,可知a的符號和方程ax2+bx+c=0 的兩實根,由根與系數的關系可知a,b,c之間的關系。
例1已知不等式ax2-bx+2<0的解集為{x|1 解:由一元二次不等式的解集,可知a的符號和方程ax2-bx+2=0的兩根,利用根與系數的關系可求a,b的值。 (方法1)由題設條件知a>0,且1,2 是方程ax2-bx+2=0的兩實根。 (方法2)根據題設條件,可把x=1,x=2 分別代入方程ax2-bx+2=0,可得 跟蹤訓練1:若不等式ax2+bx+c≤0的解集為{x|x≤-3 或x≥4},求不等式bx2+2ax-c-3b≥0的解集。 提示:因為不等式ax2+bx+c≤0的解集為{x|x≤-3 或x≥4},所以a<0,且-3,4是方程ax2+bx+c=0的兩根。由根與系數的關系可得解得 所以不等式bx2+2ax-c-3b≥0可化為-ax2+2ax+15a≥0(a<0),即x2-2x-15≥0。由此解得x≤-3或x≥5,故所求不等式的解集為{x|x≤-3或x≥5}。 必須是具有相同性質,可以比較大小的兩個量才可用不等式來表示,沒有可比性的兩個量之間不能用不等式來表示;在用不等式表示實際問題時,一定要注意單位的統一。 例2某商人如果將進貨單價為8元的商品按每件10 元銷售,每天可銷售100 件,現在他采用提高售價,減少進貨量的辦法增加利潤。已知這種商品的售價每提高1 元,銷售量就相應減少10 件。若把提價后商品的售價設為x元,怎樣用不等式表示每天的利潤不低于300元? 解:由“這種商品的售價每提高1 元,銷售量就相應減少10件”確定售價變化時相應每天的利潤,由“每天的利潤不低于300 元”確定不等關系,即可列出不等式。 若提價后商品的售價為x元,則銷售量減少×10=(x-10)×10(件),因此,每天的利潤為(x-8)[100-10(x-10)](元),則“每天的利潤不低于300 元”可以用不等式表示為(x-8)[100-10(x-10)]≥300。 跟蹤訓練2:用一段長為30m 的籬笆圍成一個一邊靠墻的矩形菜園,墻長18m,要求菜園的面積不小于110m2,靠墻的一邊長為xm,試用不等式表示其中的不等關系。 提示:由于矩形菜園靠墻的一邊長為xm,而墻長為18m,所以0 解決此類問題一定要在理解的基礎上,熟記不等式的性質并注意在解題中靈活應用。應用不等式的性質進行推導時,要緊扣不等式性質的成立條件,且不可省略條件或跳步推導,更不能隨意構造性質與法則。 幾個重要的不等式(下面不等式等號成立的條件均為a=b):a2+b2≥2ab(a,b∈≥2(a,b同號);ab≤b∈R);。算術平均數與幾何平均數:設a>0,b>0,則a,b的算術平均數為,幾何平均數為,基本不等式可敘述為兩個正數的算術平均數不小于它們的幾何平均數。利用基本不等式求最值問題:已知x>0,y>0,如果積xy是定值p,那么當且僅當x=y時,x+y有最小值(積定和最小);如果和x+y是定值p,那么當且僅當x=y時,xy有最大值(和定積最大)。 例4已知正數x,y滿足x+2y=3,則的最小值為_____。 不等式ax2+bx+c>0對任意x∈R 恒成立?不等式ax2+bx+c<0對任意x∈R恒成立?。 例5關于x的不等式(a2-1)x2-(a-1)x-1<0的解集為R,求實數a的取值范圍。 解:由a2-1=0,可得a=±1。當a=1時,不等式可化為-1<0,解集為R;當a=-1時,不等式可化為2x-1<0,解集為,此時解集不為R。所以a=1,滿足條件。 由a2-1≠0,可得a≠±1。原不等式解集為R 的條件是: 跟蹤訓練5:若不等式(a-2)x2+2(a-2)x-4<0對一切x∈R 恒成立,則a的取值范圍是____。 提示:當a-2=0,即a=2時,不等式為-4<0,顯然恒成立,這時解集為R,可知a=2滿足條件;當a-2≠0時,要使原不等式解集為R,需滿足解得-2 綜上所述,a的取值范圍是-2 a≥y或a≤y型不等式是恒成立問題中最基本的類型,a≥y在x∈D上恒成立,則a≥ymax(x∈D,y存在最大值);a≤y在x∈D上恒成立,則a≤ymin(x∈D,y存在最小值)。 例6已知y=x2+ax+3-a,當-2≤x≤2 時,y≥2 恒成立,求實數a的取值范圍。 跟蹤訓練6:對?x∈[1,4],不等式x2-(a+2)x+4≥-a-1恒成立,求實數a的取值范圍。 提示:當x=1 時,不等式為0≤4 恒成立,此時a∈R; 故實數a的取值范圍為(-∞,4]。 感悟與提高 1.設a,b是非零實數,若a題型二:用不等式(組)表示不等關系
題型三:利用不等式的性質證明不等式

題型四:利用基本不等式求最值

題型五:一元二次不等式在實數集上的恒成立問題
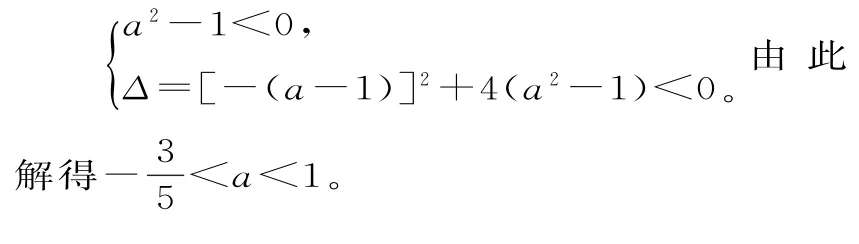
題型六:一元二次不等式在某特定范圍上的恒成立問題




