小學乘法運算的內容進階及教材編寫邏輯

劉加霞

北京教育學院初等教育學院院長，教育心理學博士，教授，教育部國培專家庫成員;提出“把握數學本質是一切教學法的根”“實證研究學生是有效教學的根本”“培訓實質是改變與創新”等觀點，以及“CARE伙伴式”校本研修模式;在《課程·教材·教法》《中國教育學刊》《中小學管理》《人民教育》《小學數學教師》《小學教學》等期刊發表論文百余篇，著作有《小學數學有效教學》《小學數學有效學習評價》《小學數學課堂教學設計》等。

小學階段運算的對象主要是自然數、分數與小數。各版本教材都是先編排自然數四則運算，不同的是分數、小數運算的編排順序：有的先學習分數運算，再學習小數運算，有的則反之。內容編排的順序不同，算法及解釋其算理的依據就不同，乘法運算教學的整體邏輯結構也就不同。

近期，筆者看到關于多位數乘法、小數與分數乘法單元教學的幾個案例，都特別強調“計數單位及其個數相乘”這一“原點”，有簡單問題復雜化之嫌。因此，我們有必要追問：作為“高級運算”的乘法，其算法算理的教學應該退回“原點”，還是利用“前階”內容通過推理獲得？小學階段所有乘法運算的內容進階及邏輯結構是什么？“退回原點”追問算理是否符合整套教材的編寫意圖？

一、乘法算理是否要退回到“計數單位及其個數相乘”

有教師讓學生以下述方式理解14×12的算法算理：“先拆后合”，即讓學生通過“列表格”（拆分為“10+4”與“10+2”相乘）解釋其乘積是2×4個“1”、2+4個“1×10=10”與1個“10×10=100”的和。這樣理解是否有必要？根據乘法意義將之拆為“14×2與14×10”是否更清楚？又如，0.2×0.3有必要按“0.2×0.3=2×0.1×3×0.1=2×3×（0.1×0.1）=6×0.01=0.06”的步驟計算嗎？分數乘法是否有必要這樣計算：[3/5×2/7=][3×1/5×2×1/7=3×2×（1/5×1/7）][=6×1/35][=6/35]。

如此而言，2×3是否也得回歸到“2×3=2×1×3×1=2×3×（1×1）=2×3×1=6”？那么，10×10=100、0.1×0.1=0.01、[1/5×1/7=1/35]等成立的理由又是什么呢？計數單位與計數單位相乘產生新計數單位的“算理”是否更讓人難以理解？

如果按照前述邏輯，教材編排就要先學習計數單位與計數單位相乘;為了解釋小數計數單位相乘，就要先學習分數乘法，再學習小數乘法;解釋“分數單位乘分數單位”就需要通過分數的意義（借助分數面積模型圖）求得結果。既然如此，我們為什么不直接借助分數的意義理解并歸納得到真分數乘真分數的計算法則呢？這不禁讓我們思考：哪個知識點作為乘法運算的邏輯起點合適？借助已經學過的概念、性質與定律等，通過推理，概括乘法運算法則是否可行？

為此，筆者梳理了小學階段自然數、分數與小數乘法運算的內容進階及其邏輯結構，研究發現：大多數教材都沒有退回運算的“原點”，而是以“前階”內容作為教學乘法算法算理的起點。

二、自然數乘法教材編排順序及對算法算理的處理

運算的學習內容包括運算的現實意義、算法算理以及運算性質、定律等。乘法的現實意義最豐富，有多種現實模型，能解決各類問題，其內容編排順序為：二年級初步認識乘法，包括乘法的等量組聚集模型、實物或點子圖矩形模型;三年級學習乘法的倍數模型、配對模型以及長方形面積的矩形模型;四年級學習乘法的“速度—時間”模型、“單價—數量”模型;五、六年級學習乘法的“工效—工時”模型以及正比例關系等。自然數乘法的內容都安排在二至四年級，其學習進階及邏輯結構基本相同。

階段1：二年級（上）“乘法口訣”。根據乘法意義探究發現“口訣”，通過口訣快速得到一位數乘一位數的積，其算理強調乘法意義——幾個幾的和，或者理解為以某個因數為“單位”，強調單位的個數，而不是回歸到計數單位“一”“十”的個數。

階段2：三年級（上）“一位數乘整十、整百、整千等數”。根據乘法意義，通過探究發現規律，得出口算法則——先轉化為乘法口訣，再看因數中有幾個“0”，積的末尾就添加幾個“0”。有的教材將其安排為1課時內容，有的則與“兩位數乘一位數不進位口算”合并作為1課時，但都沒有強調必須學習10×10、100×100等算式。

階段3：三年級（上）多位數乘一位數、0乘任何數。以“兩位數乘一位數”的筆算為主，研究其算法算理，然后遷移至多位數乘一位數。不同版本教材的處理方式不同：有的只介紹豎式筆算并解釋豎式中每一步的算理;有的則介紹多種算法，例如轉化為加法計算、借助矩形點子圖計算、轉化為乘法口訣和整十數乘一位數計算，然后介紹乘法豎式。

階段4：三年級（下）“因數末尾有0的口算乘法”。有的教材先研究一位數、兩位數乘10的口算法則，再探究兩個因數末尾都有0的乘法口算法則;有的教材通過探究幾組“有特點”的乘法算式的規律，發現因數末尾有0的乘法口算法則。例如，計算3×2、3×20、30×20;12×4、12×40、120×40。所有版本教材都沒有特別處理自然數計數單位乘計數單位的口算。

階段5：三年級（下）“兩位數乘兩位數”。這個內容是筆算乘法的關鍵，不同版本教材的編寫差異較大。有的教材直接介紹豎式算法，能夠借助數的意義以及整十數乘兩位數理解“第二個部分積”的算理即可。而有的教材與學習兩位數乘一位數一樣，介紹多種算法，并把“表格法”作為新知識學習。筆者更贊同前者的處理。要求學生將直觀點子圖、表格法以及豎式的每一步計算之間都建立相應聯系的做法超出了課程標準的要求。

階段6：四年級“三位數乘兩位數”。課程標準只要求“能計算三位數乘兩位數”，不要求計算其他更多位數的乘法。

可以看出，第1階段、第2階段是基礎，第3階段、第4階段是關鍵，前4個階段內容構成了乘法計算的核心，其他多位數相乘都是根據數的意義（組成與分解）以及乘法分配律轉化為這4項內容。因此乘法計算的根本是口訣，該口算的口算，該筆算的筆算，能借助“前階”內容解釋“后階”的算理即可，不需要也不適合追根到“計數單位及其個數相乘”。

三、分數、小數乘法教材編排順序及對算法算理的處理

不同版本教材對于分數、小數乘法的編排順序（學習進階）不同。大陸各版本教材都是先學習小數乘法、再學習分數乘法，而臺灣的翰林版、南一版教材則是先學習分數乘法、再學習小數乘法。臺灣教材解釋小數乘法的算法與算理是將小數乘法轉化為分數乘法。

所有版本教材中分數乘法的內容進階及其算法算理都相同：先學習“分數乘整數”（緊扣乘法意義、分數意義得到計算結果并歸納計算法則），再學習“分數乘分數”（根據分數意義，借助分數的“面積模型”得到分數乘分數的結果，并歸納計算法則）。沒有任何版本教材用上文第一部分提到的方法計算分數乘分數。

不同版本教材對小數乘法算法算理的內容編排不完全相同，下面具體分析。

1.大陸教材小數乘法的內容編排及算法算理

人教版、北師大版、河北版等大多數教材都是按照小數乘整數、小數乘小數的順序編排，其算法與算理也基本相同：①依據小數的現實意義將其轉化為自然數（例如2.5元=25角），按照自然數乘法法則求積，再根據現實意義確定積的小數位數;②通過將小數乘10、100等轉化為自然數，按照自然數乘法法則求積，再根據“積的變化規律”確定積的小數位數。在此基礎上，歸納得到小數乘法法則：轉化為自然數乘法進行計算后，再確定積的小數位數。

蘇教版教材對于小數乘整數的處理方式略有不同，緊扣小數意義計算，例如2.35×3（列豎式計算）是235個0.01乘3，積是705個0.01，就是7.05。這與臺灣教材對算法算理的處理相同。

2.臺灣翰林版小數乘法的內容編排及算法算理

臺灣翰林版教材仍然區分乘數、被乘數，因而小數乘法的編排較為“復雜”，其內容進階分三個階段。一是小數乘整數。四年級下學期學習一位小數、兩位小數乘整數，五年級下學期學習三位小數乘整數。二是整數乘小數。五年級下學期學習整數乘一位、兩位小數。三是小數乘小數。在五年級下學期學習，分為一位小數乘一位小數、兩位小數乘一位小數、兩位小數乘兩位小數。

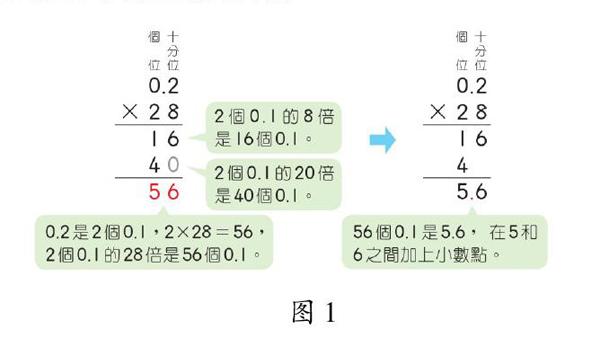
小數乘整數的算法算理是乘法的倍數含義和小數含義，如圖1某例題所示。四年級沒有總結小數乘整數的計算規律和法則，五年級下學期通過對比35×5和35×0.5的豎式計算過程總結：“整數乘以小數和整數乘法的算法很像，但要注意積的小數位數和乘數的小數位數相同。”

為了探究、歸納小數乘小數的運算法則，這版教材一共編排了6道例題和9道習題。無論幾位小數相乘其算法算理都一樣：首先轉化為分數乘法計算得出結果，探究發現計算規律與法則，再通過練習驗證與鞏固計算法則。例如，教材引導學生將0.1×0.1、1.2×0.7分別轉化成分母為十、百的分數乘分數計算后，讓學生觀察0.1×0.1=0.01和1.2×0.7=0.84兩個算式，探究兩個因數的小數位數與積的小數位數之間的關系（相同），再做3道類似的豎式計算題來檢驗和鞏固這個發現。

3.對不同版本教材小數乘法編排邏輯的總結

小數乘整數、小數乘小數的算法算理主要有三類：根據小數的現實含義及乘法意義將小數乘法轉化為整數乘法，再根據積的現實意義確定小數點的位置;根據小數意義及乘法意義將小數乘法轉化為自然數乘法，再根據積的大小確定小數點的位置;利用“積的變化規律”將小數乘法轉化為自然數乘法，再將積縮小相應倍數確定小數點的位置。

筆者所查閱的各版本教材，只有臺灣南一版教材在解釋小數乘小數算理時用到如“0.2×0.3=2×0.1×3×0.1=2×3×（0.1×0.1）=6×0.01=0.06”這樣的方法，如圖2所示。

筆者認為，教材內容的整體編排順序決定著我們如何解釋算理。該教材在豎式中用小數意義、小數計數單位乘小數計數單位來解釋算理，學生很難理解。大陸各版本教材基本都是先學習“積的變化規律”，將小數乘法轉化為自然數乘法再計算，學生對此比較容易理解。

既然乘除法是比加減法“更高級”的運算，我們就可以運用已經學過的數概念、運算性質和定律等，通過推理得出計算法則。是否“退回原點”解釋道理、解決問題，我們應該辯證地看待。

責任編輯? 劉佳