基于AHP-TOPSIS法的高原礦井通風系統方案優選 *

鄧禾苗，劉 杰，張 悅，傅 鈺，周皓文

(昆明理工大學 公共安全與應急管理學院，云南 昆明 650093)

0 引言

礦井通風系統是一個由多層次、多因素、多指標構成的復雜系統，其任務是利用通風動力，向井下輸入新鮮空氣，讓工人能安全、舒適地在井下工作，保證生產安全。近年來，國內外學者結合多種理論改進了礦井通風系統評價方法，目前主要有模糊數學[1-2]、層次分析法(AHP)[3-6]、BP神經網絡法[7]、支持向量機算法[8]以及其他相關方法[9-12]。程剛等[4]結合模糊層次分析法和多目標優化決策方法，提高了評價內容的系統性。程磊等[7]采用人工神經網絡中的BP網絡算法開發了解決非結構性問題的計算機程序，并將其應用于礦井通風系統評價。張儉讓等[8]根據支持向量機算法和通風系統的特點，通過分析具體數據，提高了計算效率，得出了評價等級。朱傳杰等[9]結合粗糙集與模糊神經網絡方法，建立了具有較高精度的通風系統評價模型。上述方法在礦井通風領域都已有一定的應用，但這些評價模型存在一些制約因素，如：評價指標不夠完整、算法精度不夠、計算過程復雜、數據處理量大等，因此這些方法在算法精度和指標選取上還有待提升和完善。此外，高原地區礦井通風系統存在許多不同于平原地區的影響因素，如：空氣稀薄缺氧、氣候變化劇烈、自然風壓不穩等。

鑒于此，在前人研究的基礎上，考慮自然風壓對通風系統的影響程度與高原地區作業場所含氧量合格率這兩個指標，基于AHP法和逼近理想解排序法(TOPSIS)構建高原礦井掘進面通風系統評價模型，并以實例驗證其合理性，最終確定最優的通風系統方案[13]。TOPSIS法能綜合考慮通風系統方案的多種指標因素，但對于多因素分析及權重計算困難且復雜[14]，AHP法則克服了該缺點，保證了算法的全局最優性。將該模型應用于高原礦井通風系統方案優選，可以使評判體系更加科學、全面、準確，評價結果更符合生產實際。

1 利用AHP法確定權重向量

1.1 比較標度

依據兩兩比較的標度和判斷原理，運用模糊數學理論，得出指標重要度比較標準[15](見表1)。

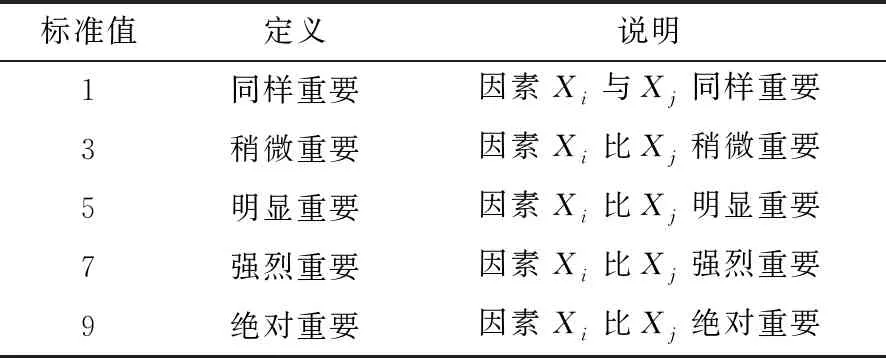
表1 指標重要度比較標準

1.2 比較判斷矩陣

設判斷矩陣為D，上一層次各因素作為下一層次指標因素的基準，兩兩比較后得

(1)

利用DW=λmaxW求解特征根問題，將得到的W歸一化后作為因素的排序權重。實際上，只能求最大特征根λmax和特征向量W的近似值。

1)判斷矩陣D各行因素的乘積

(2)

2)計算Mi的n次方根

(3)

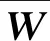
(4)

4)計算D的最大特征根λmax

(5)

以上各式中，i=1, 2,…,n。

1.3 一致性檢驗及計算權重向量

為避免單因素決策的片面性和人為主觀因素造成的誤差，需進行一致性檢驗[16]。判斷矩陣的一致性檢驗公式為

(6)

式中：n為判斷矩陣的階數，IC為一致性檢驗指標，IR為平均隨機一致性指標(見表2)。

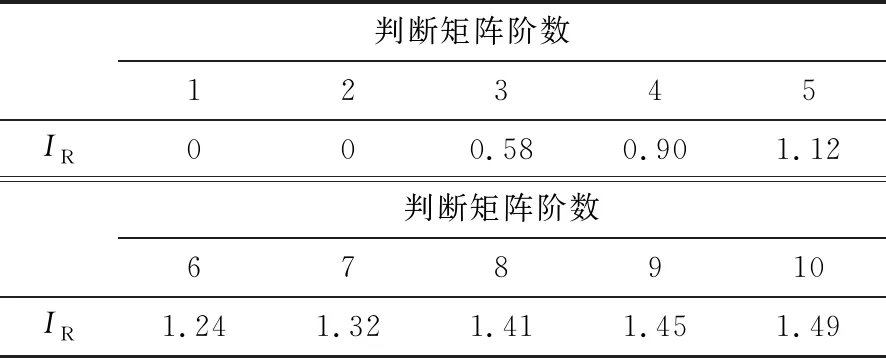
表2 平均隨機一致性指標取值

RC為判斷矩陣的一致性比例，當RC<0.1時，表示D滿足一致性檢驗要求，即可求得各層次因素的權重向量[17]。

2 構建評價模型

TOPSIS法是借助多目標決策問題中有限個評價對象與理想解的距離進行重要度排序[18]，計算出評價對象的綜合優越度，從而得出相對優劣次序。

2.1 建立初始評判矩陣

設有m個評價對象，m個方案的指標值組成方案集A={A1，A2,…，Am}；有n個評價指標，每個評判指標集X={X1，X2,…，Xn}，評判指標Xij表示第i個評價對象的第j個指標的值，其中i∈[1,m]，j∈[1,n]；則建立的初始評判矩陣為

(7)

2.2 建立標準化決策矩陣

統一指標值X的量綱后，與最優權重相乘。標準化決策矩陣B=(bij)m×n，計算公式如下：

1)效益型指標

(8)

2)成本型指標

(9)

2.3 構造加權標準化決策矩陣

將矩陣B的列向量與指標總排序權重Wn相乘，則加權標準化決策矩陣為

(10)

2.4 貼近度計算

1)確定正理想解和負理想解

C+={(maxcij∣j∈J1),(mincij∣j∈J2)}，

i=1,2,…,m;

(11)

C-={(mincij∣j∈J1),(maxcij∣j∈J2)}，

i=1,2,…,m。

(12)

式中，J1為效益型指標集，J2為成本型指標集。

2)計算評價對象與正負理想解的距離

(13)

3)確定評價對象與正理想解的貼近度

(14)

2.5 AHP-TOPSIS綜合評價模型的建立

由AHP法確定權重向量，結合TOPSIS法確定各評判對象的貼近度，建立綜合評判矩陣，得出評價對象綜合評判結果向量F[19]，表達式為

F=W×E，

(15)

式中，E為由貼近度分析形成的評價矩陣，W為由AHP法計算得到的準則層權重。

3 實例應用

3.1 高原礦井通風系統方案綜合評價指標體系

高原地區有著特殊的自然環境，海拔高、空氣中含氧量低、氣壓低。由于空氣稀薄缺氧，氣候變化劇烈，自然風壓不穩，影響了礦山正常生產[20]。因此，針對云南某礦10年規劃的3個時期的通風系統方案的優化問題，運用AHP和TOPSIS的基本理論確定其2022-2030年的通風系統優化方案，開展對高原礦井通風系統的定量、定性分析及評價。

運用AHP法基本原理，建立高原礦井通風系統方案評價指標體系(目標層)，包含3個準則層：

a.經濟指標(P1)，包括通風井巷工程費(X1)、主要通風機電費(X2)、通風機效率(X3)、通風機功率(X4)等；

b.技術指標(P2)，包括礦井風壓(X5)、礦井風量(X6)、礦井等積孔(X7)、礦井風量供需比(X8)、通風方式適用性(X9)等；

c.安全指標(P3)，包括風機運轉穩定性(X10)、用風地點風流穩定性(X11)、礦井抗災能力(X12)、自然風壓對通風系統的影響(X13)、高原地區作業場所含氧量合格率(X14)等。

領域內專家對P2、P3中的指標重要性進行了評價，并將數值量化，最高為1，最低為0。

3.2 層次結構分析

不同的判據對礦井通風系統的評價結果也不同，需要認真研究權重分配問題，將其科學量化，以使結果更加準確。最佳通風系統方案層次結構如圖1所示。各評判指標值見表3。

圖1 最佳通風系統方案層次結構

表3 各方案的評判指標值

3.3 指標權重確定

考慮3個通風系統方案評價指標的重要性程度，根據通風領域內專家的觀點和經驗，構造O-P判斷矩陣，見表4。

表4 O-P判斷矩陣

計算各指標權重，可得最大特征值λmax=3.007，IC=0.003 5,IR=0.58，RC=0.006<0.1，符合一致性檢驗要求，則權重矩陣W=[0.143,0.571,0.286]可以接受。

同理，根據評價指標重要性程度構造P1-P1j、P2-P2j、P3-P3j判斷矩陣(見表5-表7)，從而得到：

①P1-P1j矩陣：λmax=4.031，IC=0.01，IR=0.90，RC=0.011 4<0.1，W=[0.467，0.277，0.160，0.096]；

②P2-P2j矩陣：λmax=5.026，IC=0.007，IR=1.12，RC=0.006<0.1，W=[0.123，0.123，0.341，0.072，0.341]；

③P3-P3j矩陣：λmax=5.20，IC=0.005，IR=1.12，RC=0.045<0.1，W=[0.097，0.039，0.253，0.150，0.460]。

表5 P1-P1j判斷矩陣

表6 P2-P2j判斷矩陣

表7 P3-P3j判斷矩陣

各評判指標層次總排序結果見表8。

表8 層次總排序權重

分析各評價指標的最優權重，結果如圖2所示。由圖2可知：在經濟指標中，通風井巷工程費指標權重最大；在技術指標中，礦井等積孔大小和通風方式適用性尤為重要，其中通風方式適用性能保證通風系統運行的可靠性和技術合理性；在安全指標中，礦井抗災能力、高原地區作業場所含氧量合格率對高原礦井通風系統方案優選影響較大。

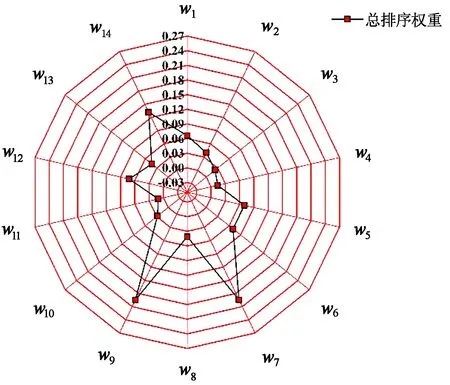
圖2 各評價指標權重分析

3.4 高原礦井通風系統方案綜合評價

3.4.1 經濟指標評價

1)根據表3構建經濟指標初始判斷矩陣

2)根據式(8)-式(10)計算加權標準化決策矩陣

3)根據式(11)-式(13)計算貼近度

在經濟指標中，通風所需的費用越小越好，屬于成本型指標，通風機效率屬于效益型指標。則正、負理想解分別為

根據式(13)，各方案與正、負理想解的距離為

根據式(14)，各方案與理想解的貼近度為

3.4.2 技術指標評價

在技術指標中，5種指標均為效益型指標，則正、負理想解為

根據式(13)，各方案與正、負理想解的距離為

根據式(14)，各方案與理想解的貼近度為

3.4.3 安全指標評價

在安全指標中，自然風壓對通風系統的影響程度屬于成本型指標，另外4個指標是效益型指標，則正、負理想解為

各通風系統方案與正、負理想解的距離為

根據式(14)，各方案與理想解的貼近度為

4 高原礦井通風系統方案綜合評價

運用AHP法確定高原礦井通風系統方案準則層權重：

W=[0.143,0.571,0.286]。

根據TOPSIS法算得的貼近度構造高原礦井通風系統方案優選評判矩陣：

根據式(15)，將W與E代入其中可得

F=W×E=(0.256 7，0.549 9，0.629 7)。

綜上可得各方案的綜合優越度為：方案Ⅰ，25.67%；方案Ⅱ，54.99%；方案Ⅲ，62.97%，即高原礦井通風系統方案的優劣次序為方案Ⅲ>方案Ⅱ>方案Ⅰ，方案Ⅲ最優。

5 結論

a.從經濟、技術和安全3個方面選取14種影響礦井通風系統方案的評價指標，運用AHP法計算各層次指標權重，得到了較為合理的評判矩陣，克服了人為主觀因素對指標權重及評價結果的影響。

b.結合TOPSIS法，建立了AHP-TOPSIS法高原礦井通風系統評價模型，計算得出3種通風系統方案的綜合優越度，分別為25.67%，54.99%，62.97%，可知方案Ⅲ最優。

c.經礦山生產實踐證明，將AHP-TOPSIS法綜合評價模型運用在高原礦井通風系統方案決策中是合理可行的。該綜合評判模型克服了單一判據的局限性與因素過多難以分配權重的弊端，為高原礦井通風系統優選方案決策提供了一種更為科學、全面、準確的方法。該模型也可應用于其他系統工程的多方案優選決策中。