基于流固耦合分析方法的固定管板換熱器流體對管束固有頻率的影響

任子奇 梁 琳 董金善 朱 雨 張森源 馮 俊

（1.南京工業大學機械與動力工程學院；2.中國特種設備檢測研究院）

流體誘導振動問題［1］是引發換熱器失效破壞的主要因素之一，而這些失效破壞往往發生在換熱管上。 因此，換熱管的振動特性和引發換熱管振動失效的機理已成為學者們的研究重點。 目前，對于有具體結構的管束振動特性的研究已經較為成熟， 可以通過多種方式去計算其固有頻率，例如GB/T 151—2014《熱交換器》附錄C中的經驗公式、TEMA標準計算方法、Macduff-Feglar計算方法、Timoshenko計算方法及Ganapathy計算方法等，通過這些計算公式可以歸納出，影響換熱管固有頻率的因素主要有換熱管直徑、 厚度、彈性模量、材料密度及幾何形狀等，然而在工程實際中還有各種可變因素制約著換熱管的固有頻率，例如折流板的尺寸、約束條件、應力、溫度、換熱管內外流體的介質屬性及換熱管內外流體對管束的影響等。 劉超鋒等通過對帶有折流板的換熱器進行系統分析，得到了影響振動的各種因素［2］。 王健分析了換熱器管束的約束條件對振動固有頻率的影響，發現增加管板厚度可以提高換熱管的固有頻率［3］。 譚蔚等通過對換熱管模型進行數值模擬，發現換熱管支撐失效可能會降低換熱管的固有頻率［4］。 呂冬祥等通過對單根換熱管進行模態分析與諧響應分析， 討論了換熱管厚度、跨距、外徑和節徑比對換熱管固有頻率的影響［5］。 任佩林等編制了換熱管固有頻率的計算程序，并驗證了該程序的可靠性［6］。蘇文獻和陳功通過使用不同的換熱管固有頻率計算方法，對比了有限元分析結果，得出了各計算方法的區別［7］。馬騰飛等使用有限元分析和試驗測試兩種方法對U型雙金屬整體螺旋翅片的振動頻率和模態進行了分析， 發現U型雙金屬復合翅片管的頻率隨著圓弧彎管段半徑R的增大而減小［8］。 范森等利用有限元分析軟件對換熱管的振動特性進行了瞬態分析、對軸向力作用下的換熱管固有頻率進行了分析，發現隨著軸向拉力的增大，換熱管固有頻率增大，拉應力的加強效應小于等效壓應力的應力軟化效應，軸向力對換熱管一階固有頻率的影響最大［9］。

在現有的標準中，影響固定管板換熱器換熱管振動的因素主要是殼程流體。 殼程流體橫掠過換熱管是引起管束振動的直接原因，殼程流體的流動對研究管束振動特性尤為重要， 而管程流體在流動過程中也會對換熱管的固有頻率造成影響。 為此，筆者通過Workbench軟件平臺， 采用流固耦合分析方法對固定管板換熱器管/殼程復雜的流場流動進行分析， 以得到管/殼程流體對管束振動特性的影響規律。

1 管束振動的機理與判據

管殼式換熱器在運行過程中，殼程流體的流動主要有縱向流動和橫向沖刷兩種狀態。 由于操作工況具有多變性、 流體流動狀態具有復雜性，流體在穩定狀態流動時對管件產生的振動、流速瞬時變化引起的振動以及內部構件在工作過程中引起的共振等這些動力機械振動，都會引起換熱管不同程度的受激振動。 其中，誘發管束振動的主要原因是橫向流誘振。 雖然，縱向流所激發的振動幅值較小，危害性較低，一般情況下可不考慮它對換熱管的損害，但當流體流經管道的流速瞬時變化較大時，縱向流激振會有較大幅值的變化，此時需考慮它對管束振動產生的影響［10］。

目前， 普遍認可的管束振動機理是卡門旋渦、紊流抖動、流體彈性不穩定和聲共振［11］。 當殼程流體出現以下任一情況時，都有可能發生管束振動，引起管束破壞，具體情況為：

其中，do為換熱管外徑。

卡門旋渦頻率的計算式如下：

式中 St——斯特羅哈數。

紊流抖振主頻率的計算式如下：

從式（1）～（4）可以看出，換熱管的固有頻率是影響管束振動的一個重要影響因素。 因此，流體對管束固有頻率影響的研究就顯得格外重要。

2 流固耦合基本理論

流固耦合主要是研究流體與固體的相互作用，并將流體作用下的固體和靜應力作用下的固體對流體的作用表現出來的一種分析方法。 在流固耦合理論使用過程中主要用到了連續性方程、動量方程和結構動力方程：

式中 ［C］——結構的阻尼矩陣，［C］∈Rnn；

{F}——結構的載荷向量，{F}∈Rn；

［K］——結構的剛度矩陣，［K］∈Rnn；

［M］——結構的質量矩陣，［M］∈Rnn；

p——流體的壓強，MPa；

t——時間；

{u}——結構的位移向量，{u}∈Rn；

{u·}——結構的速度向量，{u·}∈Rn；

{u¨}——結構的加速度向量，{u¨}∈Rn；

v——流體運動速度，m/s；

ρ——流體密度，kg/m3；

τ——剪應力張量。

如果對流體做出如下假設： 流體是無粘性的，可壓縮的，無流動的，流場中整體的平均密度和壓強是均勻的；則上述流體的連續性方程和動量方程就可以簡化為聲波方程：

式中 c——聲波在流體介質中的傳播速度，m/s；

k——流體的體積壓縮模量，N/m2；

P——聲壓，N/m2；

ρ0——流體的平均密度，kg/m3。

根據對流體的簡化，在流體和固體的交界面上，流體法向壓力梯度和固體法向加速度的關系如下：

式中 {n}——耦合面的單位法向量；

{▽P}——壓力梯度差。

如果考慮耦合面的影響，則聲波方程可離散為：

式中 ［CP］——流體阻尼陣；

［KP］——流體剛度陣；［MP］——流體質量陣；

{p}——流體方向矢量；{p·}——流體速度矢量；

{p¨}——流體加速度矢量；ρ0［R］T——耦合質量陣。

3 固定管板換熱器模型與求解

流固耦合分析方法主要有單向流固耦合和雙向流固耦合兩種。 其中，雙向流固耦合是耦合截面上的雙向數據傳輸，固體對流體的影響效果較為明顯，不可忽略；單向流固耦合是指耦合截面上數據的單向傳輸，固體對流體的影響作用相對于流體對固體的影響作用效果甚微，分析過程主要是流場分析和結構場分析，而結構場的分析基于流場分析結果。

在此，筆者采用單向流固耦合方法來對固定管板換熱器進行分析，考慮到固體與流體之間的相互作用力，通過Workbench平臺，先進行Fluent流場分析，再將流場分析的計算結果通過耦合面傳遞給換熱管，從而進行結構應力場分析，分析完后進行模態分析。 計算流程如圖1所示。

圖1 流固耦合分析流程

筆者所用模型為固定管板換熱器 （圖2），筒體尺寸規格為φ219mm×4mm，換熱管尺寸規格為φ50mm×2mm，換熱管長1 500mm，個數為7且排列角為60°，殼程流體流動方式為上進下出，管程流體流動方式為右進左出， 進出口尺寸規格為φ80mm×4mm，殼程流體介質為水。

圖2 固定管板換熱器模型

4 固定管板換熱器流體對管束振動特性的影響

4.1 殼程流體

為了研究殼程流體對管束振動的影響，選取兩種流速下換熱管的固有頻率進行對比，流場分析后，得到等效應力云圖如圖3所示。

圖3 不同殼程流速下的換熱管等效應力云圖

由圖3可知，當流速從0.3m/s上升到0.6m/s時，換熱管的最大等效應力從2.014 3MPa 上升到6.522 1MPa。進行模態分析，得到換熱管前六階固有頻率見表1。 分析表1中數據可知，在同一流速下，換熱管的前六階固有頻率隨著階數的增大而增大；在同一階數下，固有頻率隨著殼程流速的增大而減小，可見固定管板換熱器殼程流速的增大對換熱管固有頻率具有削弱作用。

表1 不同殼程流速下換熱管的前六階固有頻率

4.2 管程流體

設置流場分析的邊界條件為：管程速度入口（Velocity inlet），流速分別設置為0.1、0.3、0.6m/s；其他條件與殼程流場設置一致。 流場分析結果是： 壓力梯度從換熱管入口處往出口處遞減，出口速度低于入口速度，換熱管中心速度最高并向四周遞減。 通過耦合面添加流場分析結果，在靜態應力場中得到等效應力云圖如圖4所示。 由圖4可知，當流速分別為0.1、0.3、0.6m/s時，換熱管的最 大 等 效 應 力 分 別 為65.712、438.860、1 077.300Pa；隨著管程流速的增大，換熱管所受到的等效應力越來越大，且出現位置均在流體入口處。

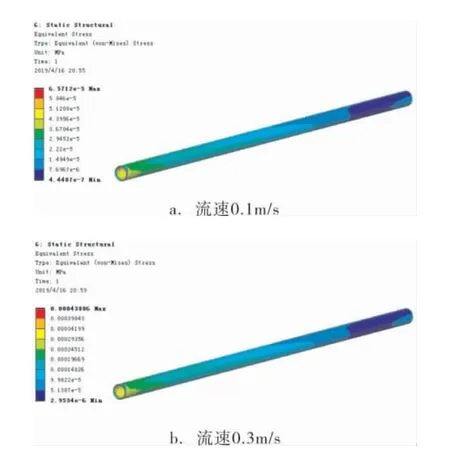
圖4 不同管程流速下的換熱管等效應力云圖

對流固耦合分析后的換熱管進行模態分析，得出不同管程流速下的換熱管固有頻率值 （表2）。 分析表2中的數據可知，在同一流速下，換熱管的前六階固有頻率隨著階數的增大而增大；在同一階數下，固有頻率隨著管程流速的增大而減小，可見固定管板換熱器管程流速的增大對換熱管固有頻率具有削弱作用。

表2 不同管程流速下換熱管的前六階固有頻率

5 結論

5.1 通過對比不同殼程流速下換熱管的固有頻率值，可以發現殼程流速對換熱管固有頻率起著削弱作用，依據GB/T 151—2014《熱交換器》附錄C中換熱管固有頻率的經驗公式可知， 在殼程流體作用下，換熱管單位長度的質量是空管質量加上被換熱管排開的、虛擬的管外流體質量，因此在殼程流體的作用下換熱管的固有頻率會降低，并且隨著殼程流速的增加，固有頻率降低。

5.2 通過對比不同管程流速下換熱管的固有頻率值，可以發現管程流速對換熱管固有頻率起著削弱作用，依據相關標準，在管程流體作用下，換熱管單位長度的質量為空管質量加上管內流體的質量，根據半經驗公式，換熱管單位長度的質量越高，換熱管的固有頻率越低，隨著固定管板換熱器管程流速的增加，固有頻率降低。