復合材料壓力容器的可靠性優化設計

林 峰 馮明揚

（1.楊凌職業技術學院機電工程學院；2.中國電子科技集團公司第三十八研究所）

復合材料由于具有突出的優點，在各領域得到了廣泛應用［1］。但是，由于復合材料組分的復雜性，導致其本構參數、外部載荷等多種參數都具有諸多的不確定性，對于不確定性問題，通常考慮的是隨機性問題［2］。 隨機分析的關鍵在于確定每個隨機參數的概率密度函數，因此需要充足的概率統計信息。 目前，研究學者們對結構隨機可靠性方法進行了諸多研究［3～7］，而對復合材料壓力容器結構可靠性設計的研究卻很少。 為此，筆者對復合材料壓力容器進行可靠性優化設計，為復合材料壓力容器的可靠性預測與設計提供一種簡便可行的方法。

1 壓力容器模型及可靠性分析依據

1.1 壓力容器模型

采用ANSYS 軟件中的SHELL181 單元類型建立壓力容器殼體結構模型，如圖1 所示。 壓力容器結構采用T800 碳纖維，正交鋪設，共8 層，層厚1mm。 球形封頭直徑為350mm，筒體段是外徑為350mm 的圓柱，圓柱段長500mm，設計內壓力載荷為3.2MPa。 由于壓力容器模型是對稱的，為了減少計算時間， 取有限元模型的1/2 進行分析計算，同時對球形封頭頂端施加固定約束。

圖1 復合材料壓力容器殼體結構模型

考慮到后續Monte-Carlo 模擬需要多次迭代，為了提升計算效率，需要合理選擇有限元網格數量。 通過對最大環向應變值的比較，最終選用2 000 個網格對有限元模型進行網格劃分， 此結果比更多數量網格的有限元模型更為保守，且不會造成結構失效。

1.2 可靠性分析依據

如圖2 所示，環向位移主要發生在直徑不變的直筒段和直徑開始變化的球形封頭與直筒段結合部位，最大環向位移發生在曲率半徑變化的部位，所以該部位是最容易發生失效的。分析圖3可知， 應力與應變同圖2b 環向位移的變化趨勢一致，為此可選環向最大總應變（US）作為可靠性分析依據， 只要計算該值小于許用值的概率，就可計算出可靠度。

圖2 形變和位移云圖

圖3 應力與應變云圖

2 基于ANSYS 的壓力容器可靠性分析

Monte-Carlo（MC）方法是一種基于統計學原理來解決隨機問題的數學方法，是用來驗證隨機可靠性分析結果準確性的唯一方法。

在工程實際中，考慮到結構所承受的外載及其自身結構參數、本構特征參數（包括彈性模量Ex、Ey和Ez，剪 切 模 量Gxy、Gxz和Gyz，單 層 纖 維 厚度h，內壓力載荷p 等）的隨機性，設定這些參數均服從正態分布，詳見表1［8］。

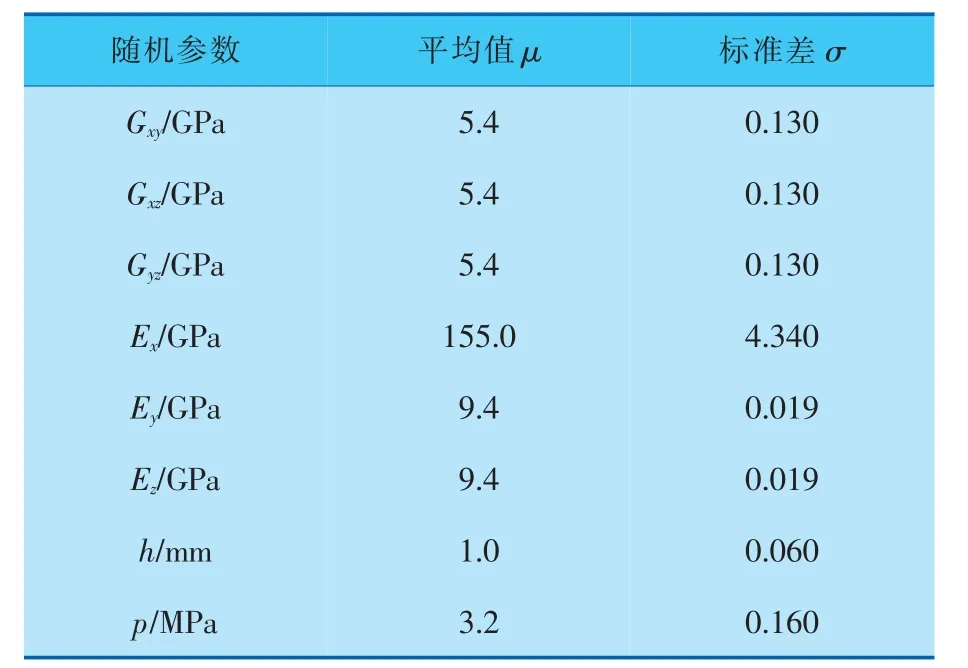
表1 隨機參數的正態分布

極限狀態函數為：

其中，當Z（X）＜0 時為失效狀態，故該結構的可靠度即為Z（X）＞0 的概率；es為復合材料層合板在設計載荷下的許用拉伸應變，其值為0.007 6；emax為環向最大總應變（US）。

以環向最大總應變（圖4）為例，進行5 000次數值模擬計算，藍色曲線表示MC 迭代不同次數計算出的參數均值，上下兩條紅色曲線表示置信度為95%時區間的上下界。 由圖4 可以看出，在迭代次數達到3 750 次之后環向最大總應變均值基本保持不變，說明此時迭代次數已足夠。 因此，為了保證精度、提高計算效率，后續MC 模擬計算采用4 000 次的迭代次數。

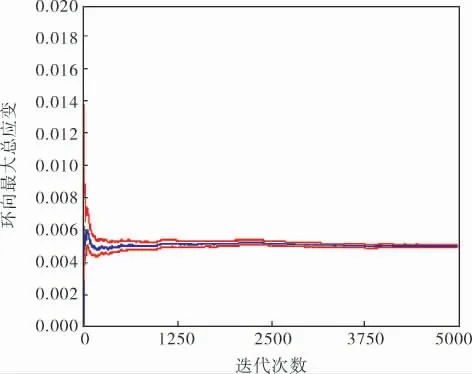
圖4 環向最大總應變隨MC迭代次數的變化曲線

圖5 是環向最大總應變的概率密度分布直方圖，即概率密度函數圖像，對它進行積分即可得到圖6 所示的概率累積分布函數。 由圖6 可以看出，環向最大總應變為0.007 6，對應的概率值是99%，即此時結構的可靠度為99%。

圖5 環向最大總應變的概率密度分布直方圖

圖6 環向最大總應變的可靠度分布

3 基于可靠度的優化設計

優化設計之前有必要先對輸入參數進行靈敏度分析，找出對結果影響大的輸入參數，同時忽略影響較小的參數，從而提高計算效率。 通常，靈敏度大于2.5%的參數為顯著影響因素， 小于2.5%的參數可以忽略。

輸入參數的靈敏度分析如圖7 所示，可以看出， 輸入參數h、p、Ex和Gxy均為顯著影響因素，其中h、Ex和Gxy對結果呈負相關性，p 對結果呈正相關性，而其他參數可以忽略。

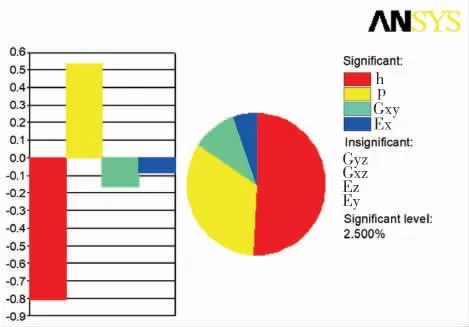
圖7 輸入參數的靈敏度分析

優化設計時， 設Ex和Gxy是設計變量（DV），US 和p 是狀態變量（SV），h 是目標變量（OBJ）。

內壓力載荷p 為3.2MPa，經過10 次迭代，得到優化結果見表2， 將優化結果帶入可靠性模型進行驗證，得到可靠度為99%。 優化結果中h 為0.804 9mm，小于設計初始的1mm 單層厚度，此時材料力學性能得到了充分發揮， 既節省了材料，又滿足了可靠性要求。

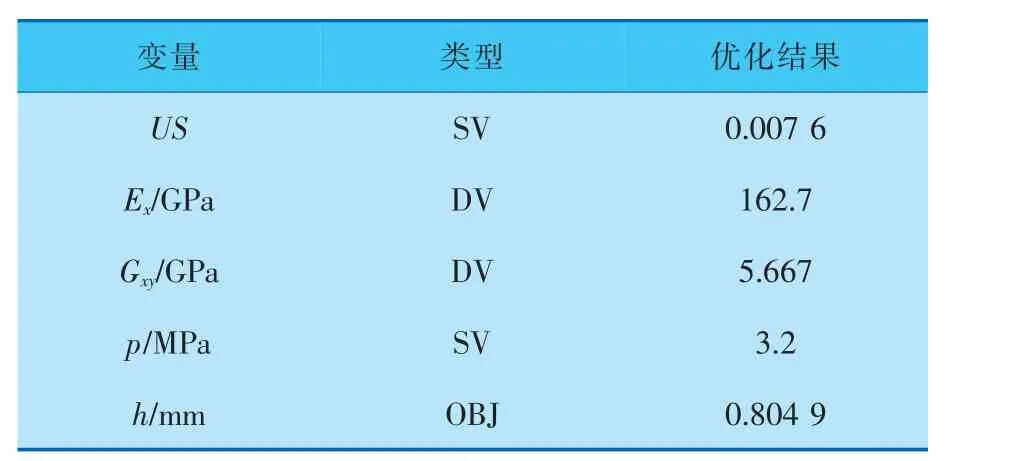
表2 優化結果

4 結束語

筆者針對某航天工程中的復合材料壓力容器進行了結構可靠性優化，建立了復合材料壓力容器的有限元模型， 基于ANSYS 有限元軟件的可靠性分析模塊，計算了結構的可靠度，并基于可靠度對該結構進行了優化設計。 結果表明，采用基于可靠度的優化設計，既能滿足結構安全要求，又能充分節省材料。