問題驅動理性思辨
高燕


摘 要:本文旨在通過對高中數學教學內容進行分析,探討問題教學對高中數學教學的影響,研究問題教學對提升高中生的學科素養有哪些重要意義,以及數學思維在數學教學中的重要性,從而找到更加有效的高中數學教學策略。高中數學的學習不僅是為了讓高中生掌握數學知識,同時也是為了使學生的思維更加活躍、開放,提高高中生的邏輯推理能力和發現、分析、解決問題的能力以及學生的綜合能力。高中數學是非常重要也是非常基礎的一門學科,豐富有趣的數學課堂以及具有創新性的數學教學方法,是提高高中生數學學習興趣的關鍵。高中是培養學生數學思維的關鍵時期,在高中數學教育中注重培養學生的數學思維,會讓學生們更加輕松的學習數學,增加學生對數學的興趣與熱愛,提高學生的綜合能力。
關鍵詞:高中數學,問題教學,數學思維
問題教學是指在課堂前進行有效的預習,帶著自己的問題進行聽課,在課上有針對性的進行學習,提高學習效率。教師可以以例題的形式進行教學,把生澀的知識放在具體的問題中進行講解,更有利于學生的理解。數學思維是一名學生最基本的思維能力,決定著學生以后思考問題的方式,分析問題的角度,解決問題的能力。高中數學的學習主要是為了鍛煉學生的學習能力以及邏輯推理能力。在高中數學教育中,思維教學和創新教學至關重要,不僅可以使學生更高效的掌握數學知識點,靈活應用數學知識,同時也可以培養學生的整體思維能力和理解分析能力。在以往的研究中,很多學者已經對如何豐富高中數學課堂以及如何應用創新教學方法來進行高中數學教學做了大量的研究,我們可以在前人的基礎上,結合自身的實際情況作進一步的分析。
一、正弦定理和余弦定理
正弦定理和余弦定理是在初中已經學過的直角三角形中的邊角關系的基礎上通過對三角形邊角關系的研究,進一步發現并掌握三角形中的邊長與角度之間的數量關系。這部分知識的學習主要是通過了解正弦定理和余弦定理的推導過程,掌握正弦定理和余弦定理的應用;通過用正弦定理和余弦定理理解三角形,判斷三角形的形狀;通過對正弦定理和余弦定理的探究,培養學生發現數學規律的思維與能力,培養學生獨立思考問題,解決問題的能力。正弦定理:在一個三角形中,各邊和它所對角的正弦相等。余弦定理:三角形中任何一邊的平方等于其他兩邊的平方的和減去這兩邊與它們夾角的余弦的兩倍積。
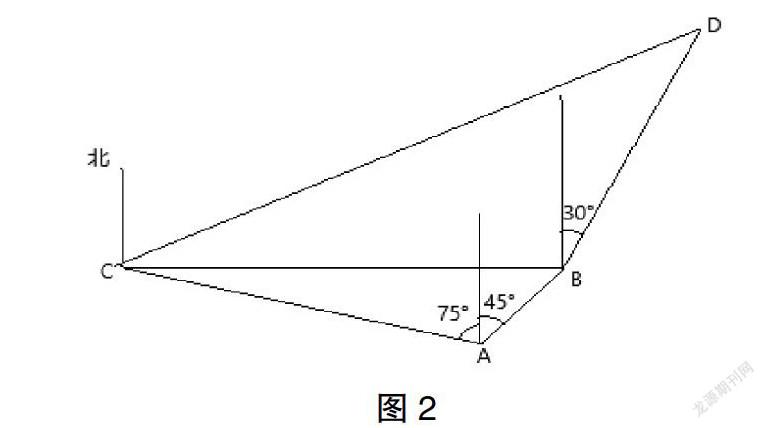
例如,如圖1所示,在海岸A處,發現北偏東45°方向,距A處(√3-1)海里的B處有一艘走私船。在A處北偏西75°方向,距A處2海里的C處的緝私船奉命以10√3海里/h的速度追截走私船。此時走私船正以10海里/h的速度從B處向北偏東30°方向逃竄,則緝私船沿什么方向行駛才能最快截獲走私船?并求出所需要的時間?
分析:本題屬于一個追及問題,在以前學習的直線運動中,一般是先求出BC的長,再利用在相同的時間內,一個走CB+BD這段的長,另一個走BD的長,在D處相遇列方程求解,而在本題中這個時間并不是最短的,緝私船可以由C直接到D,這時CD<CB+BD,可求出最短的時間及∠BCD,此外需要注意的是,緝私船所走的距離并不等于相同時間內走私船的距離加上BC。
注意,在做這類題時,要先畫出圖形,將方向角準確的轉化成三角形的內角,然后把正弦定理和余弦定理相結合起來,解決問題。數學學習主要是培養學生靈活的思維能力,以及條理清晰的數學邏輯思維,學生應該輕松地把書本知識應用到生活中,應用知識把生活變得更加簡單、方便。
二、圓的方程
圓的定義和性質的學習是高中幾何數學學習的基礎,也是進一步研究空間問題的前提,圓的方程屬于解析幾何中的基礎,是以二次曲線為著手點,為后續圓與直線的關系、圓與圓的位置關系等的學習打下基礎。所以,掌握圓的標準方程的形式,會求圓的標準方程,會判斷二元二次方程表示圓的條件及用一般式求圓的方程,了解二元二次方程,圓的標準式方程,圓的一般式方程三者之間的關系在高中幾何數學學習中至關重要。在圓的標準方程中,平面直角坐標系中的點(a,b)都可以作為圓的圓心,任何大于0的實數r都可以作為圓的半徑長。滿足方程的點(x,y)都在圓上,圓上的每一點的坐標都滿足方程。以C(a,b)為圓心,r為半徑長的圓的標準方程式為:(x-a)2+(y-b)2=r2。r是圓的半徑長,所以方程的右端的r肯定大于0。
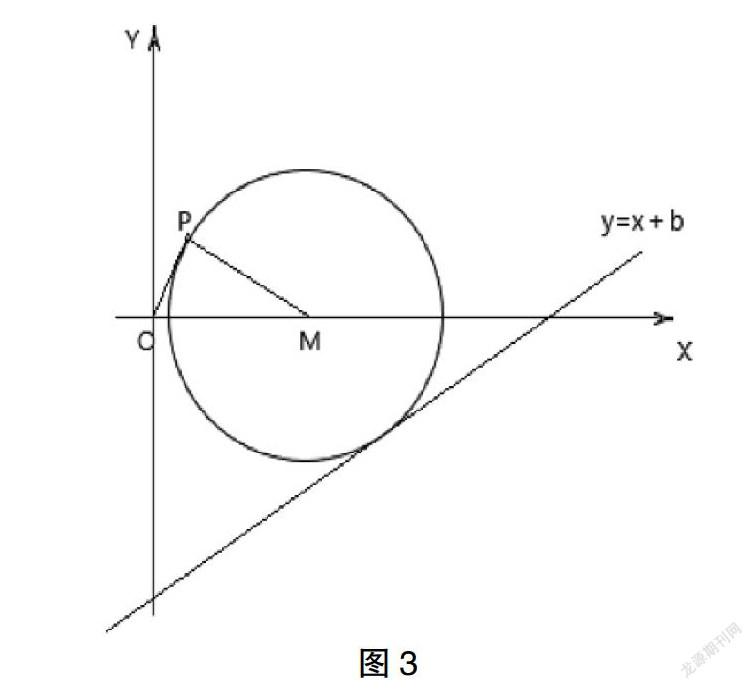
例如,已知實數x、y滿足方程x2+y2-4x+1=0;
求:(1)y/x的最大值;(2)y-x的最小值?
分析:將實數x、y看作P點的橫、縱坐標,滿足x2+y2-4x+1=0的P(x,y)的軌跡是以點M(2,0)為圓心,為半徑的圓,如下圖3所示。利用數形結合解決最值問題時,先從代數演算入手,將代數表達式賦予幾何意義,看成某幾何量,把問題轉化為求此幾何量的最值問題;再從幾何圖形出發,根據圖形的幾何性質觀察出最值出現的時機和位置,從而解決求代數表達式的最值問題。
注意,求圓的方程時,首先應依題意恰當地選擇所求圓的方程的形式,然后充分利用幾何性質解題。注意,在做幾何題時,可以更多的使用畫圖法,把文字描述轉化成圖的形式,以更加直觀的形式呈現已知條件。在求圓的標準方程式時,最常見的呈現方式就是與直線相結合,所以要很好的掌握一元一次方程和二元一次方程的求解方法,為幾何計算打好基礎。圓的方程一般不會單獨出現,多結合直線和坐標系進行考核,這就培養了學生善于思考、善于發現的能力,使學生具備敏銳的洞察力,很容易發現事物之間最緊密地聯系。
數學思維是一名學生最基本的思維能力,決定著學生以后思考問題的方式,分析問題的角度,解決問題的能力。問題教學,是把生澀難懂的知識放在具體的例子中,使得知識點更加清晰易懂,另外,例題教學可以使很多知識綜合在一起,使得學生學會分析知識之間的聯系。所以,高中數學主要應該以例題教學為主,培養學生的數學思維和數學能力。
參考文獻
[1]梁旦.基于邏輯思維視野下高中數學教學策略探究[J].科學咨詢(教育科研),2020(09):252.
[2]邱春亮.基于探究能力培養的高中數學教學[J].數理化解題研究,2020(24):9-10.
[3]李玉卓.核心素養背景下高中數學教學策略探析[J].讀寫算,2020(22):98-99.

