淺談借助分支圖解決數學問題

鮑妙森

摘要：在小學數學中，解決問題的重要性不言而喻，本文結合具體問題，借助分支圖對問題進行清晰合理的分析，闡述解決問題中通過審題并列出式子的過程，歸納出基于核心素養的審題列式策略，以提高學生的解題能力，培養應用意識和創新意識。

關鍵詞：小學數學;解決問題;列式

“解決問題”考察了學生的各項綜合能力，是小學數學非常關鍵的內容，呈現形式往往是情境豐富，背景鮮活，文字冗長，類型多變，對于正處于由形象思維向抽象思維過渡的小學生來說，理解起來困難較大。如果不掌握一種直觀而又科學的分析方法，不斷開拓解題思路，提高解題能力，長此以往將極大地挫傷學生學習的積極性。

問題 ：用濃度45%和5%的糖水配制成濃度為30%的糖水400克，則需要這兩種糖水各多少克？

這個問題有一定的難度，其中的內涵需要借助分支圖加以深刻的理解，從而歸納出解決問題中審題并列出式子的通用方法，擺脫“教師難教，學生難學”的現象。

一、明確各個量，構建數量關系

解決問題所需要的信息要從問題入手尋找，在明確問題的基礎上收集信息，引導學生整理問題中的各個量，立足于解決問題的本質。仔細審題是正確解題的前提，需要對問題進行審讀，分析題目中的相關對象，把題目中的各個量提取出來，分析量與量之間的關系，即構建數量關系。

1.明確對象，梳理數量

學生在解決問題時，必須先要把題中的數量關系理清楚。數量關系是解決問題的靈魂，任何問題都是通過數量關系來體現的。在解決問題時只要理清數量關系，問題也就迎刃而解了。

這是糖水配比問題，題目中的對象：

（1）濃度45%的糖水;

（2）濃度為5%的糖水;

（3）“混合”之后30%的糖水，

為了方便起見，我們記作高糖水，低糖水，混合糖水，類似的，如其中的含糖量分別記為高糖，低糖，混合糖。

題目中的量相對清晰，就是糖的質量，水的質量，糖水的質量，糖水的溶度。

2.合理分類，搭建關系

一般解決問題題型都是由已知條件和問題兩部分組成，對已知信息進行合理分類，分析數量之間的關系是審題的核心環節。由于小學生閱讀理解的能力有限，錯誤判斷題意，因此要引導學生關注關鍵詞，以及重要句中所涉及的數量關系。

3.正確選擇，建立聯系

引導學生從題目中提煉出有用的數學信息，根據題意進行合適的選擇，忽略與本題無關的數量關系，推敲題目中的字詞，發掘出隱含條件，排除一些冗余條件。較為復雜的問題還需要構建不同數量關系之間的內在聯系，從而為后續解題奠定必要的基礎。

梳理出解決問題相關的數量關系，這個問題有關的數量關系是：

② 糖水的質量×糖水的濃度=糖的質量;

③ 高糖+低糖=混合糖;

⑤ 高糖水+低糖水=混合糖水，

這個時候我們需要思考這三個數量關系之間存在著必然的聯系，并搭建它們之間的聯系，依托“②糖水的質量×糖水的濃度=糖的質量”，可以把“③高糖+低糖=混合糖”和“⑤高糖水+低糖水=混合糖水”這兩個貌似相差甚遠的兩個數量關系有效的連接起來。

學生思得如何，需要教師引導學生有條理、有邏輯地思考問題，使學生能夠全面分析解題的思路，促進學生邏輯思維能力的發展，提高學生運用數學知識、解決實際問題的能力教師不但要留給學生充分思考的余地，使學生主動而積極地產生遐想，引發思維的火花，剛要關注每一個學生的思維活動，為學生提供獨立思考的機會，力求“實現不同的人在數學上都得到不同的發展”。

二、表示各個量，形成分析策略

1.搭建主框架

主框架的搭建其實是建立在數量關系以及彼此關系的基礎上，用分支圖可以更加清晰展現各種量之間的聯系。

2.表示各個量

任何問題在題目中都存在已知量和未知量，有些量是比較明顯的，可以直接列舉出來;但是有些量不太明顯，則可以借助完整數量關系逆向導出缺失量。利用分支圖分析問題時，學生可以通過讀題來明確問題，尋求條件，從而將已知量和未知量表示在分支圖中，有助于實現學生的思維由外化至內化的轉化過程。例如本題有關的關系：② 糖水的質量×糖水的濃度=糖的質量;

③ 高糖+低糖=混合糖;

⑤ 高糖水+低糖水=混合糖水，

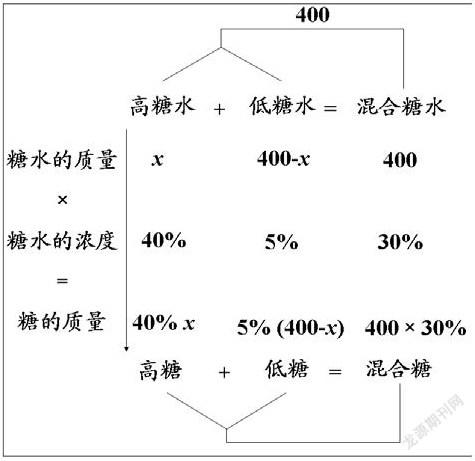
根據缺失量可以有計劃的設未知數，利用數量關系表示各個量，有的時候需要把數量關系進行變形來表示不同的量，這個要根據設立的未知數，結合題意進行合理分析。本題我們可以設高糖水為x克，因為混合糖水為400克，所以低糖水可以表示為（400-x）克，糖水的濃度都是知道的，可以順次填入，通過糖水的質量×糖水的濃度=糖的質量，表示出糖的質量，由此分支圖中的所有空缺處都填入了表示各個量有關的數或含字母的式子。

3.列出關系式

有些問題往往并不是直接地出現解答的思路，而是需要學生對問題的數量關系等進行分析才能正確地解答。分析和抽象對于正確地列出式子，解決實際問題是至關重要的。

根據高糖+低糖=混合糖，從分支圖中，可以很容易的列出式子。解決問題需要相應的策略來支撐對問題的分析、思考，讓學生了解和形成解決問題的一些基本策略。建構主義認為，學生的建構不是教師傳授的結果，而是通過親歷、通過與學習環境的交互作用來實現的。從學習角度看，學習既是一個內化的過程，同時也是一個外化的過程。

借助分支圖法解決問題，可以把思維過程具體清晰地呈現出來，讓蘊含在題目背后各個量之間的關系躍然紙上。學生可以透過豐富的背景提煉出解決問題的脈絡，通過形象直觀的學習來積累活動經驗，感受分析問題的殊途同歸，這樣即能培養學生問題解決的能力，還能提高他們的數學素養。

參考文獻：

[1] 周彬.《課堂密碼》[M].上海：華東師范大學出版社，2009.

[2] 中華人民共和國教育部.《義務教育數學課程標準（2011年版）》[M].北京，北京師范大學出版社，2012.

浙江省永嘉縣沙頭鎮花坦小學 浙江 永嘉 325109