參數優化VMD對變壓器聲音信號的故障診斷

魏才懿，楊 軍，馬建橋

(1. 蘭州交通大學 自動化與電氣工程學院，蘭州 730070；2. 蘭州交通大學 測繪與地理信息學院，蘭州 730070)

變壓器的可靠性在電網的高效穩定運行中具有至關重要的作用，及時診斷出變壓器的局部放電能有效預防其發生故障[1].目前，變壓器內部局放故障的常用診斷方法主要有脈沖電流法[2]、超聲法[3]和油色譜分析法[4]等，這些方法易造成變壓器的二次損壞，而變壓器聲音信號蘊含了故障狀態的重要信息，在一定程度上反映了變壓器內局放故障情況，長期一線工作的檢修員通過耳朵可以對變壓器運行狀況進行大致判斷，但無法對其內部故障定性判斷，這種普遍使用的診斷方法在很大程度上依賴于技術人員的主觀判斷和個人經驗，具有很大的不確定性.但這一現象證明了利用可聽聲信號診斷變壓器故障的可行性，借助于聲音傳感器和現代數字信號處理技術，可實現比人工更客觀、更可靠的在線監測和故障診斷[5-6].由于變壓器內部局放聲音信號受傳播介質影響，呈現出短時隨機脈沖的特點，導致提取的故障特征不能充分表征故障樣本，進而影響到故障類型識別的準確率.研究者一般采用小波包變換[7]、頻率響應分析[8]等方法對故障信號進行處理.但這些方法都依靠人的經驗來設置參數進行分解，對于復雜的局放聲信號，可能會造成故障特征信息的丟失或冗余，使故障診斷的性能受到嚴重影響.故從聲音信號中提取高質量的故障特征信息是整個故障診斷的關鍵.

變壓器聲音信號會伴隨其內部絕緣故障放電時產生非線性非平穩性信號.為得到能夠表征不同類型放電的有效特征信息，目前常用的放電特征提取方法有小波特征法[9-10]、經驗模態分解(empirical mode decomposition,EMD)[11-12].小波特征法是基于小波分解的特征提取方法，實質上是一種傅里葉變換，需要選擇適合的小波基和分解層數，并且不具備自適應性.EMD相對小波分解，不需要做預先分析與研究，自動按照一定固有模式按層次分好，雖然減少了人為干預和設置分解層數，但在分解過程中存在端點效應和模態混疊(一個單獨的本征模態分量(intrinsic mode function,IMF)信號中含有不同的時間尺度)等問題.此外，Smith[13]提出局部均值分解(local mean decomposition,LMD)方法來改善EMD的缺陷，但該方法抗干擾能力差，受分解層數的影響容易出現不收斂等問題，和EMD一樣LMD也受限于遞歸模式分解框架中.Dragomiretskiy等[14]于2014年提出變分模態分解方法，其利用非遞歸的技術對信號分解，通過引入變分模型，將信號分解問題轉化為約束模型的尋優問題，可以實現各信號分量頻率的分離，避免LMD及EMD存在的模態混疊等問題.

針對變壓器故障聲信號特征提取不佳而導致診斷識別率低的問題，提出模擬退火優化變分模態分解—樣本熵(simulated annealing variational mode decomposition sample entropy,SA-VMD-SE) 的特征提取方法.VMD中分解層數K和懲罰因子α的選擇沒有規律，通常按研究者的經驗選取，本文首先將模擬退火算法(simulated annealing,SA)[15]應用于兩參數全局尋優，利用最優參數設置VMD分解故障聲信號，得到反映不同頻帶特征的本征模態函數；其次求取衡量各分量復雜程度的樣本熵作為表征故障樣本的特征；最后將求得的樣本熵作為SVM分類器的輸入特征向量進行故障識別與診斷.

1 變分模態分解

變分模態分解[14]將一個原始信號f分解為K個IMF，第k個IMF分量的表達式為

uk(t)=Ak(t)cos(φk(t)),

(1)

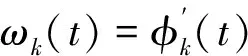
通過如下步驟計算每個IMF分量的帶寬：

首先，對每個本征模態函數uk(t)進行Hilbert變換，計算模態函數的解析信號，即

(2)

其次，通過混合模態解析信號與預測信號中心頻率e-jωkt，將每個模態的頻譜調制到對應的基頻帶，如下所示：

(3)

最后，計算解調信號梯度的L2范數，估計各IMF分量的帶寬后，為使得各分量的估計帶寬之和最小，構造約束變分模型為:

(4)

VMD方法就是通過求解上述約束變分模型的最優解進而自適應地分解信號.通過引入二次懲罰因子α和Lagrange算子λ(t)(其中:α可以保證噪聲條件下信號的重構精度;λ(t)確保約束條件保持嚴格性)，將該模型的約束變分問題轉化為非約束變分問題求解，如下所示：

(5)

利用交替乘子法(alternating direction method of multipliers,ADMM)不斷更新各本征模態分量及其中心頻率，最后所求上式的凸優化問題即為原問題的最優解.因此，可由式(6)得到所有本征模態分量.

(6)

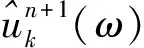
算法中各本征模態分量的中心頻率更新公式如下：

(7)

以上即為變分模態分解全過程，從分解原理來看，VMD雖然規避了EMD的模態混疊問題，但其分解精度受分解層數k以及懲罰參數α的影響.現有對參數的取值往往根據先驗知識，難以保證信號的最優分解，如文獻[16]利用EMD分解后的分量頻率來估計k值的選取，但由于EMD本身模態混疊和端點效應的缺陷，不可避免地會影響k值的結果.因此，尋找合適的參數值是保證變分模態分解的關鍵.

2 基于模擬退火算法的參數優化

上節分析了VMD算法過程中參數α和k對分解的影響，根據經驗定參的設置方法得不到最優的分解效果，而模擬退火算法是Metropolis等[15]基于Monte-Carlo迭代策略提出的求解復雜組合優化問題的一種有效方法，其思想是基于晶體冷卻過程與組合優化問題之間的相似性，通過接受賦予新狀態的過程(一種時變且最終趨于零的概率突跳性)，可有效規避陷入局部最優并最終趨于全局最優解，故本節采用模擬退火算法進行參數優化來得到最優參數組合.其主要步驟為：

Step1設定退火起始溫度T0，冷卻系數q，終止溫度Tend和每個溫度層T下的迭代次數L；

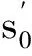
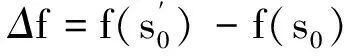
Step4在當前溫度T下對Step2～Step3進行L次迭代循環；

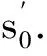
利用模擬退火算法確定VMD的參數時，Step2中需要一個目標函數f(s0)，通過對比目標函數值的大小進行狀態的更新.變壓器局放故障聲信號經過VMD后，若IMF分量中包含噪聲較多，放電時的放電特征則會被掩蓋，此時分量信號的稀疏性弱，包絡熵較大；反之，若IMF分量中包含噪聲較少，則會出現可能的放電沖擊特征，此時分量信號的稀疏性強，包絡熵較小，包絡熵越小說明分量蘊含故障信息越豐富，也說明信號分解得越好.所以用分量包絡熵作為參數尋優的目標函數，時間序列x(j)(j=1,2,…,N)的包絡熵Ep定義為：

(8)

式中：pj是a(j)的概率分布序列；a(j)是序列x(j)經過Hilbert變換后得到的包絡信號.

3 樣本熵

熵為衡量時間序列復雜性的參量.樣本熵(sample entropy,SampEn)是Richman等[17]提出的一種度量時間序列復雜性和統計量化的方法，其物理意義和近似熵類似，都是通過衡量序列嵌入維數變化前后時間序列產生新模式概率的大小說明信號的復雜度.評判原則為：不同維數下與相似容限度差別越大，產生新模式的幾率越大，即熵值越大對應時間序列越無序；相反，若樣本熵值越小，說明自我相似性越高，對應時間序列越規律.由于變壓器局部放電發生時其狀態會發生改變，即會產生不同的聲音，故可以借助樣本熵來計算不同局放故障時的信號復雜度.其計算過程如下：

設長度為N的一維時間序列{x(n)}=x(1),x(2),…,x(N)，按序號組成一組維數為m的向量序列

Xm(1),Xm(2),…,Xm(i),…,Xm(N-m+1),

其中，Xm(i)={x(i),x(i+1),…,x(i+m+1)},1≤i≤N-m+1.這些向量表示第i點開始的m個x的值.

定義向量Xm(i)與Xm(j)之間的距離d[Xm(i),

Xm(j)]為兩者對應元素中最大差值的絕對值，即

(9)

對于給定的Xm(i)，統計Xm(i)與Xm(j)之間距離不大于參數r的數目j(1≤j≤N-m,j≠i)，并記為Bi，則當1≤i≤N-m時，定義

(10)

定義Bm(r)為

(11)

將維數增加到m+1，按照上述公式計算Bm+1(r)，這樣得到的Bm(r)和Bm+1(r)是在相似容限r下分別匹配m和m+1個點的概率.此時該序列樣本熵定義為

(12)

實際樣本序列中N為確定值，樣本熵定義為

(13)

4 基于SVM的變壓器局放故障分類

在得到表征故障的有效特征樣本熵后，需要一個準確的分類器對這些特征進行分類識別.支持向量機(support vector machine,SVM)是Vapnik等在統計學理論基礎上提出的一種有監督學習方法[18]，作為經典的決策算法，SVM在解決小樣本和高維非線性分類問題中具有獨特的優勢和普適性，已經廣泛應用到模式識別和故障預測等諸多領域[19-21].在非線性問題方面，SVM通過引入懲罰系數與核參數將其轉化至高維空間的線性問題，從而實現準確分類，但參數的選擇不同對SVM的分類效果也相差較大，目前許多學者采用智能優化算法進行SVM優化研究[16,22].綜合考慮實驗條件下樣本少及SVM能解決高維非線性小樣本等優點，本文選擇經典的SVM作為變壓器局放故障診斷方法.其原理如下：

假設訓練集為{(xi,yi)},i=1,2,…,M,x∈Rn,yi={-1,1},其中：M為樣本數；x∈Rn為輸入的n維特征空間；yi表示輸出的分類標簽.假定類別是線性可分時，存在如下表達式：

yi(ω·xi+b)-1≥0.

(14)

則超平面表示為

fω,b=sign(ω·x+b).

(15)

因此，SVM模型的求解最大分割超平面問題又可以表示為以下約束最優化問題：

(16)

若線性不可分時，引入松弛因子ξi，則

(17)

對于非線性條件下的分類問題，通過核函數將特征向量x∈Rn映射到高維空間，轉化為線性分類問題，其表達式如下：

K(xi,xj)=Φ(xi)·Φ(xj),

(18)

則式(15)可寫成

(19)

式中，λi為拉格朗日乘子.

綜上所述，本文通過模擬退火算法對VMD進行參數尋優，采用最優參數設定VMD對故障聲音信號進行分解，求取分解后各分量的樣本熵作為故障特征，將這些故障特征分為兩部分，一部分作為訓練數據訓練SVM，另一部分作為測試數據驗證SVM的識別分類結果，最終實現對故障類型的診斷.具體診斷流程如圖1所示.

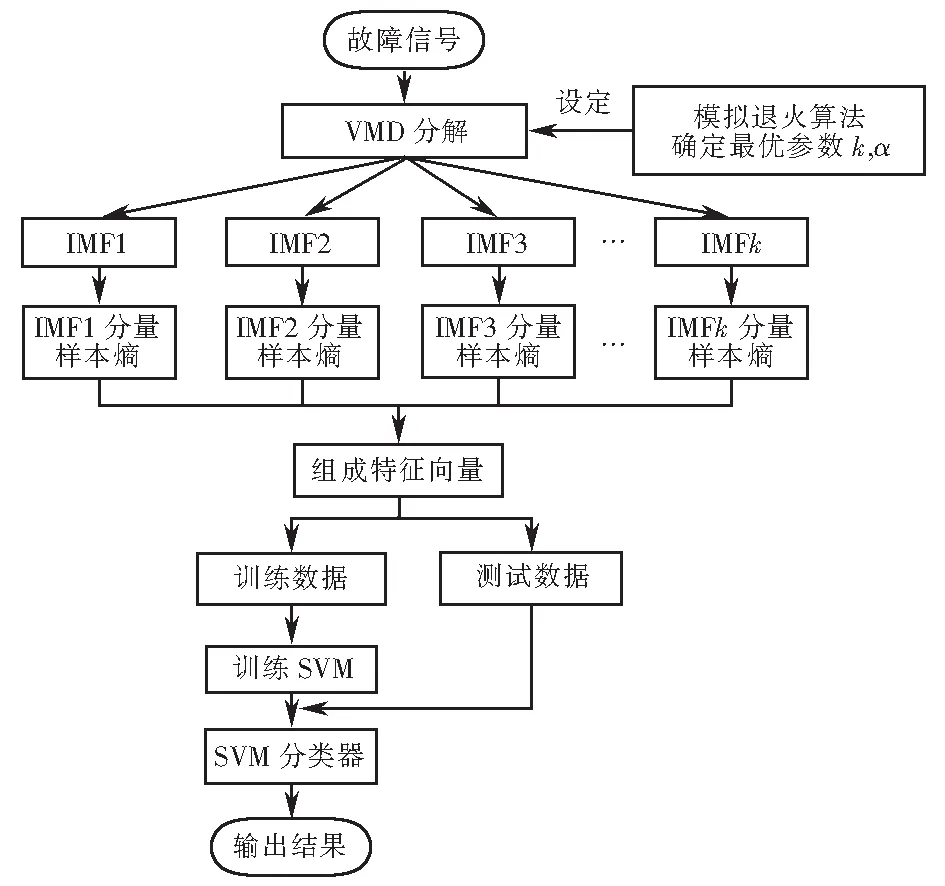
圖1 變壓器故障診斷流程Fig.1 Process of transformer fault diagnosis

5 試驗分析

5.1 模擬信號分析

利用仿真信號來驗證本文所提方法的有效性，設置采樣頻率為5 kHz，模擬變壓器內部局放聲音信號x(t)，主要由50 Hz變壓器基頻信號x1(t)=cos(2π×50t)，偶次諧波信號x2(t)=0.07cos(2π×100t)-0.05cos(2π×200t)+0.02cos(2π×300t)，隨機正弦脈沖信號x3(t)和一組信噪比為5 dB的高斯白噪聲信號x4(t)疊加組成，模擬局放信號如圖2所示.

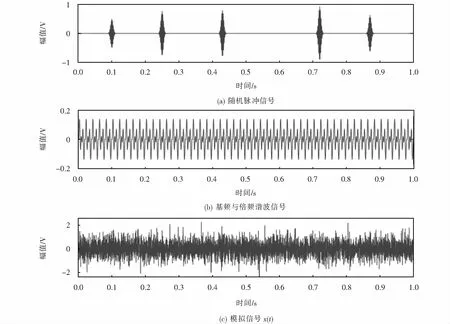
圖2 模擬信號時域波形圖Fig.2 Time domain waveform of simulated signal

設置尋優VMD參數范圍k∈[5,15]，α∈[100,3 000]，模擬退火起始溫度應選的足夠高，使所有轉移狀態都被接受，因此起始溫度與終止溫度值分別設定為10 000 ℃和20 ℃，冷卻系數q=0.95，通過多次迭代來找到對應溫度下最好的解.最終得到最優參數k=5，α=1 800.圖3為退火算法對VMD參數尋優結果圖.

為驗證分解效果，對模擬信號進行EMD分解得到各模態分量時頻圖，對比圖4與圖5可知，EMD分解后IMF7～IMF12與原始信號相關度不大，IMF1～IMF4信號模態混疊現象嚴重，存在虛假分量，對模擬脈沖信號的特征體現不夠充分，而VMD在模擬退火參數尋優后，IMF2與模擬脈沖信號有較高相似度，充分體現了“故障”分量.

5.2 試驗系統平臺搭建

由于變壓器運行中有很多干擾，為獲取聲信號而使用運行的變壓器進行重復局部放電試驗也不合理，因此，為驗證本文方法的有效性，在油中局部放電平臺上進行針板放電、沿面放電和氣隙放電，模擬的3種變壓器內部局放故障模型如圖6所示，三種典型放電試驗對應變壓器內部實際放電故障如表1所列.

模擬局放試驗系統由工頻加壓系統、變壓器局放油箱模型和聲音采集系統組成.局放試驗采用IEC60270:200標準，聲音信號經愛華傳感器AWA14423采集，由于故障可聽聲頻率在2 000 Hz以內[23]，為保證采集到信號質量高保真，按照奈奎斯特采樣定理，設置試驗采樣頻率為5 000 Hz，然后通過前置放大器AWA14604以2 s為樣本時長記錄樣本數據.試驗中為減少水分對油紙模型絕緣介質的影響，事先使用烘干機對絕緣紙板充分烘干去除水分，然后浸泡48 h以備用[24].傳感器安裝在靠近油箱壁中心10 cm處.每種局放模型采集90組數據，在背景噪聲極低的實驗室環境下進行.實驗電路原理如圖7所示.

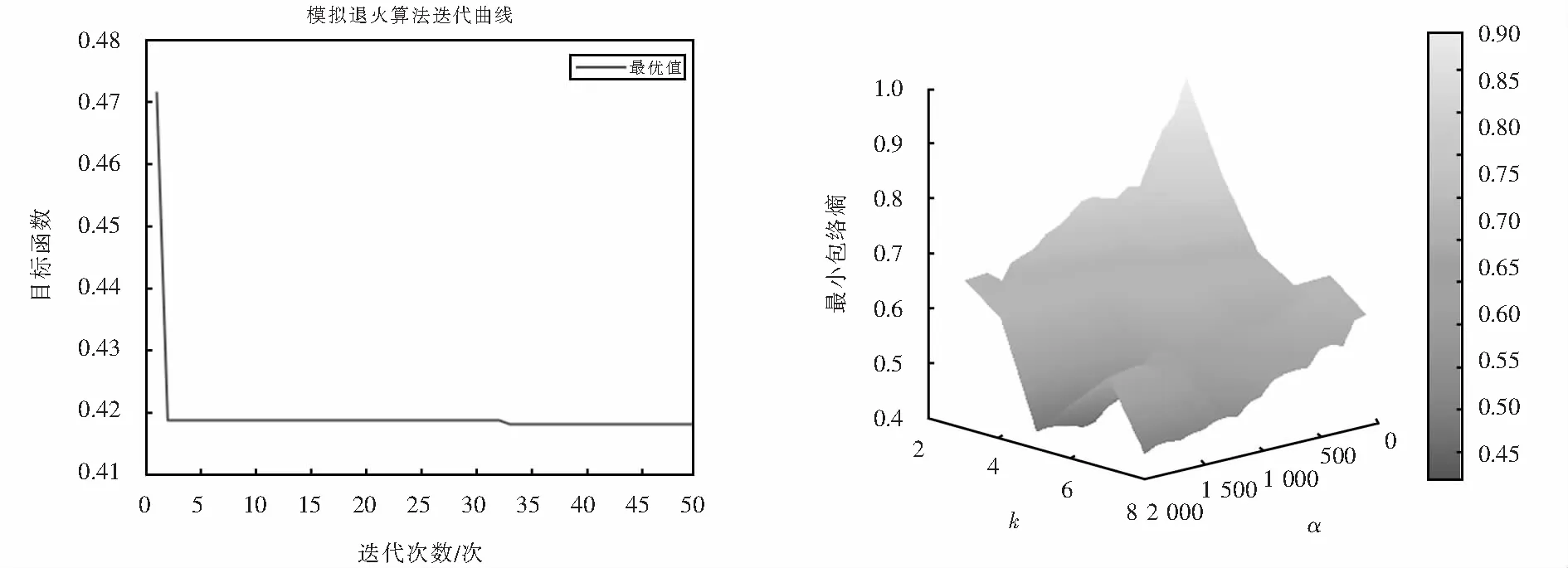
圖3 模擬退火算法尋優結果圖Fig.3 Optimization results of simulated annealing algorithm

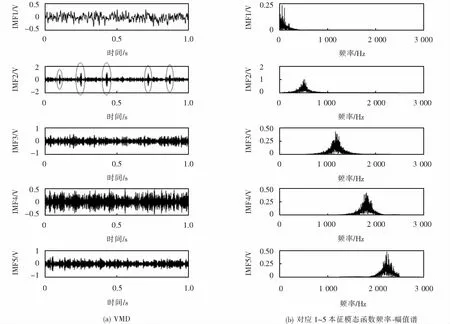
圖4 模擬信號VMD分解時頻圖Fig.4 Analog signal VMD decomposition time-frequency diagram

5.3 仿真試驗數據分析

針對以上試驗系統采集到的3種局放信號，采用模擬退火算法尋優得到3種放電模型尋優迭代曲線與最優參數組合結果如圖8所示.按優化結果最終設置變分模態方法的參數k=7，α=2 800,并分解所有信號；分解后計算樣本熵作為特征量，設定其參數m=2，r為樣本信號標準差的0.1倍，表2為3種放電信號分解后各樣本熵的平均值，將表2繪制成折線圖，如圖9所示.

通過對表2和圖9縱向比較可以看出，3種局放聲音信號分解后的各IMF樣本熵具有較為明顯的差別，表示各模態分量在時間序列上的復雜度不同，較好地反映出了不同放電狀態間的變化和差異，說明所提出的模擬退火優化變分模態分解—樣本熵特征提取方法對局放故障聲音信號特征具有可分性.

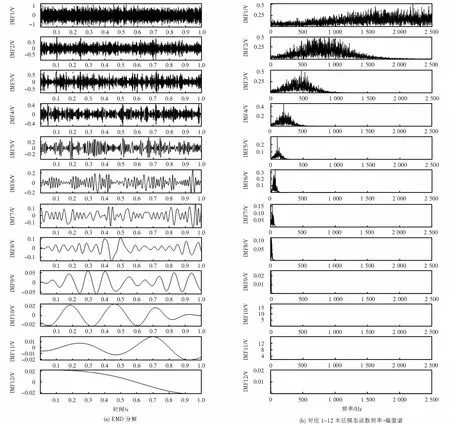
圖5 模擬信號EMD分解時頻圖Fig.5 Analog signal EMD decomposition time-frequency diagram

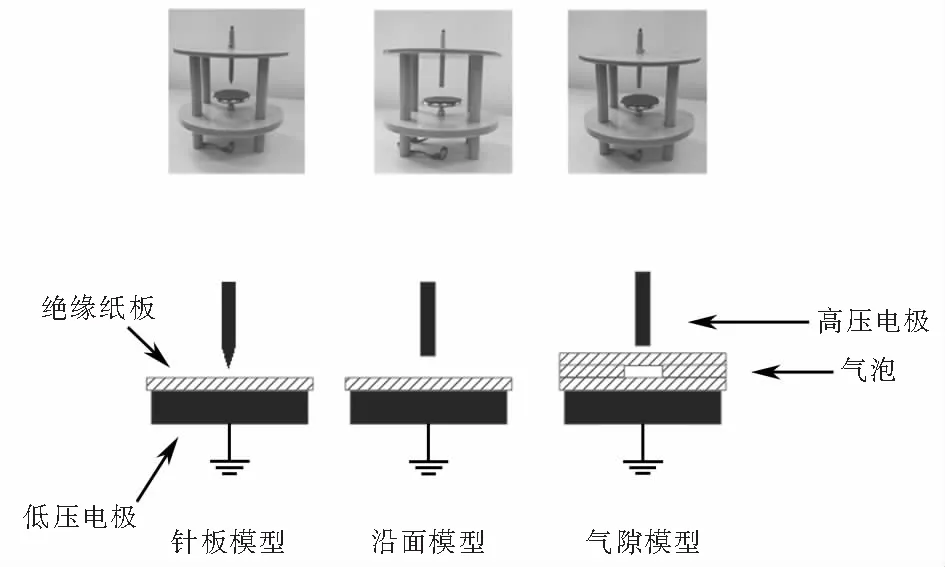
圖6 3種變壓器內部局放故障模型Fig.6 Three kinds of transformer internal local discharge fault models

為驗證本論文方法的有效性及準確性，采用SVM識別不同放電聲音信號，選取3種放電聲音信號共270個樣本(每種類型各90個樣本)，訓練樣本與測試樣本按2∶1設定，故障對應類別標簽為：針板—類別1、氣隙—類別2、沿面—類別3，對SVM訓練后測試樣本識別結果如圖10所示.從圖10可以看出，90個測試樣本中有7個樣本沒有準確分類，測試樣本平均準確率為92.22%.

表1 三種典型局放故障模型對應變壓器內部實際放電故障

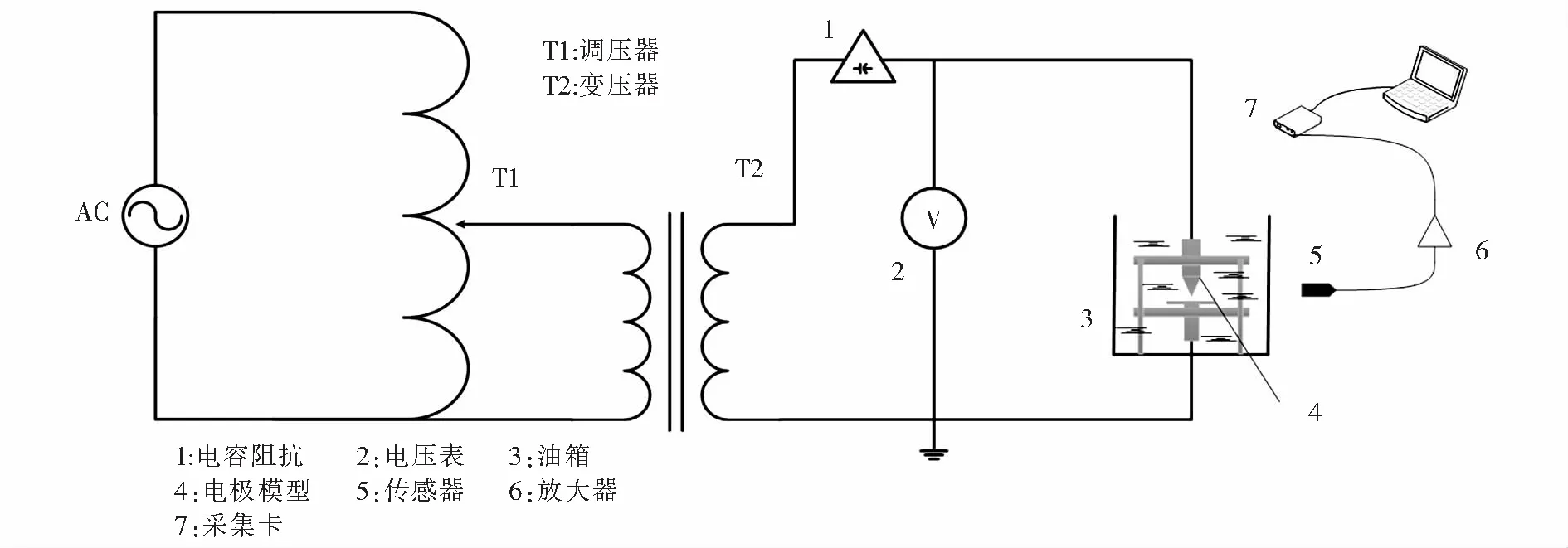
圖7 實驗電路原理圖Fig.7 Schematic diagram of test circuit

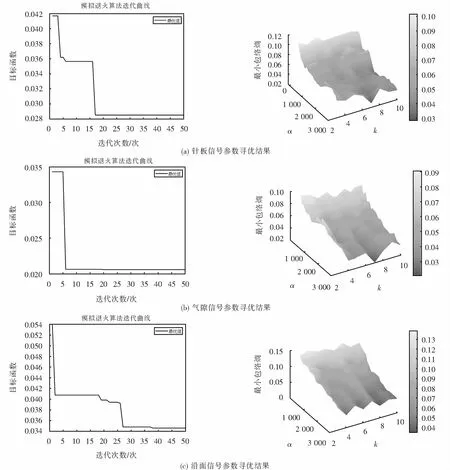
圖8 3種模擬信號最優參數組合結果Fig.8 Results of optimal parameter combination of three analog signals

表2 3種放電信號分解樣本熵平均值

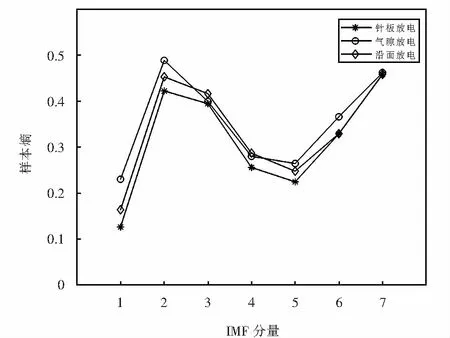
圖9 3種放電信號分解樣本熵平均值Fig.9 Average value of the three kinds of discharge signal decomposition sample entropy

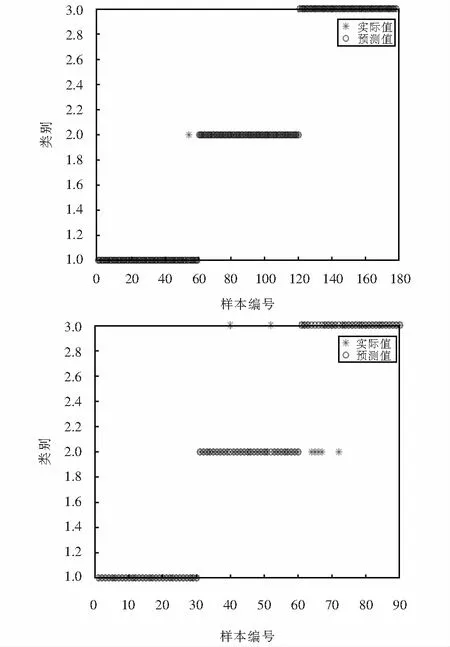
圖10 識別結果圖Fig.10 Recognition result graph

為進一步驗證SA-VMD參數優化對故障模型聲音信號分解的影響，將樣本信號分別按EMD估計與中心頻率估計后的k=6、9，α=2 000設置VMD處理信號，計算樣本熵并識別，測試樣本識別結果如表3所列.可以看出，SA-VMD分解后特征量的識別率達到92.22%，平均識別精度高于其他方法參數設定下的結果，說明模擬退火尋優后的VMD可以更好地分解并得到故障特征，而EMD估計法與中心頻率估計法所得參數未能使VMD準確地分解信號，從而使不同類型故障特征量樣本熵識別率不高.

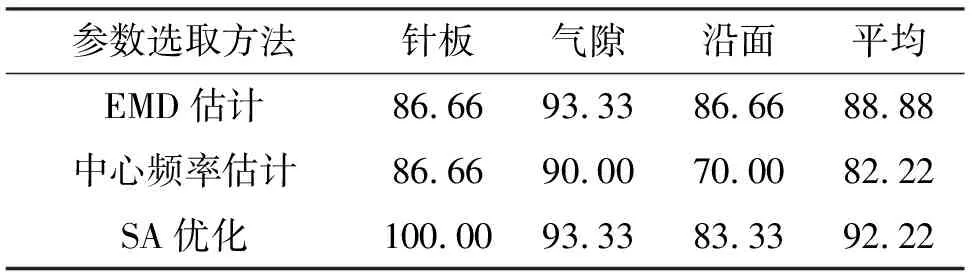
表3 不同參數選取方法下測試樣本識別結果

6 結論

針對估計或給定參數的VMD對變壓器放電故障聲音信號分解不準確從而導致識別精度不高的問題，提出模擬退火優化變分模態分解—樣本熵特征提取的診斷方法，得到以下結論：

1) VMD分解后各模態分量沒有出現模態混疊等現象，對變壓器放電故障模型信號分解較為清晰，可實現對3種放電模型聲音信號的識別與分類.

2) 相比于EMD估計或給定參數的VMD，本文采用模擬退火算法對VMD參數尋優后，各本征模態分量的樣本熵可以更準確地反映故障的狀態變化，從而得到更好的診斷效果.