核心素養視角下學生數學概括能力的引導與培養策略

高紅運

摘 要：概括是思維能力的根本，是引領學生自主歸納和實現知識正向遷移的基礎。結合教學實踐探討核心素養視角下學生數學概括能力的引導與培養策略。

關鍵詞：核心素養;概括能力;引導;培養

作為數學核心素養不可或缺的重要構成，其數學概括能力就是從具有相同特征的事物中找到共同點，并通過抽象歸納總結出這些事物最為本質的屬性。初中數學主要以數學概念、命題和規律為主要內容，其本身就具有高度的抽象性和概括性，因此，以核心素養為指導，探究初中學生數學概括能力的引導與培養策略具有重要的意義。

一、注重形象化教學，提升學生的數學概括能力

概念是培養學生概括能力的關鍵載體，而概念的獲得往往需要豐富而又典型的實例。因此，在具體教學實踐中，教師應最大限度地呈現出各種有利于概念抽象的感性背景材料，然后啟發和引導學生對其進行觀察、分析、抽象和概括，領略這些背景材料中的共同屬性，進而引導學生通過概括提升分離問題核心和實質的能力。

例如，在組織學生學習“中心對稱”概念時，教師可以結合日常生活場景呈現如中國移動通信標志、紙牌黑桃8、禁止停車標志等學生較為熟悉的圖形，然后引導學生仔細觀察，并通過“想一想他們之間有哪些共同之處”“能否利用所學‘圖形的旋轉知識提煉出共性”等方式啟發學生逐漸舍棄顏色、形狀、數量等方面的特性，進而幫助學生獲得中心對稱的概念和基本特征。

二、圍繞對比化教學，提升學生的數學概括能力

概括是促使學生從感性走向理性過程的關鍵，而初中學生的思維往往是構建在操作經驗和已學知識這一基礎之上的，因此，教師應最大限度地發揮知識正向遷移的作用，及時為學生提供與事物本質密切關聯的典型材料，然后以此為載體幫助學生通過概括提升區分本質與非本質屬性的能力。

例如，“二次函數”就是初中數學教學中一個重要的學習內容，這種重要性不僅體現在二次函數是函數知識的深化方面，更體現在函數概念構建過程中可以有效培養學生的抽象概括能力方面。但二次函數與一次函數、一元二次方程之間有著密切的聯系，因此，教師可以運用對比化教學模式，類比一次函數的抽象概括過程，以及一元二次方程根的判別式、韋達定理等思想方法，讓學生進行聯想和概括、總結，深度理解二次函數與一次函數、一元二次方程之間的聯系和區別，有效培養學生的函數思維。

三、強化串聯化教學，提升學生的數學概括能力

知識串聯化教學可以有效幫助學生將所學知識網絡化、系統化，也能夠提升學生的數學概括能力，因此，教師應強化知識的串聯意識，引導學生對已學知識進行相應的梳理，通過問題串的形式有效改變零散的知識狀態，進而幫助學生通過概括提升在各類現象之間建立聯系的能力。

例如，函數是初中數學中的核心概念，也是學生難以理解的知識點，因此，教師應強化學生對所學知識的梳理，從已學知識著手，創設如下問題串，引導學生概括出各個事例中兩個變量之間的關系，進而促使學生經歷函數概念的抽象和概括過程。

（1）已知某小車的平均行駛速度為40km/h，試求路程與時間的關系。

（2）試求某一地區某年溫度與時間的關系。

（3）已知某一正方體容器，試求該容器內溶液的體積與溶液深度之間的關系。

四、基于數學建模，提升學生的數學概括能力

數學建模與數學抽象和概括有著密切的聯系，可以認為是解決實際問題、提高學生概括能力的一種強有力手段，因此，在具體教學實踐中，教師應盡可能地在解題之后及時引導學生反思該題意在實際生活中的應用場景，促使學生在實際建模中提高概括意識，進而幫助學生通過概括提升把具體問題抽象為數學模型的能力。

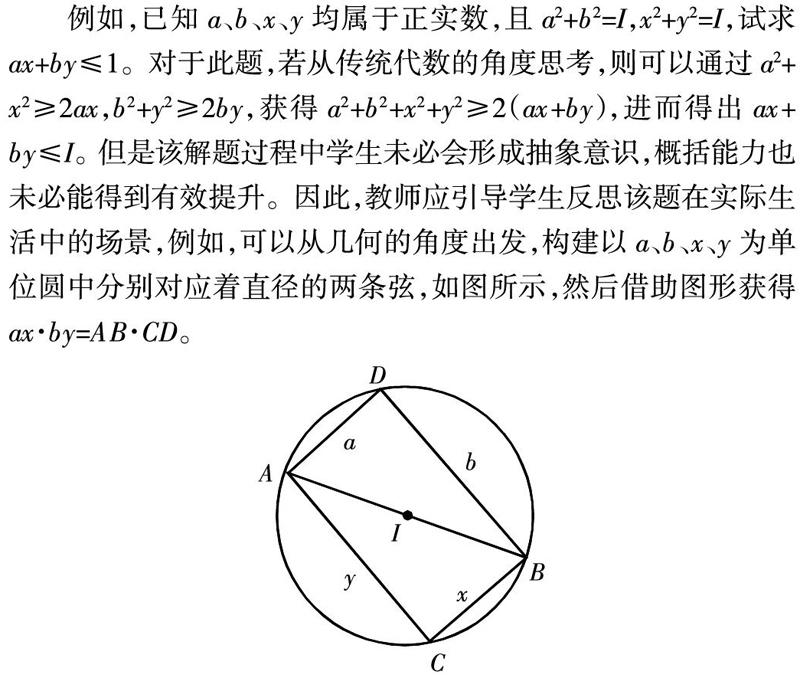
例如，已知a、b、x、y均屬于正實數，且a2+b2=I，x2+y2=I，試求ax+by≤1。對于此題，若從傳統代數的角度思考，則可以通過a2+x2≥2ax，b2+y2≥2by，獲得a2+b2+x2+y2≥2（ax+by），進而得出ax+by≤I。但是該解題過程中學生未必會形成抽象意識，概括能力也未必能得到有效提升。因此，教師應引導學生反思該題在實際生活中的場景，例如，可以從幾何的角度出發，構建以a、b、x、y為單位圓中分別對應著直徑的兩條弦，如圖所示，然后借助圖形獲得ax·by=AB·CD。

總之，數學教學中，教師應以生為本，在教學實踐中注重形象化、對比化、串聯化教學以及數學模型建構，注重知識的梳理和學習經驗的總結，進而達到培養學生概括能力和抽象思維的目的。

參考文獻：

[1]陳寶青，雒義霞.數學抽象及其教學實踐：基于數學抽象概括能力培養的視角[J].數學教學通訊，2020（27）：40-41.

[2]李樹棟.高中數學教學應注重培養學生的抽象概括能力[J].高考，2020（32）：31.