吸入式噴嘴的風速標定裝置的標定效果分析
陳栩穎
(上海海立電器有限公司,上海 201206)
0 引言
空氣流速是一個常用的測試參數。制冷暖通領域很多電器的性能測試都會用到該參數,如房間空氣調節器采用空氣焓差法測試制冷量時用到了風量這個空氣流速所對應計算值[1]。目前,空氣流速點風速主要的測量裝置是熱線風速儀、畢托管等。而風速測量設備在使用前都需要對其進行標定。風速標定的目的是對各風速儀的性能進行測試。
目前行業中普遍采用的風速計標定方法有兩種:一種是旋臂機法,此方法結構復雜,易擾動靜止的空氣,從而影響標定精度;另一種是相對標定法,此方法不易實現1.0 m/s 以下的低風速標定和校正,且畢托管本身標定也會帶來一定的誤差,另外,風速改變引起風管內速度場的不穩定也會對標定精度帶來影響。因此,如何方便快捷實現風速計在低風速的標定與校正,同時保證標定的精確度和準確度,是測試領域需要解決的問題[2]。參考壓差式風量測量的方法[3-8],該測量的方法是通過改變風機頻率大小,在風管中不同風速狀態下進行風速測量和裝置標定。該方法通常采用的裝置為壓差計和畢托管。如何保證測量的精確度和準確度是該測量方法的重要關注點。該方法在管內風速過大時,風速測量的誤差會增大,所以一般的實驗會控制風管內的風速在低速中進行。但風速進一步升高后,風管內風速以及標定的不確定度[9-13]研究較少。
本文研究了一種負壓的通過空氣流量轉化為點風速的風速標定裝置。并對該裝置標定的結果進行不確定度的計算從而檢驗該裝置標定的效果。
1 實驗方法及原理
1.1 實驗裝置
在用于實驗室測量風量的節流裝置中,噴嘴是目前國際上公認的一種準確而方便的裝置[14],其流量系數穩定,相對同流量的其他節流裝置,其阻力損失更小,因此越來越多應用在風量實驗系統中。配合各種差壓計或差壓變送器可測量管道中各種流體的流量。
基于吸入式噴嘴的風速標定裝置,即應用壓差式風量測量原理進行設計,裝置布置如圖1所示。
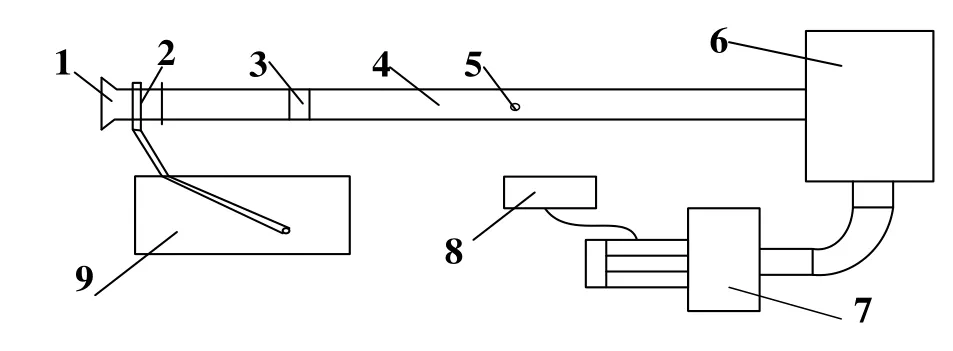
圖1 基于吸入式噴嘴的風速標定裝置
該裝置采用負壓吸入空氣,管道吸入噴嘴口處裝有壓力采集環,可通過壓差計測量管道內的平均風速。管中間設有風速計測孔,可以放入標準畢托管測量標準風管軸心風速大小。通過比對平均風速與標準畢托管軸心風速,獲得修正值,從而獲得該標定裝置的標定修正值,用于后續風速儀的標定使用。本次實驗所用的壓差計(U=0.016%,k=2)和畢托管U=0.3%)。
1.2 實驗方法
通過改變風機的頻率來調整風管內的風速大小。每個工況下,通過讀取標準流量管處的靜壓差及此時的大氣壓力、環境溫度來計算得出標準風道的風速。然后在風速計測孔中通過畢托管測量管道中心點處的風速,將不同工況下的標準畢托管測得的風速與管口處流量管所測風速計算值比較。
1.3 實驗原理分析
標準流量管是通過大氣壓力、空氣溫度、空氣相對濕度和某截面的壁面靜壓4 個參數測試流量[15]。裝置的實驗原理是用伯努利方程計算流量管流量,根據質量守恒定律,由標準流量獲得標準風道平均風速,再根據流體在管道內流動分布的特點,經標準畢托管測量風道軸心處的風速作為標準點風速,即風速計標定時的參照標準風速。
標準流量管所測的平均流速為:

式中,Δp1為壓差,Pa;ρ為被測空氣的密度,kg/m3,根據空氣溫度,大氣壓力計算得到[16]。
標準流量為:

式中,A1為標準流量管的喉部面積,m2;α為流量系數[16];ε為空氣膨脹系數[16-17]。
已知標準流量管的流量系數α與雷諾數Re[18]的對應數據:
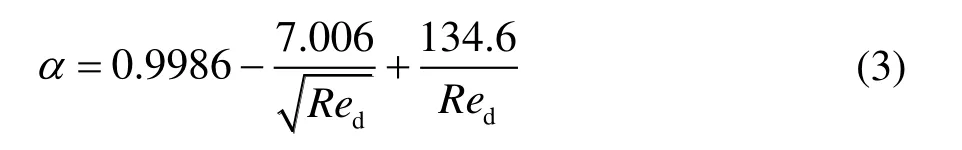
式中,Re為標準流量管喉部的雷諾數。
空氣膨脹系數ε與大氣壓和壓差相關,對于Δp≤2,000 Pa,空氣膨脹系數與兩者的關系式:

實驗時,所處環境的大氣壓力為103,080 Pa;標準風道內的雷諾數Re>2,300,屬于紊流狀態[19]。
通過質量守恒定律[20]:

式中,ρ1、ρ2為標準流量管喉部和標準風道空氣密度,kg/m3,兩者近乎相等;v2為標準風道的平均風速,m/s;A2為標準風道截面積,A2=A1。
由式(1)和式(5)可得:

標準風道的實際風速通過標準畢托管測量:

式中,Vm為標準風道軸心風速,m/s;K為畢托管系數,本次實驗,K=1;Δp2為壓差,Pa。
標準風道的平均風速與軸心風速之間的關系用β(修正值)表示:

1.4 實驗數據結果
該實驗分為4 個工況,各工況的實驗數據見表1。工況1、工況2、工況3 和工況4 的Re分別為34,968、66,858、90,995 和123,245。由表1 可知,風速的大小隨標準流量管喉部壓差的增大而增大。
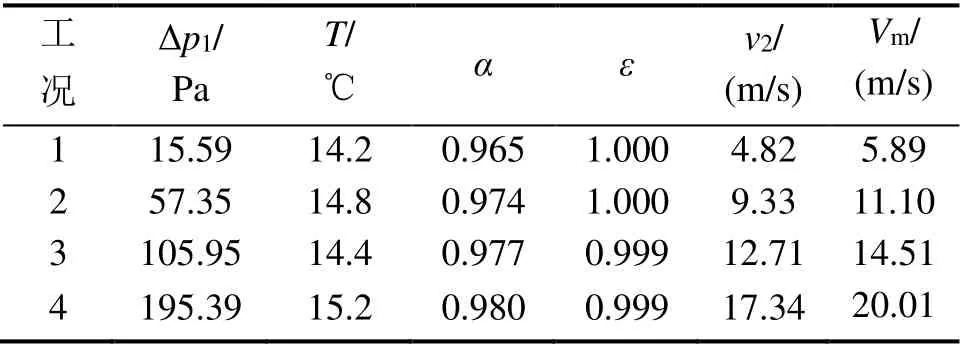
表1 不同雷諾數時實驗數據結果
2 標準不確定度評定
2.1 用標準畢托管測量風速帶來的不確定度u(Vm)
根據公式(7)得:
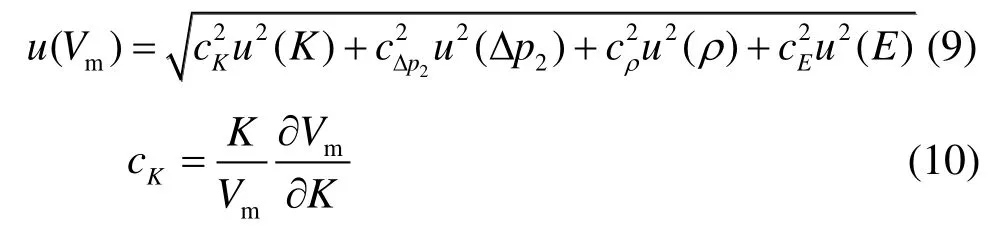
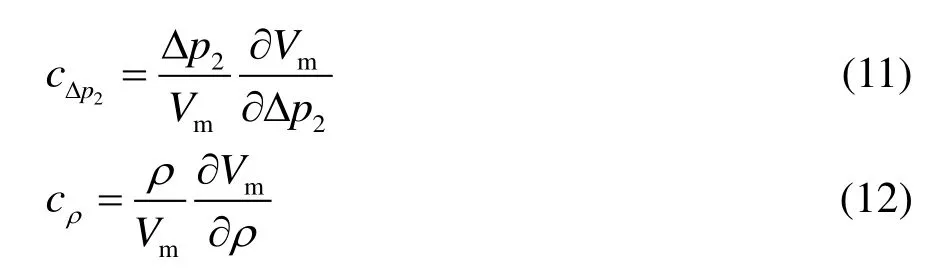
式中,E為重復性,cE=1;cK=1;cΔp2=0.5;cρ=-0.5。
畢托管的不確定度為U=0.3%(由標準給出):u(K)=0.3%/2=0.15%。
壓差變送器的不確定度u(Δp2)根據校準證書為U=0.016%,包含因子k=2,可得u(Δp2)=0.008%。
空氣的密度由氣體狀態方程計算可得:

式中,T為空氣溫度,K。

本次空氣溫度的測量采用儀器為二等標準水銀溫度計,溫度計的最小分度值為0.1 ℃,k=2,計算得到其不確定度u(T)=0.00009。
大氣壓的測量采用儀器為Delta 的HD2001 系列變送器,最大示值誤差為±50 Pa,k=2,計算得到其不確定度u(pa)=0.0002。
把u(T)和u(pa)帶入式(14)得出u(ρ)=0.057%。將u(Δp2)和u(ρ)的結果帶入式(9),得到各工況下,標準畢托管測量風速的不確定度,具體數據見表2。
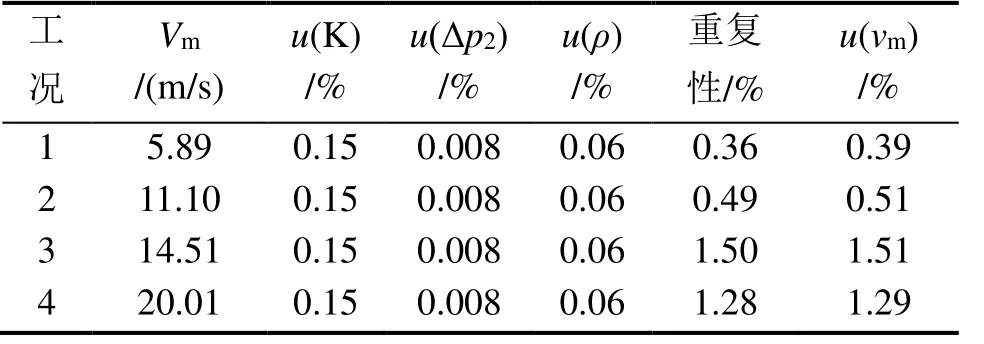
表2 不同雷諾數時標準畢托管測量風速的不確定度
由表2 可知,標準畢托管測量風速的不確定度基本隨著風速的增大而增大。在標準風速值大于14.51 m/s 時,該不確定度大于1%。
2.2 被檢標準風道平均風速的不確定度u(v2)
根據式(6)得:
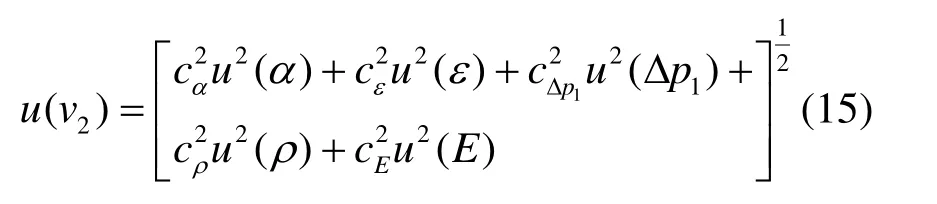
式中,cα=1;cε=1。
根據式(3)得α的不確定度:


已知雷諾數Re=v1d/υ,υ為空氣的動力黏度,可得雷諾數的不確定度為:
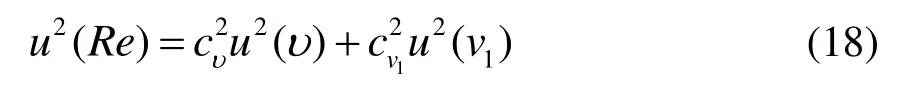
式中,cυ=-1;cv1=1。
α的不確定度,具體計算數據見表3。ε的不確定度約等于0,可忽略。
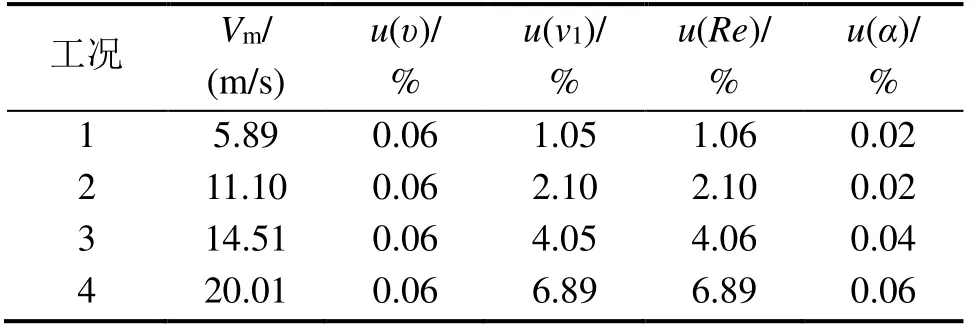
表3 不同雷諾數時α 的不確定度
將各數據帶入式(15),得到各工況下,被檢標準風道平均風速不確定度,具體數據見表4。由表4 可知,被檢標準風道的不確定度隨著風速的增大而增大,且增長的幅度越來越快。
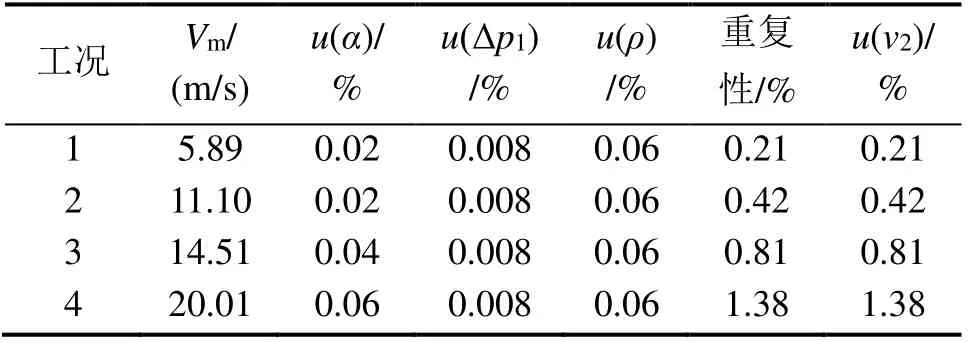
表4 不同雷諾數時被檢標準風道平均風速的不確定度
2.3 標準風道的平均風速與標準畢托管所測軸心風速比值β 的不確定度u(β)
通過式(8)可以得到β的不確定度為:

式中,mVc=1;2vc=-1。
根據式(19),可得到β的不確定度,具體數據見表5。由表5 可知,β的不確定度隨著風速的增大而增大。
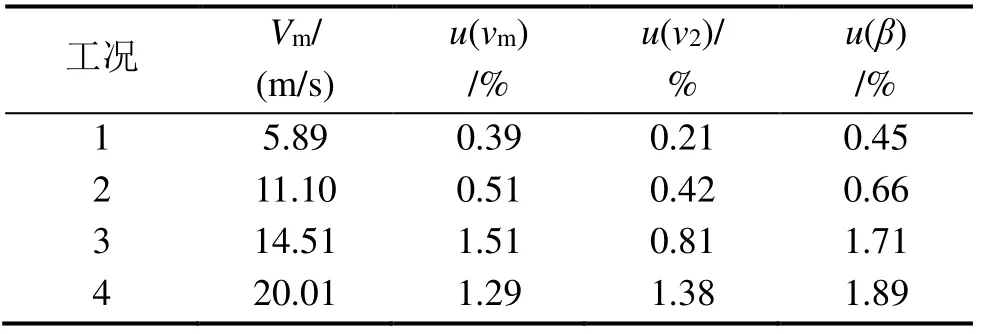
表5 不同雷諾數時β 的不確定度
3 實驗結果分析
標準風速為5.89 m/s 時,計算數據分析比較見圖2 和圖3。從圖2 可知,Vm和v2的不確定度受多種因素的影響,重復性、K、壓差和密度在該工況下對Vm的影響分別占84.7%、14.70%、0.01%和0.59%,重復性對Vm和v2的不確定度影響最大。
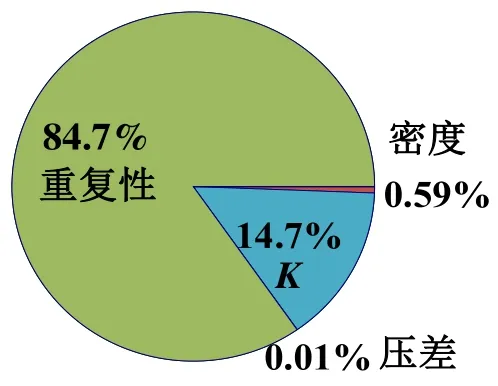
圖2 參數對Vm 不確定度的影響
由圖3 可知,β的不確定度隨著風道內風速的增大而增大。在標準風道內的軸心風速在11.10 m/s內時,β的不確定度變化緩慢不超過1%。在標準風道內的軸心風速在11.10~20.01 m/s,β的不確定度增長的幅度變大,值大于1%。
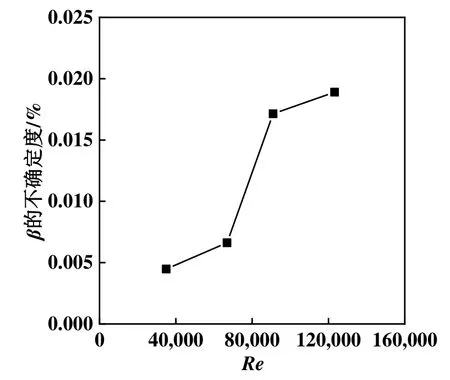
圖3 β 的不確定度隨雷諾數的變化
4 結論
本文研究了一種吸入式噴嘴的風速標定裝置通過將流量管轉化的風速與通過標準畢托管所測的軸心風速之間的對比,通過對實驗數據的處理分析,得到以下結論:
1)實驗風速的不確定度受重復性的影響最大,以標準風速為5.89 m/s 時Vm為例,重復性在該工況下對Vm的影響占84.7%;
2)隨著風道內風速的增大,風道內風速的不確定度的值基本呈上升趨勢;
3)通過流量管所測的標準風道的平均風速與標準畢托管所測軸心風速比值β(修正值)的不確定度隨著風道內風速的增加而增大,當風管內的風速超過一定值時,裝置標定的可靠性會下降;該風速標定裝置在11.10 m/s 以內數據可信賴性更高;
4)針對該裝置重復性不確定度占比大的情況,風道設計要合理,比如增加整流穩定裝置;要讓電壓穩定,變頻器控制平穩來保證電機運轉穩定;要在周圍沒有劇烈變化的環境下進行,防止周圍環境的干擾。

