不同管道內冰漿流動換熱特性及冰堵分析

張雪，劉圣春，宋麗瑩，徐智明

（天津商業大學機械工程學院，天津市制冷技術重點實驗室，天津 300134）

0 引言

隨著全球電力需求的增長，許多環境問題如全球變暖、臭氧層損耗等受到了廣泛關注，并嚴重影響全球能源政策[1]。為了緩解能源緊張，提高能源利用效率，儲能技術發揮著關鍵作用。冰漿是由冰晶、液態水和防凍劑組成的絮狀混合物，因其具有良好的流動特性和較大的能量密度，在同一運行工況下相較于傳統冷凍水冷卻能力高4 倍至5 倍[2-3]，已成為一種新型相變材料在蓄冷系統中被廣泛使用[4-8]。

目前，國內外學者對冰漿系統的研究較多。在換熱特性方面，JEAN-PIERRE 等[9]實驗研究了雙管換熱器中冰漿的換熱情況，結果表明，隨著含冰率的減小，傳熱系數先減小，在低含冰率時基本保持不變。趙騰磊等[10]以含冰率在20%以下的冰漿為模型進行實驗研究，分析冰漿的密度、導熱系數、比熱和動力黏度，結果表明冰漿的傳熱系數與含冰率成正比。張曼等[11]建立了動態冰漿傳熱特性的數理模型，數值研究了流速、管徑和冰漿體積分數對傳熱系數的影響。LEE 等[12]實驗研究了以冰漿作為冷卻介質的雙管換熱器，結果表明換熱率隨質量流量和含冰率的增加而增加，流速低時，冰粒對換熱的影響更為明顯。BELLAS 等[13]實驗研究了帶冰漿的板式換熱器的性能，得出當含冰率在5%～20%時，傳熱系數基本保持不變。LIU 等[14]數值研究了水平直管直徑、長度、含冰率和流速對冰漿流動壓降的影響，驗證了仿真模型的可靠性，進一步發展了黏度與流速的數學模型。簡夕忠等[15]數值研究了含冰率、流速、管徑和添加劑種類等因素對冰漿換熱效果的影響。由于冰漿系統涉及到相對比較復雜的流動及傳熱問題，目前，對冰漿傳熱特性的研究在理論分析、數值計算和推廣應用方面仍需完善。

本文利用顆粒動力學理論，通過數值模擬的方法得出冰漿在不同類型管道內的流動換熱特性，并對直管內冰堵現象進行了分析。

1 數學模型

在Fluent 軟件中采用雙歐拉流體模型，結合顆粒動力學理論建立數值模型的控制方程。

1.1 質量守恒方程

冰漿本質上為一種液固兩相混合流體，冰粒固體為直徑較小的顆粒，內置顆粒相模型，設兩相分別為q相和p相。

相位q的體積：

q相的有效密度按式(3)計算：

q相的連續性方程為：

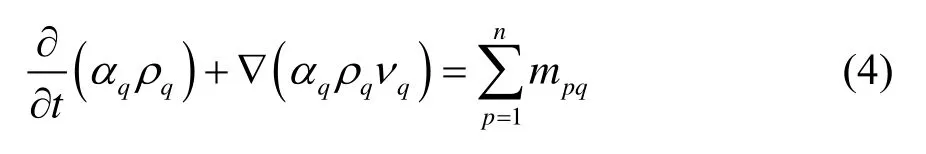
由質量守恒方程，得：

式中，αq為q相的體積分數；ρq為q相的密度，kg/m3；mpq為p相到q相的質量傳遞速率，kg/(m3·s)；vq為q相的速度，m/s。

1.2 動量守恒方程

將冰漿看作固液兩相流體，用液相動力參數描述動量方程[16]，可得：

式中，下標s 表示固相；l表示液相；vsl為固液兩相間的相對速度，若msl＞0，則vsl=vs；若msl＜0，則vsl=vl，且vsl=vls；τl為液相切應力，Pa；Fl為外部體積力，N；Flift,l為升力，N；FVm,l為虛擬質量力，N；Ksl為固液相間的動量交換系數。

固體顆粒相動量方程為：

液相與固體顆粒相之間的作用力可采用GIDASPOW[17]模型確定。

當αl＞0.8 時，固-液動量交換系數Ksl為：

當αl≤0.8 時，Ksl有如下形式：

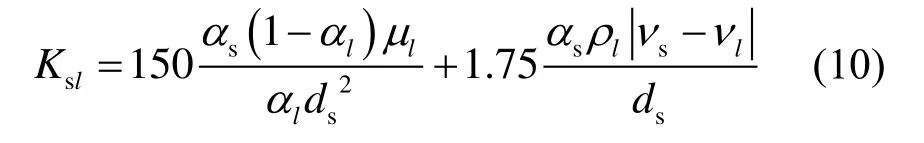
式中，Re為相對雷諾數；ds為顆粒直徑，m。

q相和p相的相對雷諾數為：

1.3 能量方程

能量控制方程[18]如下：

式中，λeff為冰漿的有效導熱系數，W/(m·K)；ST為源項，W/m3。

1.4 湍流方程

選擇k-ε湍流模型，考慮固液兩相間的相互作用[16]：

式中，C1ε=1.44；C2ε=1.92；σε=1.3；σk=1；μt,m=ρmCμk2/ε；Cμ=0.09；下標m為固液混合相；k為湍流脈動動能，J；ε為湍流脈動動能耗散率；μt,m為混合相湍流動力黏度，kg/(m·s)；σk為湍流脈動動能普朗特數。

1.5 黏度模型

冰漿是一種固液兩相混合物，物理密度、動力黏度以及結冰點不僅與受添加物體積分數影響，還與含冰率有關，THOMAS[19]通過反復實驗和理論推算，得出黏度關于含冰率的公式：

式中，φi為含冰率，%。

1.6 相變模型

在冰漿換熱特性模擬過程中，開啟能量方程，將冰-水換熱模擬寫入相變UDF 程序中，收斂精度設為10-4。

2 數值模擬模型圖及邊界條件設置

2.1 管道模型

90°彎管和T 型管模型分別如圖1(a)和圖1(b)所示。管道直徑為0.02 m，管總長為1 m，彎管和T 型管均在中間位置處發生改變，彎管曲率半徑為0.1 m，網格質量在0.7 以上，管道分流處采用結構化網格形式。溶液進出口位置及重力方向見圖1。

圖1 90°彎管和T 型管管道網格劃分模型

2.2 邊界條件設置

對冰漿在90°彎管、T 型管內的換熱特性進行模擬。具體參數設置為：含冰率IPF 為5%～25%，流速為0.2～1.5 m/s。冰粒直徑約為10-4m。邊界條件設為速度入口，出口設為出流，壁面設為無滑移，采用定壁溫條件，溫度為1 ℃；入口處冰相和水相的溫度均為0 ℃；湍流模型選用k-ε模型。冰漿兩相流體的物性參數如表1所示。

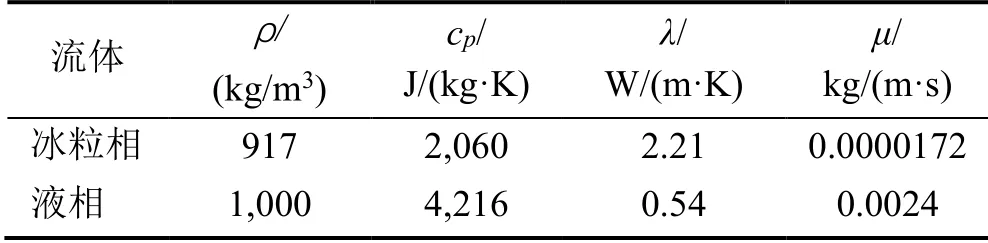
表1 冰漿兩相流體的物性參數[20]

3 數值模擬結果分析

3.1 90°彎管內冰漿換熱特性結果分析

圖2 和圖3所示為含冰率為10%時，90°彎管截面上溶液平均溫度分布和焓值分布。由圖2 和圖3 可知，縱截面上，溶液平均溫度變化較小，保持在0～1 ℃，彎管處溶液焓值最大為2.46×104J/kg。

圖2 90°彎管截面上溶液平均溫度分布

圖3 90°彎管截面上溶液的焓值分布

圖4所示為90°彎管截面上流體流動的速度分布。由圖4 可知，在90°彎管中，流體流動速度從入口處逐漸增大直至彎管處達到最大，約為1 m/s，經過轉彎處，出現明顯分層現象，在離心力的作用下，冰粒靠近管外側速度明顯大于內側，逐漸在外側堆積，這與文獻[21]的結果相符。

圖4 90°彎管截面上流動速度分布

綜合以上分析，在90°彎管處，由于存在摩擦和二次流現象[22]，冰漿流體流動阻力大，擾動強烈，摩擦損失加大。而流速從入口處逐漸增大，在彎曲處流速最大且開始出現分層現象，在流速較大區域，冰-水換熱效果緩慢，冰粒不易完全融化[23]。因此，溶液平均溫度隨流速增大而升高，在彎曲處溫度高于入口處，且冰的密度略小于水，由于受到浮升力作用和彎管處冰漿流速較快的影響，冰粒在流體的帶動下，逐漸沿著管壁一側分散開來。經過彎曲處，平均流速減小，溫度稍降低。溶液溫度分布從大到小依次為彎曲處、出口處和入口處，但總體溫度比較均勻。

3.2 T 型管內冰漿換熱特性結果分析

含冰率為10%時，T 型管縱截面處冰粒焓值分布，如圖5所示。

圖5 T 型管縱截面冰粒焓值分布

由圖5 可知，入口處溶液的焓值較高，隨著管道流動呈梯形下降趨勢，在分流處焓值減小。這是由于冰漿在管內流動中，摩擦損失和紊流效應使能量損失。在交叉處，擾動強烈，液態水與冰粒之間交換動量。分流之后固液兩相流動趨于穩定，在出口處壓力再次降低。

3.3 直管內冰漿流動冰堵分析

為了解決冰漿堵塞造成換熱效果差這一問題，對直管中冰漿的分布進行數值模擬。管道直徑為0.02 m；入口邊界條件為速度型，出口為出流型。重力方向為Y軸負方向。當含冰率為20%，取管道中間橫截面位置進行分析，得到冰粒的體積分數分布結果如圖6所示。可以分為低體積分數區、高體積分數區和過渡區。圖7所示為文獻[24]中的3 種冰漿的流動流態。

圖6 不同流速下冰粒在直管橫截面上體積分數分布

圖7 文獻[24]中3 種冰漿流動流態

由圖6(a)和圖6(b)可知，當流速為0.2 m/s 和0.3 m/s 時，冰粒體積分布分層明顯，上層冰粒體積分數最高約為0.4，底部冰粒體積分數最低，幾乎為0，中間為過渡區，這與圖7(a)對應，由于流速較小，在高體積分數區黏滯力較大，使冰層沉積，管道堵塞。過渡區流速較高、體積分數區大，小于臨界沉積速度，仍有可能造成冰堵。當流速為1 m/s時，由圖6(c)可知，冰粒體積分數分布整體較為均勻，上層為移動床流動，下層為非均質流動，即懸浮床流動，與圖7(b)對應。當流速大于1.5 m/s 后，如圖6(d)和圖6(e)所示，此時，流速大于臨界沉積速度，整個管道內呈現為懸浮床模型，冰粒速度相當，體積分數分布均勻，與圖7(c)相對應，發生冰堵情況較少。

通過對不同流速下的冰粒體積分數模擬結果的比較，選擇1.5 m/s 作為冰漿由移動床流動變為懸浮床流動的第二臨界流速，冰粒分布趨于最均勻。

不同含冰率條件下，冰漿體積分數的最值與流速的關系如圖8所示。由圖8 可知，隨著含冰率的增加，A 點的第一臨界速度逐漸減小，在1～2 m/s之間，C 點的第二臨界速度減小，在10 m/s 左右。其原因是含冰率增加對湍流效應的影響大于對黏性摩擦的影響，因此，含冰率高的冰漿更有可能在較低流速下轉化為均勻流，減少冰堵發生。根據固體冰的分布輪廓，冰漿的總體積為：

圖8 不同含冰率條件下冰漿體積分數最大值（最小值）隨流速的變化

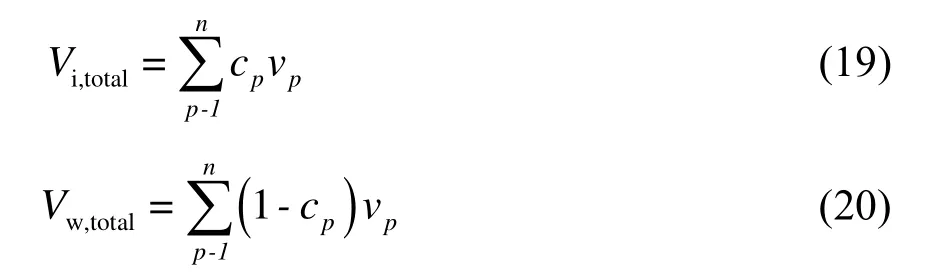
4 結論

本文利用Fluent 軟件對冰粒在不同管道（90°彎管和T 型管）內的換熱特性和直管內分布情況進行理論分析，得出如下結論：

1）當管徑為0.02 m、管總長為1 m 時，在90°彎管處，冰粒出現速度分層現象，管外側速度大于內側；冰漿溫度在彎曲處最大，在出口處，溫度略有降低，但整體溫度分布均勻；T 型管內溶液總焓值持續降低，經過分流處后，焓值降低更加劇烈，能量損失明顯；

2）對冰堵風險的預測結果表明，當直管管徑為0.02 m、管長為1 m、流速大于1.5 m/s 時，流態為懸浮床流，冰粒體積分數分布均勻，冰堵風險低；

3）當直管管徑為0.02 m、管長為1 m 時，得出冰漿最大值體積分數、最小值體積分數與流速之間的變化曲線，第一臨界速度和第二臨界速度分別為1～2 m/s 和10 m/s 左右，兩者均隨含冰率的增加而減小，含冰率高的冰漿更有可能在較低流速下轉化為均勻流，減少冰堵發生。