船舶推進軸系動力學縮比模型設計

周凌波，熊晨熙，段 勇，吳江海，孫玉東，魏 強，2

（1.中國船舶科學研究中心船舶振動噪聲重點實驗室，江蘇無錫 214082；2.中國艦船研究設計中心，武漢 430064）

0 引 言

船舶推進軸系的作用是將主機的功率傳遞到螺旋槳，并將螺旋槳的推力傳遞到船體，推動船舶前進。在船舶推進軸系的三大振動問題——扭轉振動、縱向振動和回旋振動中，回旋振動是最為突出的一個難題，關于它的研究，相對于扭轉振動和縱向振動的研究來說，不論是在文獻發(fā)表的數量上還是在研究深度上都是最不夠的[1]。水面船舶推進軸系的回旋振動作為造成推進軸系故障的主要原因之一，不僅會嚴重影響推進軸系的正常運轉，導致推進軸系零部件的異常磨損和疲勞破壞，更會激起艉部船體結構的異常振動，產生顯著的水下低頻、多頻強線譜輻射噪聲，大大影響水面船舶的聲隱身性能[2]。

對于推進軸系回旋振動動力學特性及其控制方法的研究，基于經費、維護和技術上的掣肘，多數僅停留在數值和仿真計算階段，缺乏有效的試驗驗證。因此，建造與實船軸系相匹配的縮比軸系回旋振動試驗模型，將理論和數值分析與試驗測試相結合，顯得尤為重要。對于工業(yè)轉子-軸承系統，國內對其縮比模型及縮比關系已經開展了一定程度的研究[3-5]。船舶推進軸系與工業(yè)轉子系統雖然具有一定的相似性，但兩者的安裝基礎條件有區(qū)別：工業(yè)轉子系統多安裝在剛性基礎上，而船舶的推進軸系則是安裝在船體結構上。船體結構屬于一種彈性支撐，其對于軸系的動力學影響不可忽略。因此，在對船舶推進軸系進行動力學縮比設計時，不僅需要像工業(yè)轉子一樣考慮轉軸、軸承、軸承基座的動力學影響，還需要進一步計入船體支撐結構的動力學影響。

本文以某型水面雙體船及其推進軸系為原型，計入船體結構的支撐動力學影響，依據動力學參數的縮比換算關系，設計了一種驗證軸系回旋振動控制技術的陸上縮比軸系試驗模型。然后通過對實船推進軸系和縮比軸系模型的動力學仿真分析和對比，驗證了所設計縮比軸系的動力學適用性，為軸系回旋振動控制方法的驗證提供了有效的試驗對象。

1 縮比換算關系和軸承剛度估算公式

1.1 縮比換算關系

通常設計縮比模型，幾何縮比Kl、材料的彈性模型縮比KE和密度縮比Kρ是確定的，因此用這三個基本量可以推導出其他物理量的縮比關系[3]，整理列入表1。

表1 縮比模型與原型各物理量間的縮比關系Tab.1 Relationship between the scaled model and the prototype

1.2 軸承剛度計算公式

（1）賽龍軸瓦剛度計算公式為

式中，K1為賽龍軸瓦剛度，E0為壓縮模量，L為軸瓦長度，D為軸承直徑，t為壁厚。

（2）深溝球軸承徑向剛度計算公式為

式中，K2為徑向剛度，φ為滾珠直徑，F為徑向載荷，N為滾子個數，α為接觸角。

（3）圓柱滾子軸承徑向剛度計算公式為

式中，K3為徑向剛度，P為徑向載荷，Z為滾子個數，l為滾子有效長度，β為接觸角。

2 實船及其推進軸系原型

2.1 設計原型

設計原型以圖1所示的某型水面雙體船的推進軸系為對象，其船長約為54 m，排水量約為1 400 t。該船推進軸系如圖2所示，分為艉軸、中間軸、推力軸三段，總長為15 568 mm，材料為鍛鋼。其中，艉軸長為8 000 mm，直徑為200 mm；中間軸長為4 338 mm，直徑為180 mm；推力軸長為3 230 mm，直徑為200 mm。艉軸與中間軸之間為套筒式液壓聯軸器，質量為135 kg；中間軸與推力軸之間為法蘭式液壓聯軸器，質量為143 kg。螺旋槳為6 葉定距槳，材料為鎳鋁青銅，槳葉和槳轂總質量為1 420.3 kg，轉動慣量為363.3 kg·m2。

圖1 某型水面雙體船Fig.1 Surface catamaran

圖2 推進軸系結構組成Fig.2 Structural composition of propulsion shafting

2.2 全船有限元模型

建立的全船有限元模型如圖3 所示。船體大部采用板單元建模，轉軸與艙室支柱使用梁單元建模，螺旋槳使用三維實體單元建模。主甲板、下甲板和底部船體分段中，T 型加強肋的腹板使用板單元，面板使用梁單元，球扁鋼和角鋼加強肋統一簡化為角鋼并用梁單元模擬；主甲板以上船體結構的加強肋則都使用梁單元模擬。船體結構中的煙囪分段、甲板上舷墻分段、穩(wěn)定鰭加強裝置、舭龍骨，導流罩和焊縫等都以分布質量的形式表達。基座部分中位于潛體中的推進電機基座、推力軸承基座、中間軸承基座等按照圖紙詳細建模，其它沒有建模的基座則將其重量分攤到相應的船體主結構上。船上設備，包括油艙和水艙中的質量、發(fā)電機組、推進電機、軸承、變壓器、變頻器、吊架、錨鏈、前后鰭、舵桿舵葉、交通艇、通風排氣系統、鍋爐、輪機設備、應急發(fā)電機、食品、蓄電池、泵、空調、桅檣等設備的質量，都按照重心加載在給定位置上或者按照質量均勻分布在艙壁上。船上的其它質量，如電纜、油漆等，則按照肋位分布在相應的船體結構上。

圖3 全船有限元模型Fig.3 Finite element model of the whole ship

推進軸系通過艉后軸承、艉前軸承、中間軸承和推力軸承基座與艇體連接。槳轂內表面與轉軸采用剛性耦合。螺旋槳采用二次實體單元模擬，軸段采用梁單元模擬，艉后軸承、艉前軸承和中間軸承采用水平和垂向的彈簧單元與船體連接。推力軸承對軸系的縱向運動及橫向運動同時具有約束作用，因此在縱向及橫向分別采用水平、垂向與縱向的彈簧單元進行模擬。推力盤、聯軸器與彈性聯軸器則都采用點質量進行模擬。

所建立的船體和推進軸系有限元動力學模型已經過實船航行振動試驗的對比驗證，兩者的動力學特性具有較好的一致性[6]。

2.3 軸承支撐剛度計算

艉后軸承和艉前軸承都屬于水潤滑動壓滑動軸承，軸瓦為賽龍材料。兩者對軸系的徑向支撐剛度由潤滑膜剛度、軸瓦剛度和安裝位置的船體剛度三者串聯而成[7]。其中，潤滑膜剛度采用流體動壓潤滑理論[8]計算，賽龍軸瓦的剛度根據公式（1）進行計算，其軸承負荷以及安裝位置的船體剛度采用有限元法計算。

中間軸承為大比壓自潤滑白合金軸承，軸承剛度采用CB/Z 208[9]中的推薦值，其軸承負荷以及安裝位置的船體剛度采用有限元法計算。

推力軸承的徑向支撐部分為雙列圓柱滾子軸承，軸承剛度采用公式（3）進行計算，其軸承負荷以及安裝位置的船體剛度采用有限元法計算。

各軸承徑向負荷、船體基座剛度及總支撐剛度的計算結果如表2、圖4和表3所示。

表2 實船各軸承的徑向負荷Tab.2 Radial load of each bearing of the real ship

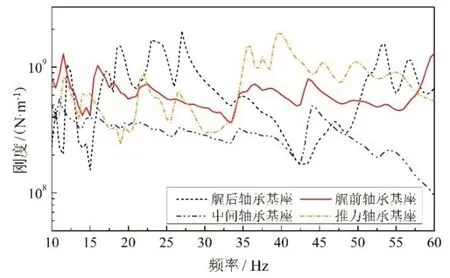
圖4 各軸承安裝位置處的船體基座剛度Fig.4 Hull base stiffness at each bearing position

表3 實船軸系支撐剛度Tab.3 Support stiffness of the real ship’s shafting

3 縮比軸系模型設計

由于縮比軸系試驗模型為在實驗室中用于驗證回旋振動控制新方法有效性的原理性試驗驗證模型，因此縮比模型要求設計簡單，能反映基本的物理現象，大小滿足實驗室場地及設備安裝要求即可。綜合考慮實驗室的安裝測試條件以及項目的研究經費和研究周期等要求，軸系縮比模型的結構尺寸采用縮尺比例1:4進行設計，并選用密度和彈性模量相近的結構材料，但考慮到實際加工因素，并不要求所有的機械細節(jié)參數嚴格滿足縮比要求。

縮比軸系模型的組成主要包括：3 段轉軸、4 個支撐軸承、1 個螺旋槳模擬質量盤、2 個剛性聯軸器、1個彈性聯軸器、1臺驅動電機、軸承基座及其他附件等結構。參照實船的布置形式，3段轉軸采用剛性聯軸器進行連接，艏端與電機輸出軸采用高彈性聯軸器進行連接。軸系采用4個徑向支撐軸承，分別對應實船軸系的后軸承、前軸承、中間軸承以及推力軸承徑向支撐。軸系采用直線校中方式進行連接，各軸段的長度、各軸承支撐中心的位置按照實船軸系進行縮比確定，尺寸參數如圖5所示。

圖5 縮比軸系支撐軸承及聯軸器位置Fig.5 Positions of the supporting bearings and couplings of the scaled shafting

本縮比軸系模型主要用于軸系回旋振動控制方法的研究，只產生少量的軸向靜態(tài)和動態(tài)載荷（主要為驅動電機輸出軸的軸向竄動力），所以縮比軸系中原推力軸承處主要承受徑向載荷，幾乎不承受軸向載荷。另外考慮到互換性以及計算和加工方便，支撐軸承均采用同一型號的深溝球軸承。同時考慮到后期控制裝置的施加方便，軸承外圈應盡量小。綜上考慮，軸承1～4統一選用HRB品牌6011型號的深溝球軸承，其外形及內部的尺寸結構如表4所示。

表4 HRB-6011軸承尺寸參數Tab.4 Parameters of HRB-6011 bearing

采用公式（2）計算各位置軸承處的徑向剛度，如表5所示。

表5 縮比軸系各軸承的徑向剛度Tab.5 Radial stiffness of each bearing of the scaled shafting

4 縮比軸系和實船軸系動力學仿真對比

分別計算縮比軸系和實船軸系的結構質量、軸承負荷、軸承剛度、橫向振動模態(tài)頻率和加速度傳遞函數（激勵點位于螺旋槳質心處），再根據縮比關系將縮比軸系的計算結果換算為對應實尺度時的結果，并在考核頻段10～60 Hz內與實船軸系的計算結果進行對比，如表6～9和圖6～8所示。

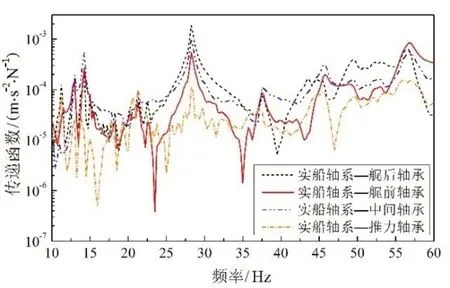
圖6 實船軸系各軸承位置處的傳遞特性Fig.6 Transmission characteristics of the real ship’s bearings

表6 尺寸和結構質量對比Tab.6 Comparison of the dimensions and structural masses

由表6和表7可見，縮比軸系換算后的尺寸與實船軸系一致，結構質量與實船軸系相比最大相差1.10%，軸承負載質量與實船軸系相比最大相差2.12%；由表8 可見，縮比軸系換算后的軸承支撐剛度與實船軸系相比，均處于合理范圍內；由表9 可見，縮比軸系換算后的低階彎曲模態(tài)頻率與實船軸系相比，最大相差4.93%。

表7 軸承負載質量對比Tab.7 Comparison of the bearings’masses

表8 軸承剛度對比Tab.8 Comparison of the bearings’stiffnesses

表9 軸系前3階橫向和垂向模態(tài)頻率對比（換算后）Tab.9 Comparison of the first three lateral and vertical bending modes of the shafting(after conversion)

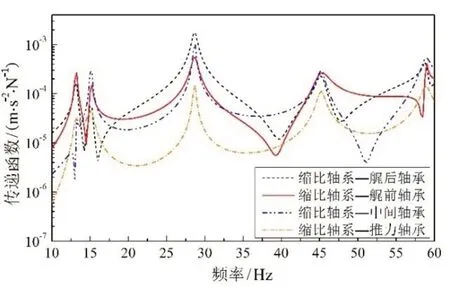
圖7 縮比軸系各軸承位置處的傳遞特性（換算后）Fig.7 Transmission characteristics of the scaled model’s bearings(after conversion)

由圖8 可見，縮比軸系在艉后軸承、艉前軸承、中間軸承以及推力軸承處換算后的動力學傳遞特性與實船軸系的趨勢基本一致，吻合度良好。

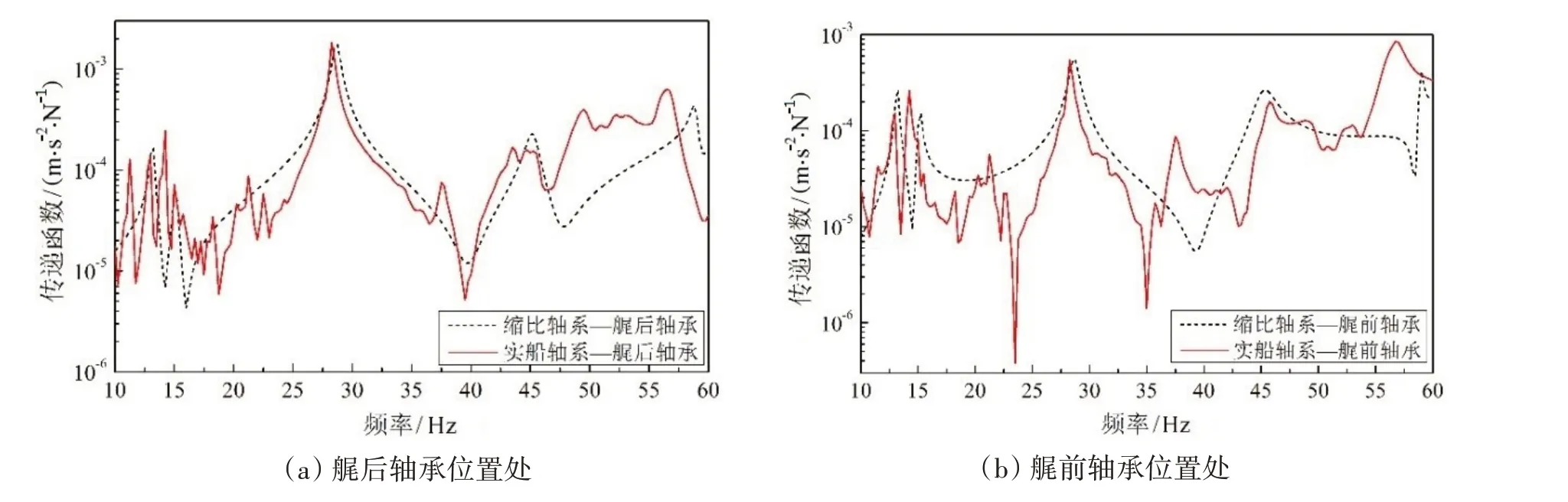
圖8 縮比軸系與實船軸系的傳遞函數對比（換算后）Fig.8 Comparison of the shafting transmission characteristics between the real ship and the scaled model（after conversion）

5 結 語

本文以某型水面雙體船及其推進軸系為對象，設計了一種實驗室陸上縮比軸系試驗模型，并對實尺度模型和縮比模型的動力學特性進行了仿真分析和對比，驗證了縮比模型的動力學適用性。由仿真計算結果對比可見，縮比軸系換算后的軸承負載質量與實船軸系相比，最大相差2.12%；縮比軸系換算后的軸承支撐剛度與實船軸系相比，均處于合理范圍內；縮比軸系換算后的低階彎曲模態(tài)頻率與實船軸系相比，最大相差4.93%；縮比軸系在艉后軸承、艉前軸承、中間軸承以及推力軸承處的傳遞規(guī)律與實船軸系的趨勢基本一致，吻合度良好。

因為實船的船體結構和軸系結構較縮比軸系復雜許多，除了軸系自身振動模態(tài)的參與外，還有許多的船體結構局部振動模態(tài)和耦合振動模態(tài)參與動力學傳遞，因此實船軸系的傳遞頻點較縮比軸系豐富，動力學傳遞特性也較縮比軸系復雜，很難實現完全一致。同時，受限于實驗室場地條件和其它客觀因素，縮比軸系在設計時做了一定的合理簡化（如并不附加船體結構、將螺旋槳簡化為質量圓盤、將滑動軸承簡化為滾動軸承等），因此其動力學特性與實船并不完全一致。但由文中動力學對比結果可見，兩者在考核頻段內的動力學傳遞特性吻合度良好，所以認為設計的該縮比軸系能夠滿足使用要求。