船舶避碰的粒子群-遺傳（PSO-GA）的混合優化算法研究

周鳳杰

（重慶青年職業技術學院，重慶 400712）

0 引 言

隨著世界各國之間貿易往來越來越頻繁，船舶海上運輸已經成為一種國際性的運輸產業，目前全世界大多數國家大宗進出口貨物都在使用海上運輸，海運航線極為繁忙。同時隨著海上科技的發展，船舶噸位越來越大，船速也越來越快，加大了海上碰撞事故發生的可能性。為避免船舶發生碰撞，船舶避碰決策研究已成為航海界關注的重要議題[1-3]。一直以來，許多專家學者都在發表有關避碰自動化、人工智能化的研究成果，目的就是為了避免或減少船舶在海上交通流量大與交通形式復雜情況下發生碰撞事故。經過多年的發展，該領域里的研究已逐步從傳統的基于數學理論的分析轉變為具有智能化以及學科多樣性的路徑規劃分析，相關領域的學術研究成果也在不斷豐富[4-6]。

以模糊邏輯算法為基礎，針對船舶碰撞危險度方面，通過計算機模擬的方法，給出了船舶航行避碰操作的決策模型。也有學者針對船舶碰撞危險度進行評估，利用模糊理論得到學習樣本，以每個目標的DCPA（Distance of the Closest Point of Approach）和TCPA（Time to the Closest Point of Approach）作為輸入，船舶碰撞危險指標作為輸出，并應用倒傳遞神經網絡進行多屬性決策[7-8]。除了進行船舶避碰的安全決策外，有學者還針對船舶避碰決策中的船舶運動態勢和避碰時機，應用灰色理論預測模型，以最近會遇距離及時間為預測參數，實際預測各目標與相對船舶之間在下一刻的運動方向[9-10]。近年來，研究學者開始將人工智能技術引入到避碰領域，利用類神經網絡、模糊理論及遺傳算法等來進行避碰問題的研究，進而開啟了有別于純數學模式的軟件計算自動避碰研究領域。同時針對海上近距離遭遇的船舶，有學者提出避碰技術及路徑規劃發展分析，以多目標優化算法搜尋最佳航線的路線規劃[11-13]。

綜合以上研究可以發現，目前關于船舶避碰的研究已經從數學模式進入到系統化模式，從專家系統進入到模糊神經網絡及人工智能與決策支持系統，各方面均獲得了較有價值的數學模型。但目前針對船舶避碰決策的路徑規劃研究，大部分是基于檢測算法視角，同時采用的優化算法存在收斂過早等問題。為此，本研究在粒子群算法及遺傳算法的基礎上，建立了船舶避碰路徑規劃模型，并選用仿真案例進行了驗證，克服了優化算法收斂過早等問題，以期為上述避碰決策提供科學合理的理論支持。

1 船舶避碰路徑分析

綜合文獻分析可知[14]，避讓船在船舶領域被侵犯前，就已經開始采取避讓行動。船舶領域為安全距離的集合，故采取行動后與直行船舶間的最小距離為船舶領域。但因航向資料跳動頻繁，本研究依據避讓行為的階段性特征，改以兩船間最近距離點C為中心，并將最近點前后固定時間區域分成三段（如圖1 所示）：AB段為發現危險區域段，此時還維持原航向，定義為初始航向；BD段為船舶施展避讓動作區域段，定義為避讓航向；待他船安全通過后，即在D點回復原航向，將DE段定義為回復航向。當BD段與AB段平均航向差值大于10°，且AB段與DE段誤差在3°以內時，即表示有采取避讓動作。

從圖1 的船舶避碰路徑圖解中可以看到，與他船最近距離點C前后固定時間內的航向是避碰路徑的新航向。為了確定避讓的航向以及避讓的DCPA 及TCPA，本研究在此取C點前后各2 min 內的航向值做平均；取原航向AB段的避碰動作時間點前的航向值做平均；在回復原航向DE段，因回復時間會較前段采取避讓動作時間短，故其航向平均時間的選取可比整段避碰時間區域短。

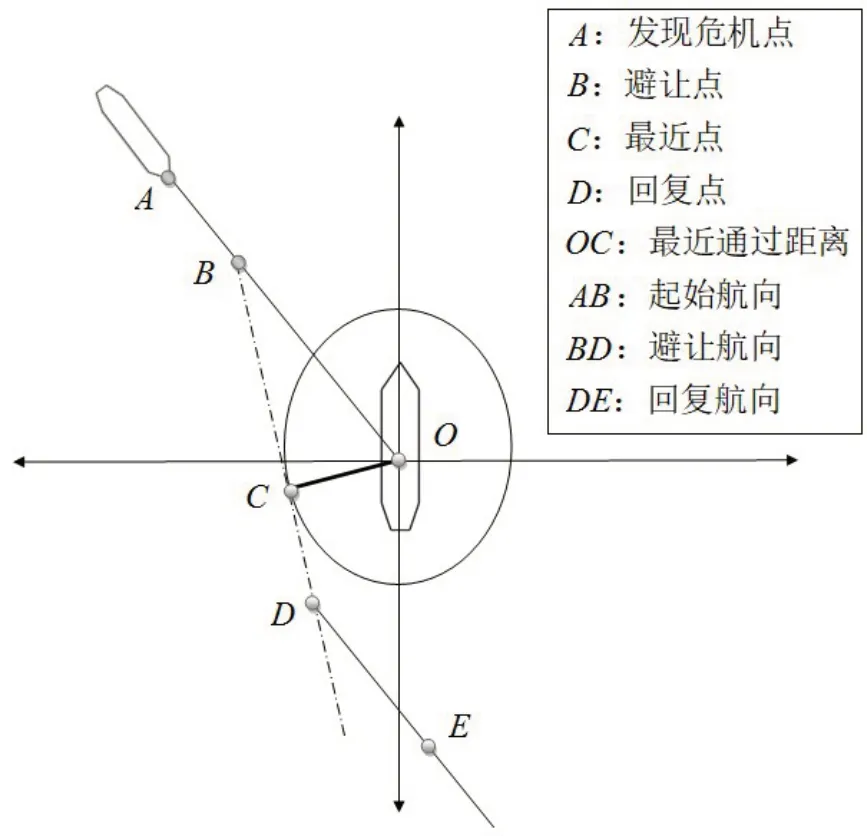
圖1 船舶的避碰路徑分析Fig.1 Analysis of ship’s collision avoidance path

2 船舶碰撞的條件判定

本系統以用戶所設定的DCPA 和TCPA 數值，作為判斷是否有碰撞危險以及何時開始執行避碰措施的依據。當兩艘船只目前的DCPA 值小于使用者所設定的DCPA 值，且TCPA 大于零時，表示兩船繼續依此航向前進，否則會有碰撞危險。在有碰撞危機的情況下，當兩艘船目前的TCPA 值開始小于使用者所設定的TCPA 值時，開始執行避碰措施。當兩艘船目前的TCPA 值開始小于零時，表示已離開兩船間的最接近點，無碰撞危險。根據圖1 中的船舶避碰路徑分析示意圖給出船舶碰撞危險判定條件，如表1所示。

表1 船舶碰撞危險度判定條件Tab.1 Determination conditions of ship collision risk

3 船舶避碰算法研究

3.1 PSO算法與GA算法概述

粒子群優化算法（Particle Swarm Optimization,PSO）其主要概念源自于動物群體行為理論，啟發于對鳥群及魚群集體行動的觀察，它們集體行動時通過個體之間特殊傳遞信息的方式，使整個團體能夠朝同一方向前進，由此尋求群體最大利益。其算法首先產生初始粒子群，每個粒子都為問題的一個解。而在粒子群搜尋空間中，每個粒子皆有自己的速度，并根據既往經驗及群體行為進行演化及修正，逐漸趨近最優解[15]。遺傳算法（Genetic Algorithm，GA）是基于生物遺傳演化的概念提出的一種優化算法，遺傳算法將這樣的概念隨機選取，接著用隨機的突變進化方式來優化所要的條件，作為對船舶碰撞的判斷依據。這種方法能夠更有效地在一個已知的空間范圍內去搜尋新的優化問題，并能尋求最優解。其核心原理就是達爾文所提出的進化論，適者生存，不適者淘汰[16]。

粒子群優化（PSO）算法雖然收斂速度快，但PSO 求解優化時，所有粒子在搜尋時向擁有最佳適應值的粒子方向移動，導致粒子的多樣性逐漸降低，而使粒子常常無法跳脫局部最佳解。因此學者提出了動態粒子群優化算法結合遺傳算法（PSO-GA），在粒子群求解最優解的過程中結合遺傳算法，在符合了特定條件的情況下，將粒子及其位移速度復制并投入交配池中，以交配、突變等機制作為干擾，使粒子能夠脫離局部最佳解，而得到全局的最佳解，此混合算法比起傳統粒子群算法具有更快的收斂速度，并獲得良好的分群質量。在考慮上述兩種算法優缺點的基礎上整合多目標優化求解，從而能夠快速搜尋且脫離局部最佳解，構建和優化船舶路徑，避免船舶碰撞。

3.2 避碰路徑的編碼及初始化

在船舶的避碰路徑上，為了獲得船舶避讓的TCPA 及DCPA 等關鍵信息，需要實時獲得環境信息，來更新船舶的位置及避碰路徑的角度。無論是在船舶實時路徑的調整還是在初始位置的設定上，都需要憑借環境信息，來確定船舶的位置及避讓的角度。因此，在實時路徑的調整跟初始位置關系上給定如下方程

式中，n為搜尋參數，pik為目前位置參數。

在空間中設定粒子所要產生的數量，接著再通過這一初始位置以及速度去修正路徑移動的位置及速度：

給每顆粒子限制其最大移動速度vmax及最大移動范圍pmax，使粒子的速度跟移動不會超出所設定的范圍，讓控制粒子能在空間范圍中均勻地分布。

式中，ri為權重系數，取值為0 ＜ri＜1。

計算每顆粒子的適應性函數，如下列公式所述

式中，wmax與wmin分別代表w的最大值及最小值。

隨后利用遺傳算法，去調整粒子群中的權重值w。首先決定染色體的范圍以及染色體的總量。計算每條單一染色體的適應性，適應性取決于復制過程或選擇的染色體，進而產生最初親代染色體族群（X1，X2，…，Xn），計算每條染色體的適應性（f（x1）,f（x2）,…,f（xn））。在所有親代染色體中，以適應性的高低為依據，抽選出我們設定比例數量的染色體，再從這些染色體中找出一對適應性最高的染色體進行交配。通過染色體間的交叉運算以及突變，來產生一對子代的染色體。將新的子代染色體加入新的染色體族群。接著重復步驟，直到染色體總數跟初始總數相等為止。以新的子代染色體取代親代染色體，直到滿足終止條件或是目標已經達到優化。

再次檢查粒子的速度限制

同時更新每顆粒子的位置值：

在搜尋范圍中，給每顆粒子一個更新位置值的限制

最后根據粒子最佳位置（PGbest）與最佳適應參數（FGbest）對應的非線性優化目標函數去確定船舶最終避碰路徑的移動方式。

3.3 避碰路徑優化目標函數

在船舶避碰的決策過程中，既要滿足安全性又要滿足經濟性目標，安全性目標主要是通過DCPA來確定，通過設定最小的DCPA 來確定，經濟性通過轉向幅度及避讓里程來確定，具體的優化目標函數為

式中，f1為安全性目標函數值，dDCPA表示距離目標船的最近距離，f2為經濟性目標函數值，P為避碰路徑里程，θ為轉向幅度，α和β分別是權重系數，優化目標函數以最小值為優，這樣得到的避碰路徑安全性及經濟性最好。

3.4 避碰路徑的程序設計

根據以上的PSO-GA 算法模型及優化目標函數，給出本研究的船舶避碰路徑的程序設計流程，如圖2所示。

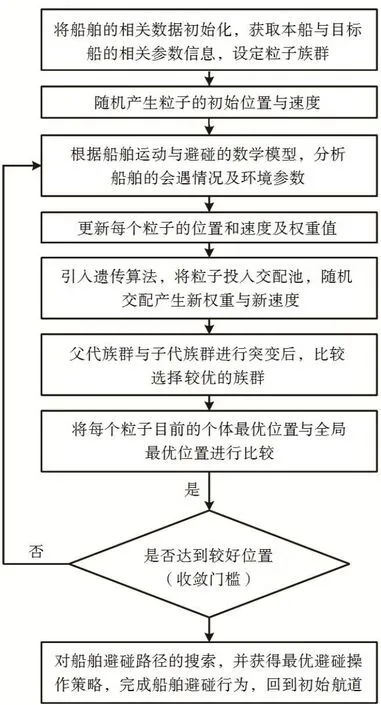
圖2 避碰路徑程序算法流程圖Fig.2 Algorithm flow chart of the collision avoidance path program

4 仿真案例研究

4.1 仿真參數

本研究采用MATLAB 軟件進行仿真分析，仿真平臺采用INTEL 酷睿3.2 GHz 處理器、內存為16 GB的計算機。風向、水密度等環境參數設置為常規參數，本船和目標船的參數如表2所示。結合給定的船舶參數，本研究結合會遇、交叉以及追越三種情況對船舶避碰進行仿真分析，本船為坐標原點，三類情況的目標船信息如表3所示。

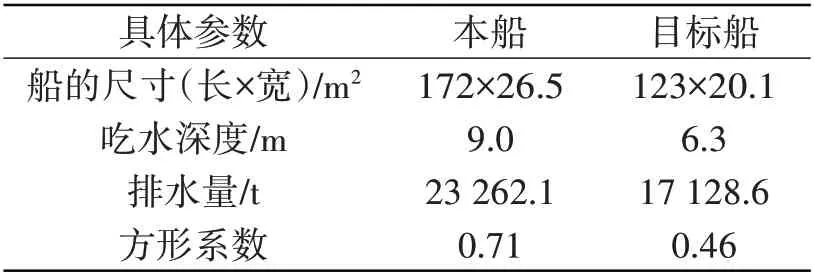
表2 仿真船舶的具體參數Tab.2 Specific parameters of the simulated ship

表3 本船和目標船的不同案例信息Tab.3 Different case information of the standard ship and the sample ship

4.2 仿真結果分析

為了驗證本研究避碰算法的可靠性，對表3給出的三種船舶避碰情況進行分析，參照目標船的方位角分布及距離，給出避碰狀況的初始參數值并輸入算法程序，基于初始化函數視角對路徑進行初期操作。同時使用混合遺傳算法優化船舶避碰路徑。使用遺傳運算符選擇初始群體，使用適度函數確定遺傳過程的質量，獲得全局優化位置，進而完成對船舶避碰路徑的搜索并獲得最優避碰操作路徑求解。圖3 為會遇、交叉和追越三種避碰情況下的船舶避碰路徑軌跡分析以及避碰相距距離分析，圖3（a）～（c）中虛線表示本船和目標船保持原航速航行時的軌跡，實線為本船的實際避碰路徑。圖中用圓形表示本船，方形表示目標船。圖3（d）為三種避碰情況下的相距距離對比分析。

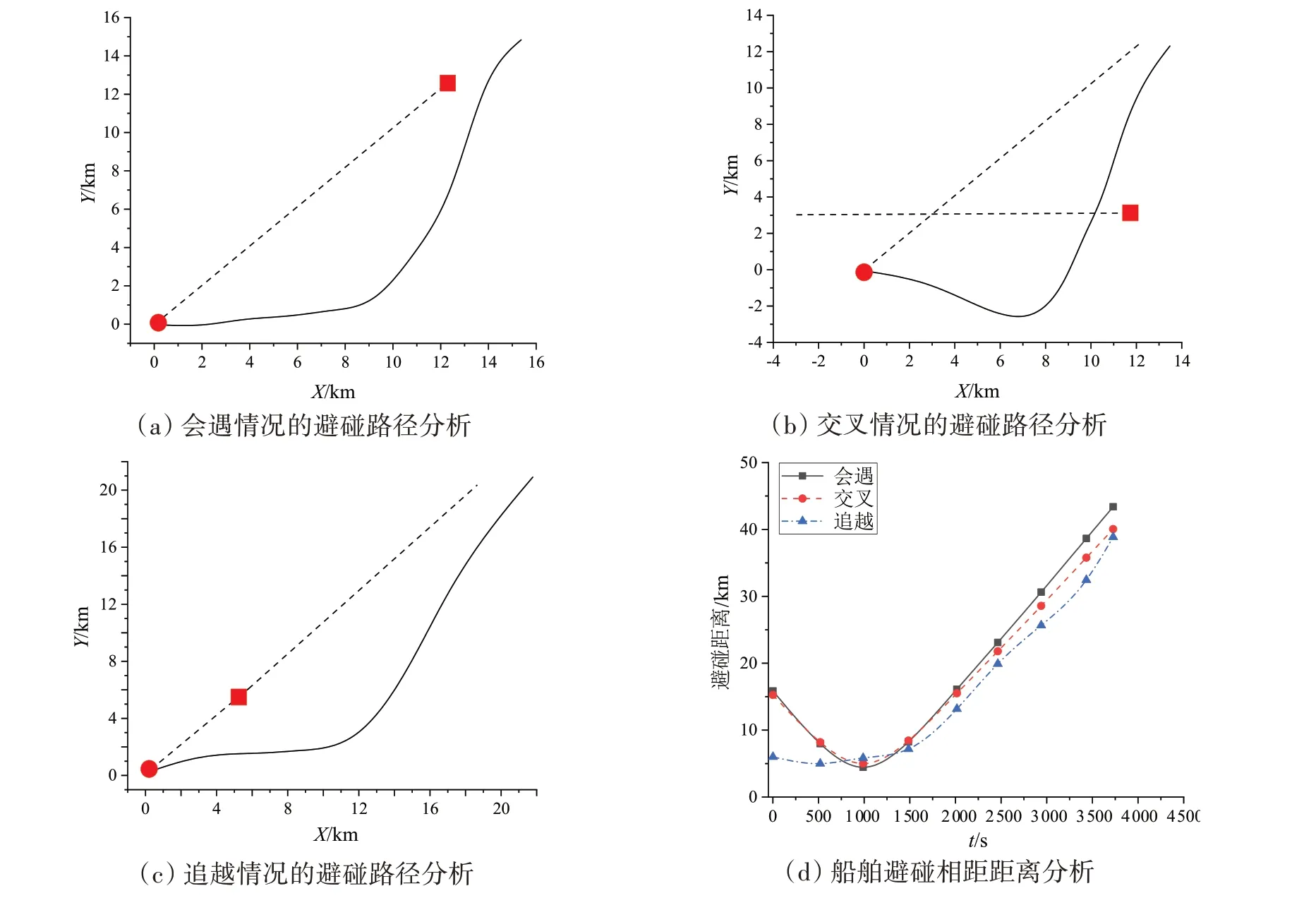
圖3 船舶避碰路徑分析Fig.3 Path analysis of ship collision avoidance

根據圖3 的船舶避碰路徑分析可以看到，在會遇、交叉及追越三種避碰情況下，船舶均能實現安全有效的避讓，且避讓的路徑均為平滑，也即本船與目標船之間的距離均勻變化，滿足了避碰中的安全性要求，同時從圖3（d）的避碰距離可以看到，最小距離均大于5 km，符合了船舶避讓中的寬避讓要求，同時從路徑軌跡中可以看到，三種避碰情況下的目標船最后都接近回到了初始航向軌跡。可見軌跡偏離原航向幅度并不大，滿足了船舶避讓中的經濟性要求。

4.3 算法對比分析

從圖3的分析可以看出，本研究算法的避碰路徑計劃能夠滿足船舶避碰的安全性及經濟性要求，路徑的優化性較好，為了進一步驗證本研究混合遺傳算法的有效性，本研究使用粒子群算法、遺傳算法與本研究算法進行對比，對會遇、交叉及追越三種情況進行仿真模擬，并就仿真模擬的迭代次數和平均最優值進行對比，結果如表4所示。

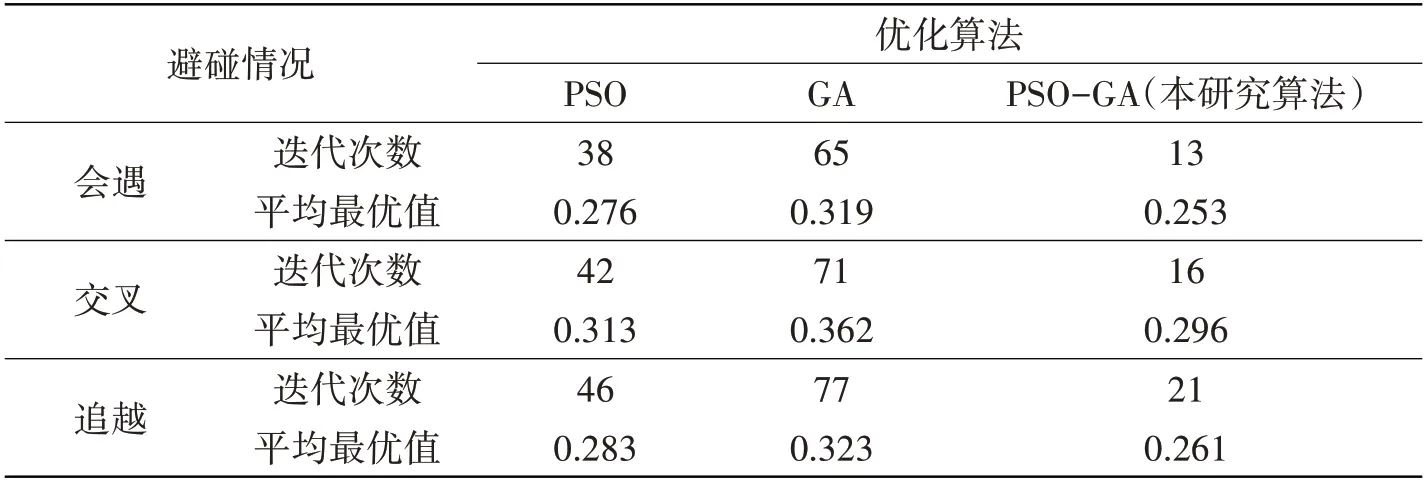
表4 算法的對比分析Tab.4 Comparative analysis of algorithms

根據表4 的對比結果可以看到：在會遇、交叉及追越三種避碰情況下，本研究算法均能在25 次以內完成迭代，其中會遇情況下的迭代次數最少為13 次，這比同樣情況下的粒子群算法及遺傳算法都少了20次以上，算法的收斂速度也得到了較大的提升；同時從平均最優值上也能看到，本研究算法在會遇、交叉及追越三種避碰情況下的平均最優值均小于粒子群算法及遺傳算法，本研究算法的收斂性更好，也即避碰路徑的經濟性及安全性最優。綜上結果，進一步驗證了本研究算法的有效性及高效性。

5 結 語

隨著海上運輸效率的不斷提升，船舶碰撞已經成為影響海上運輸安全的重要因素之一，對于船舶避碰路徑的優化決策分析成為目前研究的熱點。本研究綜合考慮船舶的安全性及經濟性要求，將粒子群算法與遺傳算法進行整合，并應用到船舶避碰路徑的優化分析中，從而構建船舶避碰路徑規劃的優化模型，并結合具體案例，在船舶會遇、交叉及追越三種避碰情況下進行仿真分析。分析結果顯示，本研究給出的粒子群遺傳混合優化算法的收斂速度較快，船舶避碰路徑較為平滑且路徑距離及轉向角度都較小，能夠同時滿足船舶避碰的經濟性及安全性要求，相較單一算法具有顯著的有效性及高效性。