基于SBD技術的小水線面雙體船首尾鰭優化設計

鮑家樂，倪其軍，李勝忠

（中國船舶科學研究中心，江蘇無錫 214082）

0 引 言

首尾鰭作為小水線面雙體船（small water-plane-area twin hull,SWATH）的重要組成部分，具有增加航態穩定性、調整航行姿態以及改善耐波性等作用，是SWATH 設計過程中至關重要的一環。作者參與了一艘6 000 噸級小水線面雙體船的設計任務，該船目前已經完成了主船體的線型優化工作，其阻力性能優越[1]。在使用母船型船變換方法設計首尾鰭時發現，初始方案中首尾鰭需要較大面積和攻角角度才能保證該船在設計航速點航行姿態為尾傾，且總阻力大幅增加約35.8%。因此，需要對該首尾鰭進行優化設計。

首尾鰭的設計最早采用試驗測定和母型船變換的方法，隨后又發展為根據運動穩定性判據保證其縱向運動穩定性，再通過優選方式獲得阻力和姿態能接受的方案。最近幾年，又有多位專家學者通過自動控制理論對首尾鰭進行優化設計。苗飛等[2]通過小水線面雙體船的縱向運動方程和穩定性判別準則，提出了一種首尾鰭設計方法，針對某小水線面雙體船進行了首尾鰭設計工作，并與模型試驗相互驗證，取得較好結果；高占勝等[3]在小水線面雙體船縱向運動穩定性判據的基礎上，分析了首尾鰭的安裝位置、鰭面積等參數變化對該型船不同航速時縱向運動穩定性的影響及規律；Arifah Ali 等[4]在深水中對安裝有首尾鰭的半小水線面雙體船模型進行了靜水阻力試驗，研究了首尾鰭角度對阻力和船體周圍流動的影響。這些方法在工程實踐中發揮了巨大作用，解決了很多工程問題，但在面對本文工程實際問題時，遇到一些困難。比如首尾鰭安裝位置受主船體線型制約，首尾鰭采用成熟產品而導致翼型難有較大變化等問題，很難繼續采用傳統設計方法進行優化。而近年來所出現的基于SBD（simulation based design）技術的構型優化設計方法，能夠在給定約束條件下，以性能最優為目標自動求解優化設計問題，可為本文首尾鰭的優化提供一個新思路。

本文將已用于船型優化設計的SBD 技術[5-6]引入到首尾鰭設計中，建立以性能最優為目標來驅動小水線面雙體船首尾鰭優化設計的方法，并將其應用于目標船首尾鰭的優化設計中。以該船的阻力性能最優為優化目標，選擇首尾鰭面積大小、攻角角度和襟翼形式等參數作為設計變量，在主潛體線型不變的前提下，以小水線面雙體船運動姿態作為約束條件，結合多目標粒子群全局優化算法，綜合集成優化流程，自動優化得出小水線面雙體船首尾鰭的優化設計方案。

1 目標船概況

本文目標船為一艘6 000 噸級小水線面雙體船，其外形如圖1 所示，主要參數見表1，計算模型縮尺比為1:25。根據該船模型試驗結果，在加裝首尾鰭后，該船總阻力大幅增加，主要原因是鰭的升阻比過小，需要較大面積和攻角才能提供足夠升力調整姿態。因此，需要對該首尾鰭進行優化。

圖1 SWATH船示意圖Fig.1 Schematic diagram of SWATH

表1 SWATH船主要尺度參數Tab.1 Principal dimensions of SWATH

2 基于SBD技術的首尾鰭優化設計方法

基于SBD 技術的首尾鰭優化設計方法以優化流程自動化為特點，主要由基于RANS 方程的水動力性能評估技術、首尾鰭幾何變形技術、最優化技術和綜合集成技術等組成。

2.1 基于RANS方程的水動力性能評估技術

水動力性能評估技術是整個優化技術的基礎，其預報精度是確保設計優化結果的關鍵因素。本文采用基于RANS 方程的高精度粘流數值評估軟件，結合重疊網格技術，對目標船阻力性能和運動姿態進行預報，其可靠性在多個船型設計中已經得到了應用與驗證，具體評估流程可參見文獻[7-8]。

本文首先對該船進行水動力性能預報，將裸船體、首尾鰭、舵以及背景流域進行單獨劃分，然后生成計算網格，如圖2所示。再將各個部分進行合并，構成一個完整的小水線面雙體船全附體重疊計算域。然后采用二因次傅汝德法換算到實船后與模型試驗結果進行對比驗證，如表2所示。

圖2 重疊計算網格Fig.2 Overlap grid of SWATH

表2 數值計算與模型試驗結果對比Tab.2 Numerical and experimental results of SWATH

對比結果表明，通過數值計算得到的總阻力誤差基本在3%以內，升沉值和縱傾角趨勢與模型試驗結果基本一致，驗證了本文所采用的水動力性能評估技術是可靠的。

2.2 最優化技術

最優化技術也是首尾鰭優化設計技術中的關鍵之一，是指導優化設計方向的主要技術手段。本文最優化技術采用多目標粒子群全局優化算法，該算法已在船型優化設計中得到了應用[5-6]。

2.3 首尾鰭參數化表達與變形技術

首尾鰭參數化表達與變形技術是SBD 優化技術的前提條件。本文選擇基于CAD 的變形方法和自由變形方法（free-form deformation approach,FFD）作為幾何變形重構方法[8]，并采用計算網格自適應技術[9]，使首尾鰭計算網格能夠隨鰭外形變化而自適應變化。

2.4 綜合集成技術

保證首尾鰭優化設計流程能夠自動進行的關鍵技術就是綜合集成技術，它也是將優化設計方法中各個模塊串聯起來的主干。本文采用C++語言將以上各個模塊的輸入與輸出進行連接交互，按照優化流程進行迭代整合，最終建立起一個完整有序的優化設計平臺。

3 首尾鰭優化設計

本文采用基于SBD技術的首尾鰭優化設計方法，針對6 000噸級小水線面雙體船首尾鰭進行優化設計，解決該船在加裝首尾鰭后在經濟航速點模型總阻力增加35.8%，以及在設計航速點出現埋首現象的問題。

3.1 優化對象

本文的優化對象為6 000 噸級小水線面雙體船首尾鰭，其外形如圖3 所示。首尾鰭的面積大小、安裝位置、角度均采用上文中模型試驗結果。

圖3 SWATH船首尾鰭示意圖Fig.3 Schematic diagram of stabilizing fins of SWATH

3.2 目標函數

本文針對小水線面雙體船阻力性能進行優化，選擇在小水線面雙體船的經濟航速（11 kn）與設計航速（15 kn）點對首尾鰭進行優化設計。將這兩個點的阻力值作為目標函數，如下式所示：

式中，F1、F2為構建的目標函數，Rt1為小水線面雙體船在11 kn 時的總阻力，Rt2為其在15 kn 時的總阻力，Rt10為初始方案11 kn時的總阻力，Rt20為初始方案15 kn時的總阻力。

3.3 設計變量

參考首尾鰭相關文獻以及本船工程實際情況，本文選擇首尾鰭面積和攻角作為設計變量，再通過增加襟翼和改變后掠角進一步提高升阻比（首尾鰭襟翼形式如圖4所示，襟翼變化如圖5所示）。考慮到尾鰭襟翼會影響槳盤面處的伴流，進而影響推進效率，故襟翼僅選定在首鰭處進行添加。

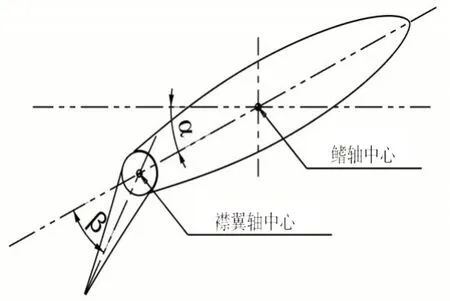
圖4 首尾鰭襟翼形式Fig.4 Diagram of wing flap of fins

圖5 首尾鰭襟翼變化Fig.5 Variation of angles of wing flap of fins

因此，文中首尾鰭的設計變量選擇為首鰭的面積S1、首鰭主翼的攻角角度α1、首鰭襟翼的攻角角度β、首鰭的前緣后掠角γ1、尾鰭的面積S2、尾鰭的攻角角度α2和尾鰭的前緣后掠角γ2。

3.4 參數化表達變形

基于SBD技術的首尾鰭優化設計方法的核心在于如何實現首尾鰭自動變形重構。

本文首先采用FFD 自由變形方法，將首尾鰭置入控制體框架內。將控制體外側剖面內所有的控制頂點沿著首尾鰭長度方向進行平移，然后通過逐層線性插值的方式，將控制體最外側控制頂點變化向內側傳遞，實現后掠角變化，如圖6 所示。將襟翼與主翼進行分割（尾弦比為0.25），采用基于CAD直接方法將襟翼部分的所有控制頂點坐標繞襟翼軸中心進行旋轉，再將襟翼前端與主鰭末端進行連接修飾，完成首尾鰭襟翼變化。通過網格生成軟件Gridgen 宏文件（fin_modify.glf）直接將首尾鰭表面控制頂點進行縮放和旋轉，即能實現首尾鰭面積和主翼攻角的調整，如圖7所示。

圖6 首尾鰭后掠角變化Fig.6 Sweepback variation of fins

圖7 首尾鰭面積與主翼攻角變化Fig.7 Variation of areas and attack angles of fins

在首尾鰭的形狀發生變化后，采用計算網格自適應技術將計算網格與首尾鰭的幾何外形結合起來，直接對鰭表面網格（首尾鰭幾何外形）進行自動變形重構，使得整個計算網格能夠跟隨首尾鰭表面網格發生變化的同時一起自適應變化。這樣既能保證計算網格的質量，也能提高其適應性。

在完成首尾鰭的體網格變形后，結合重疊網格技術將船體各個部分體網格和背景網格重疊，形成最終完整的計算域。

3.5 約束條件

根據升力公式重新估算首尾鰭面積并參考相關文獻[10-12]確定設計變量變化的上下限，以及設計任務需求中對主船體航行姿態的約束，約束條件如表3所示。

表3 約束條件Tab.3 Constraint of optimization

3.6 優化過程

首先將模型試驗結果作為初始方案，采用粒子群全局最優算法對設計變量進行調整，通過FFD自由變形方法實現首尾鰭后掠角發生變化，再通過基于CAD的變形方法實現首尾鰭襟翼轉動、面積縮放和攻角旋轉；在完成面網格修改后，通過計算網格自適應技術獲得修改后的首尾鰭計算網格文件；采用重疊網格技術合并成計算域后對小水線面雙體船的水動力性能進行計算，獲得目標函數值；然后通過目標函數值判斷該結果是否滿足約束條件，若滿足則作為一組可行解，若不滿足則需要將其去除；最后判斷是否滿足迭代停止條件，若滿足則結束迭代，若不滿足則繼續采用粒子群算法獲取新的設計變量值，開始下一輪的迭代。

4 首尾鰭優化結果及分析

本文所采用的多目標粒子群優化算法種群粒子數為40，經過9 輪迭代后，目標函數F1、F2趨于收斂，可行解解集如圖8 所示。圖中“”表示最優解，其連線構成Pareto前沿。

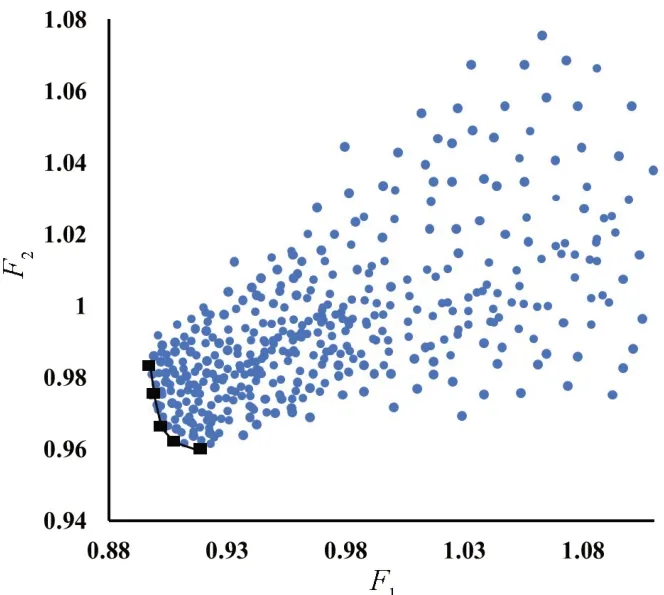
圖8 目標函數解集Fig.8 Schematic diagram of target solution set

本文在最優解集中選擇了5 個最優解，所對應的目標函數值、設計變量如表4 所示。

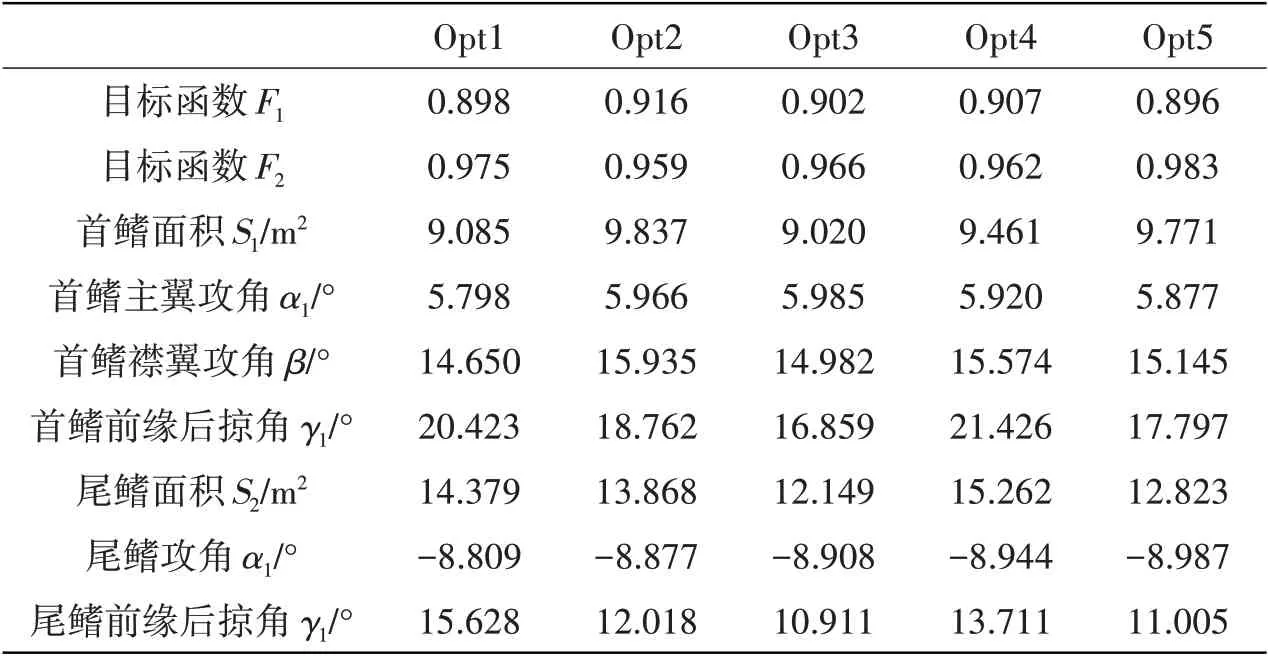
表4 首尾鰭優化結果Tab.4 Optimization result of stabilizing fins of SWATH

兼顧目標函數F1和目標函數F2，本文最終選擇優化可行解Opt3 作為最終優化方案。最終得到的首尾鰭方案如表5 所示。初始方案與優化方案首尾鰭外形對比如圖9所示。

圖9 初始方案與優化方案首尾鰭外形對比Fig.9 Comparison of appearances between the optimized plan and original one

表5 初始方案與優化方案首尾鰭參數對比Tab.5 Comparison of parameters of stabilizing fins between the optimized plan and the original one

在優化過程中，為了快速分析優化效果，只在經濟航速點與設計航速點進行了阻力性能預報。現對優化方案進行全航速總阻力以及運動狀態預報，并與初始方案進行對比，結果如表6所示。

表6 初始方案與優化方案數值預報結果對比Tab.6 Comparison of numerical prediction with the optimized and original plans

通過對比分析可以發現，優化方案在整個航速段中均有減阻收益，在經濟航速附近區域（8～11 kn）優化效果較為明顯，經濟航速點總阻力減少了9.8%，在設計航速區域附近總阻力減幅較小，設計航速點總阻力減少3.4%。

在總阻力減小的同時，小水線面雙體船的運動情況也優于初始方案，經濟航速點升沉值由-1.502 mm減少為-0.951 mm，縱傾角增加了0.087°；設計航速點升沉值由-6.163 mm 減少為-4.514 mm，縱傾角由-0.068°增加為0.061°。在設計航速點該船的運動姿態已經由首傾狀態調整為尾傾狀態。

5 結 語

本文將用于船型優化設計的SBD 技術引入首尾鰭優化設計過程中，建立了以性能最優為目標來驅動小水線面雙體船首尾鰭優化設計的方法。選取首尾鰭的面積、主翼攻角、襟翼攻角、后掠角等參數為設計變量，在主潛體型線不變的情況下，以經濟航速與設計航速總阻力為目標函數，以小水線面雙體船運動姿態作為約束條件，采用多目標粒子群優化算法，對6 000 噸級小水線面雙體船首尾鰭優化設計問題進行了求解，最終獲得了阻力性能與航行姿態較優的設計方案。優化方案總阻力在整個航速范圍內均有減小，在經濟航速區域收益尤為明顯，總阻力減少了約10%。此外，優化使初始方案設計航速點從處于首傾狀態轉為尾傾狀態。