運用微課拓展初中數(shù)學教材的探索

謝春平

【摘要】目前，初中數(shù)學教材存在著一定的局限性，教師在教學中必須對其內(nèi)容進行有效補充.初中數(shù)學教材的拓展成效在實際教學中沒有得到很好的體現(xiàn).本文將針對如何利用微課進行初中數(shù)學教材拓展進行深入研究.

【關鍵詞】微課教材;拓展;個性化教學

一、正視教材拓展存在的問題

1.不能適應學生“實際”

教師在對教材進行拓展及編寫時，容易忽視學生的實際情況，導致拓展的教材內(nèi)容與學生的接受能力脫節(jié).此種拓展方式雖然使教材具有深度，但教師缺乏對尺度的把握，忽視了學生是否能夠完全理解拓展內(nèi)容.

2.不能滿足教學“實需”

教材的拓展應以課標為核心，從教材出發(fā)，以滿足教學需求為目標.但在現(xiàn)實中，很多教師無法確定教學的實際需求，而對教材進行盲目拓展，使教材拓展工作流于表面，根本無法滿足教學的實際需要.

3.不能體現(xiàn)學科“實質(zhì)”

教材的拓展應是為教學活動服務的，目前很多教師在進行教材拓展時，會加入很多低效和無效的內(nèi)容，反而增加了學生理解數(shù)學概念的困難.若教材的拓展不能進一步體現(xiàn)學科的實質(zhì)，則會導致教材拓展工作徒勞無功.

二、對微課運用方式的建議

當前人們對微課運用的認識更多集中在如何使其主要載體——視頻，變得更加豐富.一種現(xiàn)代教育技術與另外一種現(xiàn)代教育技術相結合的方式是人們普遍能夠接受的方式，比如幾何畫板+微課、Flash動畫+微課等.總之，大多數(shù)課堂教學中信息技術都可以與微課結合在一起，這樣，微課的離線教學功能就被無限放大.與課堂面授教學相比，微課的主要優(yōu)勢就是打破時間與空間的局限.但如果過分依賴某種單一形式的教育模式，那么即使它具有鮮明的特點和強大的功能，也很容易使整個教學體系變得索然無味.相比于傳統(tǒng)意義和方式下的微課教學，將微課與課堂教學相融合會給微課教學本身帶來更多機動性，而此時的微課視頻在整個教學過程中更多起到輔助作用.

如果把微課與課堂教學結合在一起，那么就會發(fā)現(xiàn)，微課原本的功能沒有發(fā)生任何變化，只是由于它在教學中扮演的角色變了，其作用和在學習中的地位自然發(fā)生了改變.需要指出的是，這種應用模式下的微課內(nèi)容更多的是一些與課堂教學相關的零散碎片，比如重點和難點的應用案例、學習資料拓展、舊知識與新知識的銜接案例等，這樣更有助于學生消化和吸收教師所講的知識點.對于具體應用案例，筆者將會在后面做詳細闡述.

三、運用微課拓展教材的策略

1.抽象概念拓展形象化

在初中數(shù)學中，數(shù)學概念是一切數(shù)學學習的開端，也是解題的基礎.但是，數(shù)學概念具有枯燥、抽象的特點，在很多人心中是冰冷、死板的代名詞.這也是導致很多學生對數(shù)學概念學習缺乏興致的原因.

因此，教師應通過拓展教材改變學生對數(shù)學概念的刻板印象.此時，教師可巧妙地應用微課，對數(shù)學概念進行形象化拓展，使數(shù)學概念的教學更加生動且富有趣味性.通過微課激發(fā)學生的多種感官刺激，培養(yǎng)學生的數(shù)學思維，提高學生的學習興趣.

2.復雜關系拓展圖示化

數(shù)學知識點不是完全獨立存在的，不同的知識點之間存在著千絲萬縷的聯(lián)系.而學生尚未熟練掌握所有數(shù)學知識，因此很難自主發(fā)現(xiàn)知識點間的關聯(lián).教師可通過微課將數(shù)學知識的復雜關系直接呈現(xiàn)出來.在教學中，教師可以精準抓住新舊知識點間的聯(lián)系，利用微課設計出一系列導向性問題，并將問題進行連接，最后將數(shù)學關系形成具體的圖像，幫助學生構建出有效的數(shù)學認知框架.

3.靜態(tài)知識拓展動態(tài)化

教材具有簡單、明了的特點，但因為教材屬于靜態(tài)的工具，所以學生在將靜態(tài)的知識轉化為動態(tài)的過程時，會存在一定的困難.而微課能夠?qū)滩闹徐o態(tài)的知識進行動態(tài)化拓展.教師可以將靜態(tài)的知識通過微課轉化為動態(tài)化的信息，以提高學生的思維靈活度，加深學生對數(shù)學知識的理解.利用微課進行靜態(tài)知識拓展時，教師需要熟練掌握微課設計的方法，同時充分挖掘教材內(nèi)容中的“動”的因素，進行合理設計，使微課起到輔助作用.對于最基礎的平移、旋轉等圖形變化，微課的設計相對簡單，教師可直接利用微課呈現(xiàn).對于函數(shù)概念、數(shù)據(jù)統(tǒng)計等不具備明顯動態(tài)特征的數(shù)學知識，教師可通過微課將信息進行動態(tài)呈現(xiàn)，從而加深學生對相關知識的印象及理解.

四、運用微課進行教材拓展的實例分析

下面以“圖形的位似”這一課題為例，敘述微課在教材拓展中的多種應用方法.

1.利用微課設疑，突出教學重點

在初中數(shù)學課堂中，教師可以利用微課創(chuàng)設具體情境，使學生在思考、猜測與解題過程中探索數(shù)學知識.

首先，觀看微課.教師可以先在微課中，畫出兩個相似的多邊形，然后對微課中的內(nèi)容進行提問.學生觀察兩個多邊形的相似性，然后用刻度尺及量角器對兩個圖形進行自主測量.教師可鼓勵學生說出自己的發(fā)現(xiàn).

其次，教師對學生的發(fā)現(xiàn)進行歸納，總結出位似形的定義.教師根據(jù)定義進行提問：

（1）位似形的圖形皆為（ ）;

（2）所有通過對應頂點的直線都經(jīng)過（ ）;

（3）對應邊相互（ ），或在同一直線;

（4）（ ）是各對應頂點與位似中心的距離比.

2.運用微課對教材進行靈活拓展

教材對位似的相關概念呈現(xiàn)得十分精準，但相關教學內(nèi)容較少，因此教師需要通過微課對教材內(nèi)容進行拓展.教師可在微課中提供相應的典型例題，使教材實現(xiàn)深度與廣度的拓展，同時使學生加深對相關知識的理解.

例題：（1）為學生提供任意一個三角形，利用位似圖的概念，將原圖的邊縮小為原來的1/3.

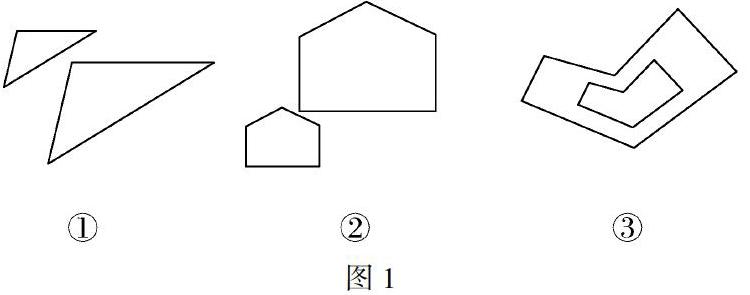
（2）觀察以下位似圖（見圖1），找到它們的位似中心.

3.利用微課對相關知識進行串聯(lián)，實現(xiàn)教材拓展

微課可以將常規(guī)練習題轉換為閱讀題，同時體現(xiàn)問題的層次性，幫助學生在解題中將新舊知識進行串聯(lián)，使學生自主對課堂知識進行拓展，在理解課內(nèi)知識的同時，自主獲取課外知識.

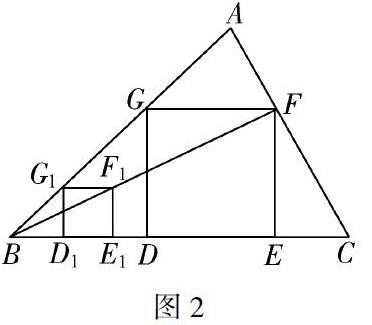
例題：已知銳角三角形ABC如圖2.求作：正方形DEFG，使D，E落在BC的邊上，F(xiàn)、G分別落在AC、AB的邊上.

教師可以將作圖的過程通過動態(tài)的微課呈現(xiàn)出來，最后將作圖方法概括成文字，并對學生進行提問.

問題：（1）為何四邊形DEFG為正方形？

（2）上述作圖應用的是什么作圖方法？

（3）設△ABC中，BC=120，BC邊上的高為80.計算正方形DEFG的邊長.

（4）若把（3）中的正方形DEFG改為矩形DEFG，且DG=2GF，其他條件不變，此時GF的長是多少？

4.利用微課培養(yǎng)學生的創(chuàng)新性

若想培養(yǎng)學生的創(chuàng)新思維，教師不僅要在課堂中激發(fā)學生的創(chuàng)新意識，還要通過微課對課堂內(nèi)容進行總結，對教材內(nèi)容進行補充.教師可在微課中將碎片化的知識點以“提問—回答”的方式傳播給學生，使學生在頭腦中建立知識框架.在思考中，學生能夠?qū)崿F(xiàn)思維的創(chuàng)新.

例題：（1）位似圖形的概念是什么？它具有什么性質(zhì)？它為何可以將圖形進行放大和縮小？如何確定位似中心？

（2）位似畫圖的步驟是什么？畫圖過程中，位似中心的的作用是什么？

五、運用微課進行教材拓展的深入思考

如何對教學內(nèi)容進行進一步拓展一直都是教師們比較重視的問題，因為對教學內(nèi)容進行拓展能強化學生的邏輯思維，培養(yǎng)并發(fā)展學生的發(fā)散思維.長期以來，大多數(shù)教師在指導和引導學生自主探索的過程中都格外注意培養(yǎng)他們的自主學習能力.記得在教學三角函數(shù)時，筆者通常會將總結好的公式、定理直接灌輸給學生，并要求他們直接將公式、定理應用于做題中.很難說這種做法是錯誤的，但在培養(yǎng)學生學習能力上，這種做法是有待商榷的.

隨著微課在初中教學的普及，筆者嘗試在課前錄制一些與課堂教學有關的視頻，并將這些視頻分門別類地壓縮成“溫故包”“提醒包”“進階包”，每個“包”里有2～3個視頻.“溫故包”里裝有與當堂課有關的視頻內(nèi)容;“提醒包”里裝有當堂課的教學重點、難點;“進階包”里裝有延伸拓展知識.每個視頻都包含一些應用案例或公式推導過程、定理證明過程等.學生在上課前可以觀看“溫故包”里的視頻，以便更好地與當堂課所學的內(nèi)容建立起聯(lián)系.由于課堂教學時間有限，教師不可能對每一個問題都進行細致的講解.所以對于案例講解和公式推導，筆者主張學生觀看“提醒包”里的視頻.

比如在教學直角三角形的三角函數(shù)時，筆者會結合角的正弦、余弦表達式及角的正切、余切表達式，直接給出正余弦關系式和正余切關系式.推導過程的講解筆者會放在視頻里，感興趣的學生可以直接在課上進行觀看.如果時間允許，筆者會組織學生集體觀看.在接下來的教學中，對于任意銳角的正弦、余弦、正切、余切，筆者會以同樣的方法展開教學.這時，“溫故包”的功能便會發(fā)揮出來，有疑惑的學生就可以參照前面的內(nèi)容進行學習.

在教學稍難一點的公式時，如兩角和與差的公式、倍角公式、三倍角公式、半角公式、萬能公式、積化和差公式、和差化積公式等，筆者會將推導過程與案例應用分別錄制成兩組不同的視頻.因為按照教學要求，學生不需要完全掌握整個推導過程，能夠應用解決即可，但從自主學習和自主探究能力的培養(yǎng)上看，應用基本公式推導出復雜公式的過程，是不可缺少的學習環(huán)節(jié).

之所以會將推導過程和案例應用以微課的形式呈現(xiàn)出來，主要是因為視頻本身具有很好的指導作用，能給予學生更好的點撥，這也是設計“進階包”的主要意圖.對于那些有興趣了解推導過程的學生來說，“進階包”里面的內(nèi)容進一步充實和豐富了他們的數(shù)學知識.

微課的運用方式是多樣化的，重點在于我們?nèi)绾螌⑺c課堂教學有效銜接在一起，以滿足每名學生的學習需求.

總 結

伴隨著微課技術的不斷成熟，它在初中數(shù)學教材拓展中的作用愈加明顯.初中教師應熟練掌握對微課的應用，從而實現(xiàn)對教材的有效拓展.

【參考文獻】

[1]胡美玲.基于微課的初中數(shù)學智慧課堂構建及案例研究[J].才智，2019（27）：51.