基于傅里葉級數(shù)擬合實現(xiàn)的三電平SHEPWM

李穎川，王琛琛，董志強

（北京交通大學(xué)電氣工程學(xué)院，北京 100044）

隨著現(xiàn)代工業(yè)的快速發(fā)展，三電平中點箝位NPC（neutral point clamped）型逆變器作為多電平逆變器之一，憑借其輸出諧波含量低和開關(guān)器件承受的電壓應(yīng)力小等優(yōu)勢，在中高壓和大功率場合中廣泛應(yīng)用[1-2]。

在大功率場合，為降低逆變器的損耗，需降低開關(guān)器件的開關(guān)頻率，但在低開關(guān)頻率下，常規(guī)的載波調(diào)制和空間矢量調(diào)制已經(jīng)無法適用[3]。為滿足系統(tǒng)在低開關(guān)頻率下的運行要求，研究學(xué)者提出特定諧波消除脈寬調(diào)制SHEPWM（specific harmonic elimination pulse width modulation）法和電流諧波最小脈寬調(diào)制CHM-PWM（current harmonic minimum pulse width modulation）法[4]等優(yōu)化PWM 法，其中SHEPWM 應(yīng)用最為廣泛。

SHEPWM 目前常用的實現(xiàn)方式有在線實現(xiàn)和離線計算，其中離線計算分為查表法和曲線擬合法。但兩電平SHEPWM 與三電平SHEPWM 相比，其開關(guān)角軌跡的線性程度更高，采用多項式曲線擬合法較為簡便，而三電平SHEPWM 的開關(guān)角軌跡變化較大，查表法與多項式曲線擬合法都存在缺點。如文獻[5]采用兩種方法實現(xiàn)三電平SHEPWM 的在線計算，其中：第一種為查表法與線性插值法相結(jié)合，減少查表數(shù)量，但表格數(shù)據(jù)的數(shù)量較多；第二種是將開關(guān)角軌跡擬合得開關(guān)角度，使用所得開關(guān)角度作為牛頓迭代的初值，利用牛頓迭代法在線求解開關(guān)角度，但會出現(xiàn)迭代不收斂的情況。文獻[6]采用多項式曲線擬合法實現(xiàn)三電平SHEPWM，但在高調(diào)制比區(qū)域，需多段擬合才能達到擬合精度的要求。由此，研究學(xué)者提出了其他實現(xiàn)三電平SHEPWM 的方式。如文獻[7]采用基于遺傳算法的在線計算開關(guān)角的方法，計算過程中無需給定初值和預(yù)測解的變化趨勢，易收斂且計算時間縮短，但實現(xiàn)過程較為復(fù)雜；文獻[8]采用基于遺傳算法優(yōu)化的BP（back propagation）神經(jīng)網(wǎng)絡(luò)實現(xiàn)在線計算，計算時間短，且無需給定初值，但實現(xiàn)較為麻煩。

與多項式曲線擬合法類似，傅里葉級數(shù)擬合法可用于擬合曲線，多用于鐵路客運量、自然災(zāi)害損失、電力系統(tǒng)日負荷量、數(shù)據(jù)信號和抽樣調(diào)查數(shù)據(jù)等周期性曲線處理[9-10]。此外，傅里葉級數(shù)擬合也可用于非周期性曲線的擬合[11]，如凸輪升程曲線[12]。

本文以三電平NPC 為研究對象，采用傅里葉級數(shù)擬合法實現(xiàn)三電平SHEPWM 開關(guān)角軌跡曲線的擬合，并與常用的多項式曲線擬合法對比。最后，通過仿真及實驗驗證了傅里葉級數(shù)擬合法的可行性。

1 SHEPWM 基本原理

圖1 為三電平NPC 逆變器三相拓撲，圖2 為三電平NPC 逆變器的輸出相電壓波形。

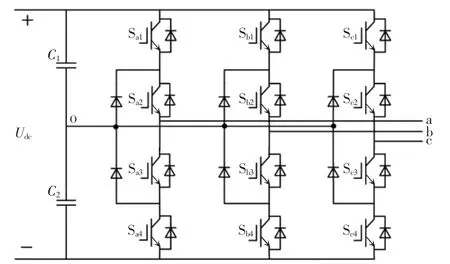
圖1 三電平NPC 逆變器拓撲Fig.1 Topology of three-level NPC inverter

SHEPWM 將三電平逆變器輸出的相電壓波形通過傅里葉級數(shù)展開，為消除特定次諧波而得到一組非線性方程組。通過求解非線性方程組，可得各個開關(guān)角度。

圖2 中，a 相電壓Ua的輸出波形由傅里葉級數(shù)展開為

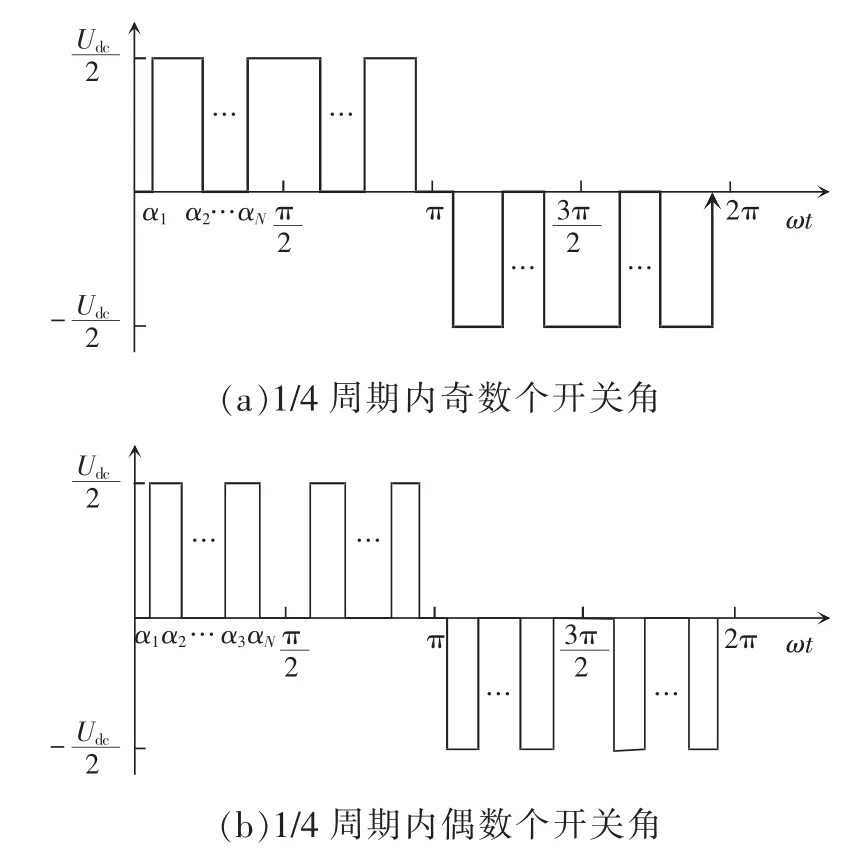
圖2 三電平NPC 逆變器輸出相電壓波形Fig.2 Waveforms of output voltage of three-level NPC inverter

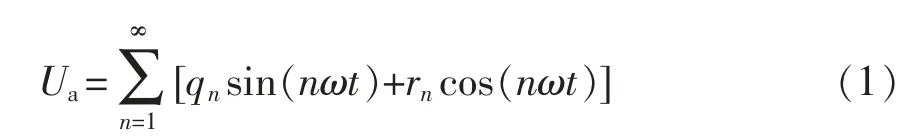
式中：n 為基波和各次諧波次數(shù)；ω 為角頻率；t 為時間；qn和rn分別為相電壓波形中正弦分量和余弦分量的幅值，分別表示為

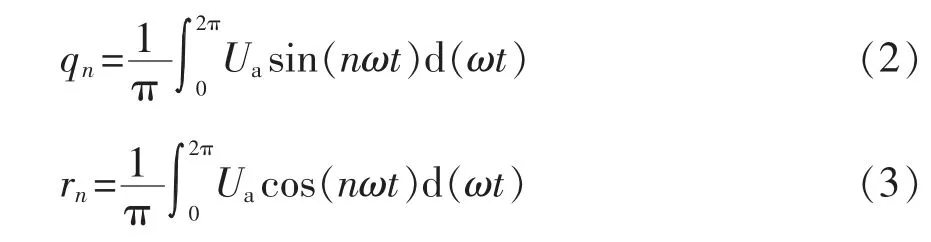
圖2 中：α1，α2，…，αN為開關(guān)角；N 表示開關(guān)角個數(shù)；Udc為直流側(cè)總電壓。輸出相電壓波形具有半波對稱和1/4 周期對稱的特點，因此輸出波形所含的諧波成分中不存在偶次分量，可得

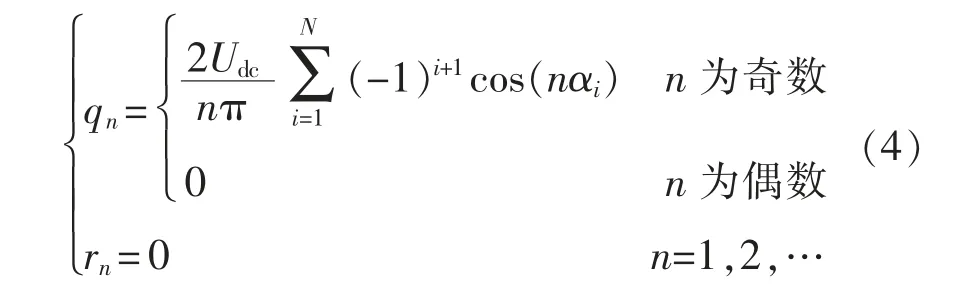
當(dāng)輸出側(cè)接三相對稱負載時，3 的倍數(shù)次諧波在線電壓中相互抵消，只需考慮消除6k±1（k=1，2，…）次諧波，可得基波（即n=1）分量和n 次（n=6k±1，k=1，2，…）諧波分量的電壓幅值分別為

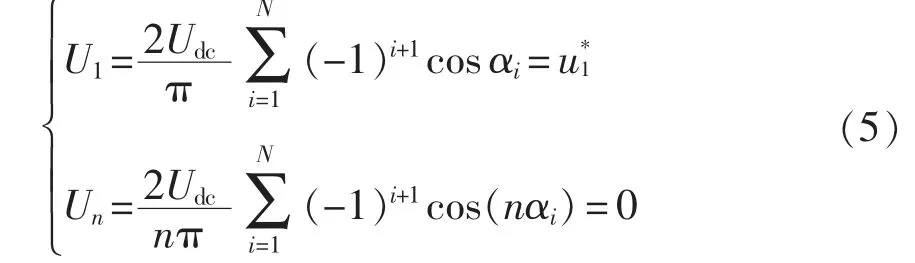
取直流側(cè)總電壓Udc的一半即Udc/2 為基值進行標(biāo)幺化，則式（5）可變?yōu)?/p>

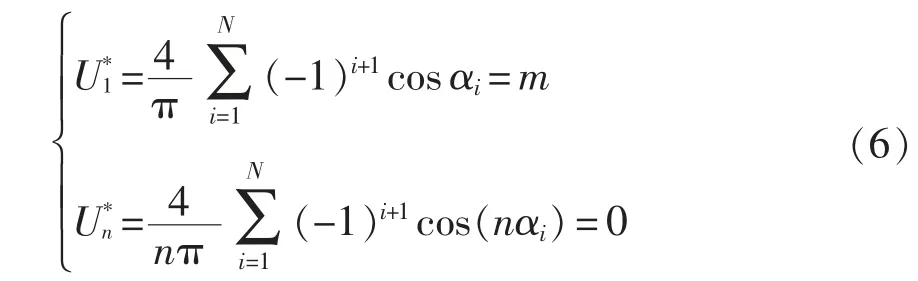
式（6）中，N 個開關(guān)角構(gòu)成含有N 個方程的非線性方程組，消除N-1 個特定次諧波，如N=7 時，消除5、7、11、13、17 和19 次諧波。

求解式（6）的非線性超越方程組，目前有遺傳算法[7]、牛頓迭代法[13]、同倫迭代算法[14]、蟻群算法[15]等方法，本文采用牛頓迭代法進行求解。牛頓迭代法求解的關(guān)鍵是迭代初值的選取，因為迭代初值與解的收斂性有關(guān)。本文采用文獻[13]中迭代初值的選取方法，得到開關(guān)角隨調(diào)制比m 變化的軌跡曲線，如圖3 所示。由圖3 可知，在低調(diào)制比區(qū)，開關(guān)角與m 接近線性關(guān)系；在高調(diào)制比區(qū)，開關(guān)角軌跡變化較大。

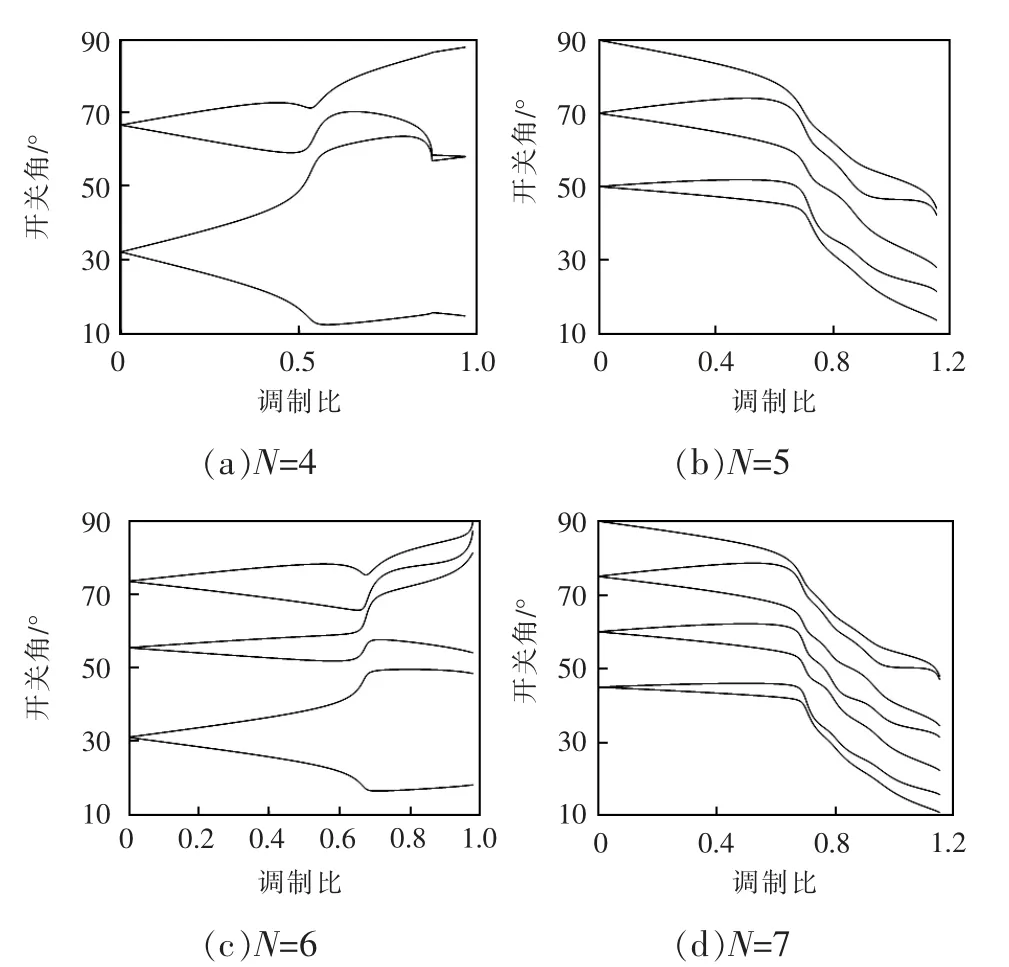
圖3 不同開關(guān)角個數(shù)下開關(guān)角度隨調(diào)制比的分布Fig.3 Distribution of switching angle with variable modulation ratio under different numbers of switching angle

2 曲線擬合法

2.1 多項式曲線擬合法

多項式曲線擬合法廣泛應(yīng)用于曲線擬合。在開關(guān)角軌跡曲線擬合中，第i 個開關(guān)角αi的曲線擬合表達式為

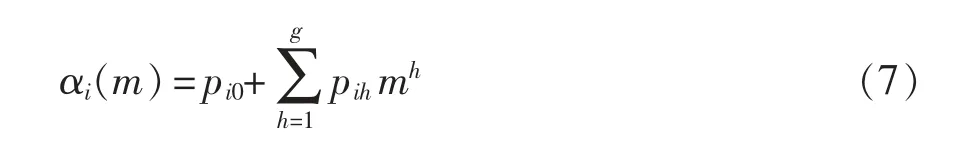
式中：i=1，2，…，N；m 為調(diào)制比；pi0，pi1，…，pih為多項式擬合系數(shù)；h 為pih對應(yīng)的擬合階數(shù)，且h=1，2，…，g；g 為所選擬合階數(shù)，g 越大，擬合曲線越逼近原曲線，擬合誤差越小。當(dāng)擬合曲線的波動過大時，即便g 增大，擬合誤差依舊很大，則需采用分段擬合，以減小擬合誤差。

鑒于多項式曲線擬合法在不分段的情況下，擬合曲線波動過大時擬合誤差過大。為減小擬合誤差需多次試驗尋找分段點進行分段的缺點，本文提出采用傅里葉級數(shù)擬合法來擬合開關(guān)角曲線。

2.2 傅里葉級數(shù)擬合法

對于周期性曲線，傅里葉級數(shù)展開式為

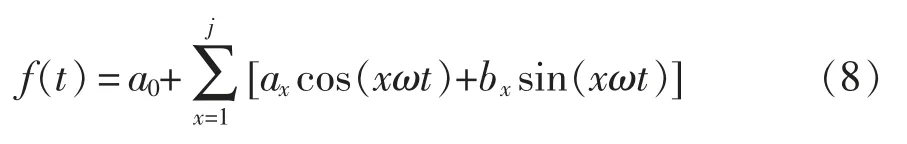
式中：a0，a1，a2，…，aj和b1，b2，…，bj為傅里葉系數(shù)；x為ax和bx對應(yīng)的擬合階數(shù)，x=1，2，…，j；j 為選定的展開階數(shù)。若j 選取過大，會增大計算量；若j 選取過小，則無法滿足擬合精度的要求，所以需要選取適當(dāng)?shù)膉 值。

采用傅里葉級數(shù)擬合法擬合開關(guān)角軌跡曲線時，傅里葉級數(shù)展開式為

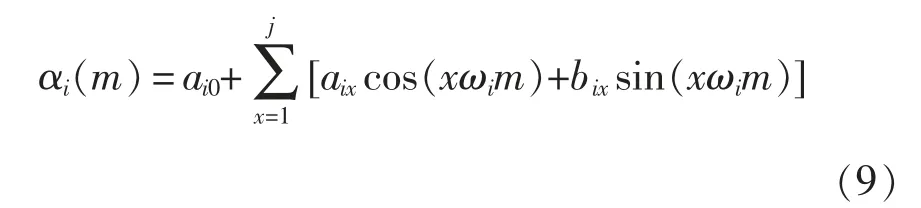
式中：i=1，2，…，N；ωi為開關(guān)角αi曲線擬合時對應(yīng)的角頻率。

由于開關(guān)角軌跡曲線為非周期性曲線，可將其看作某個周期性曲線的某一部分進行傅里葉級數(shù)展開。在非周期性曲線中，ωi和傅里葉系數(shù)由非線性最小二乘法[16]計算得出。

計算ωi，ai0，ai1，ai2，…，aij，bi1，bi2，…，bij的具體實現(xiàn)過程如下。

定義向量

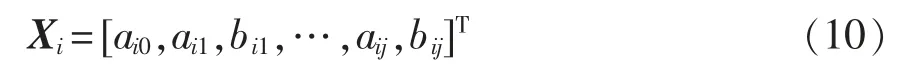
根據(jù)式（9），在全調(diào)制比范圍內(nèi)，將m 等份劃分為λ 份，則λ 份mλ滿足

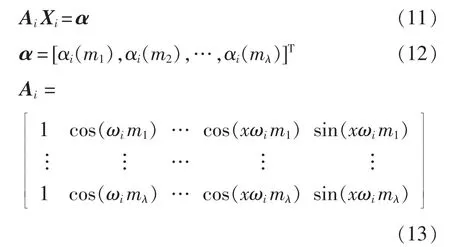
當(dāng)滿足j≤λ/2 時，通過非線性最小二乘法計算Xi和ωi；若不滿足j≤λ/2，則求解的未知數(shù)多于方程個數(shù)，無法求解Xi和ωi。

以N=7 的開關(guān)角軌跡為例，分別采用多項式曲線擬合法和傅里葉級數(shù)擬合法進行曲線擬合，在擬合精度為±1.5°下對比分析。曲線擬合情況如圖4～圖6 所示，其中圖4（a）、圖5（a）和圖6（a）中實線為原軌跡曲線，虛線為擬合軌跡曲線。圖4（a）和圖5（a）中的第1 分段和第2 分段以及圖5（a）中的第3分段表示分段擬合區(qū)域。

圖4 為多項式曲線擬合法在全調(diào)制比范圍內(nèi)分2 段擬合，在m 為0～0.68 時5 階多項式擬合；0.68～1.15 時6 階多項式擬合。圖5 為3 段4 階多項式擬合，即m 分為0～0.68、0.68～0.849 以及0.849～1.15。圖6 為傅里葉級數(shù)擬合法在全調(diào)制比范圍內(nèi)直接擬合，且為7 階傅里葉級數(shù)展開。

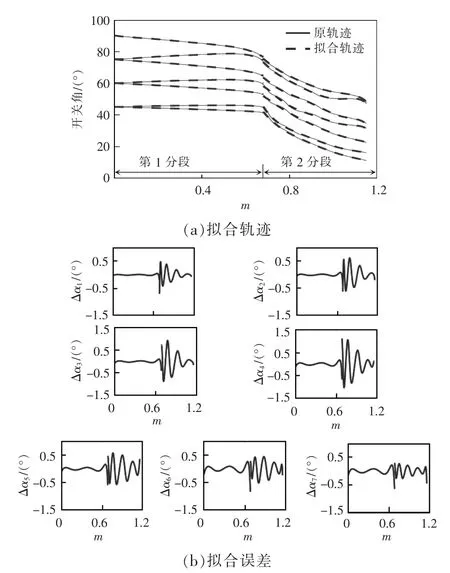
圖4 多項式曲線擬合法：2 分段Fig.4 Polynomial curve fitting method:2 segments

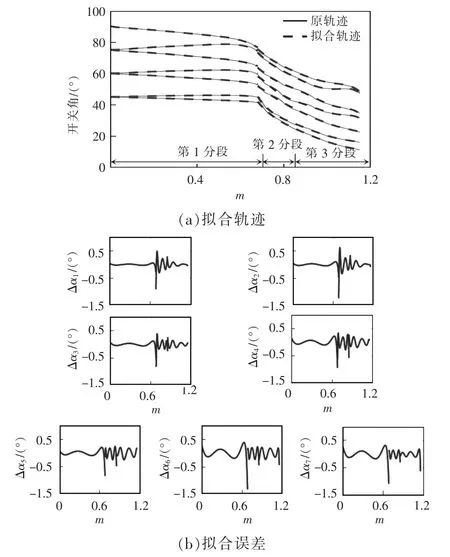
圖5 多項式曲線擬合法：3 分段Fig.5 Polynomial curve fitting method:3 segments

對比圖4 和圖5 可知，多項式曲線擬合法分段越多，總體的擬合誤差越小，但在保證擬合精度的條件下，需經(jīng)過多次實驗來選取滿足擬合精度的分段點，并且不同開關(guān)角個數(shù)的擬合曲線所選取的分段點也不相同，因而實現(xiàn)較為繁雜。由圖4～圖6 對比可得，與多項式曲線擬合法相比，傅里葉級數(shù)擬合法無需分段，在全調(diào)制范圍內(nèi)可直接擬合，在不同的開關(guān)角個數(shù)下無需額外尋找分段點，實現(xiàn)較為簡便。

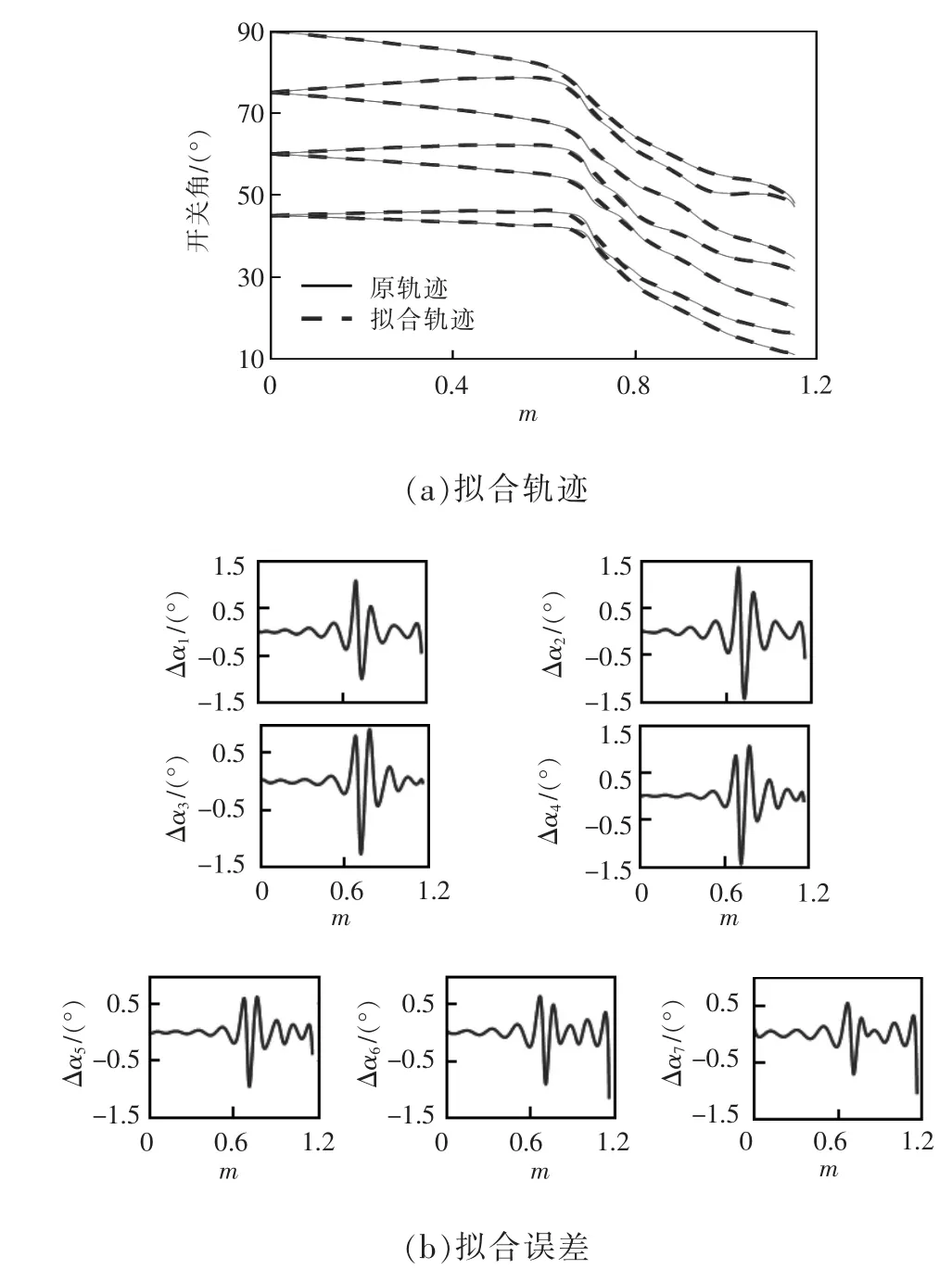
圖6 傅里葉級數(shù)擬合法Fig.6 Fourier series fitting method

3 仿真分析

為驗證傅里葉級數(shù)擬合法的可行性，在Matlab/Simulink 搭建三電平NPC 逆變器仿真模型，驗證當(dāng)開關(guān)角個數(shù)為7，即N=7 時，采用傅里葉級數(shù)擬合法和多項式曲線擬合法的消諧效果，并對比分析。仿真參數(shù)如表1 所示。

表1 仿真參數(shù)Tab.1 Simulation parameters

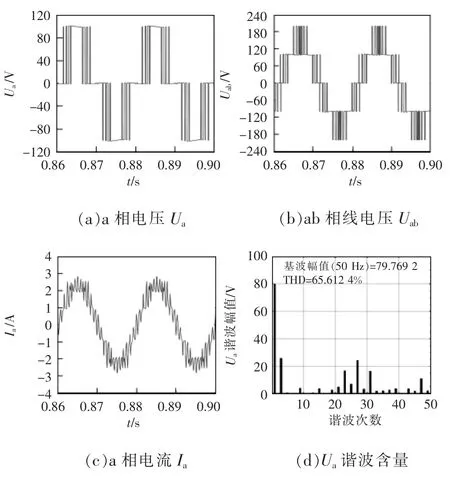
圖7～圖9 分別為不同擬合法下a 相輸出電壓Ua、ab 相線電壓Uab、a 相輸出電流Ia仿真波形及各自對應(yīng)的諧波含量。對比可得，多項式曲線擬合法和傅里葉曲線擬合法基本消除3、5、7、11、13、17 和19 次諧波，并能達到目標(biāo)的調(diào)制比0.8 左右。此外，兩種方法的輸出電流諧波含量基本一致。

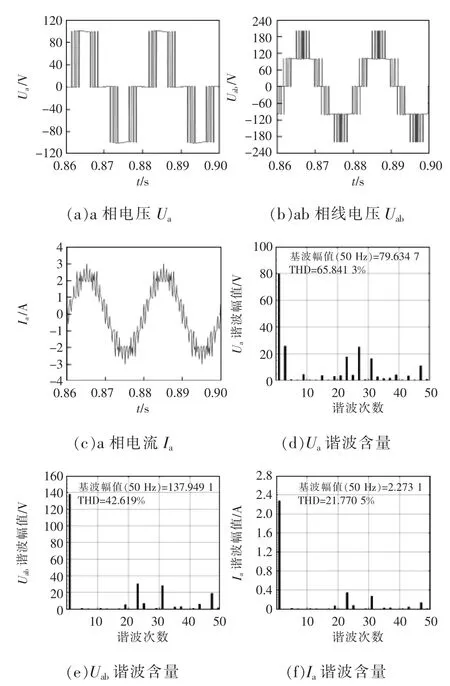
圖7 多項式曲線擬合法：2 分段（仿真）Fig.7 Polynomial curves fitting method:2 segments（simulation）

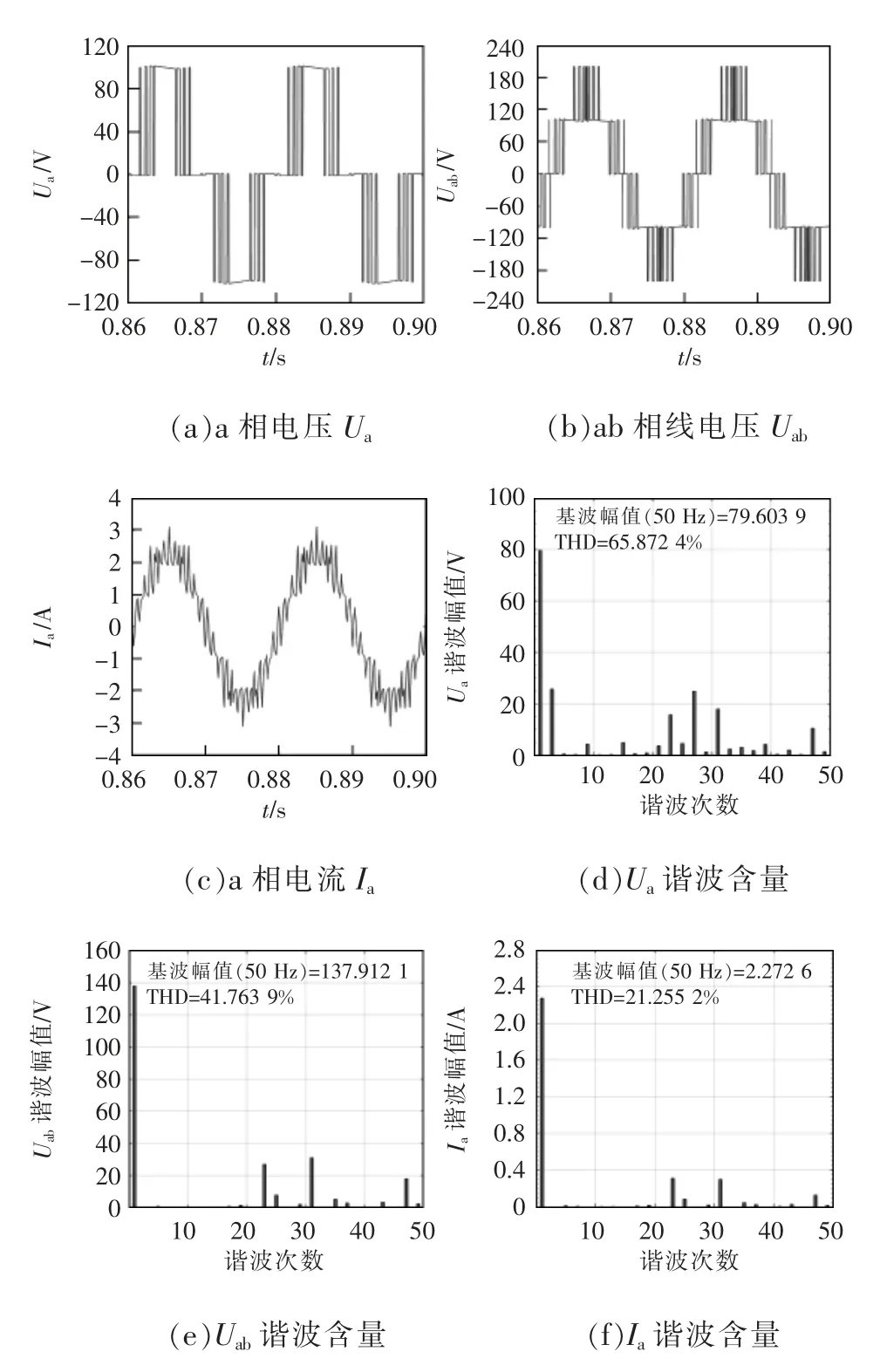
圖8 多項式曲線擬合法：3 分段（仿真）Fig.8 Polynomial curve fitting method:3 segments（simulation）

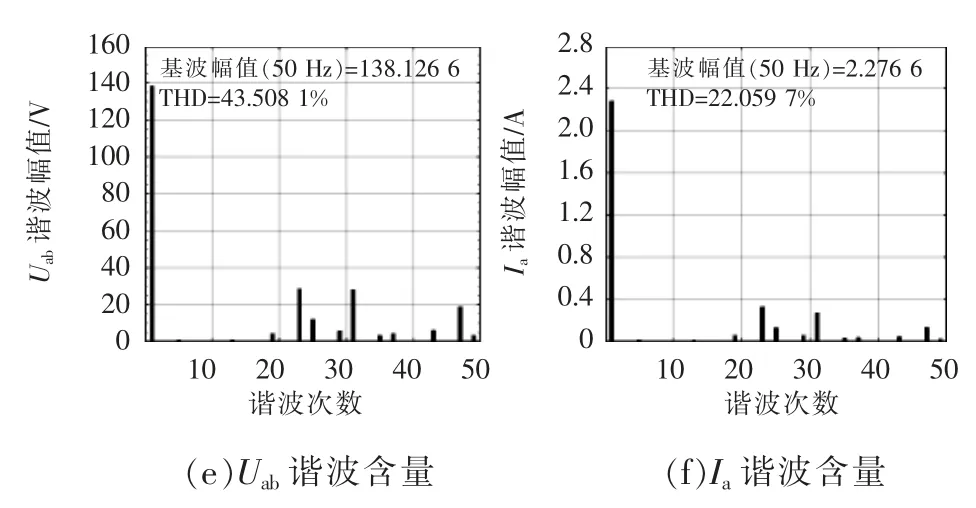
圖9 傅里葉級數(shù)擬合法（仿真）Fig.9 Fourier series fitting method（simulation）

4 實驗驗證

為驗證傅里葉級數(shù)擬合法是否可行，搭建了以TMS320F28335 為核心芯片的三電平NPC 實驗平臺。實驗參數(shù)與仿真參數(shù)一致。

圖10～圖12 分別為不同擬合法下的實驗波形及對應(yīng)的諧波分析。由圖10～圖12 中的實驗波形與圖7～圖9 中的仿真波形對比可知，實驗波形與仿真波形一致。圖10～圖12 中，3 種方式的相電壓基波幅值都在78 V 左右，線電壓基波幅值在133 V 左右，相電流基波幅值在2.2 A 左右，并且5、7、11、13、17和19 次諧波已基本被消除，因而3 種方式諧波消除效果基本一致，驗證了傅里葉級數(shù)擬合法的有效性。由實驗與仿真的諧波含量對比可見，諧波分布一致，但基波幅值偏小，諧波THD 偏大，這是由于實驗中逆變器直流側(cè)為不控整流提供的電壓，非理想直流電壓，故直流側(cè)電壓存在偏差和波動，導(dǎo)致基波幅值偏小，諧波THD 增大。

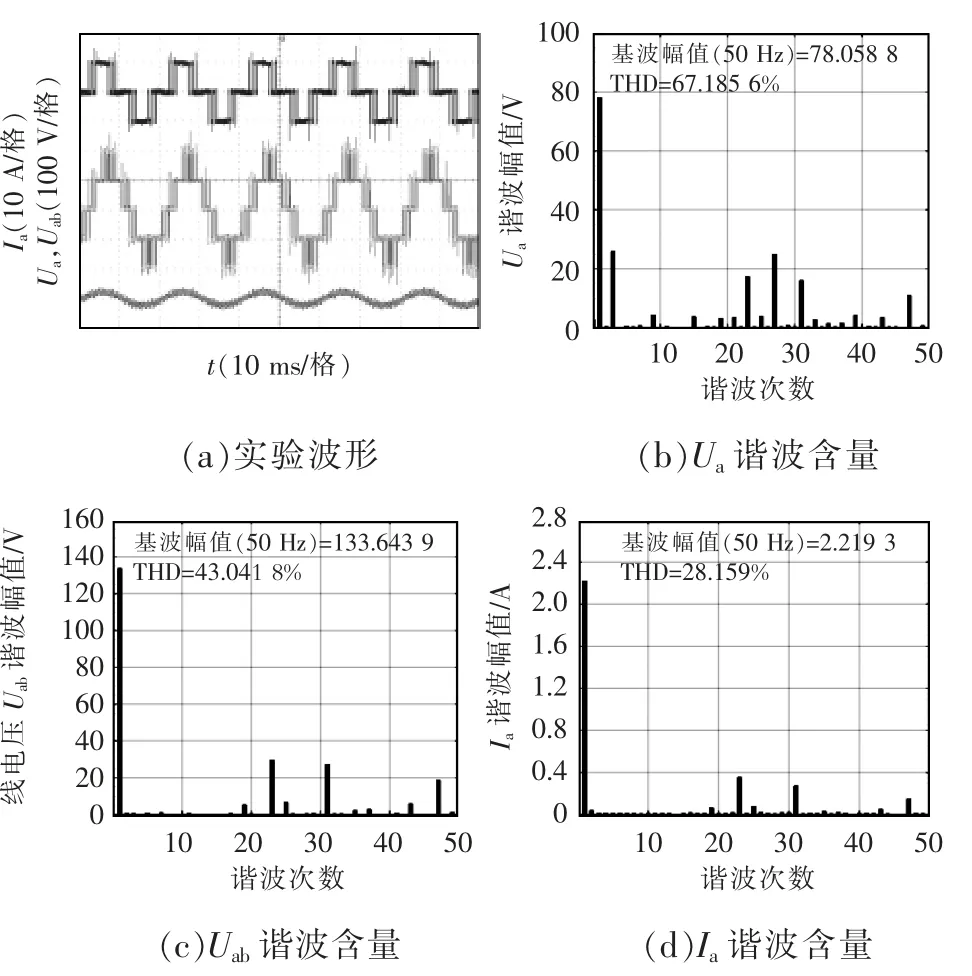
圖10 多項式曲線擬合法：2 分段（實驗）Fig.10 Polynomial curve fitting method:2 segments（experiment）

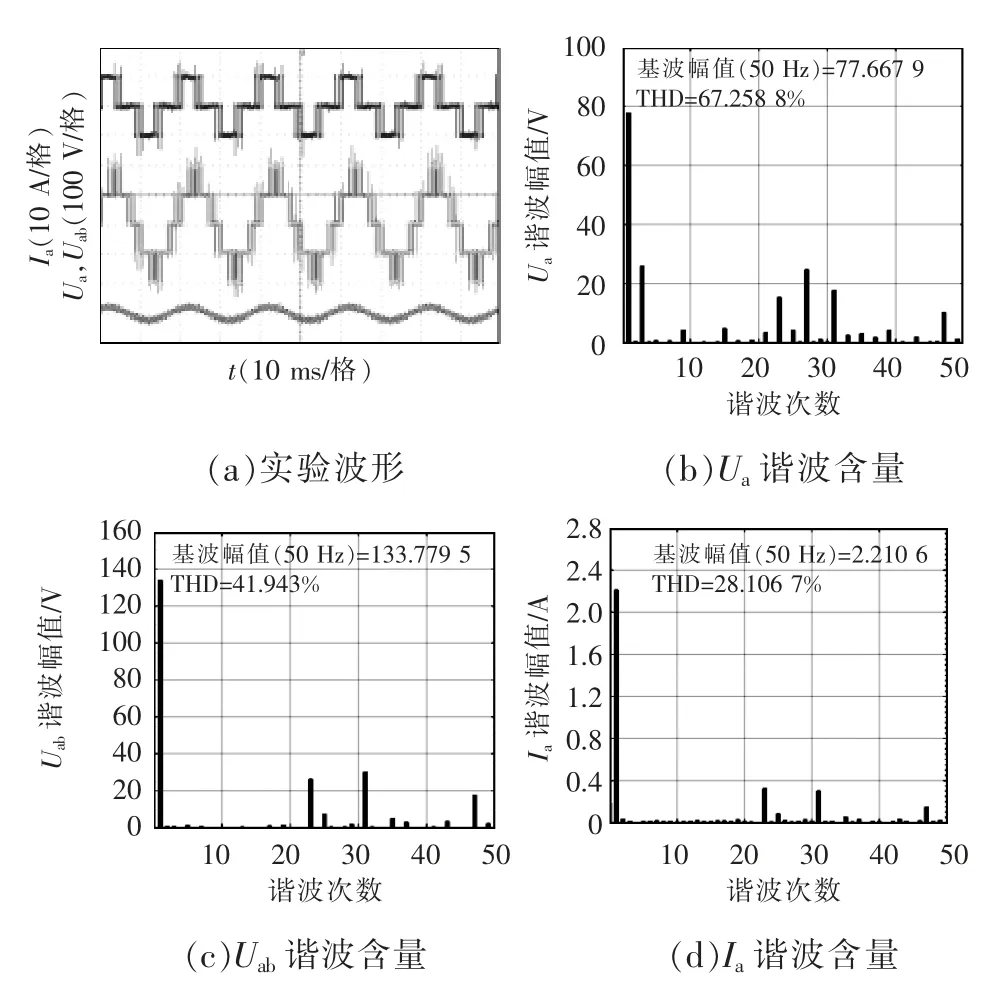
圖11 多項式曲線擬合法：3 分段（實驗）Fig.11 Polynomial curve fitting method:3 segments（experiment）

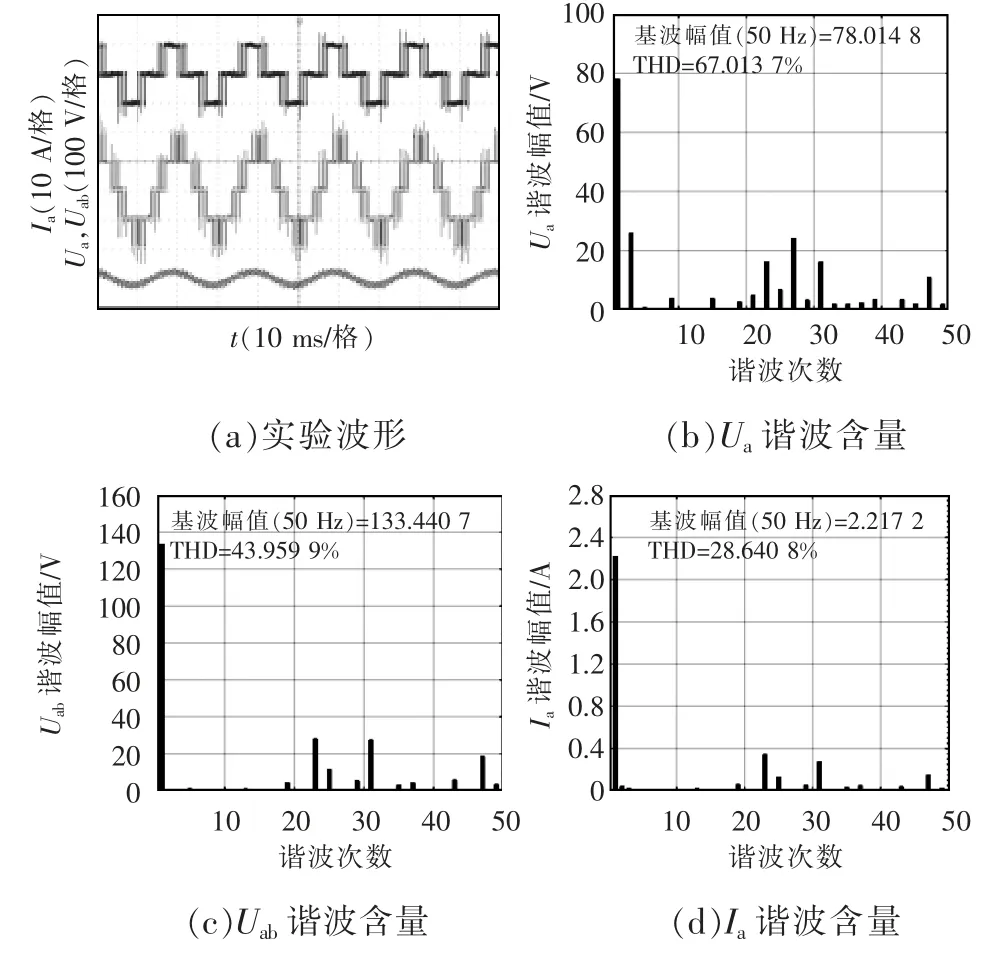
圖12 傅里葉級數(shù)擬合法（實驗）Fig.12 Fourier series fitting method（experiment）

表2 為實驗過程中3 種方法的計算耗時。由表2可以看出，多項式曲線擬合法（3 分段）總的計算耗時最短，而傅里葉級數(shù)擬合法的計算耗時比較長，這是由于傅里葉級數(shù)擬合法中采用了三角函數(shù)，而三角函數(shù)的計算需要耗費一定的時間。但傅里葉級數(shù)擬合法在實現(xiàn)上比多項式曲線擬合法簡便。

表2 實驗計算耗時Tab.2 Time consumption in experimental calculations

5 結(jié)論

本文提出了采用傅里葉級數(shù)擬合實現(xiàn)三電平SHEPWM 開關(guān)角軌跡曲線擬合的方法，通過仿真和實驗驗證傅里葉級數(shù)擬合法的有效性。可以看出，傅里葉級數(shù)擬合法能在全調(diào)制比范圍內(nèi)進行曲線擬合，擬合曲線十分平滑；在滿足擬合精度的情況下，比多項式曲線擬合法簡便，且無需分段。

在實際工程中，采用傅里葉級數(shù)擬合法實現(xiàn)三電平SHEPWM 更為簡便，為三電平及其他電平SHEPWM 的實現(xiàn)提供了一種新的方案。