多電平變換器PWM 控制技術研究現狀綜述及最新進展

朱 宏，李永東，王 奎，QAMAR Muhammad Attique，徐曉娜

（清華大學電機系電力系統及發電設備控制和仿真國家重點實驗室，北京 100084）

多電平變換器因具有可使用低耐壓的器件實現高壓大功率輸出、輸出電壓諧波較少[1]、無需變壓器的特點，近年來在大容量功率轉換領域得到了越來越廣泛地研究和應用。而多電平脈寬調制PWM（pulse width modulation）控制方法是多電平變換器研究領域的核心問題之一。原則上講，基于傳統兩電平逆變器的PWM 控制方法，都可以推廣到多電平逆變器中，目前多電平PWM 方法主要包括載波PWM 和空間矢量脈寬調制SVPWM（space vector pulse width modulation）。由于PWM 控制方法和拓撲是緊密聯系的，而多電平變換器拓撲結構靈活多變，不同的拓撲有不同的特點和要求，因此不斷優化現有PWM 控制方法以滿足不同拓撲的控制要求和性能指標，成為多電平功率變換器PWM 控制策略中一個非常重要的研究內容[2-3]。

一般可以將現有的各種多電平PWM 控制方法按照調制方法的不同分為兩大類，分別是載波PWM和SVPWM 控制方法。載波PWM 控制方法是通過載波和調制波的比較，得到開關脈寬控制信號；SVPWM 控制方法則是通過查表得出參考電壓矢量所對應的開關狀態時序，從而得到對應的脈沖信號。此外，多電平變換器主要分為3 大類：二極管箝位多電平變換器[4]、飛跨電容變換器[5]以及級聯H 橋多電平變換器[6]，針對不同的多電平變換器，多電平PWM控制方法有不同的控制目標和性能指標，但歸納起來，PWM 技術的研究內容主要包括電容電壓平衡控制[7-8]、輸出諧波控制[9]、直流電壓利用率和器件開關損耗控制[10]等。此外，載波PWM 和SVPWM 在一定條件下存在內在聯系。

1 載波PWM

1.1 載波PWM 的基本算法

多電平載波PWM 是兩電平載波PWM 的直接推廣應用，由于多電平變換器有多個載波，根據載波之間的關系可以分為3 種基本調制方法：載波層疊PWM、載波移相PWM 及載波交疊PWM。

1.1.1 載波層疊PWM 和載波移相PWM

載波層疊PWM 及載波移相PWM 調制示意如圖1 所示。根據三角載波之間相位關系的排列不同，載波層疊PWM 可分為3 種不同的多電平載波比較PWM 方法，分別為：同相層疊PD（phase disposition）方式、正負反相層疊POD（phase opposition disposition）方式和交替反相層疊APOD（alternative phase opposition disposition）方式。

以同相層疊方式為例，對比兩電平和三電平變換器下的輸出波形，其波形與諧波分析分別如圖2和圖3 所示。可見，當電平增加，輸出諧波降低。

圖2 兩電平變換器輸出波形Fig.2 Output waveform of two-level converter

圖3 三電平變換器輸出波形Fig.3 Output waveform of three-level converter

多電平載波移相PS（phase-shift）PWM 是指，對于一個n 電平變換器，采用n-1 個不同相位的三角載波與調制波比較，每個載波依次移相360°/（n-1），其PWM 波形如圖1（d）所示。載波移相PWM 和載波層疊PWM 在輸出諧波方面有所不同，由雙邊傅里葉分析可得以下結論。

圖1 載波層疊PWM 及載波移相PWM 示意Fig.1 Schematic of carrier disposition PWM and carrier phase-shift PWM

（1）載波同相層疊法的諧波性能最好，尤其是線電壓諧波性能。交替反相層疊法次之，正負反相層疊式效果最差。

（2）APOD 和PS 方式有相同的諧波性能，前提是在一個基波周期內總的開關次數相同。

（3）在PS 方式下，通過不連續的控制波與移相載波的比較，可以得到類似PD 方式的諧波性能。

1.1.2 載波交疊PWM

在載波層疊PWM 的基礎上，還有特定諧波消除PWM[11]和載波帶頻率變化PWM[12]方法，前者可以降低輸出諧波含量，后者可平衡器件開關次數，提高器件使用壽命，但這2 種方法都存在低調制度下電平退化的問題，即低調制比時，存在一些開關器件始終處于開通或關斷的狀態[13]，開關管得不到完全的利用，而載波交疊CO（carrier-overlapping）PWM 可以提高開關管的利用率。

載波交疊PWM（COPWM）是基于多電平變換器載波之間在豎直方向的位移和水平位移這2 個自由度，提出的新型PWM 方法，目前該方法主要分為3 類，其調制波形如圖4 所示。其中，COPWMA 調制方法輸出的線電壓，無論是諧波頻譜還是諧波含量，都是3 種方法中最好的；COPWM-B 次之；COPWM-C 最差。載波交疊PWM 在低調制度下具有良好的諧波性能，在高調制度下與特定諧波消除PWM 方法基本相同[3]。

圖4 五電平變換器載波交疊PWMFig.4 Carrier-overlapping PWM of five-level converter

1.2 載波PWM 性能指標的優化

1.2.1 輸出諧波性能

1973 年美國學者Patle H S 和Hoft R G 首次提出特定消諧脈沖寬度調制法，通過對輸出電壓的波形進行快速傅里葉變換FFT（fast Fourier transform）分析，得出特定條件下傅里葉展開式，令某些特定次數的諧波為0，得到一個非線性方程組，求解這個方程組，得到開關角，將最終求出的開關角應用于逆變器的控制，則可以在輸出電壓中消除所對應開關角的低次諧波[14]。特定諧波消除法是常用的一種諧波控制方法，但由于需要對非線性方程組求解，計算較為復雜[15]，目前對該方法的研究主要圍繞對求解過程的優化。文獻[16]對載波形狀進行了改進，令每個基波周期內60°～120°，240°～300°之間的載波幅值為0，從而降低了開關頻率，改善了諧波特性。

1.2.2 直流電壓利用率

載波移相PWM 控制方法已成為H 橋多電平電路的標準PWM 控制方法，但載波移相PWM 控制為避免發生過調制，使得輸出電壓幅值較小[17]。針對這個問題，文獻[18]將三次諧波注入法與載波移相結合起來，應用到級聯H 橋型多電平逆變器的控制中，既能擁有良好的諧波抑制特性又能保持較高的直流電壓利用率。載波PWM 控制法在實際應用中加入死區后會引起電流波形畸變，降低電壓利用率，為此文獻[19]提出了一種應用于三電平逆變器的無死區載波層疊PWM 法，采用三重載波生成PWM 信號，通過分析不同工作狀態時的死區效應，推導出功率開關管的導通和關斷規律，根據電壓極性和電流方向確定不同工作狀態下的驅動信號邏輯，實現無死區控制。除此之外，還有開關頻率優化PWM，對于無中線的三相對稱負載系統，在三相逆變器輸出電壓中加入3 的倍數次諧波或直流分量時，對負載電壓波形不會產生影響，利用加入的不同零序分量可以實現載波調制的不同優化目標，如控制電容電壓平衡[20]、提高電壓利用率[21]及降低開關損耗等[22]。

1.2.3 電容電壓平衡控制

為實現飛跨電容型逆變器的電容電壓平衡,文獻[23]提出了一種新型載波同相層疊PWM，該方法利用了飛跨電容型多電平逆變器開關狀態冗余的特點，增加零電平選擇環節，靈活控制零電平向量，實現了三電平飛跨電容逆變器的電容電壓平衡，同時具有載波同相層疊方法的各項諧波性能。文獻[24]提出了一種改進的載波交疊PWM，該方法中每個載波帶中包含所有開關對應的載波，可以實現飛跨電容電壓平衡，且可推廣到N 電平逆變器。文獻[25]為解決四電平中點箝位型變換器的中點電壓平衡問題，提出了一種新型的載波交疊PWM，該方法可在全調制指數和功率因數范圍內實現中點電壓平衡，其載波波形如圖5 所示，其中Cr1、Cr2、Cr3為相位相同，幅值不同的三角載波。該調制方法下的3個母線電容電壓的偏移量分別為ΔUd1x、ΔUd2x和ΔUd3x，其表達式為

圖5 改進載波交疊PWMFig.5 Improved carrier-overlapping PWM

2 SVPWM

SVPWM 易于數字化實現，特別是多電平SVPWM 技術具有直流電壓利用率高、開關損耗低等優點，在開環和閉環控制系統中都得到廣泛應用。

2.1 SVPWM 的基本控制方法

該類方法是從兩電平SVPWM 直接推廣而來的。SVPWM 算法的基本原理就是基本電壓矢量在一定的時間作用下合成得到輸出電壓矢量，用多邊形無限逼近于圓，從而使電機獲得幅值恒定的圓形磁場，即正弦磁通[26]。在控制過程中，需要先判斷參考電壓矢量所在位置，根據最近三矢量法選擇基本電壓矢量，并根據伏秒平衡原理計算各矢量作用時間，然后根據基本矢量與開關狀態的對應關系，并結合其他要求，確定所有輸出的開關序列及其輸出形式。但是，隨著電平數的增多，可選擇的多電平空間矢量也很多，同時由于在直角坐標系下需要求解三角函數，計算量較大。

2.2 SVPWM 控制的優化

2.2.1 非正交坐標系下的SVPWM 算法

非正交坐標系包括g-h 坐標系（60°坐標系）和K-L 坐標系（120°坐標系）。g-h 坐標系和K-L 坐標系的三電平空間矢量如圖6 所示[27]。

圖6 g-h 坐標系和K-L 坐標系下三電平空間矢量Fig.6 Three-level space vector in g-h and K-L coordinate systems

非正交坐標系下SVPWM 算法的具體實現步驟如下。

步驟1選擇合成電壓矢量。以K-L 坐標系為例，設參考電壓為Vref，VrL、VrK為Vref在K-L 坐標系下的分量。分別對VrL、VrK向上取整和向下取整得到4 個坐標，在坐標軸上的位置如圖7 所示。

圖7 合成電壓矢量位置示意Fig.7 Schematic of composite voltage vector position

步驟2根據Vref所在區域，選擇最近的3 個電壓矢量。判斷其所在區的數學表達式為

式中：K=int（VrK）；L=int（VrL）。

步驟3計算矢量作用時間。設Vref在Ⅰ區，則選擇的基本矢量為Va、Vb、Vc，由伏秒平衡可得各矢量作用時間為

式中，Ta、Tb、Tc為基本矢量Va、Vb、Vc的作用時間。

步驟4確定輸出開關狀態。三相開關的輸出狀態為

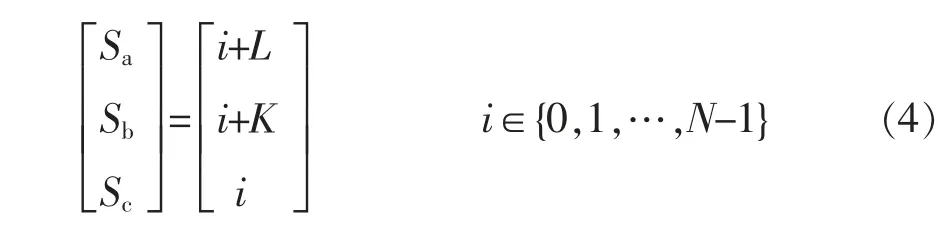
可根據不同的控制目標選擇開關狀態。

文獻[28]提出了一種采用平面三相虛坐標的方法實現多電平PWM 控制的通用算法，將SVPWM 控制分為輸出電壓合成和通過零序電壓進行控制兩方面，其中ja、jb、jc為虛坐標軸，由a、b、c 軸逆時針旋轉90°可得。一方面體現了三相對稱的特點，便于數學分析；另一方面計算方便，能適用于不同拓撲的各種應用場合。除此之外，為滿足三相四線制四橋臂逆變器的控制需求，產生了三維空間坐標系下的SVPWM 控制算法，將空間矢量的三相定義擴展為“四相”，將第4 相的零線輸出放在與原有平面垂直的軸上，從而構成了“三維”PWM 方式[29]。

2.2.2 電容電壓控制

空間矢量圖中包括長矢量、中矢量、小矢量和零矢量，其中中矢量和小矢量作用時的輸出電流會造成中點電壓偏移，當工作條件涉及較大的調制指標和有源負載電流時，傳統的SVPWM 無法實現具有較多電平（N>3）的中點箝位型變換器的電壓平衡。為此，文獻[30]提出了一種虛擬矢量合成的方法，在理論和實驗中證明了此方法既可以實現中點電壓平衡控制，又避免了較高的dv/dt，在空間矢量的基礎上定義了以下2種虛擬矢量。

（1）虛擬中矢量。中矢量的輸出電流會造成中點電壓偏移，將1 個中矢量和2 個小矢量合成為虛擬中矢量，3 個矢量輸出電流分別為ia、ib、ic。令每個矢量的作用時間相等，則io=ia+ib+ic=0，虛擬中矢量對中點電壓無影響，因此在理論上可以完全控制中點電壓平衡。

（2）虛擬長矢量。虛擬長矢量由1 個長矢量和2個短矢量合成，2 個短矢量的占空比相等且小于長矢量的占空比，故虛擬長矢量對中點電壓無影響，且dv/dt 更小。

在此基礎上，文獻[31]提出了最近三虛擬空間矢量PWM，并給出了新的虛擬矢量定義方法及選擇標準，合成原則為

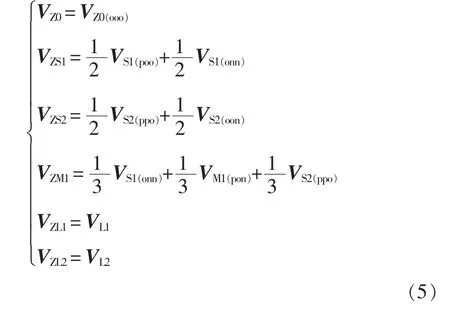
式中：矢量VZ0、VS1、VS2、VZM1、VZL1、VZL2均為虛擬空間矢量；VZ0、VS1、VS2、VM1、VL1、VL2為基本 電壓矢量；p、o、n 分別表示三相輸出電平為Vdc/2、0、-Vdc/2。各虛擬矢量在一個采樣周期內輸出的中點電流的有效值為0，故各虛擬矢量對中點電壓無影響，不會造成中點電壓波動。

虛擬矢量控制在理論上可以實現對中點電壓平衡的完全控制，但在實際應用中，在計算誤差及干擾下，由于累計效果，可能造成中點電壓波動。針對這個問題，文獻[32]基于三電平中點箝位型變換器，提出了一種變虛擬空間矢量，對虛擬小矢量引入調節因子，通過檢測中點電壓波動情況，調整下一周期虛擬矢量的作用時間，從而彌補上一周期的中點電壓偏差量，實現中點電壓平衡控制。

采用傳統虛擬空間矢量PWM 理論上可以實現直流電容電壓平衡的全控制，但增加了計算量和復雜度。四電平NPC 變換器采用空間矢量PWM 時，每個扇區包含9 個三角形，而虛擬空間矢量PWM將一個扇區的三角形數增加到13 個，這將增加計算量和實現的復雜度。此外，其增加了開關頻率，惡化了逆變器的輸出波形。

為實現四電平二極管箝位變換器的中點電壓平衡，同時減少計算量，文獻[33]提出了一種簡化虛擬空間矢量PWM，該法可將四電平空間矢量圖簡化為三電平空間矢量圖。對虛擬矢量的定義為

通過對傳統虛擬矢量進行合成再定義，四電平空間矢量得到了很大簡化，每個扇區僅有4 個三角形，大大簡化了運算量，降低了算法的復雜度。

四電平簡化虛擬空間矢量算法已在實驗中得到驗證，圖8 為調制比m=0.9 時四電平箝位型變換器在該算法下的相電壓、線電壓、相電流及電容電壓的波形。

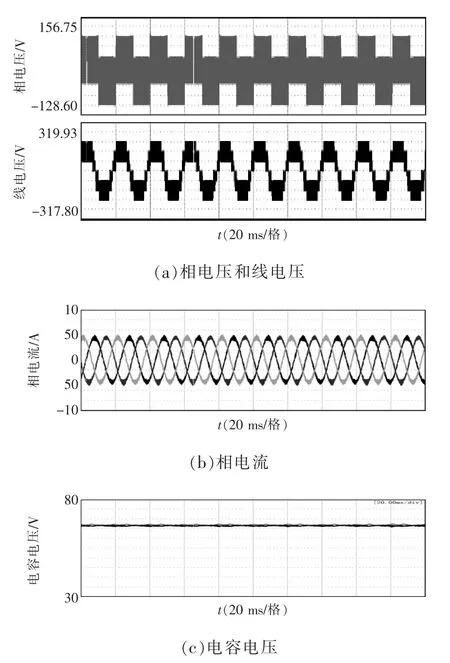
圖8 m=0.9 時四電平NPC 簡化虛擬空間矢量下的波形Fig.8 Waveforms of four-level NPC simplified virtual space vector when m=0.9

3 SVPWM 與載波PWM 統一理論

由于SVPWM 和載波PWM 均為基于一個采樣周期內電壓積分等效的思路，故二者在本質上是等效的。文獻[34]以二極管鉗位型五電平逆變器為例，采用調制波分解策略，在常規的三角載波PWM 的各相調制波中加入一個零序分量就可得到和SVPWM 完全相同的輸出波形，從而推導出任意電平8 段以上SVPWM 開關序列與載波PWM 的統一理論。以該方法為基礎，文獻[35-36]分別對飛跨電容型變換器和有源中點箝位變換器，提出了改進的調制波分解方法，完善了不同拓撲結構下的SVPWM 與SPWM 的統一理論，在此基礎上，系列結合SPWM 與SVPWM 優點的優化PWM 算法被提了出來。

文獻[37-38]利用SVPWM 與載波PWM 的聯系，提出了一種基于載波SPWM 與SVPWM 混合控制的三電平逆變器中點電位平衡策略，實現了不同負載功率因數變化下的中點電壓平衡。文獻[39]以SPWM對稱規則采樣的波形與SVPWM 對稱七段式波形相似為出發點，由SPWM 的調制隱函數推導出SVPWM 的調制隱函數，并對SVPWM 的調制隱函數進行簡化分解，得出簡化的SVPWM 算法，該算法直接利用三相參考電壓瞬時值計算PWM 信號的開關狀態切換時間，不需進行坐標變換、三角函數運算、扇區判斷和有效矢量作用時間的計算。

通過理論分析，SVPWM 可通過向SPWM 注入特殊零序分量得到，二者在本質上是一致的，只是在實現方法上有所不同。

4 結語

本文主要介紹了多電平載波PWM 和SVPWM控制方法，在此基礎上，針對不同拓撲結構、不同控制目標，介紹了多種優化控制方法。多電平變換器具有廣泛的應用前景，電平數不斷增加，多電平變換器的拓撲結構也在不斷地優化，多電平PWM 算法的優化目標和計算量隨之增加，而多電平SVPWM 與SPWM 統一理論的提出，可對算法進行一定的簡化，后續可在該理論的基礎上進一步研究2 種PWM 方法數字實現的統一，將SPWM 實現簡單和SVPWM 易數字化的優點結合起來。