中考數(shù)學(xué)專題復(fù)習(xí)中支架式教學(xué)策略的運用
——以“二次函數(shù)綜合題之特殊角存在性問題”為例
李月明
(廣東省江門市蓬江區(qū)紫茶中學(xué) 529000)
一、基本概術(shù)及適用性
支架式教學(xué)認為:為學(xué)習(xí)者建構(gòu)對知識的理解提供一種概念框架,這種框架中的概念是為發(fā)展學(xué)習(xí)者對問題的進一步理解所需要的.支架式教學(xué)模式下,教師事先要把復(fù)雜的學(xué)習(xí)任務(wù)加以分解,以便于把學(xué)習(xí)者的理解逐步引向深入.
中考數(shù)學(xué)專題復(fù)習(xí)是中考數(shù)學(xué)總復(fù)習(xí)的關(guān)鍵環(huán)節(jié),是培養(yǎng)學(xué)生靈活運用基礎(chǔ)知識、提升綜合能力的核心過程.傳統(tǒng)的復(fù)習(xí)教學(xué)流程是教師根據(jù)考綱要求,指定學(xué)生完成相應(yīng)的考題,學(xué)生多是模仿,一知半解,難以內(nèi)化成自身的能力與素養(yǎng).支架式教學(xué)模式突破傳統(tǒng)弊端,關(guān)注學(xué)生的起點與認知特點,指引教師根據(jù)新課程標(biāo)準(zhǔn)的培養(yǎng)目標(biāo),細分學(xué)習(xí)任務(wù),設(shè)置個性化學(xué)習(xí)支架,學(xué)生借助學(xué)習(xí)支架自主向?qū)W習(xí)的廣度和深度發(fā)展,如何提高中考專題復(fù)習(xí)的質(zhì)量與效益,這與中考數(shù)學(xué)專題復(fù)習(xí)的目標(biāo)需求是一致的.
二、課例運用分析
為探索支架式教學(xué)模式在中考數(shù)學(xué)專題復(fù)習(xí)的教學(xué)實踐經(jīng)驗和理論指導(dǎo),結(jié)合已有的系列專題復(fù)習(xí)課設(shè)計與實施運用的探索,筆者以2018年廣東中考第23題為主線,開展《中考專題復(fù)習(xí)——二次函數(shù)綜合題之特殊角存在性問題》專題復(fù)習(xí)教學(xué)實踐,取得較好的效果.
1.課例設(shè)計片段
活動一、搭腳手架構(gòu)建模型
(1)直線y=x+m過點C(0,-3),則m的值為____,則直線的解析式為____;該直線與x軸交于點B,則點B的坐標(biāo)為____,∠OCB=____°.

(2)如圖1,在第(1)題的條件下,是否存在x軸上的一個點A,使得直線AC與直線BC的夾角∠ACB=15°,則符合要求的點A有____個;此時∠ACO的度數(shù)為____;則點A的坐標(biāo)是____.
活動二、展開支架應(yīng)用模型
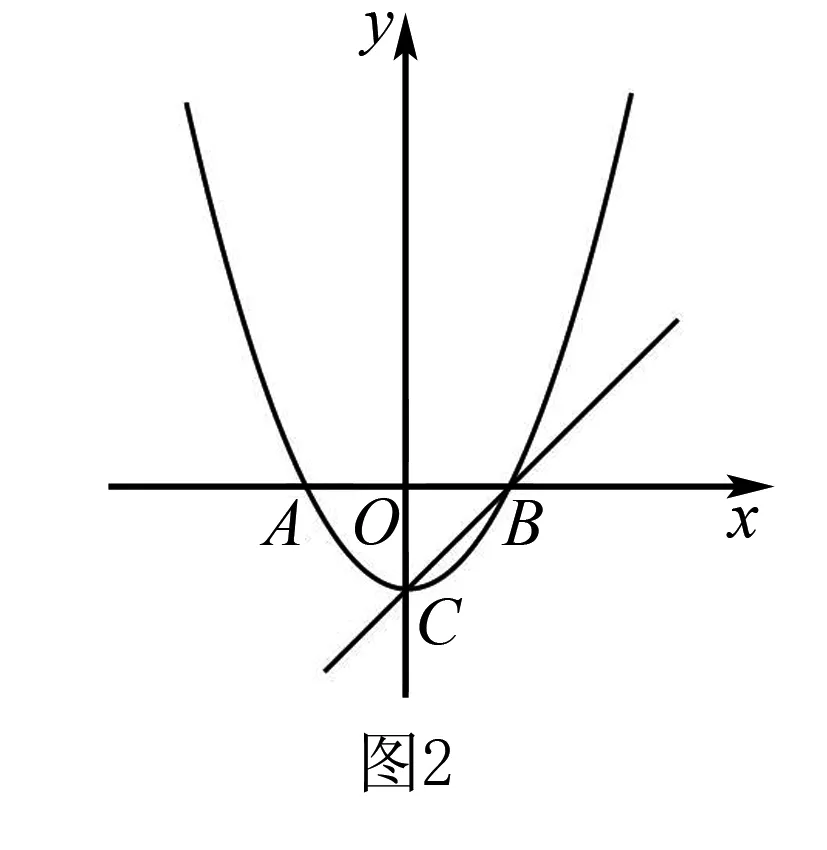
【2018廣東中考23題】如圖2,已知頂點為C(0,﹣3)的拋物線y=ax2+b(a≠0)與x軸交于A,B兩點,直線y=x+m過頂點C和點B.
(1)求m的值;
(2)求函數(shù)y=ax2+b(a≠0)的解析式;
(3)拋物線上是否存在點M,使得∠MCB=15°?若存在,求出點M的坐標(biāo);若不存在,請說明理由.
活動三、拓展支架巧用模型

(1)求拋物線的解析式;

【設(shè)計實施說明】2018年廣東中考第23題的(1)(2)中考查代入點坐標(biāo)求函數(shù)的常數(shù)項、待定系數(shù)法求函數(shù)解析式等知識點,是常見的考點,也是當(dāng)前學(xué)生已經(jīng)熟悉掌握的內(nèi)容.基于中考專題復(fù)習(xí)課的特點,課程設(shè)計融合信息技術(shù)輔助教學(xué),把這部分內(nèi)容的復(fù)習(xí)鞏固設(shè)置到課前,以突出本專題復(fù)習(xí)的重點.問題(3)中考查點的存在性問題,其本質(zhì)是構(gòu)造模型,分析特殊角的加減,這是學(xué)生認知的最近發(fā)展區(qū).為分散難點,有效突破,依據(jù)課時目標(biāo)與學(xué)情搭建腳手架,由淺入深地幫助學(xué)生梯度推進,快速接近模型中心.學(xué)生通過學(xué)習(xí)支架的輔助,對自主探究2018年廣東中考第23題有充足的準(zhǔn)備,能獨立思考解決問題.改編2018湖南岳陽中考24題,既檢測學(xué)生對特殊角存在性問題理解的程度,又引導(dǎo)學(xué)生問題思考過程合理遷移,促進思維向高階拓展.
三、教學(xué)策略分析
存在性問題是指判斷滿足某種條件的事物是否存在的問題.中考視角下,這類問題常以動點問題為背景,知識覆蓋面較廣,綜合性較強,題目構(gòu)思非常精妙,解題方法靈活,對學(xué)生分析問題和解決問題的能力要求較高.圍繞存在性問題專題復(fù)習(xí)的系統(tǒng)性目標(biāo),依據(jù)學(xué)情搭建問題串學(xué)習(xí)支架,深化信息技術(shù)輔助教學(xué),能有效促進學(xué)生自主建構(gòu)知識體系,提高分析問題、解決問題的能力.本節(jié)課主要運用以下幾種支架式教學(xué)策略,幫助學(xué)生自主攻克難點,掌握方法.
1.基于問題化的支架式教學(xué)法
課程目標(biāo)是歸納二次函數(shù)綜合題中特殊角的存在性問題的解法技巧,體會運用數(shù)形結(jié)合、分類討論等數(shù)學(xué)思想合理建模的過程.2018年廣東中考第23題考察了代入求值、待定系數(shù)法求函數(shù)解析式及二次函數(shù)綜合題中特殊角的存在性問題,是二次函數(shù)綜合題的典型考察內(nèi)容.以中考真題為母題,把基礎(chǔ)考查內(nèi)容設(shè)計為螺旋式思維遞進問題串支架,設(shè)置于母題的探究前,過程中同時滲透中考命題角度的分析、明晰能力培養(yǎng)方向.學(xué)生帶著問題任務(wù)進行積極的自主學(xué)習(xí),借助問題串支架輕松“上架”,觸動學(xué)生對專題復(fù)習(xí)的基本知識由表及里,由淺入深地進行自主構(gòu)建,夯實基礎(chǔ).
2.基于信息化的支架式教學(xué)法
二次函數(shù)綜合題中特殊角的存在性問題的基本模型是角的加減.課例中2018年廣東中考第23題以二次函數(shù)與一次函數(shù)綜合模型為背景,分析復(fù)雜的函數(shù)綜合圖象,厘清解題突破口是角的加減,這既是重點,也是難點.在確定學(xué)生對函數(shù)模塊認知的最近發(fā)展區(qū)之后,鎖定核心模型,運用網(wǎng)絡(luò)畫板的動畫展示功能,創(chuàng)設(shè)信息技術(shù)輔助學(xué)習(xí)支架,由一般到特殊地刻畫數(shù)學(xué)模型的構(gòu)建過程.學(xué)生通過觀察動態(tài)演示、手動比較等活動,深刻理解直線與兩坐標(biāo)軸的夾角為45°的特殊事實,領(lǐng)悟15°角的存在性問題轉(zhuǎn)化為30°和60°特殊角,本質(zhì)是角的加減模型,從而全面思考、分類討論所有符合要求的情況.透過網(wǎng)絡(luò)畫板的信息技術(shù)輔助支架,直觀、形象、快捷地突破難點,喚醒學(xué)生學(xué)習(xí)認知的已有經(jīng)驗,促進學(xué)生的聯(lián)想與想象,開發(fā)其潛在動機資源,促進學(xué)生所學(xué)知識的有效遷移,綜合運用知識構(gòu)建模型分析問題、解決問題.
3.基于圖式化的支架式教學(xué)法
為拓展學(xué)生既有水平,提高中考數(shù)學(xué)專題復(fù)習(xí)的教學(xué)質(zhì)量,根據(jù)教學(xué)需要,有目的地改編中考真題,構(gòu)建可視的圖式學(xué)習(xí)支架,針對性地引導(dǎo)學(xué)生扎實地對相關(guān)概念的理解和綜合應(yīng)用,把抽象的數(shù)學(xué)知識直觀化、形象化,使學(xué)生快速地基于已有的經(jīng)驗圖式構(gòu)建新圖式,觸類旁通地解決此類問題則是教學(xué)的關(guān)鍵.支架性地實現(xiàn)數(shù)學(xué)概念在學(xué)生大腦中系統(tǒng)性地構(gòu)建,深化理解,達成提高學(xué)生理解能力與應(yīng)用能力的雙客觀效果,支架性地幫助學(xué)生理解數(shù)學(xué)概念是可選擇的重要的策略性選項之一.從而促進學(xué)生從一個能力水平向另一個更高的能力水平過渡,發(fā)展高級心理機能,成為獨立、能動的學(xué)習(xí)者.

