淺談初中數學利用建系法巧解幾何題

曾鈺玲

(福建省漳州實驗中學 363000)

一、建系法

建系法作為函數的開端，也有一定的難度.不會建系，坐標寫不清楚，中點坐標公式、兩點距離公式不會應用等等的問題，都會使得一部分學生對建系法望而卻步.然而仍然不能否認建系法對解題的幫助.

因此，本文挑選一些幾何題，對比幾何法解題和建系法解題，能更直觀的理解幾何法與建系法.從而加深對建系法的理解，學會使用建系法巧解幾何題.

解題過程中可能會用到中點坐標公式、兩點坐標公式，在此先作補充：

二、例題講解

例1如圖1，正方形ABCD與正方形CGEF的邊長分別是2和3，且B，C，G三點在同一條直線上，M是線段AE的中點，連接MF，則MF=____.

解法一幾何法

對于學生來說，幾何題用幾何法解，是最直接的思路，而幾何法通常需要作輔助線，這就是幾何法的難點所在.

解延長AD，與FM的延長線交于點Q(如圖2)

因為M是線段AE的中點，所以AM=EM

又因為四邊形ABCD與CGEF都是正方形，

所以AD∥EF

所以∠AQM=∠EFM，∠MAQ=∠MEF

所以△FME≌△QMA(AAS)

所以MQ=MF

因為∠FDQ=90°，FD=FC-DC=1

DQ=AQ-AD=FE-AD=1

所以△FDQ是等腰直角三角形，腰長為1

解法二建系法

思路分析要求MF的長，則需要M點坐標和F點坐標，F點坐標易知，所以只需求M點坐標即可.而M點是AE中點，所以只需知道A、E點坐標即可，A、E點坐標易知.(如圖3)

解以C為坐標原點，BC所在直線為x軸，建立平面直角坐標系.則A(-2，2)，E(3，3)

因為M是線段AE的中點，

因為F(0，3)

所以由兩點距離公式得

從以上解題過程可以很直觀看出用建系法解題相對于幾何法來說，確實簡單很多，書寫上也更簡潔.減少了學生最常出錯的輔助線描述過程，減少了思考量.思路也更為直接.

建系法有時還會涉及到求函數解析式和交點坐標，也是學生非常容易出錯的難點.

例2如圖4，已知正方形ABCD的邊長為5，E，F分別是邊CD、AD的中點，BE、CF交于點P，求AP的長.

解法一幾何法

解延長PF，與BA延長線交于點M(如圖5)

因為ABCD是正方形，且E，F是中點

所以△BCE≌△CDF

所以∠PBC=∠FCD

因為∠PBC+∠BEC=180°-∠BCE=90°

所以∠FCD+∠BEC=90°

所以∠EPC=90°，所以∠FPB=90°

因為F是AD中點

所以△AFM≌△DFC

所以AM=DC

所以A是BM中點

所以PA為RT△BPM中斜邊BM上的中線

解法二建系法

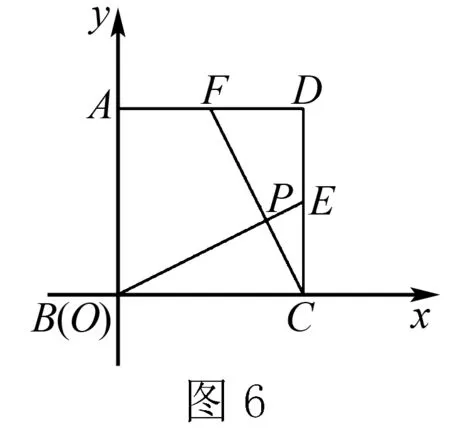
思路分析則要求AP的長，需要知道A點坐標和P點坐標，A點坐標易知，則只需求P點坐標即可.而P點是BE與CF的交點，則需要求出BE和CF所在直線的表達式即可.(如圖6)

解以B為原點，BC所在直線為x軸，AB所在直線為y軸，建立平面直角坐標系.C(5，0)，B(0，0)

因為E、F是CD、AD中點，所以E(5，2.5)，F(2.5，5)

BE、CF交點坐標P為(4，2)

對比幾何法與建系法會發現，幾何法涉及到的知識點較多，并且不同的題目會涉及到不同的知識點，但建系法則比較單一，即使在不同的題目內，幾個公式也可以反復用.

以上兩個例子是在正方形的背景下，而建系法絕不僅僅能用于正方形，接下來將介紹建系法在其他題型的應用.(注：以下只展示建系解法，不再展示幾何解法)

例3如圖7，△ABE與△DBC都是等腰直角三角形，BC=2，AB=4，G、H分別是CD、AE中點，則GH=____.

思路分析要求GH的長，需要G、H兩點坐標，G、H是CD、AE中點，A、E、C、D坐標易知，因此此題用建系法做非常簡單.

解以B為原點，BE為x軸，AB為y軸，建立平面直角坐標系(如圖8)A(0，4)，E(4，0)，C(-2，0)，D(0，2)

所以G(-1，1)，H(2，2)

從解題思路及計算過程均可看出，用建系法解幾何題，難度下降.因此平時上課時，老師也可以有意識的引導學生用建系法解決較難的幾何題.

總結數學本身是一門思維非常靈活的學科，如何在數學的學習過程中提高學生對數學概念的理解，促進發散性思維的提升，從而形成良好的認知結構，是作為一線數學教師需要不斷學習的一種能力.

對于初中學生來說，函數是一個難點，但是如果函數學好了，也能成為一把利劍，幫助學生提高解題能力.本文只研究了平面直角坐標系對解決平面幾何問題的幫助，而高中階段，空間直角坐標系對于立體幾何的幫助也是很大的.并且，建系法不僅在解幾何題方面有幫助，在提高學生數形結合能力方面的幫助更大.作為一線教師，平常的解題過程可以多向學生灌輸建系法，讓學生在多次練習中熟悉，并且掌握建系法，最終實現能用建系法解題的目的.