風速對蒲公英種子尾渦的影響

鮑雯昱，李 威，岳海龍，邱福生，何天寶

(1.沈陽航空航天大學 航空宇航學院，沈陽110136；2.中國南方航空股份有限公司 沈陽維修基地，沈陽 110136)

在人類發明飛行器以來，隨著科學水平的進步，越來越多的飛行方式諸如固定翼、多旋翼、撲翼等出現在生活里，飛行原理大多來源于人類對自然的認知，仿制自然界鳥類、昆蟲等飛行方式得出[1-2]。仿生學的發展為航空航天技術的突破和復雜問題的解決提供了一條有效的途徑和最大的可能。蒲公英是十分常見的一種植物，在花期時它的絨毛種子借著風力向四面八方傳播。在傳播種子時，蒲公英有一種巧妙的飛行機制，使它在保持高度方面的效率是人類降落傘的4倍左右[3-4]，從而借助風力飛出幾百米甚至上千米遠[5-6]。近年來，國外一些科學家開始研究蒲公英這種獨特的飛行機制，他們構建了一個垂直的風洞，可以使種子在一個穩定的高度上盤旋，然后把蒲公英種子放進風洞，嘗試用長時間曝光攝像和高速成像來觀察種子周圍的氣流變化，發現蒲公英種子上方的空氣形成了一個特殊的渦環。這種渦環是由其種子毛茸茸的冠毛所形成的一種環形的氣泡，就像漩渦一樣。這種渦環形成在蒲公英種子的上方，與種子本體分離[7-9]。冠毛本身運動產生的氣流和在種子周圍的氣流之間形成了壓力差，產生了渦流環流。渦流環流在增加了空氣阻力的同時，也讓種子像降落傘一樣減緩了下降速度。蒲公英種子要飛行較遠的距離，還需要保持在一個比較穩定的飛行高度。所以渦環還有一個非常重要的特點，可以穩定地保持在蒲公英種子上方固定距離的位置[10]。不僅如此，蒲公英冠毛的孔隙度似乎受到精確地調控以穩定渦環。研究團隊認為，正是這一原理，保證了蒲公英長遠穩定的擴散飛行[11]。

CFD技術自 20 世紀 60 年代隨計算機技術的不斷進步而迅速發展，如今已深入到包括航空、航天、船舶、水利、冶金、建筑、化工等工程領域的各個方面，取得了巨大的成就。航空工業界是最早應用和發展 CFD 技術的領域，在半個多世紀的時間里，形成了一套行之有效的CFD 技術應用方式，充分合理地利用了CFD的技術優勢，有效縮短了技術研發與型號研制的周期。在當今航空領域迅猛發展的形勢下，CFD 技術展現出巨大的應用價值和發展潛力[12]。

計算流體力學CFD理論與數值求解方法的不斷拓展和革新，使得這一學科在越來越多的領域得到了廣泛應用。為之提供強有力支持的高性能計算技術的發展，從更大程度上促進了CFD技術的發展及應用。CFD技術帶來的增益不僅體現在工程應用上，也為探索流動的演化機理和發現新的流動現象提供了十分有效的手段，更進一步豐富了計算流體動力學的研究內容[13]。

本文使用CFD方法對蒲公英簡化模型進行數值模擬，是因為CFD方法可以低成本、高效率完成大量的實驗。低微速風洞的構建具有很大困難，很難保證較小速度梯度的準確性，使用CFD方法可以快速找到渦流出現的速度值，并分析不同速度下的氣流特性。

本文使用CATIA對蒲公英模型進行簡化和建立，運用CFD方法對簡化蒲公英種子模型進行數值模擬,通過改變風速觀察對蒲公英種子模型的影響。該項實驗的目的是對蒲公英種子產生的特殊尾渦進行分析，分析風速對流經蒲公英種子的氣流的速度壓力等特性從而驗證蒲公英種子這種獨特的飛行機制。

1 計算模型

蒲公英種子的絨毛結構極其復雜，每個種子上有幾百根細細的絨毛[14]，絨毛尖端又有肉眼難以看見的冠毛[15]，使建模較為困難，因此將模型簡化為中心實體，即外部均勻分布細長桿的多孔圓盤來替代蒲公英種子的結構。根據自然界蒲公英種子的孔隙度[16]，確定圓盤的結構如圖1所示，圖2為自然界蒲公英種子的絨毛結構。

圖1 多孔圓盤模型

圖2 自然界蒲公英種子

在圓盤外建立圓柱形流場如圖3所示。

圖3 外流場計算域

高質量的貼體、正交和合理分布的網格將有助于提高計算效率，并對數值模擬的精度有重要影響[17-18]。對于實際復雜形狀周圍的粘性流動，材料表面附近網格的質量在很大程度上影響流場的精度和效率[19-20]。本文使用多面體網格對模型進行網格劃分，先在表面生成面網格，在多孔圓盤附近做加密處理，最后轉化為體網格。其中，圖4為最終網格劃分情況，網格最大面尺寸0.000 05 m。

2 控制方程

本文求解使用的方法為有限體積法，有限體積離散的本質就是利用控制方程的積分形式，直接將其用于每一個曲邊格子，將空間的積分利用格林公式化為格子邊上的曲線積分，再利用格子的微元化，采用近似積分法，變為直接通量的加減[21-22]，如圖5所示。

圖4 網格劃分情況

計算流體力學的控制方程為連續性方程、動量方程和能量方程[23]，即

連續性方程

(1)

動量方程

(2)

(3)

能量方程

(4)

(5)

將三大方程在每個單元體上求解，再通過積分求得整個計算域的結果。

圖5 單位結構網格示意圖

3 邊界條件

來流入口選擇速度入口，出口為壓力出口，壓力設定為大氣壓，流體為空氣，密度和粘度設定為空氣的密度和粘度，各個壁面采用速度無滑移絕熱壁面。

在算法選擇上，Fluent默認提供了多種算法。分別是SIMPLE、SIMPLEC和PISO。這3種算法之間略有區別，其中SIMPLEC算法、PISO算法是以SIMPLE算法為基礎的，SIMPLE算法僅包含兩步，即先預測再修正。SIMPLEC算法與SIMPLE算法大致相同，只不過修改了部分壓力修正項中的系數，通過該修正，迭代的收斂速度大大提高[24]。PISO算法的前兩步與SIMPLE算法是一致的，在此基礎上，PISO算法增加了一側修正步驟。3種算法均有其獨特的適用條件，如在穩態條件下，SIMPLE算法和SIMPLEC算法效果更好，而在瞬態條件下，PISO算法效果最佳。考慮到本次研究忽略了時間因素，且該種模型相對簡單，所以選擇使用SIMPLEC算法，并且將殘差精度調小1e-04，得到精度相對更高的解。

4 結果分析

使用以上的邊界條件和網格，在速度入口處分別給出0.5、1、1.5、 2、2.5、3、3.5、4、4.5、5 m/s的速度，在Fluent中進行計算，通過收斂曲線圖6可以看出殘差已經降到1e-04以下，升力與升力系數值收斂，可以認為計算收斂。

圖6 收斂曲線

4.1 速度流線圖分析

在不同速度情況下氣流經過圓盤的流動情況如圖7所示，可以看出當風速小于1.5 m/s時，氣流流過圓盤不會產生渦流。當風速大于1.5 m/s,氣流流過圓盤會在圓盤上方出現一個分離于圓盤的、對稱的循環渦流，并且隨著風速增大，渦流的尺寸也隨之增大。故可以得到結論，在垂直于圓盤方向的風速大于1.5 m/s時，會在圓盤上方產生一個分離渦流，因此后文的分析忽略0.5、1、1.5 m/s的3個模型。

截取模型中某根細柱在長度由圓盤中心向外30%、50%、70%處的3個位置，其橫截面如圖8所示，分別在3個截面上作速度矢量圖，如圖9所示。可以看出氣流在流經細柱時呈繞流作用，外圍速度較大，表面速度較小，展示了細柱繞流的微觀流動。

圖8 某根細柱30%、50%、70%處截面

4.2 壓力分析

截取風速為1、2.5、3.5、4.5 m/s 4種典型情況下的圓盤周圍的壓力云圖，如圖10所示，可以看出在風速為1 m/s，沒有產生渦流的情況下，圓盤上方均為正壓區，上下表面的壓差僅來自于氣流在下表面速度損失所產生的正壓，壓差值較小；在風速為2.5、3.5、4.5 m/s時，圓盤上方的渦流在圓盤上方產生了一個負壓區，且速度越大，負壓區越大，中心區域負壓值越大，圓盤的上下表面壓差由下方正壓區和上方負壓區的差得到，因此壓差值較大。

圖9 3個截面上速度矢量圖

圖10 不同風速的截面壓力云圖

續圖10

圖11為風速2 m/s后渦環中心壓力(負壓)隨著速度變化的曲線圖，可以看出，隨著風速的增大，圓盤上方渦環中心的負壓隨之增大，且速度較大時，壓力的增加梯度比速度小時更大。

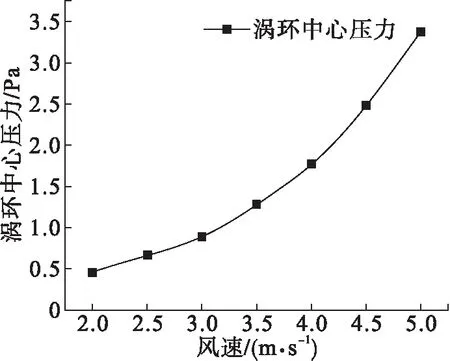
圖11 蒲公英種子模型渦環中心壓力(負壓)隨風速變化曲線圖

4.3 速度變化分析

如圖12所示，在渦環對稱中心沿X軸方向平行于圓盤作線段1，沿Y軸方向通過圓盤中心作線段2。

在不同風速下沿著線段1 作X方向速度變化曲線，結果如圖13所示。從圖13可以看出，所有的曲線都是速度先減小到接近于零，來流速度越大，減小越快，速度的最低點即是渦環中心，速度較小時，2個渦環中心的距離小。隨后氣流在2個渦環中心之間的速度又有所回升，在這之間，渦流的對稱中心即圓盤的正上方速度最高，來流速度越大時，回升越明顯。隨后速度呈對稱性，再次減小，之后回升到外界速度。

圖12 線段示例

圖13 蒲公英種子模型X方向速度分布匯總

在不同風速下沿著線段2作Y方向速度變化曲線，如圖14所示，氣流在圓盤下方速度快速減小，但在圓盤表面速度并沒有減小到零，隨后在圓盤上方速度繼續減小到最小值后開始回升，可以得到渦流是與圓盤分離的結論。

4.4 風速變化對升力特性的影響

升力隨速度變化的曲線如圖15所示，可以看到升力隨速度增加而增大，且升力隨速度變化的曲線的斜率逐漸變大，所以圓盤上方的分離渦流會使圓盤的升力變大。

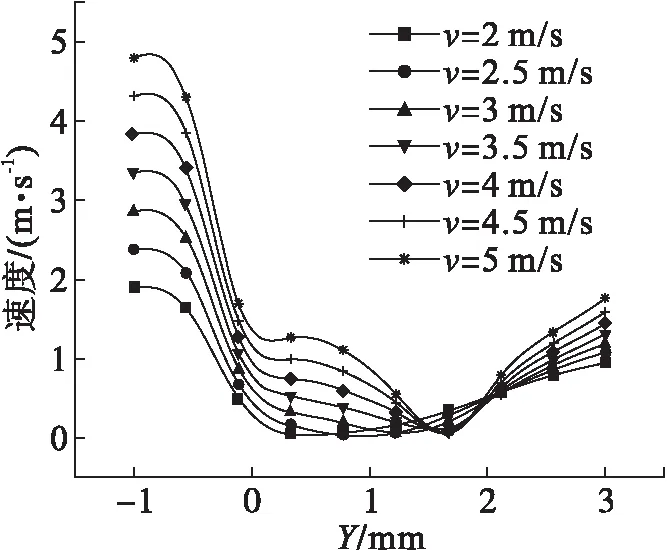
圖14 蒲公英種子模型Y方向速度分布匯總

圖15 蒲公英種子模型升力隨風速變化曲線圖

本文探討低速不可壓流動，升力產生的原因是上下表面的壓差值。圖16展示了v=1 m/s和v=3 m/s時圓盤上下截面上的速度矢量。在v=1 m/s時所有的速度方向都是向上的，v=3 m/s時渦環內出現大量方向向下的速度矢量，圖17為v=1 m/s和v=3 m/s時截面壓力云圖，可以看出速度越大時，下表面的正壓值越大，上下表面的壓差值越大，即圓盤升力越大，且v=5 m/s時，這些渦環內向下的速度使圓盤上方產生了一個帽型負壓區，使圓盤上下表面的壓差大于下表面的正壓值，所以會使升力-速度變化曲線斜率逐漸變大。

升力系數為一個無量綱值，公式為

(6)

(7)

升力系數隨著速度變化的曲線如圖18所示，在風速增大時，升力系數減小，曲線斜率逐漸減小。

圖16 不同風速時截面速度矢量圖

圖17 不同風速時截面壓力云圖

圖18 蒲公英種子模型升力系數隨風速變化曲線圖

5 結論

本文通過三維建模軟件CATIA建立了蒲公英種子的簡化多孔圓盤模型，對模型及外流場劃分非結構化網格。在CFD軟件中，從風速為零開始以0.5 m/s的增加幅度依次進行數值計算，最終發現在風速大于1.5 m/s時，在圓盤上方出現分離渦環；當風速小于1.5 m/s時，氣流流經圓盤后的速度與在圓盤外流過的氣流速度差不足以形成渦流。

由速度變化曲線可以看出渦環中心的速度最小，渦環的速度變化在水平方向呈對稱性，垂直方向速度變化曲線可以看出渦環是分離于圓盤的。

由壓力云圖和渦環中心可以得到在圓盤上方沒有產生渦流時，圓盤上方均為正壓區，上下表面的壓差僅來自于下表面的正壓，壓差值較小；在風速大于 1.5 m/s時，圓盤上方產生分離的渦流，它使圓盤上方產生了一個負壓區，且速度越大，負壓區越大，中心區域負壓值越大，圓盤的上下表面壓差由下方正壓區和上方負壓區的差得到，因此壓差值較大，升力較大。