非對稱錐優(yōu)化問題KKT函數(shù)的B次微分非奇異性與非退化性條件

趙金陽,王詩云

(沈陽航空航天大學(xué) 理學(xué)院，沈陽 110136)

考慮下面的一類非對稱錐

K={(s,s0)∈Rn×R:eTs≤ks0,0≤s≤s0e}

其中k>0,e表示所有元素為1的向量。在以前的工作中，已經(jīng)得到了K上投影算子的閉形式[1]、變分幾何性質(zhì)[2]以及投影算子的B次微分[3]。本文考慮如下的優(yōu)化問題:

minf(x)

G(x)∈K.

(1)

其中函數(shù)f:Rm→R和G:Rm→Rn×R是二次連續(xù)可微的。為了方便起見，令

K=:={(s,s0)∈Rn×R:eTs=ks0,0≤s≤s0e}.

本文研究KKT函數(shù)的強二階充分條件、約束非退化性、B次微分非奇點與KKT點強正則性之間的關(guān)系。

K上的投影算子有著廣泛的應(yīng)用，可以參考。其中Liu等[1]得到了該投影算子的閉形式。本文用∏K(·,·)來表示K上的投影算子。

最優(yōu)解的靈敏度和穩(wěn)定性分析是優(yōu)化問題中最重要的研究領(lǐng)域之一，它與最優(yōu)條件和增廣拉格朗日方法有著密切的聯(lián)系。對于多面體的情況，許多學(xué)者取得了優(yōu)秀的研究成果，例如， Rockafellar[11]，Kojima[12]，Robinson[13]，latte等[14]，Bonnans等[15]。然而，這些成果并沒有建立起最優(yōu)解與KKT系統(tǒng)之間的聯(lián)系。Sun[16]和Chan[17]在研究非線性半正定的規(guī)劃問題時，研究了KKT函數(shù)的強二階充分條件、約束不變性、B次微分非奇異性與KKT點強正則性之間的關(guān)系。此后出現(xiàn)了許多類似的結(jié)果:二階錐的線性規(guī)劃情形可參考文獻(xiàn)[18]；一般對稱錐的線性規(guī)劃情形可參考文獻(xiàn)[21]；非對稱錐的線性規(guī)劃情形可參考文獻(xiàn)[22]。

基于在K上的投影算子的廣泛應(yīng)用以及靈敏度分析在優(yōu)化問題中的重要性，本文側(cè)重建立最優(yōu)化問題(1)的強二階充分條件、約束不變性、KKT函數(shù)的B次微分非奇異性和局部最優(yōu)解的強正則性的聯(lián)系。

1 符號說明和預(yù)備知識

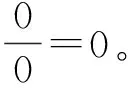
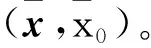
B={z∈Rn:0≤z≤e,eTz≤k},

(2)

α:={i∈[1:n]:xi≤σ},

β:=[1:n](α∪β)

(3)

(4)

其中σ是(x,x0)的參數(shù)，它的值可參照文獻(xiàn)1中，命題2.2和算法3.1。

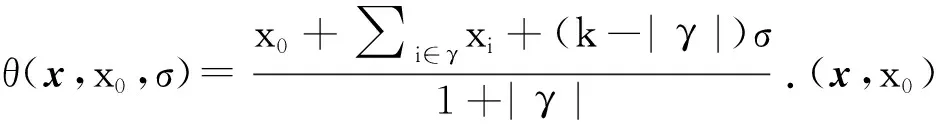
(5)

其中i∈[1:n],

(6)

定理2[2]集合K的對偶錐和極錐可分別計算為

(7)

設(shè)π是在[1:n]上的一對一映射，而且xπ(i)≤xπ(i+1)，i∈[1:n-1].令

I=(x)={i∈[1:n]:xi=(xπ(?k」+1))-},

J=(x)={i∈[1:n]:xi=(xπ(n-?k」))+},

I<(x)={i∈[1:n]:xi<(xπ(?k」+1))-},

J<(x)={i∈[1:n]:xi<(xπ(n-?k」))+},

I>(x)={i∈[1:n]:xi>(xπ(?k」+1))-},

J>(x)={i∈[1:n]:xi>(xπ(n-?k」))+}.

則

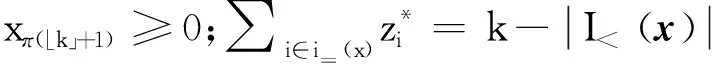
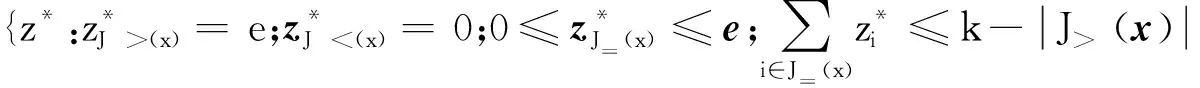
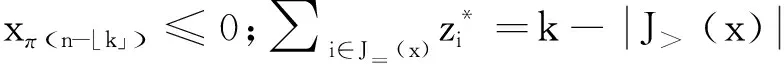
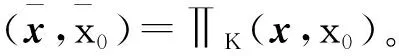
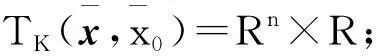
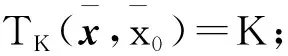
(c)否則

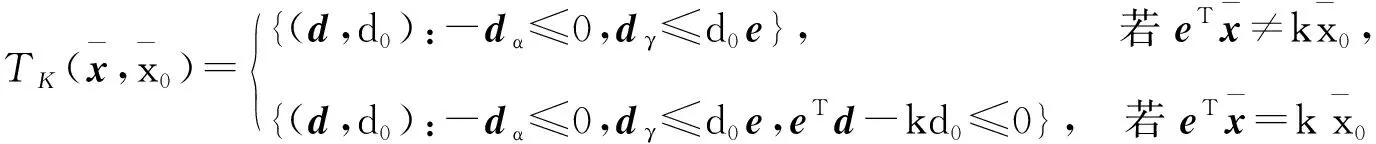
(8)

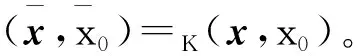
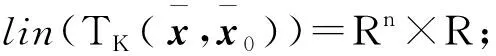
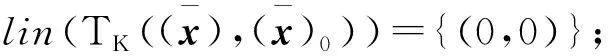
(c)否則

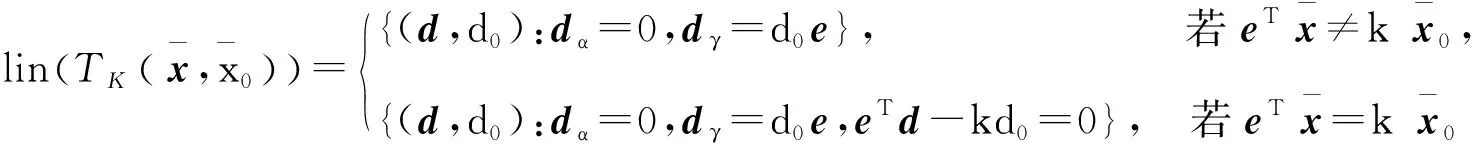
(9)

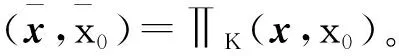
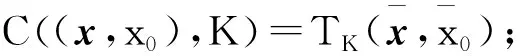
(b)如果(x,x0)∈bd(Ko){(0,0)},則max{xTz:z∈B}+x0=0且

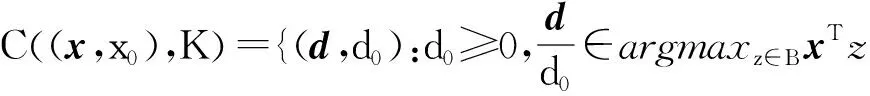
∑i∈J=(x)di≤(k-|J>(x)|)d0當(dāng)xπ(n-k)≤0;

(10)

∑i∈J=(x)di=(k-|J>(x)|)d0當(dāng)xπ(n-k)>0}.

(c)如果(x,x0)∈int(Ko),則C((x,x0),K)={(0,0)};

(d)否則，C((x,x0),K)計算如下

C((x,x0),K)=

(11)

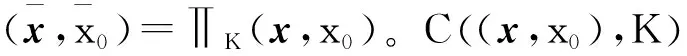
(a)如果(x,x0)∈K,則aff(C((x,x0),K))=Rn×R;

(b)如果(x,x0)∈bd(Ko){(0,0)},則aff(C((x,x0),K))為

(i)當(dāng)xπ(n-k)≤0,

aff(C((x,x0),K))=

{(d,d0)∈Rn×R:dJ>(x)=d0e;dJ<(x)=0};

(ii)當(dāng)xπ(n-k)>0,

aff(C((x,x0),K))=

{(d,d0)∈Rn×R:dJ>(x)=d0e;dJ<(x)=0;

(c)如果(x,x0)∈int(Ko),則aff(C((x,x0),K))={(0,0)};

(d)否則，

aff(C((x,x0),K))=

(12)

2 問題(1)的臨界錐

這一節(jié)，考慮問題(1)的KKT點。令x∈Rm是問題(1)的可行點，則拉格朗日函數(shù)為

L(x,Λ)=f(x)-〈G(x),Λ〉

(13)

其中Λ∈Rn×R是拉格朗日乘子，為討論方便，G(x)記為

G(x)=(g(x),g0(x)),g(x)=(g1(x),…,gn(x))T,

并且Λ記為

Λ=(λ,λ0),λ=(λ1,…,λn)T.

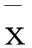
(14)

則

K*

(15)

及

(16)

考慮式(16)，根據(jù)定理1，可得：

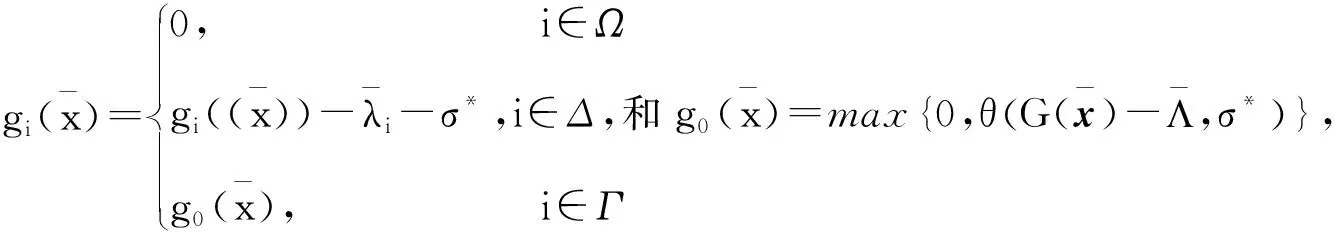
(17)

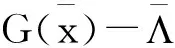
結(jié)合式(17)和式(18)，Ω、Δ和Γ可記為

與α≠,α=,γ≠,γ=的定義與式(4)類似，我們定義Ω≠,Ω=,Γ≠和Γ=:

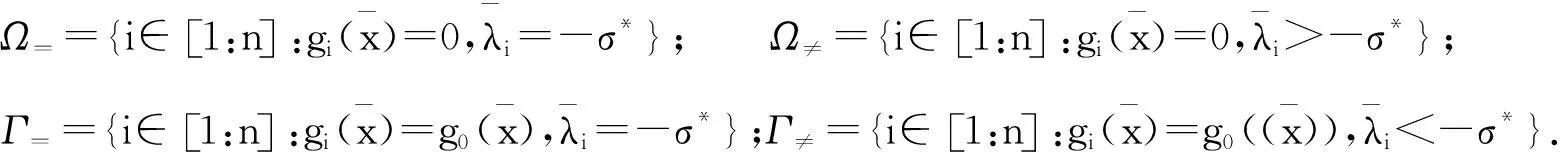
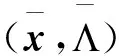
(20)

根據(jù)式(14)有

這意味著

相比式(20)，只需要證明這一點

(21)

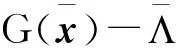
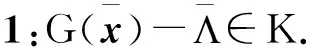
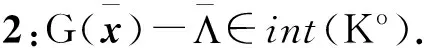
(22)

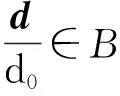
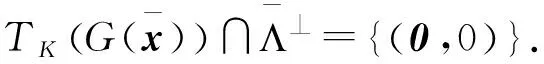
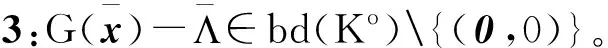
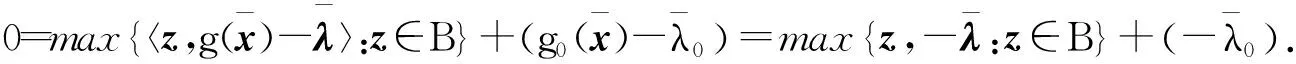
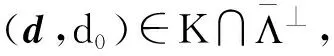
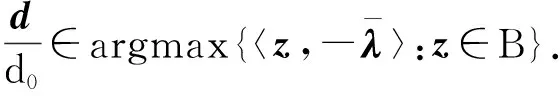
當(dāng)d0>0

}.

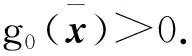
這意味著

(23)

和

(24)

根據(jù)式(23)有:

和

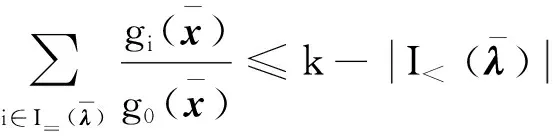
(25)

(26)

和

(27)

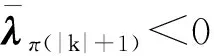
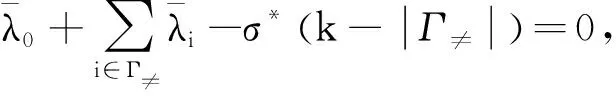
(28)

和

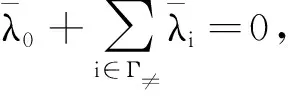
(29)

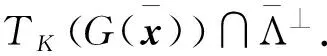
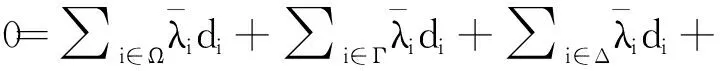
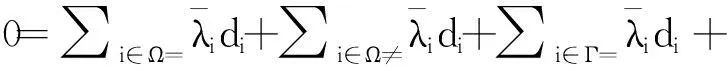
通過式(27)和式(28)有

≥-σ*(∑i∈Ω≠di+∑i∈Γ≠(di-d0))+∑i∈Ω=di+∑i∈Γ=di+∑i∈Δdi-(k-|Γ≠|(zhì))d0)

=-σ*(eTd-|Γ≠|(zhì))d0-(k-|Γ≠|(zhì))d0)

=-σ*(eTd-kd0)

=σ*(kd0-eTd)

≥0,

這表明

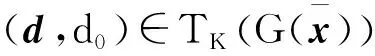
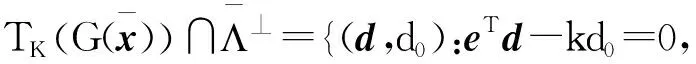
dΓ≠=d0e,dΩ≠=0,dΩ=≥0,dΩ=≤d0e}.

3 強二階條件,非退化性約束和B次微分的非奇異性

本節(jié)討論問題(1)的二階條件，約束非退化性條件和KKT函數(shù)的B次微分的非奇異性。為此定義

(30)

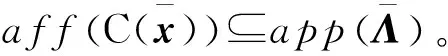
(31)

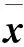
(32)

考慮定理4、定理5和式(21)，非退化約束強于嚴(yán)格約束規(guī)范。

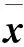
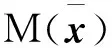
(33)

(34)

如果t足夠大，再次運用定理5和式(20)有

(35)

因為K是多面體，Sigma項等于0，因此問題(1)的二階條件可以刻畫為如下定理。

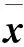
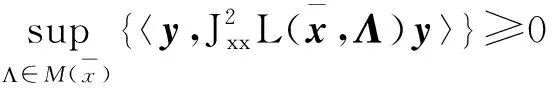
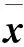
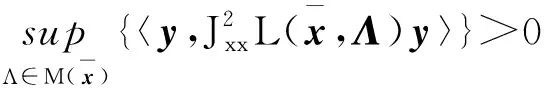
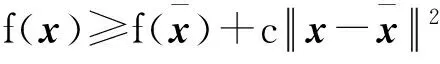
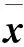
(36)

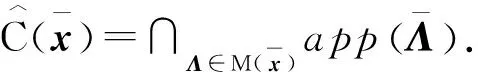
接下來將討論B次微分非奇異性與約束非退化性之間的關(guān)系。定義KKT函數(shù)為

然后，這種情況(14)等價于

(37)

或者等價于下面的廣義方程

(38)

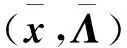
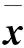
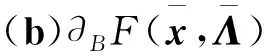
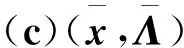
有(a)?(b)?(c)成立

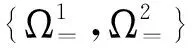
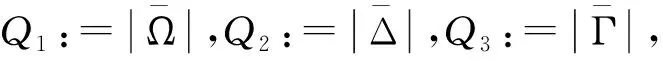
PΔΩΓ表明一個排列有

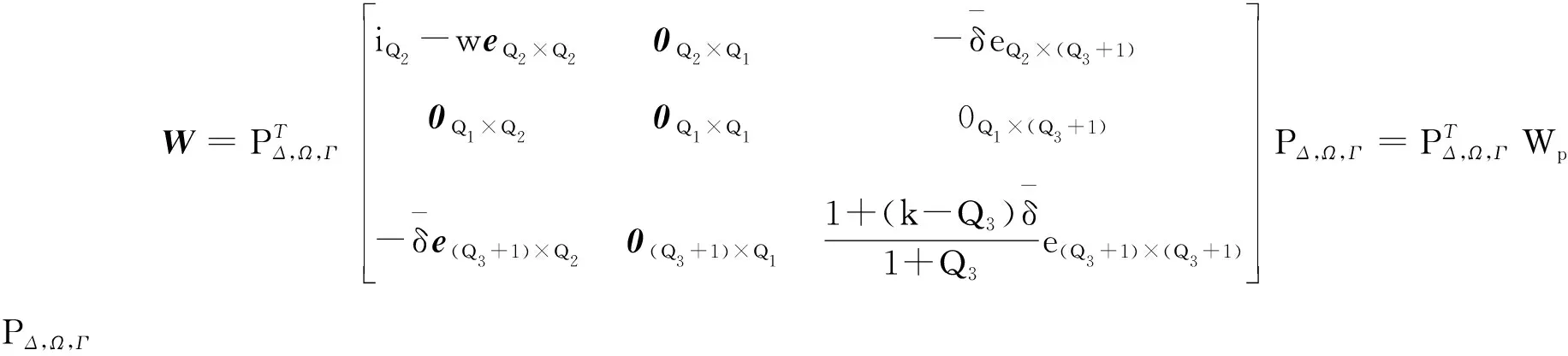
(39)

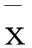
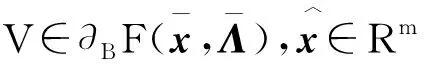
(40)

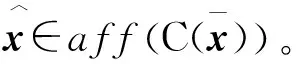
(41)

(42)

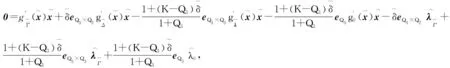
(43)

(44)

根據(jù)式(42)有

(45)

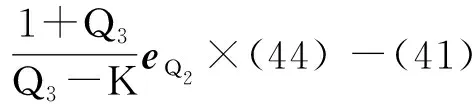
(46)

令eQ3×(44) -(43)，有

(47)

這意味著

(48)

現(xiàn)在，把式(46)和式(48)代入式(44)有

(49)

結(jié)合式(42)和式(48)，有

(50)

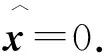
根據(jù)式(40)中第一個和第二個等式，結(jié)合W的對稱性有W,I-W為投影的廣義雅可比矩陣，且

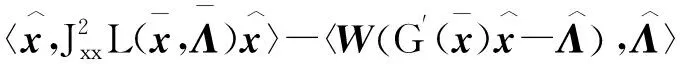
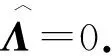
(51)

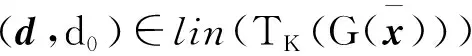
(52)

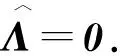
“(b)?(c)”.同理[16, 命題3.2].

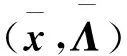
(53)

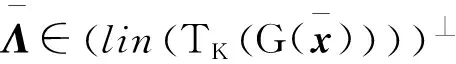
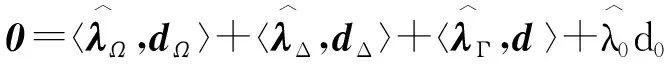
(54)

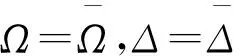
(55)

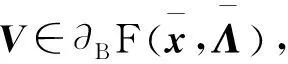
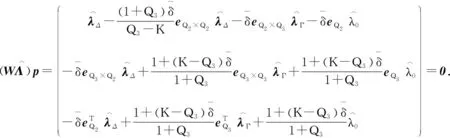
(56)

4 結(jié)論

本文給出了KKT系統(tǒng)的強二階充分條件、非退化約束性、B次微分非奇性與KKT點的強正則性之間的聯(lián)系。在以后的工作中將研究增廣拉格朗日方法。