基于預處理共軛梯度迭代法的電力系統狀態估計算法

李建斌，王鵬程，傅 侃，方 睿，董樹鋒

（1. 國網浙江杭州市蕭山區供電有限公司，浙江省杭州市 311200；2. 杭州電力設備制造有限公司蕭山欣美成套電氣制造分公司，浙江省杭州市 311200；3. 浙江大學電氣工程學院，浙江省杭州市 310027）

0 引言

電力系統狀態估計是現代能量管理系統（energy management system，EMS）的基礎，為EMS中的高級應用提供底層支撐。隨著中國電力系統省地一體化［1］和輸配一體化［2］的發展，電力系統計算維度越來越高，計算時間急劇增加，傳統狀態估計算法難以滿足快速增長的計算需求。因此，亟須研究更加快速準確的電力系統狀態估計算法。

目前，電力系統中最廣泛使用的狀態估計算法是加權最小二乘（weighted least squares，WLS）法［3］。這種方法假設量測量服從正態分布，數學模型較為簡單、迭代次數少、計算速度快，在測點集中、無不良數據時估計效果較好。WLS 狀態估計方法以牛頓-拉夫遜法為基礎，通過逐次線性化、多次求解線性方程組的方式，反復迭代得到狀態變量的最終解。在WLS 狀態估計方法的求解過程中，需要耗費大量的時間求解高維稀疏矩陣乘法和高維稀疏線性方程組，占據了絕大部分的計算時間。同時，由于WLS 狀態估計方法抗差性較差，有學者也提出了一些抗差狀態估計方法［4-5］，能夠減少不良數據對狀態估計結果的影響。

求解大規模稀疏線性方程組主要可以分為直接法和迭代法。直接法是利用矩陣分解和變換技術對原線性方程組進行消去，代表方法有高斯消去法［6］、LU 分解法［7］等。這類方法的特點是對主元的選取較為苛刻，對于病態的稀疏矩陣需要通過置換行列的方式得到合適的對角主元。同時，直接法占用的內存較多，難以并行計算，在方程規模達到一定數量級后求解效率較低，不適合計算大型稀疏線性方程組。文獻［8-10］使用直接法求解電力系統潮流和狀態估計問題；文獻［11-12］通過圖形處理器（graphics processing unit，GPU）對狀態估計算法進行并行加速，在稀疏線性方程組求解方面采用并行LU 分解算法，但并行的LU 分解法加速效果不明顯，不適合運用在大規模系統中。

相比于直接法，迭代法對于大型稀疏線性方程組的計算具有較大的優勢。迭代法每次計算時的內存占用低，且非常適合并行，當矩陣規模增大時迭代法的計算效率不會受到影響。但其主要問題在于收斂性，受矩陣的條件數影響較大。目前，針對這一問題，主要采用預處理技術降低條件數，代表方法有不完全LU 分解法［13］、不完全Cholesky 分解法等［14］。近年來，由于電力系統規模的不斷增大，已有不少研究將迭代法運用在電力系統分析和計算領域。文獻［15-17］對潮流計算中的雅可比矩陣進行預處理，并利用迭代法并行計算線性方程組，解決了大規模潮流計算的效率問題。文獻［18］提出了一種基于不完全LU 分解預處理迭代法的潮流計算法，但該方法主要針對的是潮流計算問題而沒有能夠擴展到狀態估計問題。

本文基于預處理共軛梯度迭代法，針對WLS 狀態估計的特點，提出一種快速的電力系統狀態估計算法。該算法在預處理后矩陣條件數得到明顯下降，同時基于GPU 并行計算技術實現矩陣乘法和迭代法的高效并行。算例分析驗證了本文算法的快速性、收斂性和低內存占用等特點。

1 狀態估計基本原理

1.1 WLS 狀態估計

電力系統的非線性量測狀態估計方程可以表示為：

式中：z為系統量測向量；x為系統狀態變量；h（x）為在狀態x下的量測函數；v為量測誤差。

定義殘差矢量為：

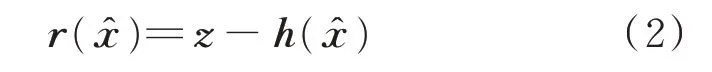
求解狀態估計問題變為求解潮流問題的擴展，可以建立優化模型：

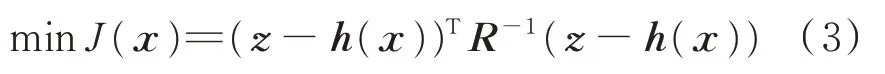
式中：R為量測誤差方差矩陣，表示各量測量的準確程度。

為了使式（3）的目標函數值最小，則有：

采用牛頓法求解，可以得到迭代修正量［19］為：

1.2 并行性分析

GPU 的統一計算設備架構（compute unified device architecture，CUDA）［20］具備并行計算功能，非常適合處理矩陣和向量的并行運算。

從式（5）可以看出，WLS 狀態估計中耗時部分主要是矩陣乘法與線性方程組求解這2 個步驟。在牛頓法的每一次迭代過程中都需要求解矩陣乘法和線性方程組，其中涉及大量運算，占據了耗時的絕大部分。

矩陣乘法步驟包括矩陣A和向量b的運算，其計算公式如下。

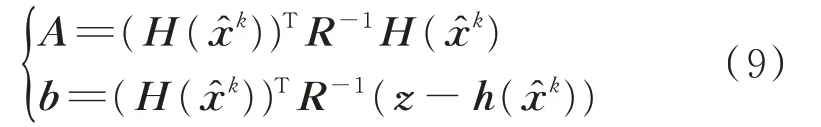
由于矩陣H(x?k)為高維稀疏矩陣，因此經過矩陣乘法后矩陣A仍是高維稀疏矩陣。在向量b中，由于向量z?h(x?k)為稠密向量，因此b也是高維稠密向量。 此步驟采用CUDA 中的運算庫cuSPARSE［21］即可并行高效計算出矩陣A和向量b的結果，根據CUDA 的描述，計算速度比純CPU 替代產品快2 至5 倍。

矩陣線性方程組計算部分最為耗時。從式（9）可以看出，矩陣A是矩陣轉置、誤差權重矩陣和矩陣本身之間的乘積，是對稱正定矩陣。當系統規模較小時，矩陣規模較小，適合使用LU 分解等直接法對線性方程組進行計算。常用的高性能線性方程組求解庫SuperLU［22］經過了高度優化，屬于直接法，效率較高。但對于大規模稀疏線性方程組，矩陣條件數較高，直接法的計算效率難以滿足要求，適合在GPU 上使用迭代法進行并行計算。

2 迭代法基本原理

2.1 Krylov 子空間法

Krylov 子空間法是求解大規模線性方程組的首選方法。求解一般線性方程組：

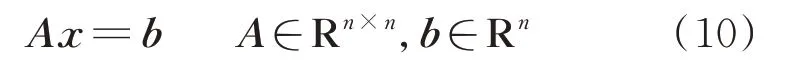
投影方法的基本思想是從一個維數更小的子空間Km內尋找近似的解。這個子空間Km被稱為搜索空間，其維度為m。

此時，設置m個約束，要求殘差矢量r滿足m個正交條件，即Petrov-Galerkin 條件：

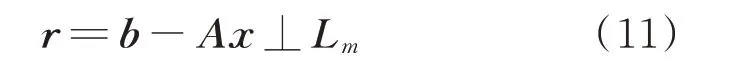
式中：Lm為另一個m維的子空間，被稱為約束空間。當Lm=Km時，該方法為正交投影法，否則為斜投影法。

給定迭代初值x0，采用仿射空間x0+Km可以得到：

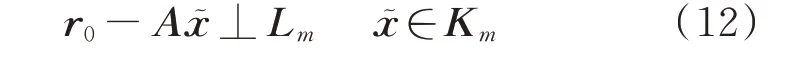
式中：x?為迭代值，初始殘差r0=b?Ax0。

在Krylov 子空間方法中，搜索空間Km就是Krylov 子空間，定義為：

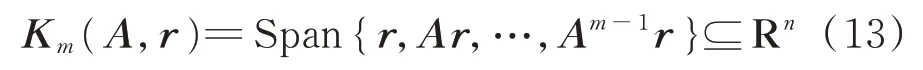
式中：r可選為初始殘差r0，Krylov 子空間方法就是在Krylov 子空間中尋找近似解。

當選用不同的約束空間Lm時，對于迭代過程會有比較大的影響。主要可以分為如下方法。

1）正交投影法：Lm=Km(A，r0)，代表方法有共軛梯度法。該方法計算步驟較為簡單，但要求矩陣A對稱正定。

2）正交化方法：Lm=AKm(A，r0)，代表方法有廣義極小殘差方法。該方法數值穩定性高，但計算量會隨迭代的步數線性增長。

3）雙正交化方法：Lm=AKm(AT，r0)，代表方法有穩定的雙正交共軛梯度法。該方法適用性最廣且穩定性較高，但計算步驟較為復雜，計算量比前2 種方法要大。

搜索空間Km的選取不會對最終狀態估計結果的精度有影響，其選取依據主要是狀態估計中矩陣A的特性，例如是否對稱、是否正定等。在狀態估計的系數矩陣A對稱正定情況下，可以使用正交投影法確定約束空間Lm，此方法計算量較小、步驟較簡單。本文采用共軛梯度法進行求解。從式（9）可以看出，矩陣A為對稱正定矩陣，滿足共軛梯度法的要求，能夠充分發揮其計算步驟簡單、效率高的優勢。

2.2 預處理方法

如果直接使用上述Krylov 子空間方法進行迭代，原始矩陣條件數過高，可能會出現收斂性差、迭代次數多等問題。采用合適的預處理方法可以降低矩陣條件數。預處理方法的原理是通過預處理子M將原始線性方程組轉化為另一個易于求解的線性方程組。

常見的預處理方法可分為如下幾類［23］。

1）左預處理：對M?1Ax=M?1b使用迭代法。

2）右預處理：對AM?1u=b使用迭代法，其中x=M?1u。

3）分裂預處理：對M1?1u=M1?1b使用迭代法，預處理子M=M1M2。

對于大規模電力系統，其矩陣條件數較高，利用預處理技術可以減少迭代次數，易于問題求解。不完全LU 分解預處理方法適用范圍廣，且在文獻［18］中已經被證明在潮流計算中有較好的預處理效果。因此，本文選用不完全LU 預處理方法。

2.3 預處理共軛梯度迭代法

考慮對稱正定矩陣A，并假設有一個預處理子M可供使用，且M是對稱正定的。為了保持對稱性，注意到M?1A對M內積(x，y)M≡(Mx，y)=(x，My)是自伴的，因為

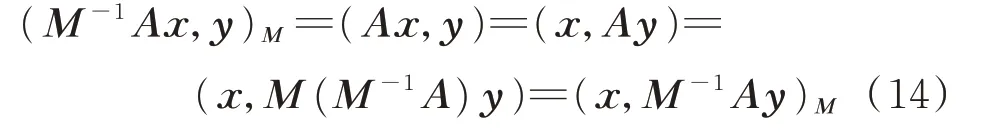
式中：x和y為任意向量。

所以，一種選擇是用M內積代替共軛梯度迭代法中的歐氏內積，如果按這種新內積重寫共軛梯度迭代法，用rj=b?Axj表示原殘差，而用zj=M?1rj表示預處理方程組的殘差，可以得到本文所使用的預處理共軛梯度迭代法，且不需要顯式地計算M內積。預處理共軛梯度迭代法的具體步驟見3.1 節。

3 GPU 并行加速狀態估計算法

3.1 算法步驟

本文提出一種基于預處理共軛梯度迭代法的電力系統WLS 狀態估計算法，其計算步驟如下。

步驟1：初始化，形成節點導納矩陣，給狀態變量賦初值形成x?0。

步驟2：設置迭代變量k=0 和最大迭代次數kmax。

步驟3：根據當前狀態變量，計算雅可比矩陣H()，計算公式如文獻［19］附錄中所示。

步驟4：在GPU 上利用cuSparse 庫，根據式（9）計算矩陣A和向量b。

步驟5：在GPU 上求解線性方程組Ax=b，利用矩陣A對稱正定的特點，使用預處理共軛梯度法進行迭代求解［24］，具體做法如下。

①對矩陣A進行ILU（0）分解，ILU（0）分解是不完全LU 分解的一種形式，形成矩陣A的預處理子：

式中：L和U分別為ILU（0）分解出的上三角矩陣和下三角矩陣。設置迭代次數i=0 和最大迭代次數imax，設x的初始猜測為x0，計算初始殘差r0及其2 范數‖r0‖。

②根據L和U求解方程組Mz=ri，其中ri為迭代次數為i時的殘差，得到z后計算ρi=(ri，z)。

③如果i=0，則令pi=z，否則令β=ρi/ρi?1，并計算pi=z+βpi?1。

步驟6：根據步驟5 中解出的x即可得到牛頓法迭代的修正量Δx?k，根據式（7）得到狀態變量x?k+1。

步驟7：令k=k+1，若不滿足式（8）且k沒有達到kmax則轉至步驟3，否則退出狀態估計過程。

3.2 算法特點

1）算法采用ILU（0）預處理方法，保證了殘差矩陣滿足ILU（0）的分解條件。這種預處理方法產生的預處理子不會注入非零元。經過預處理后，能夠保證預處理子的稀疏性。在大型稀疏矩陣中，保證預處理子的稀疏性可以在矩陣運算中節省計算量和內存，同時利用預處理子與原矩陣相同的稀疏性能夠更快地加速迭代法的計算。從迭代步驟可以看出，計算只涉及稀疏矩陣向量線性乘法，且由于沒有更多的非零元注入，理論上不會產生內存泄漏。

2）算法采用了共軛梯度法，WLS 狀態估計中線性方程組系數矩陣A對稱正定的特性使共軛梯度法苛刻的適用條件得到滿足。在大型稀疏線性方程組求解過程中，迭代法的計算效率更高，同時共軛梯度法作為迭代法中計算步驟最簡單的方法，具有最少的計算量和最高的計算效率。

3）算法采用了GPU 并行計算架構，充分利用CUDA 的高性能矩陣向量計算技術和cuSparse 庫的乘法運算，加速矩陣A和向量b的形成。同時，在共軛梯度法迭代過程中，使用GPU 快速計算各個中間變量，保證了迭代法的快速計算。

4 算例分析

為了分析本文所提算法的有效性，選取部分算例進行測試。其中，CASE300 是IEEE 標準測試算例，分別將10、20、50、100 個CASE300 算例以平衡節點為中心進行拼接，可以得到拼接算例CASE2991、 CASE5981、 CASE14951和CASE29901。本文的量測數據是在潮流計算的基礎上加入2%的高斯噪聲所形成的。算例測試環境為64 bit 的Windows 10 操作系統，CPU 型號為Intel Core i7-5820K，GPU 型號為NVIDIA GeForce GTX1080。其中，牛頓法的迭代精度設置為10?3，線性方程組求解的迭代精度設置為10?10。

4.1 計算耗時對比

為了分析本文算法的并行加速效果，將本文算法與直接法進行比較。其中，直接法使用高性能SuperLU 庫，能夠較快地使用列選主元高斯消去法求解高性能稀疏線性方程組，計算結果如表1所示。

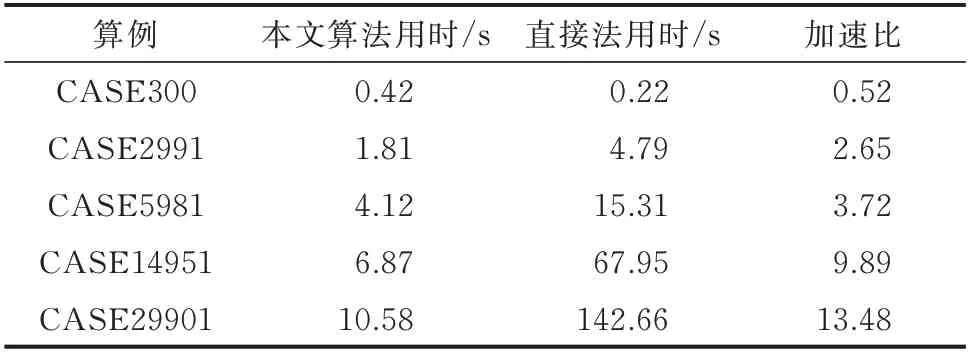
表1 本文算法與直接法計算效果對比Table 1 Comparison of calculation results between method of this paper and direct method

從表1 可以看出，本文算法隨著算例規模的增大，計算加速效果越來越明顯。當算例規模較小時，如CASE300 算例中本文算法計算速度比直接法更慢，這是由于直接法在線性方程組維數較小時LU分解速度較快。但當系統規模增大時，本文算法受問題規模的影響較小，而此時直接法的計算時間會急劇增大。上述算例證明在大規模電力系統中，本文算法能夠大幅提高計算速度，與直接法相比優勢明顯。

4.2 計算精度對比

為了分析本文算法的估計精度誤差，將本文算法與直接法進行比較。通過計算本文算法和直接法估計結果與真值之間的平均相對誤差來評估計算精度，計算結果如表2 所示。

表2 本文算法與直接法計算精度對比Table 1 Comparison of calculation precision between method of this paper and direct method

從表2 可以看出，使用本文算法狀態估計結果的平均相對誤差在2%以內，與直接法精度相比幾乎沒有差別。從計算步驟上來看，本文方法與直接法的不同之處在于求解線性方程的步驟，而由于線性方程組的迭代精度設置較為嚴苛，設為10?10，求得方程的解與直接法相差無幾。算例結果表明本文算法不會對狀態估計精度造成過大的影響。

4.3 預處理技術有效性分析

良好的預處理有助于減少迭代次數，改善迭代法的穩定性。為了驗證本文所采用的ILU（0）預處理方法的有效性，對預處理前后矩陣的條件數和迭代次數進行分析，計算結果如表3 所示。其中，預處理條件數和迭代次數取各次迭代的平均值。

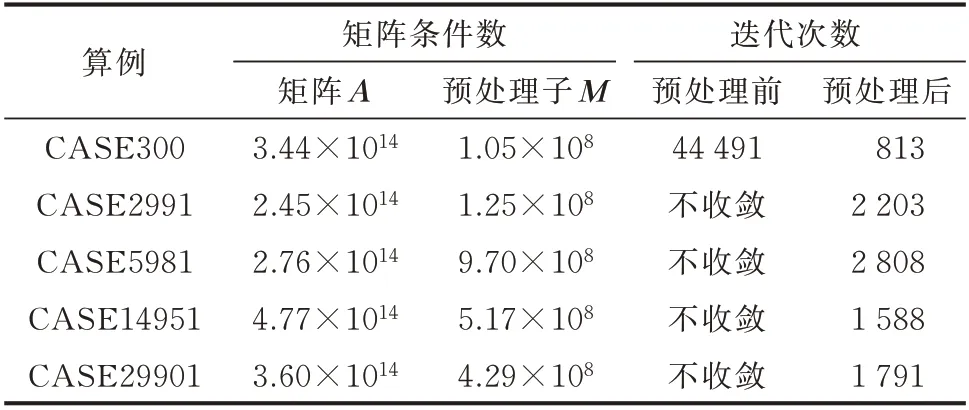
表3 ILU(0)預處理方法效果分析Table 3 Effect analysis of ILU(0)preprocessing method

從表3 可以看出，經過ILU（0）預處理后，預處理子的條件數大幅下降。在迭代法中，每次求解都需要計算預處理子所形成的線性方程組，條件數下降意味著更容易對該方程組進行求解。因此，預處理后共軛梯度法的迭代次數也隨之下降，甚至可以改善原本不收斂的線性方程組的收斂性。

減少迭代次數能夠縮短計算時間，且該預處理方法不注入非零元，不會因稀疏性被破壞而大幅增加計算時間。算例結果表明，本文所采用的預處理方法能夠有效減少共軛梯度法的迭代次數，提高本文算法的計算效率。

4.4 內存占用測試

在大型電力系統計算中，內存占用是一個重要的性能指標。為了驗證本文算法的內存占用情況，對內存占用和顯存占用進行測試，計算結果如表4所示。

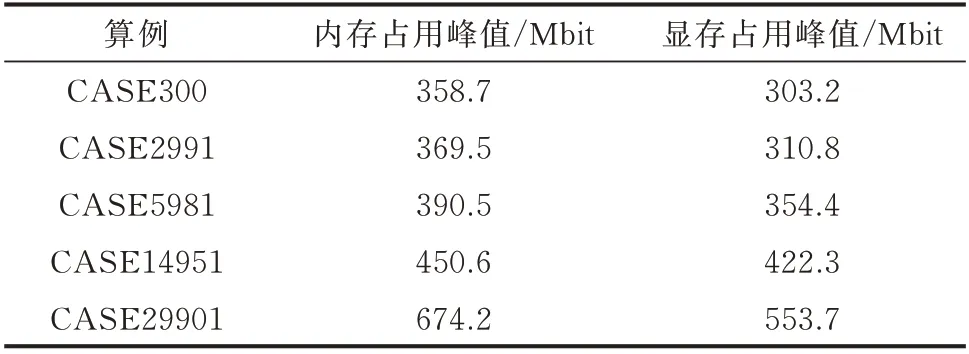
表4 本文算法內存占用測試Table 4 Memory footprint test of method in this paper

本文算法為了節約內存，矩陣存儲方式為壓縮矩陣形式。從表4 可以看出，即使對于節點數約3 萬的大規模電力系統，本文算法內存占用不超過700 Mbit，顯存占用不超過600 Mbit。整體而言，本文所用算法內存和顯存占用峰值都較低，在普通的計算機上即可進行計算。

5 結語

針對大型電力系統狀態估計速度較慢的問題，本文提出了一種基于預處理共軛梯度迭代法的電力系統狀態估計算法。本文算法是在WLS 狀態估計法的基礎上，針對牛頓法求解過程中矩陣乘法和大規模稀疏線性方程組求解效率較低的特點，在GPU上進行并行加速。由于WLS 狀態估計中線性方程組稀疏矩陣為對稱正定矩陣，滿足共軛梯度法的使用條件，本文提出采用不完全LU 分解預處理方法和共軛梯度迭代法進行線性方程組的求解。算例分析驗證了本文算法計算速度快、內存占用低的特點，并驗證了預處理方法的有效性。綜上所述，本文所提算法能夠滿足大規模電力系統狀態估計的實時性要求，未來可考慮多機多卡下的分布式計算，進一步提高狀態估計的計算效率。