不同圓角半徑對三通應力集中區域影響的量化分析

李海洋，郭延軍，王 魯，許 輝，酈曉慧

(華電電力科學研究院有限公司，杭州 310030)

0 引言

在火電廠管道系統中，三通是其中一種重要的構件[1]，其為管系載荷的集中部位，除受內壓作用外，還受到軸向力、扭矩、彎矩的作用[2]。三通相當于在主管上開孔，并接入支管。由于支管與主管相貫使結構不連續，導致在三通管線相貫線拐角處造成極大的應力集中，形成高應力區[3-5]。

三通管件本身的成本不高，但是因失效引起的停機和事故所帶來的經濟損失往往是巨大的[6]。目前，軒福貞等[7-8]研究學者通過有限元對三通管件進行應力分析表明，三通的應力集中區在肩、腹部位置，且改變圓角半徑能有效降低應力集中。承壓設備表現出高溫、高壓、大型化、重載等極端化趨勢，并隨著傳統應力分類方法的弊端日益突顯[9]，使得結構性能特征和承載潛力的安全性分析與設計受到學術界重視[10]。ALASWAD等[11]采用有限元和響應面法，對T型管成形過程進行多目標優化，將工藝參數作為設計變量，研究了設定的變量因素對厚度減小和脹起高度的影響；朱書建等[12]采用正交試驗方法并結合有限元仿真分析，對T型三通進行優化。

本次研究基于有限元分析軟件[13]，并用圖像方法將三通的應力分布狀態轉化為三維圖像，其中像素值的大小就是應力值大小；通過圖像處理方法對管件的應力集中區域進行提取，并從應力集中區域的體積大小、應力分布、局部最大等效應力、應力集中系數及應力集中區域的形狀等方面進行分析及安全評估。

1 有限元計算模型

1.1 三通尺寸

該三通是由熱壓法制造，主管和支管都比較短[14]。本文建立的三通計算模型如圖1所示，采用有限元軟件進行應力計算。因需對三通管件的肩部、腹部位置分別進行分析，取三通的1/2作為有限元計算的模型。

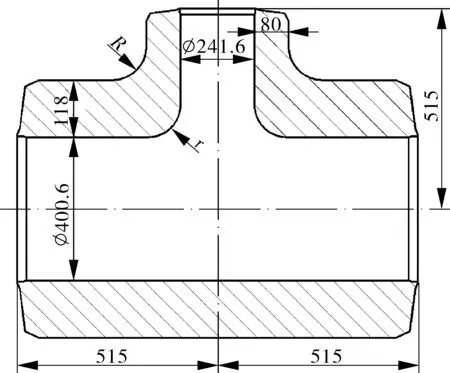
圖1 三通管件結構尺寸示意Fig.1 Schematic diagram of structural dimensionsof tee pipe fittings

圖1中，r與R分別代表三通管件的內圓角半徑與外圓角半徑。分析三通的肩部位置，其內圓角半徑分別為r=0，30，60，90，120，150，180 mm，外圓角半徑R=95 mm；分析三通管件的腹部位置，其外圓角半徑R=0，30，60，95，125，155，185 mm，內圓角半徑r=90 mm。

1.2 位移、約束及加載

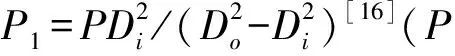
(a)肩部位置加載

(b)腹部位置加載圖2 三通管件加載示意Fig.2 Loading diagram of tee pipe fitting

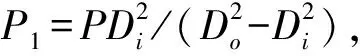
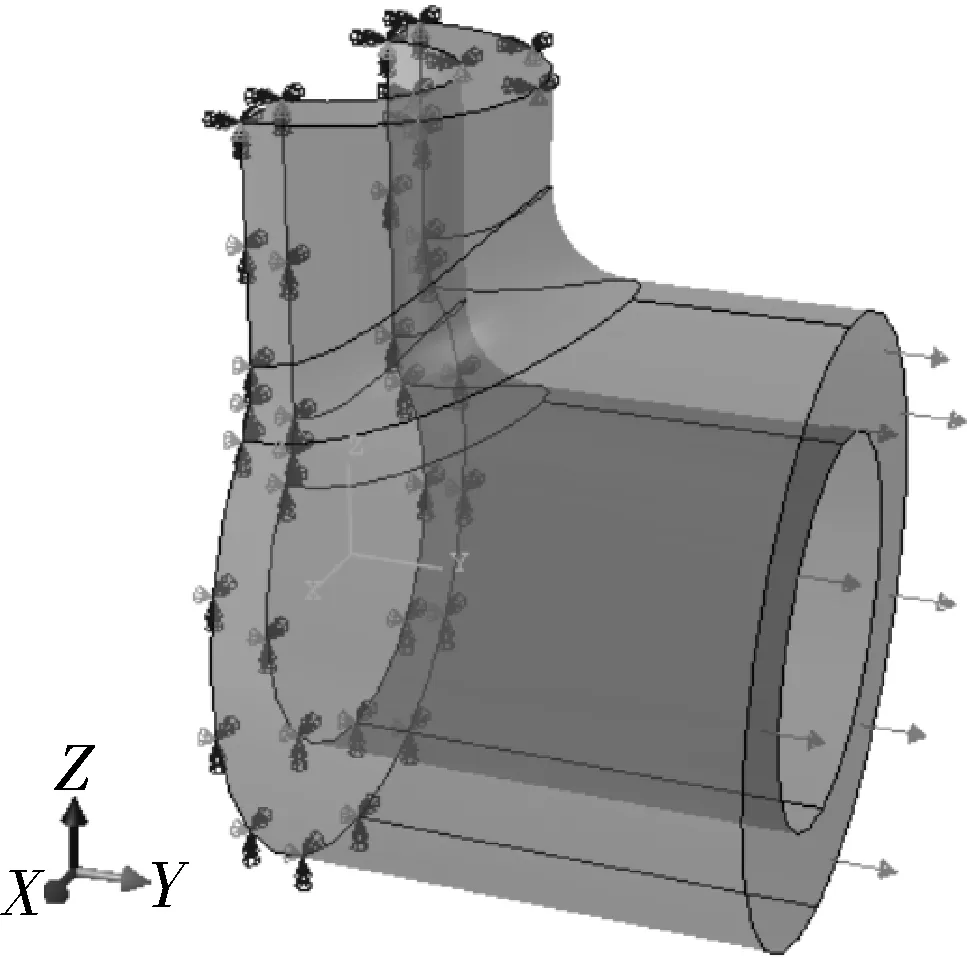
1.3 材料的性能

本次試驗的三通管件的材料為SA-335P91鋼，該鋼在576 ℃下的彈性模量為167 000 MPa，泊松比為0.3，熱膨脹系數為12.6×10-6/℃，且P91鋼在該溫度下的許用應力為82 MPa。因此，本次試驗定義：當三通管件的應力值≥82 MPa時，則為該管件的應力集中區域。

2 圖像處理方法

2.1 三通應力轉化為三維圖像

將有限元計算結果轉化為三維圖像主要有4個步驟：(1)計算數據導出；(2)網格單元與應力數據預處理；(3)應力數據非線性插值擬合；(4)應力切片圖輸出。

2.1.1 計算數據導出

經有限元模擬計算后，在內壓與軸向應力作用下，三通管件的應力分布如圖3所示。對網格單元節點的三維坐標及網格單元所對應的應力值進行導出，并以txt文件格式進行保存。

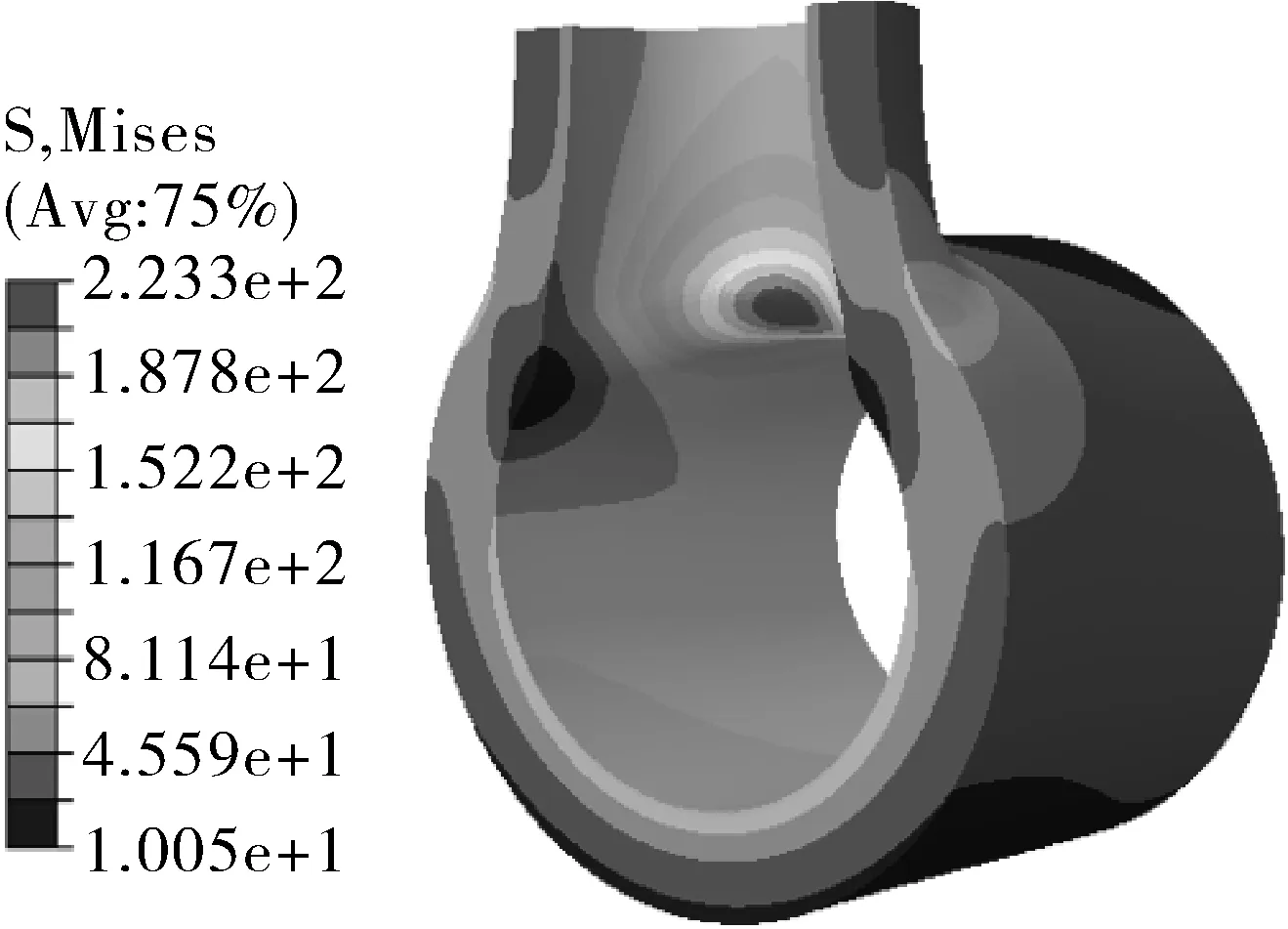
圖3 三通管件的應力分布Fig.3 Stress distribution of tee pipe fitting

2.1.2 網格單元與應力數據預處理

對有限元導出網格單元節點所映射的三維坐標進行平均求值，將網格單元平均后的三維坐標與其單元的應力相對應，并以矩陣的形式進行歸類，記為矩陣A。

2.1.3 應力數據非線性插值擬合

先將三通管件的模型導入Solidworks三維畫圖軟件，并以stl文件格式對三通管件模型進行導出；通過Avizo圖像處理分析軟件讀取stl文件[17]，由于stl文件格式的內容為三通管件的表面網格節點，因此須利用Avizo軟件的實體掃描模塊獲取模型的三維實體圖像，其過程示意見圖4。對三維實體模型的圖像進行賦值，此圖像中含三維模型的像素值為1，不包含三維模型區域的像素值為0，然后以3D tiff的圖像格式進行保存；通過Matlab對導出的3D tiff圖像進行讀取，得到三維矩陣B。用meshgrid函數生成尺寸大小與矩陣B相同的方位矩陣，即xq1，yq1，zq1。將矩陣B中等于0的區域對應于xq1，yq1，zq1矩陣相應區域的單元賦值為NaN；將通過數據處理后所得的有限元網格單元映射的三維坐標與應力相對應矩陣A及xq1，yq1，zq1三個方位矩陣，利用scatteredinterpolant 函數對其進行非線性擬合，得到三維矩陣D，矩陣D三維切片示意如圖5所示。

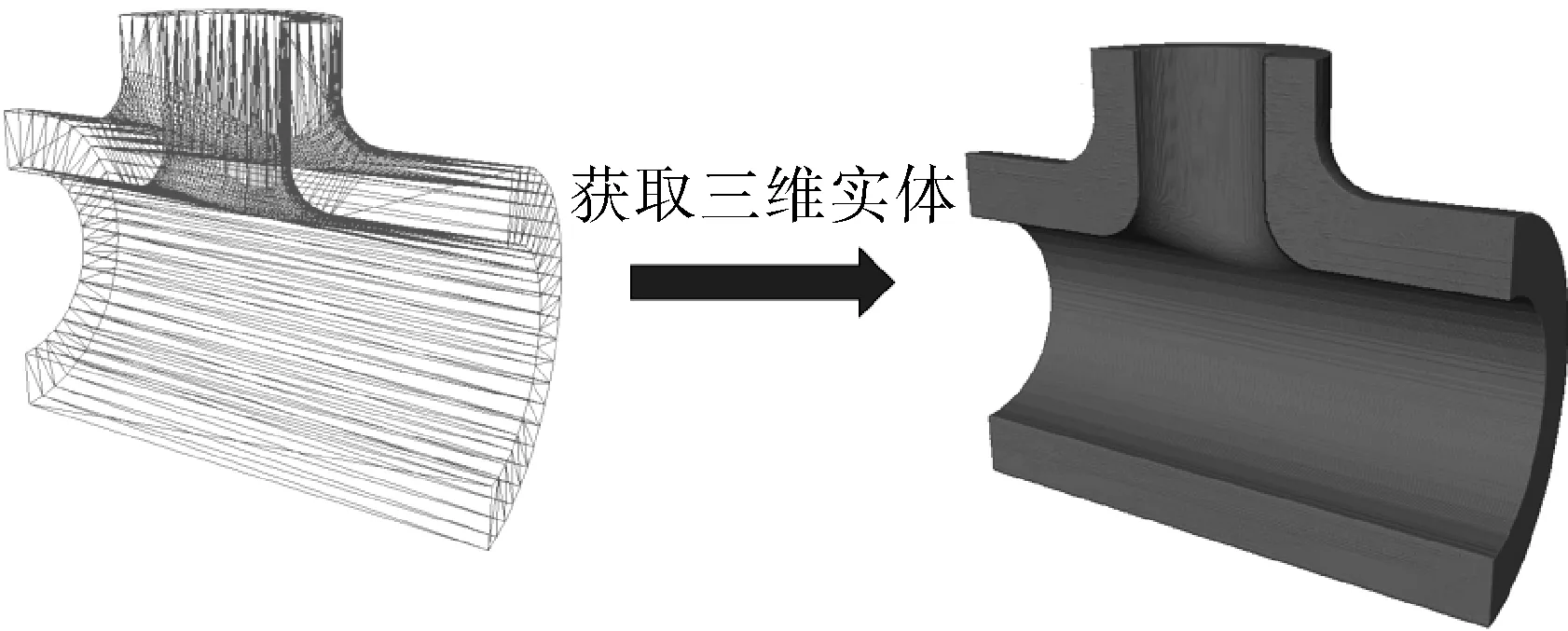
圖4 獲取實體三通管件示意Fig.4 Schematic diagram for obtaining solid tee pipe fittings

圖5 矩陣D三維切片示意Fig.5 Schematic diagram of 3D slice of matrix D

2.1.4 應力切片圖輸出

用Matlab 將進行非線性擬合所得的矩陣D，輸出數量為n3張的切片圖，其中，切片圖中像素點所對應的灰度值就是三通管件的應力值，如圖6所示。

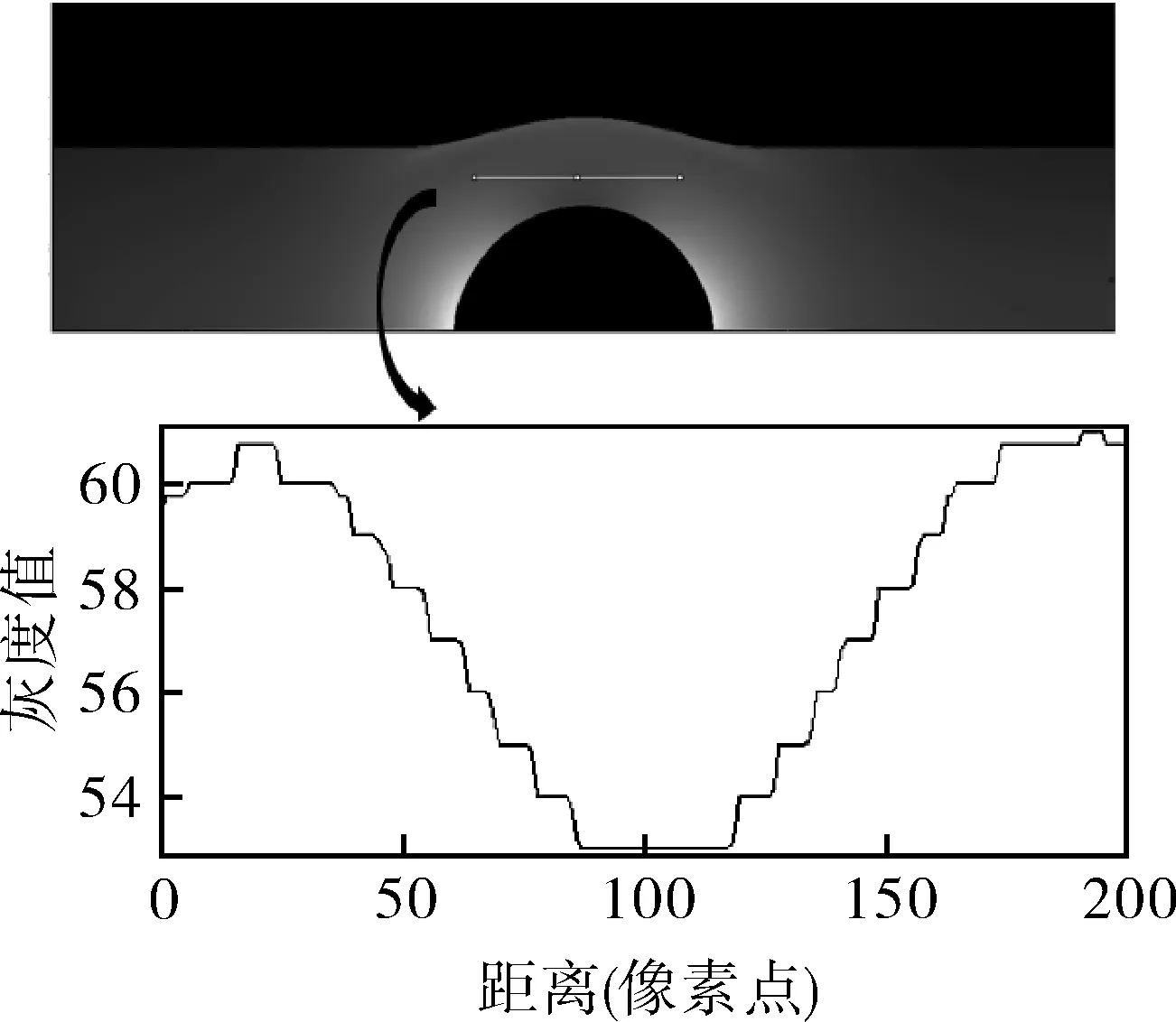
圖6 三通管件應力切片灰度圖Fig.6 Gray scale diagram of stress slice of tee pipe fittings

2.2 應力集中區域量化

通過圖像處理手段對三通的應力集中區域進行量化分析,包括借助閾值[18]和分水嶺分割的方法[19]對三通管道的應力集中區域進行分割提取，利用圖像便歷的方法對所提取的應力集中區域的應力點分布情況進行統計，采用二十六鄰域連通分割算法[20]計算其應力集中區域的體積。

3 結果分析

3.1 肩部應力集中區域分析

利用圖像處理方法對不同內圓角半徑三通的肩部應力集中區域進行提取和量化分析，提取示意見圖7。從圖8可以看出，隨著三通管道內圓角半徑r的增加，管道肩部內壁應力集中區域的最大等效應力與應力集中系數都呈先減小、后增加的趨勢；當內圓角半徑r=180 mm時，肩部應力集中區域的最大等效應力為249 MPa。

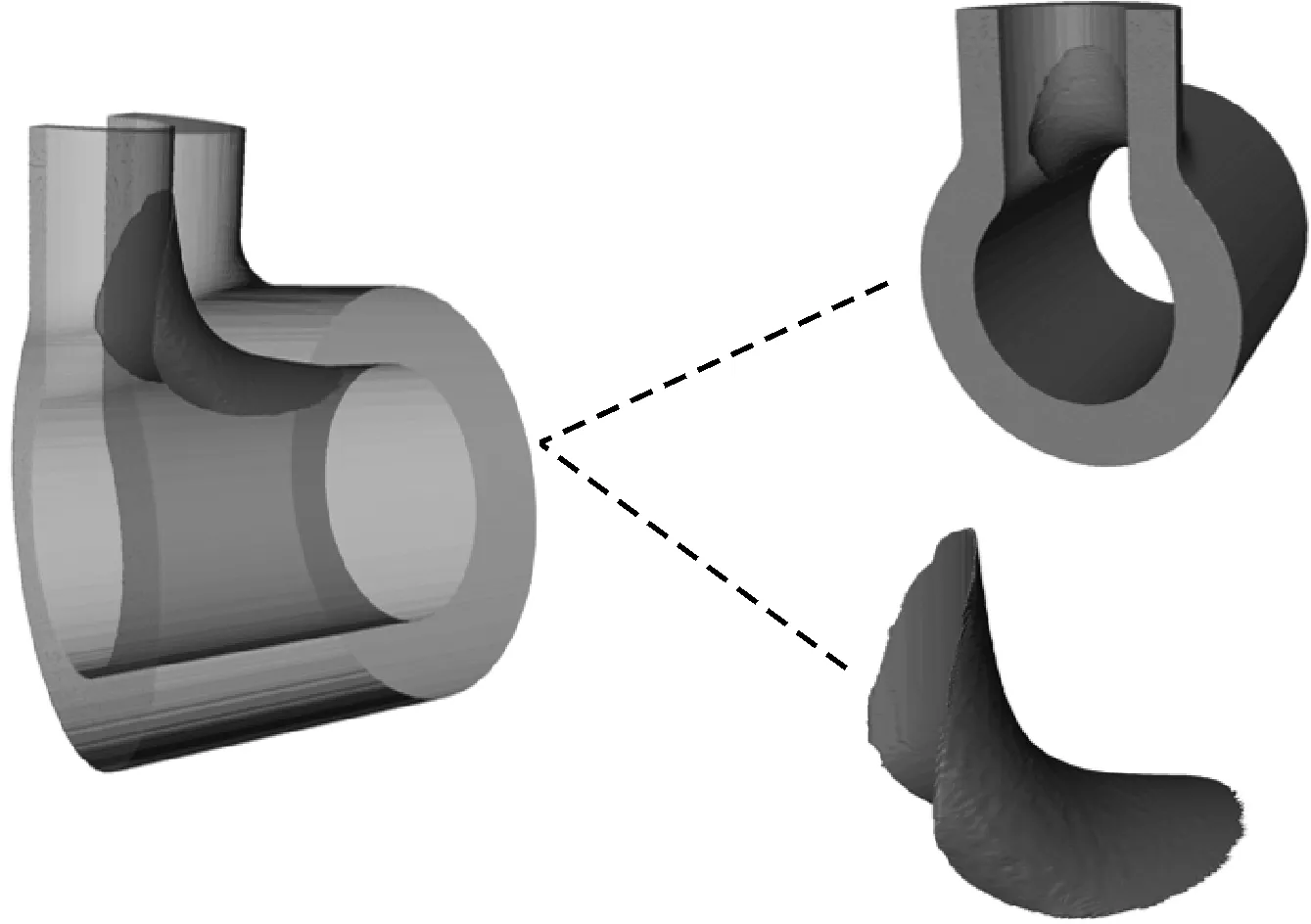
圖7 三通肩部應力集中區域提取示意Fig.7 Schematic diagram for extraction of stress concentrationarea on tee shoulder

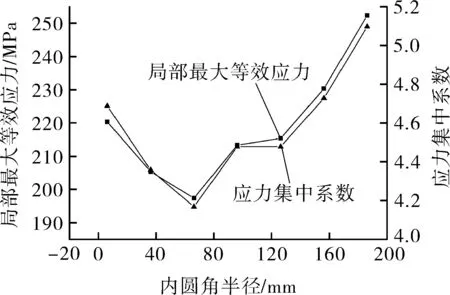
圖8 不同內圓角半徑三通的肩部最大等效應力、應力集中系數分布Fig.8 Distribution of maximum equivalent stress andstress concentration coefficient of shoulder of tee withdifferent inner fillet radius

基于二十六鄰域分割方法對不同內圓角半徑三通的肩部應力集中區域體積進行計算，其結果見圖9。可以看出，當三通管件的內圓角半徑不斷增大，肩部應力集中區域的體積也不斷地增加。

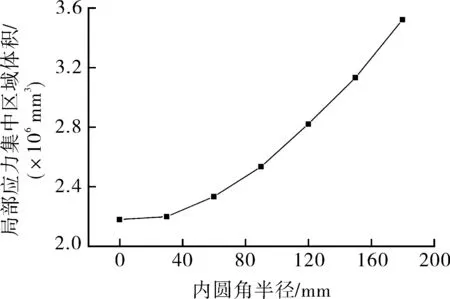
圖9 不同內圓角半徑三通的肩部應力集中區域的體積分布Fig.9 Volume distribution of shoulder stress concentrationarea of tee with different inner fillet radius

為進一步了解肩部內壁應力集中區域的應力情況，本次研究通過圖像便歷的方法，對不同內圓角半徑下三通的肩部應力集中區域的應力點分布進行統計分析，見圖10。

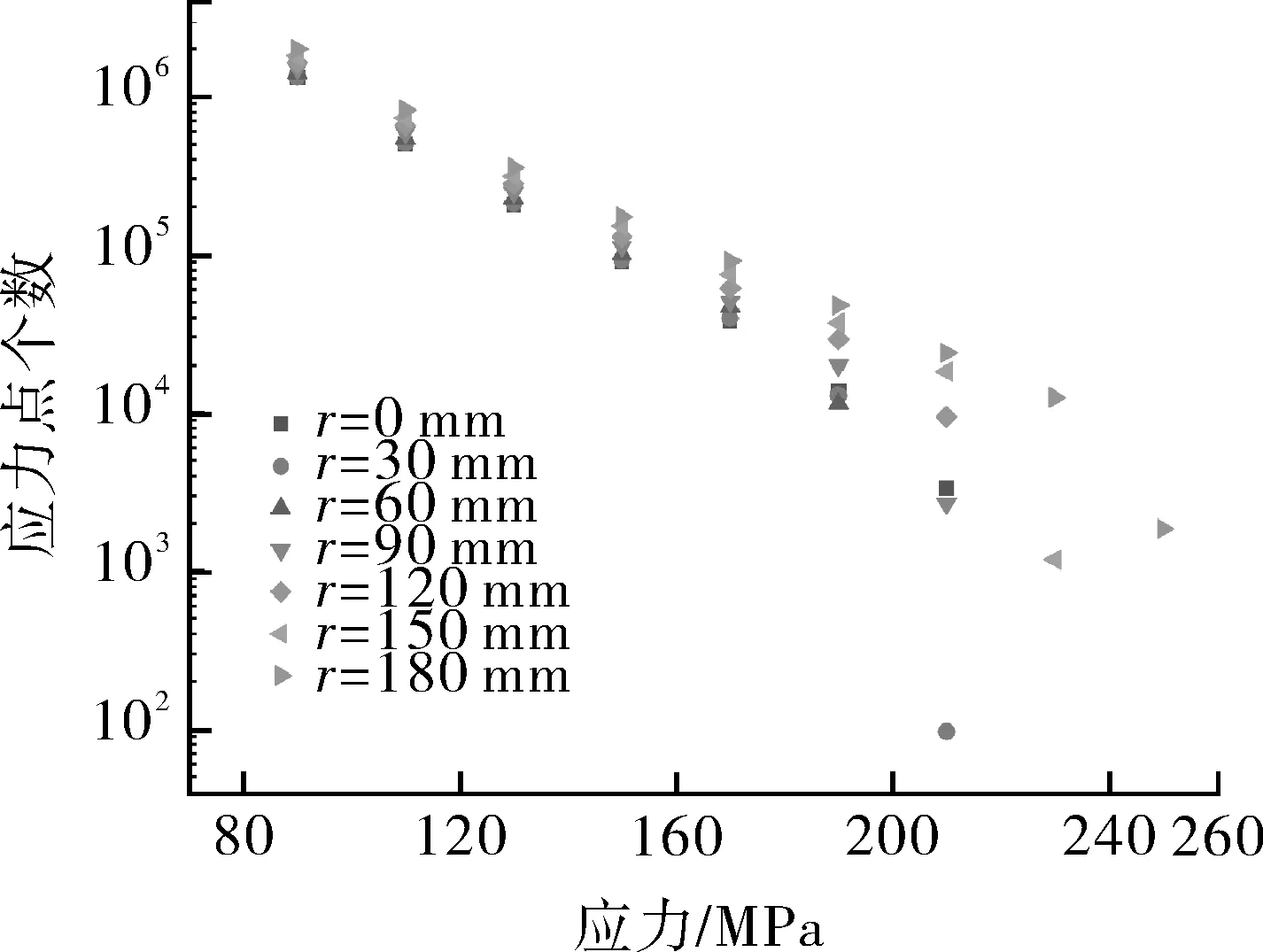
圖10 不同內圓角半徑三通肩部應力集中區域的應力點數量分布Fig.10 Quantity distribution of stress points in stressconcentration area of tee shoulder with different innerfillet radius

從圖10可看出，當三通內圓角半徑從r=0 mm增加至r=60 mm，管道肩部應力集中區域在較低應力范圍內的分布大致相同；但在高應力范圍內，隨著內圓角半徑的增加，應力集中區域的高應力點個數逐漸減小，即內圓角半徑增加，肩部應力集中區域的應力點個數在高應力區的分布逐漸減少；內圓角半徑從r=60 mm增至r=180 mm時，肩部應力集中區域在高應力區的應力點分布隨之增加，且在低應力區的應力點分布對比于內圓角半徑較小時也是增加，但增加的幅度小于高應力區。

本文采用閾值的方法將三通肩部內壁應力集中區域分為三部分，即閾值為82～100的應力場區域，100～150的應力場區域以及151-Smax(Smax為最大等效應力)的應力場區域。從圖11可以看出，三通肩部應力最集中的部位位于內壁的表面處，隨著距內壁表面距離的增加，其應力的集中程度不斷地減小。

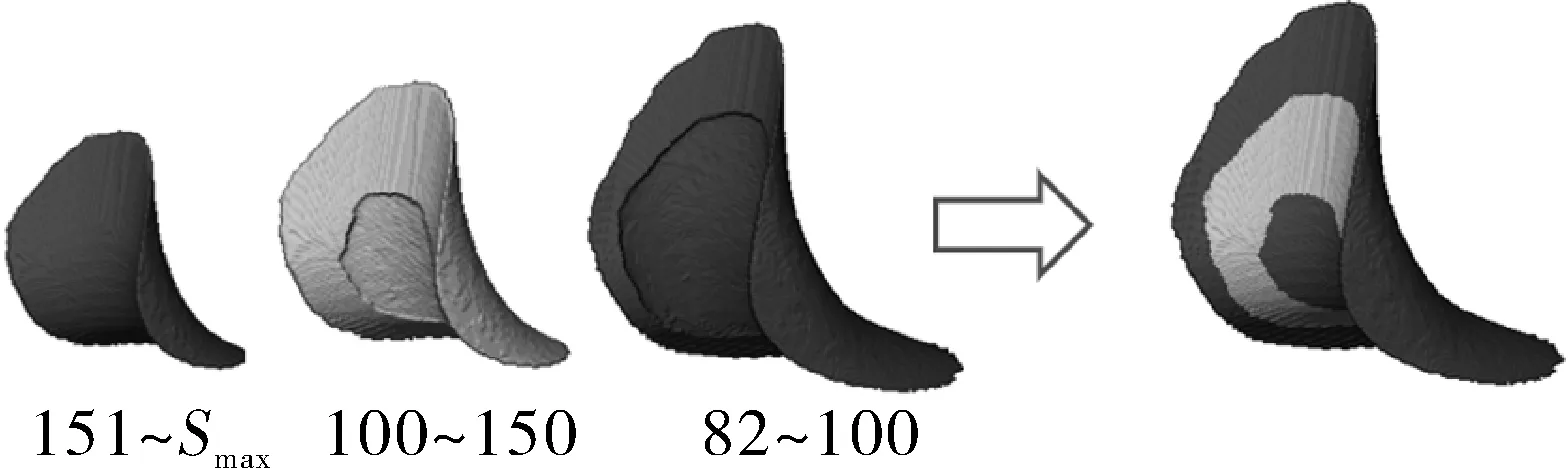
圖11 三通肩部應力集中區域分布示意Fig.11 Schematic diagram of distribution of stressconcentration areas on tee shoulder

由于閾值151-Smax為三通肩部內壁側應力最為集中的區域，對其進行具體的量化分析。從圖12(a)可以看出，隨著三通內圓角半徑增加，肩部內壁側高應力區的體積呈現減小后增加的趨勢。從圖12(b)可以看出，當內圓角半徑r=0增加至r=30 mm時，肩部高應力區的厚度呈增加的變化趨勢，隨之由r=30 mm增加至r= 90 mm時，高應力區的厚度隨著內圓角半徑的增加而減小，當r=90 mm增至r=180 mm時，內圓角半徑增加、高應力區的厚度隨之增加；肩部高應力區的面積隨著內圓角半徑的增加呈先減小、后增加的趨勢。

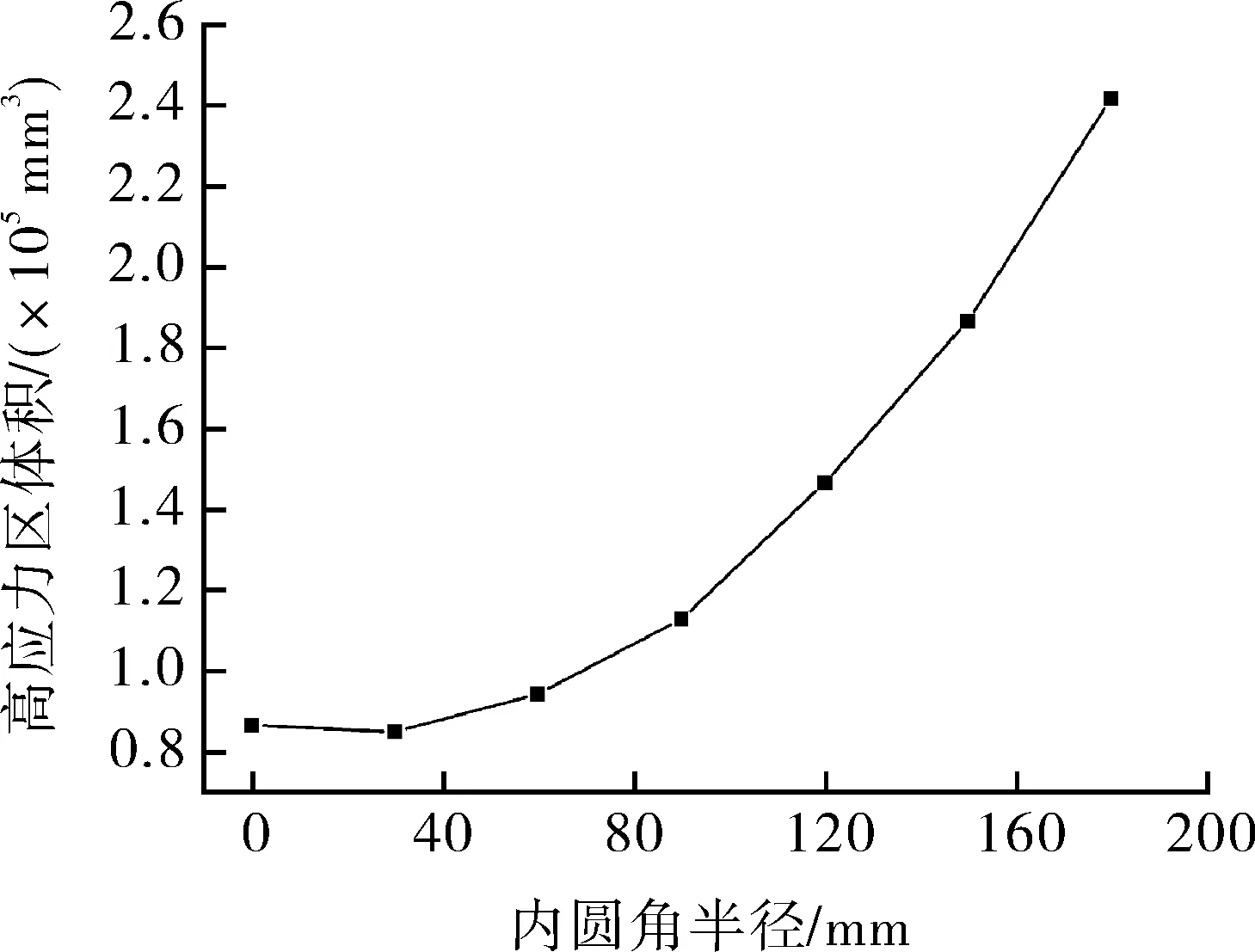
(a)肩部高應力區體積分布 (b)肩部高應力區表面積、厚度分布圖12 不同內圓角半徑三通肩部高應力區的體積、表面積與厚度分布Fig.12 Volume，surface area and thickness distribution of the high stress area on the shoulder of tee with differentinner fillet radius

本文定義a為高應力區的長度，與主管的軸向平行；b為高應力區的寬度，與支管的軸向平行。當三通內圓角半徑增加，高應力區的a，b隨內圓角半徑的變化見圖13。圓角半徑增加，高應力區的長度a并未發生明顯的變化，但其高應力區的寬度b隨內圓角半徑的增加呈線性增加的趨勢。

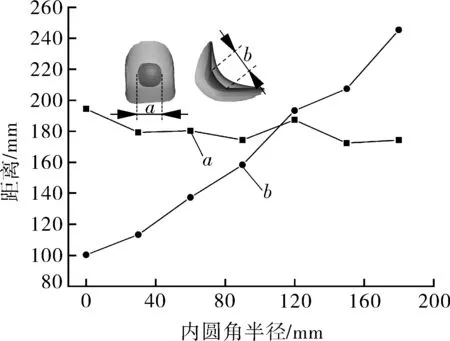
圖13 不同內圓角半徑三通肩部高應力區的長、寬分布Fig.13 The length and width distribution of the high stressarea in tee shoulders with different inner fillet radii

綜合上述研究表明，適當地增加三通內圓角半徑能減小肩部的應力集中程度，三通的內圓角半徑從r=0 mm增至r=60 mm，能降低肩部應力集中區域的應力集中程度，但當r>60 mm時，圓角半徑的增加反而會導致三通肩部應力集中區域的應力更為集中。隨著內圓角半徑的變化，應力集中區域的形狀和位置發生不同程度的改變。從圖12,13可以看出，隨著內圓角半徑的增加，表面積和寬度b呈整體增加的趨勢，由于支管壁厚相較于主管的壁厚更薄，因此，導致支管處開裂的幾率增加。

3.2 腹部應力集中區域分析

用圖像處理的方法對三通管道腹部位置的應力集中區域進行提取，如圖14所示(圖中B區域為三通管件腹部位置的應力集中區域)。從圖15(a)可以看出，隨著三通管道外圓角半徑增加，三通管道腹部外壁應力集中區域的最大等效應力與應力集中系數都呈先增大、后減小的趨勢。三通外圓角半徑R=30 mm時，其腹部應力集中區域的最大等效應力最大，為99 MPa。

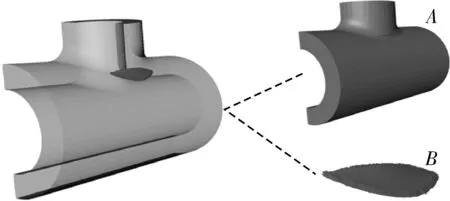
圖14 三通腹部應力集中區域提取示意Fig.14 Schematic diagram for extraction of stressconcentration area on tee abdomen

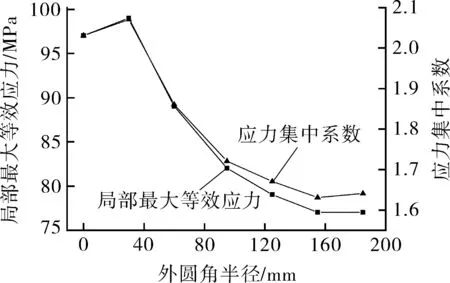
(a)三通腹部最大等效應力、應力集中系數分布

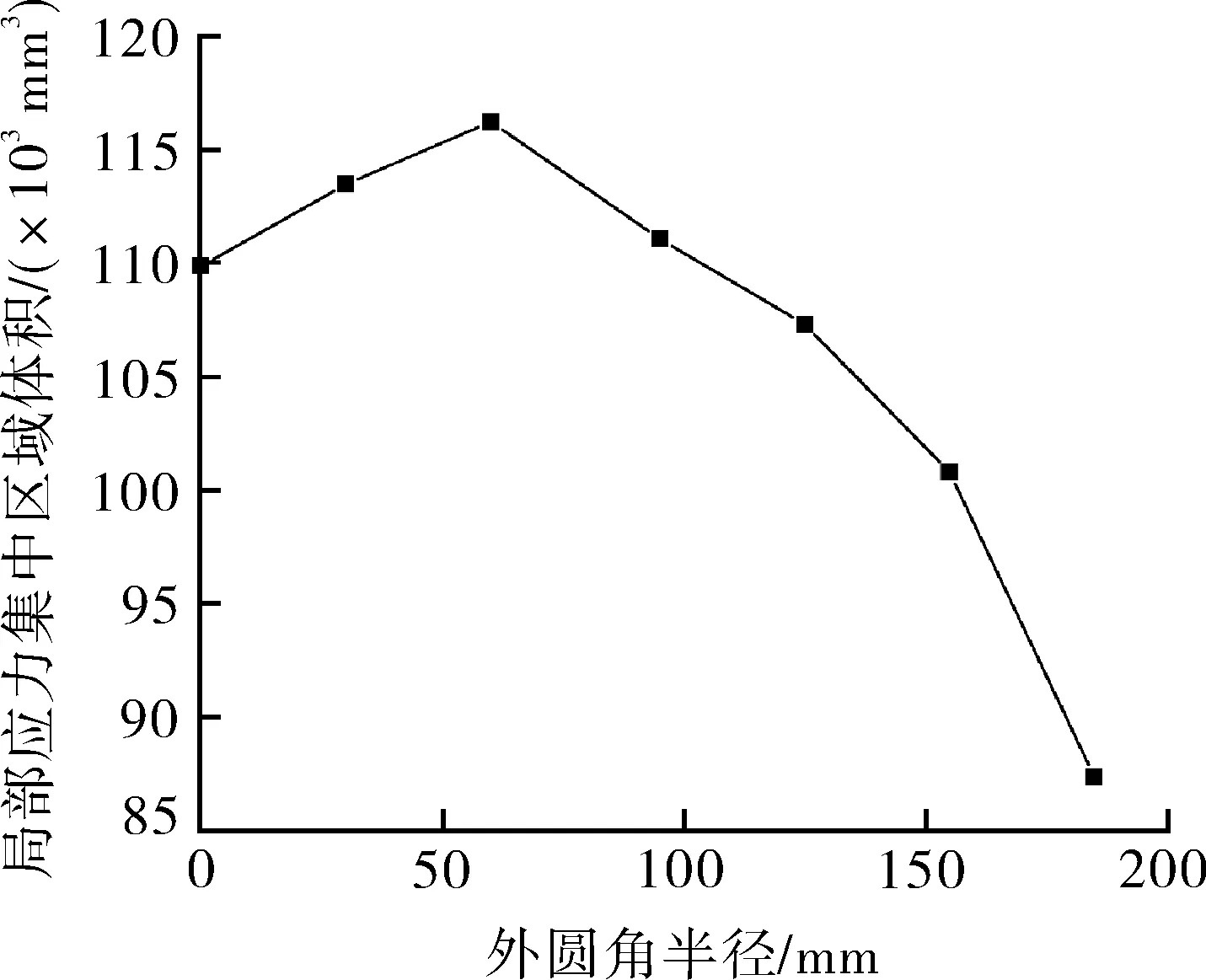
(b)三通腹部應力集中區域的體積分布圖15 不同外圓角半徑三通腹部應力集中區域量化圖Fig.15 Quantitative map of stress concentration area inabdomen of tee with different radius of outer fillet

三通腹部位置應力集中區域的體積也呈相同的變化趨勢，當R=0～60 mm時，腹部應力集中區域的體積隨著外圓角半徑的增大而增大，當外圓角半徑繼續增大時，腹部應力集中區域的體積隨之減小，見圖15(b)。

利用圖像便歷的方法對三通腹部位置應力集中區域的應力點分布情況進行量化分析，其結果如圖16所示。當外圓角半徑R=30 mm時，腹部位置應力集中區域在高應力區的應力點數量大于R=0 mm 時的應力點，隨著外圓角半徑繼續增大，腹部位置應力集中區在高應力區的應力點個數逐漸下降，外圓角半徑增至R=185 mm時，腹部位置高應力區的應力點數量有增加的趨勢，但幅度不大。

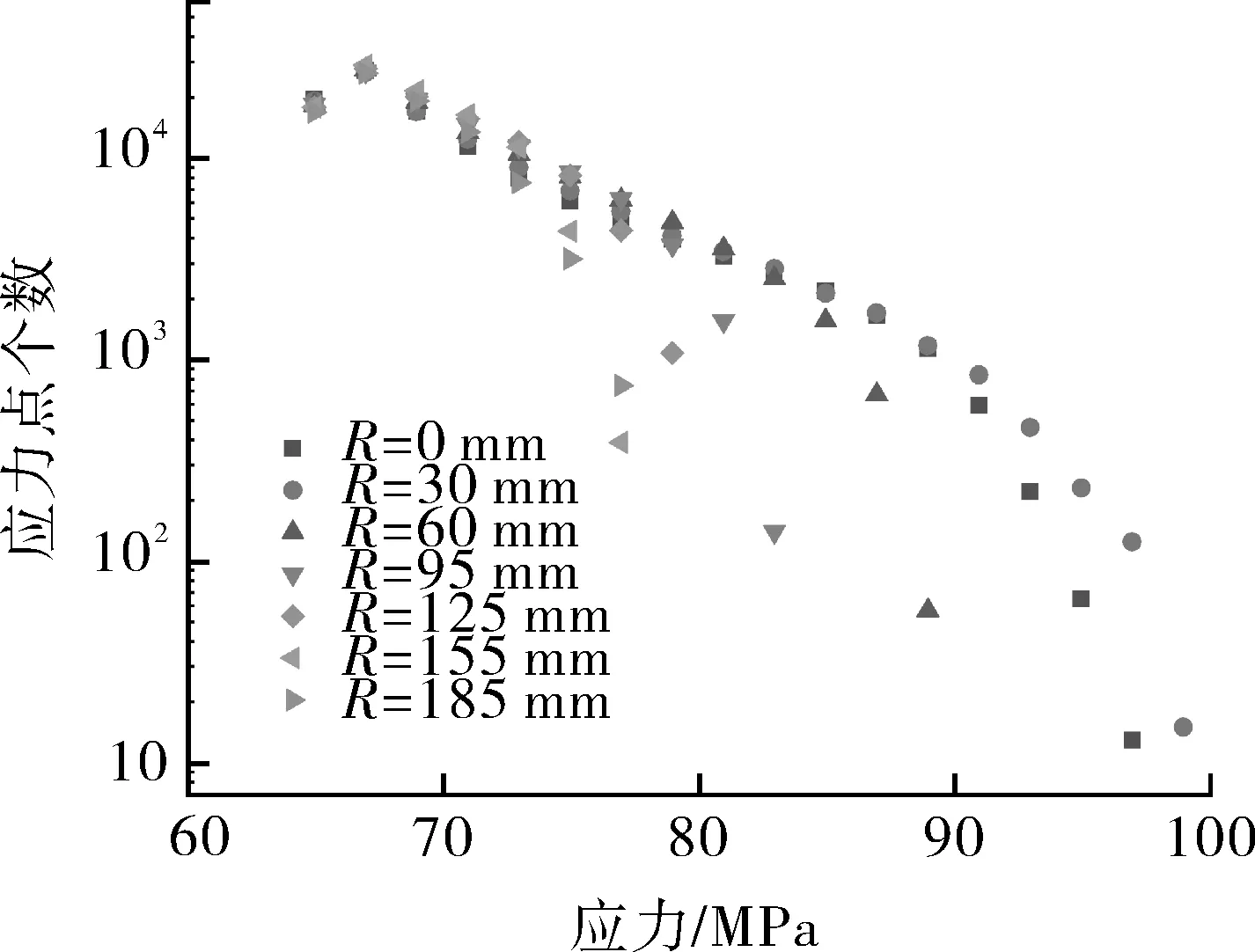
圖16 不同外圓角半徑三通腹部應力集中區域的應力點數量分布Fig.16 The distribution of number of stress points inthe stress concentration area of the abdomen of the teewith different radius of outer fillet

為進一步探究三通腹部位置應力集中區域的應力情況并對其進行合理的安全評估，本次試驗對腹部位置應力集中區的長度a(平行于主管軸向)、寬度b(與支管軸向平行)進行了測量分析，如圖17所示。可以看出，隨著三通管件外圓角半徑的增加，腹部位置應力集中區的a，b并沒有發生明顯的變化，表明三通管件外圓角半徑的變化對腹部位置應力集中區的形狀變化影響不大。

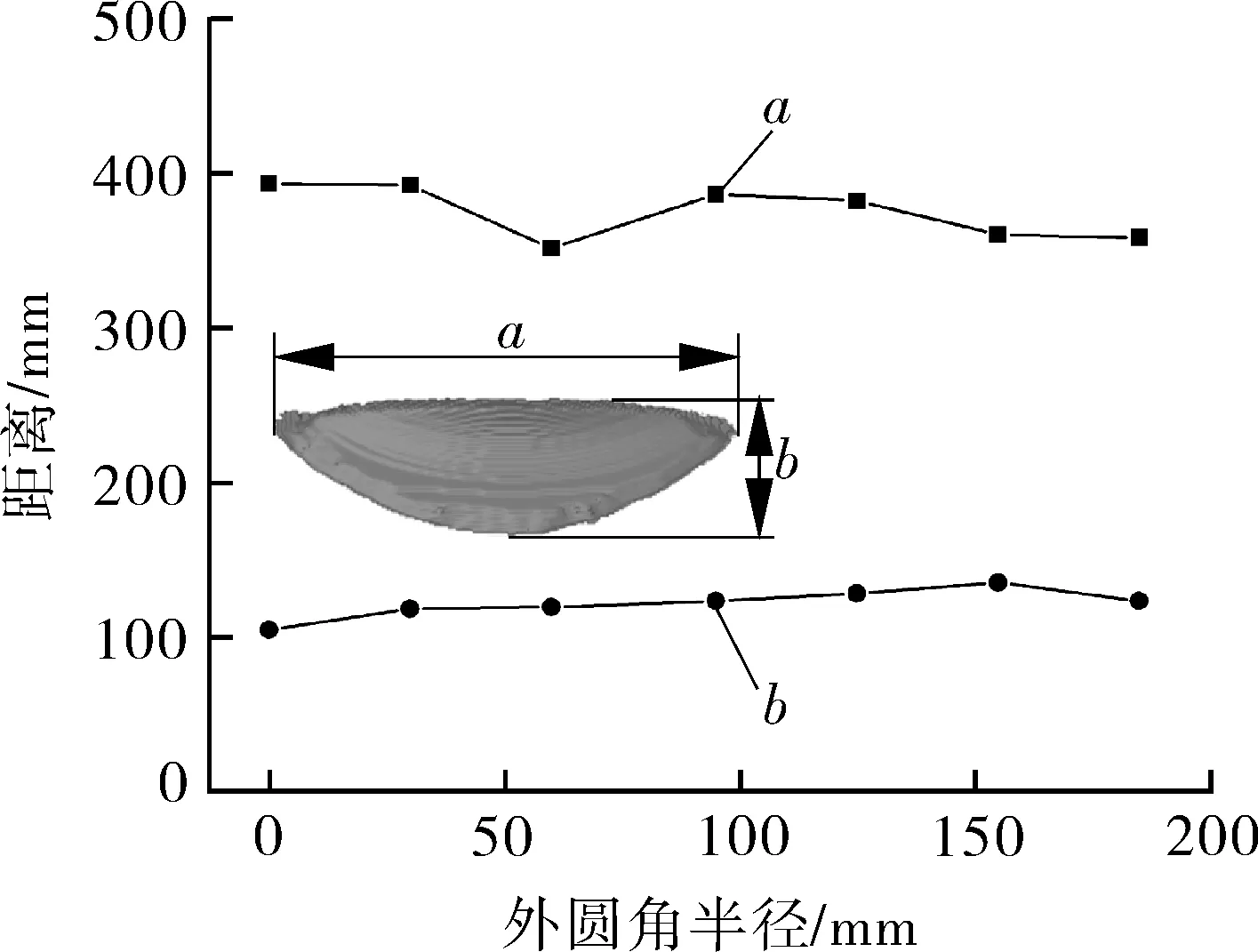
圖17 不同外圓角半徑三通腹部高應力區的長、寬分布Fig.17 The length and width distribution of the high stressarea in the abdomen of the tee with different radiusof outer fillet

通過對腹部位置應力集中區域的表面積、厚度量化分析(見圖18)可知，當三通管件外圓角半徑從R=0 mm增至R=95 mm，腹部應力集中區域的表面積逐漸增加，外圓角半徑繼續增加，其腹部應力集中區域的表面積開始下降；腹部應力集中區域的厚度隨著外圓角半徑增加呈下降的趨勢。

圖18 不同外圓角半徑三通腹部高應力區的表面積與厚度分布Fig.18 Surface area and thickness distribution of high-stress area in abdomen of tee with different radius ofouter fillet

綜合上述結果表明，增大三通管件的外圓角半徑能有效地降低三通管件腹部位置的應力集中程度。增大外圓角半徑的主要作用是降低腹部位置高應力區的應力分布及腹部位置應力集中區域的厚度。但是當外圓角半徑過小時(R≤30 mm)，增加外圓角半徑，反而會增加三通腹部應力集中區域的最大等效應力、應力集中系數、應力集中區域的體積及表面積。

4 結論

本文基于有限元分析，探究了不同圓角半徑對三通應力集中區域的影響。用圖像處理方法對異徑三通的應力集中區域進行提取，并將三通的肩部、腹部位置的應力集中區域進行量化分析，有效地對該類異徑三通管件安全性能進行評估，為改善熱擠壓三通的生產工藝提出合理的建議。具體結論如下。

(1)對于異徑三通肩部位置的應力集中區域，適當增加三通的內圓角半徑(r≤60 mm)能降低肩部位置的應力集中程度，但其應力集中區域的形狀并不相同，隨著內圓角半徑(r>60 mm)增大，高應力區的寬度b、表面積與厚度呈整體增加的趨勢，同時在肩部區域的應力更加集中，導致三通在支管處開裂的幾率增加。

(2)增大異徑三通管件的外圓角半徑，以減小腹部應力集中區域的厚度以及腹部應力集中區域在高應力區的應力點數量來有效降低三通管件腹部位置的應力集中程度，但是當外圓角半徑R≤30 mm時，外圓角半徑的增加對降低腹部位置的應力集中程度并不明顯，反而會導致該區域最大等效應力與表面積增加，使三通管件腹部位置失效的幾率增加。

(3)對于此類結構與工況的三通，適當增加內圓角半徑(r≤60 mm),能有效地緩解三通肩部位置的應力集中程度，但支管需保證足夠的安全壁厚。對于緩解三通腹部位置的應力集中程度，需增加一定量的外圓角半徑(R≥30 mm)。