鎢極氬弧焊熱輸入與面積稀釋率關系的探討

郭 梟，徐 鍇，呂曉春，陳佩寅，陳 波，霍樹斌

(1.哈爾濱焊接研究院有限公司，哈爾濱 150028；2.哈爾濱威爾焊接有限責任公司，哈爾濱 150028)

0 引言

焊縫稀釋率對焊接接頭的質量與服役性能有非常重要的影響[1]。不同的場合對于稀釋率的控制要求不盡相同，如厚件焊接時,期望熱輸入一定時稀釋率較大；而異種鋼焊接時，較小的稀釋率為宜[2]。

目前，針對稀釋率的影響與預測研究主要以工藝參數、熱輸入與稀釋率之間關系的算法優化為主，已有學者[3-7]分別采用遺傳神經網絡、Elman 網格算法、響應曲面法、統計分析等不同算法，建立了通過焊接電流、焊接速度等工藝參數預測稀釋率的模型。 文獻[2]采用統計分析方法，研究了極性、送絲速度、焊接速度、電壓四因素耦合對埋弧焊熱輸入、稀釋率、熱影響區寬度的影響規律，結果表明焊接熱輸入對稀釋率的影響不明顯。 焊接工藝參數對稀釋率影響具有雙重作用[3]，以焊接速度為例，增大焊接速度，一方面會降低母材、焊絲總熱輸入，從而使稀釋率降低；另一方面又會減小單位長度焊縫上焊絲的熔敷量，使稀釋率增大，兩方面綜合作用使焊接速度對稀釋率的影響作用難以預測。 文獻[4]采用Elman網格算法預測稀釋率，結果表明，隨著堆焊速度的增加，稀釋率變化不大。 同樣，熱輸入對稀釋率的影響也是雙重的，熱輸入增大時，作用于母材、填充金屬的熱輸入均增加，熱輸入對稀釋率的影響難以預測。 目前對稀釋率的本質缺乏全面研究，焊接熱輸入作用于母材熔化、填充金屬熔化、熱影響區的比例尚無相關報道，同時，傳統的熱輸入公式存在諸多不足，如未考慮填充金屬作用、難以直接與稀釋率建立關系等。 采用傳統公式研究熱輸入與稀釋率的關系容易得出相反的結論[8-9]。

文中對稀釋率本質、傳統熱輸入的不足進行分析，對傳統熱輸入公式進行分解細化，采用JMatPro計算密度、比熱等熱物理性能，并計算單位體積填充金屬需要的熱量qfm，對熱輸入與稀釋率的關系進行推導，建立由熱輸入預測稀釋率的公式，并通過試驗對預測公式進行驗證。

1 試驗方法

驗證試驗用焊接材料采用實驗室試制?1.2 mm 的ERNiCrFe-13型鎳基合金焊絲，其化學成分具體見表1。采用鎢極氬弧焊(GTAW)工藝在規格為300 mm×300 mm×40 mm的Q235鋼板上進行堆焊，堆焊尺寸約為200 mm×200 mm×20 mm的塊狀金屬。 對表面進行磨削加工后，在表面進行單道焊驗證試驗(見圖1)，具體工藝參數見表2。對焊道5個橫截面面積進行測量，求取面積算術平均值。

表1 試驗用焊絲化學成分Tab.1 Chemical composition of experimental wire %

表2 驗證試驗焊接工藝參數Tab.2 Welding process parameters for verifying test

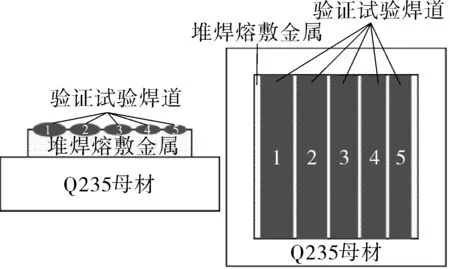
圖1 驗證焊接試驗示意Fig.1 Schematic diagram of verifying welding test

2 分析與推導

2.1 傳統熱輸入、功率比公式的不足

ASME第Ⅺ卷QW-409.29節給出了GTAW的傳統的熱輸入Q計算公式：

(1)

傳統的熱輸入Q主要考慮焊接電源的輸出功率和焊接速度。 實際過程中，基于熱效率考慮，提出Qeff公式如下：

(2)

式中,μeff為熱效率系數，對于GTAW工藝,μeff一般為0.7～0.9[10]。

TATMAN[9]采用自主研發的自動液氮量熱系統精確測定了TIG焊的熱效率μeff，本文選取測定值的平均值μeff=0.85。對于GTAW工藝，焊接電弧不僅作用于母材，還用于熔化填充金屬，式(2)實際為焊接電源的有效熱輸入，并未區分Qeff分別作用于母材、填充金屬的大小，在研究熱輸入對稀釋率、組織、性能的影響時，送絲量的影響被忽略，利用Qeff研究熱輸入對組織、性能的影響時，可能會得出相反的結論。

ASME第Ⅺ卷QW-409.29節給出了GTAW的另一種熱輸入估算公式，即功率比PR(Power Ratio)，具體公式如下：

(3)

式中,PR為功率比，W/cm2;vfs為送絲速度，cm/s;Awire為焊絲的橫截面面積，cm2。

功率比PR綜合考慮了焊接熱源、焊接速度、填充金屬送絲速度，假設焊縫全部由填充金屬形成，物理意義為單位面積焊縫橫截面的功率。 顯然這與實際情況存在差異，由于忽略了熔化母材的影響，難以建立PR與稀釋率的關系。

2.2 熱輸入與面積稀釋率關系公式推導

稀釋率指焊接過程中，由于母材熔化混入熔池而引起焊縫金屬成分的變化程度，用母材在焊縫中所占的百分比表示。 目前計算稀釋率的方法主要包括面積稀釋率、化學成分稀釋率、厚度稀釋率3種[11-13]。

本文稀釋率采用面積百分比δarea表示，即熔化母材的橫截面面積在整個焊縫橫截面面積所占的百分比，具體示意圖見圖2。稀釋率δarea計算公式[14]如下：

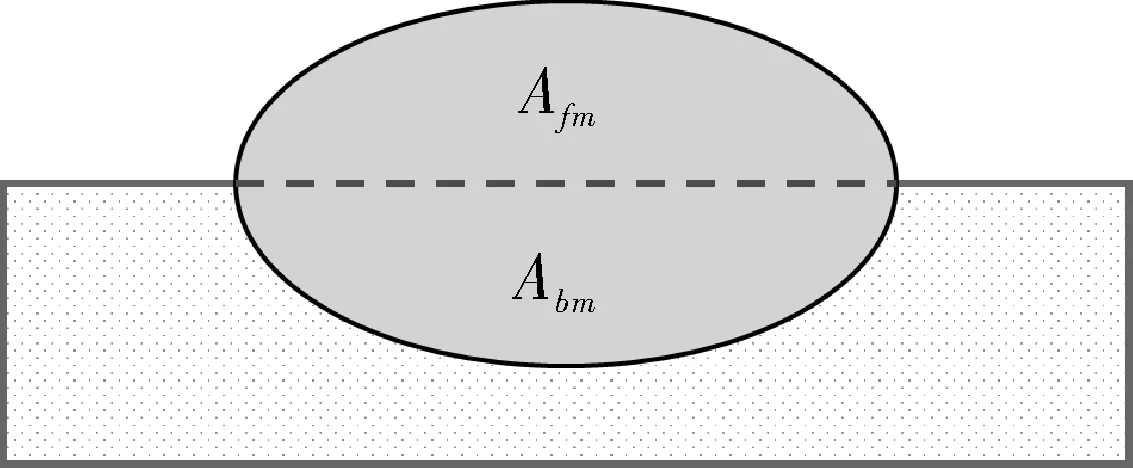
圖2 稀釋δarea定義Fig.2 Definition of dilution δarea

(4)

式中，Abm為焊縫中熔化的母材部分橫截面面積，mm2;Afm為焊縫余高部分橫截面面積，mm2。

有效焊接熱輸入Qeff主要作用于母材與填充金屬，其公式如下：

Qeff=Qfm+Qbm

(5)

式中,Qfm為熔化填充金屬需要的熱輸入，kJ/cm;Qbm為作用于母材的熱輸入，kJ/cm。

(1)余高部分Afm與Qfm。

Afm為填充金屬熔化后形成焊縫部分面積，其可由下式求出：

(6)

按照表2中參數對不同焊接速度的下Afm進行計算，計算值Afm-calc與測量值Afm-test結果如圖3所示,可以看出，預測值與實測值基本一致。

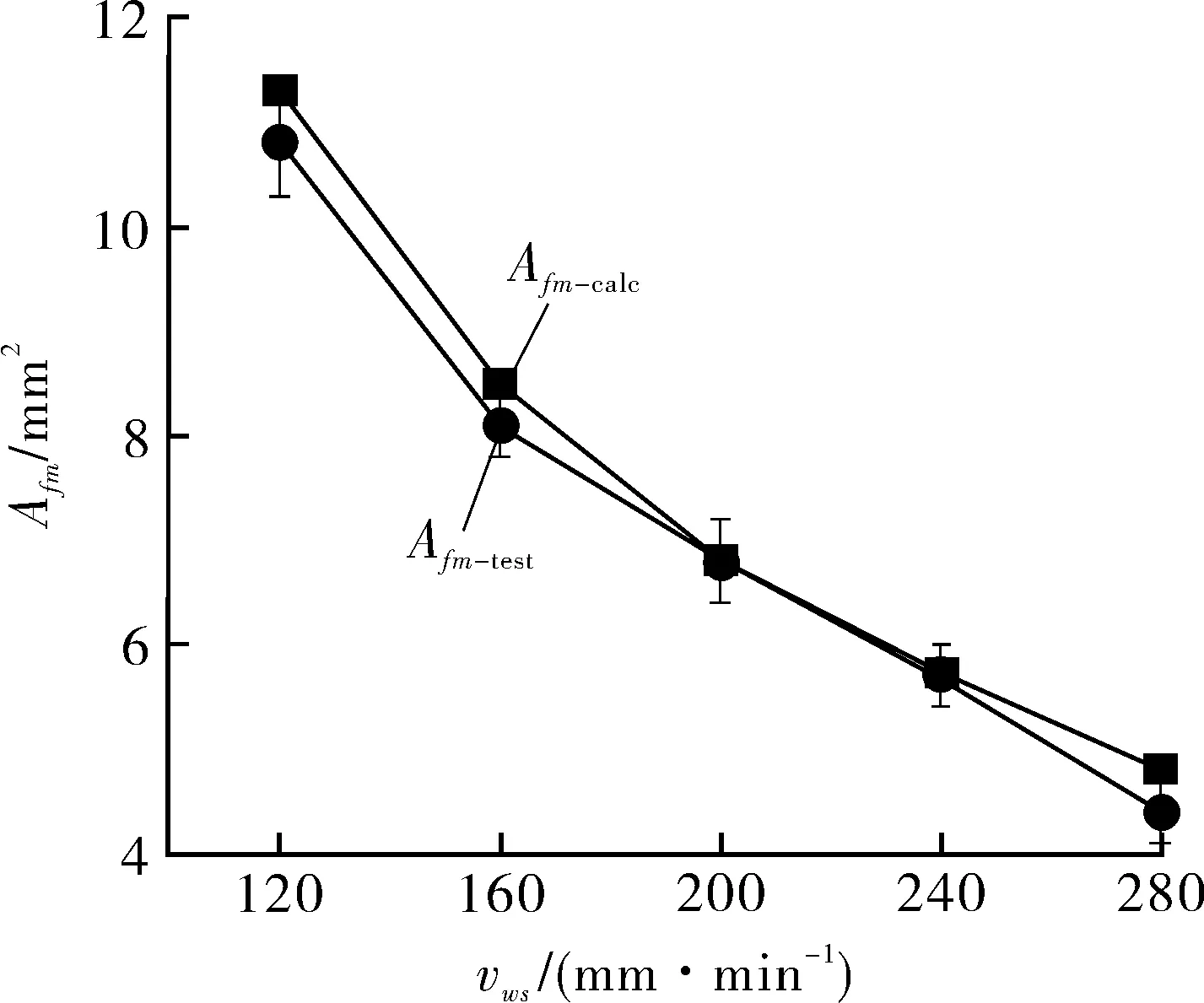
圖3 Afm預測驗證結果Fig.3 Verification results for Afm prediction

Qfm為作用于填充金屬的熱輸入，主要用于熔化填充金屬，為簡化計算，忽略電阻熱、對流散熱等其他影響，即全部用于熔化填充金屬，因此Qfm等效為熔化填充金屬需要的熱輸入。為實現Qfm計算，需要將常用的質量比熱容cfm轉變為體積比熱容sfm，即:

sfm=cfmρfm

(7)

式中,sfm為體積比熱容，J/(cm3·℃);cfm為質量比熱容，J/(g·℃);ρfm為密度，g/cm3。

則熔化單位體積填充金屬需要的熱量qfm為:

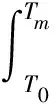
(8)

式中，Tm為熔點,℃;T0為室溫，℃。

基于表1中化學成分，采用JMatPro進行材料cfmρfm熱物理性能計算，然后利用Origin軟件，按照公式(8)求取qfm，其值大小對應圖4中陰影部分的面積值，求取陰影部分面積，可知qfm=7 903 J/(cm3·℃)。

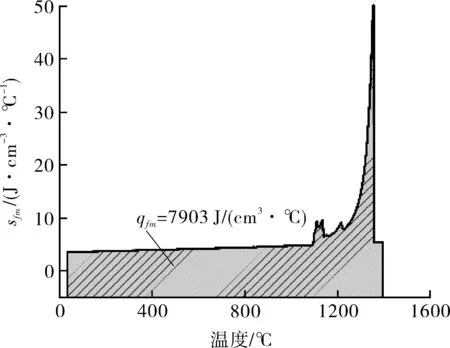
圖4 體積比熱容sfm隨溫度變化趨勢Fig.4 Variation trend of temperature with volumetricspecific heat capacity sfm

則焊接過程中用于熔化填充金屬的熱輸入Qfm公式如下：

Qfm=qfmAfm

(9)

(2)母材Abm與Qbm。

對于母材的熔化面積Abm，無法通過類似式(6)的方法求出，需要在對Qbm分析的基礎上，結合式(5)反推求出。 作用于母材的Qbm中用于熔化母材的部分為Qmbm，假設熔化系數μm為固定值，μm物理意義為Qbm在Qmbm中的占比，則有下式：

Qmbm=μmQbm

(10)

作用于母材的熱輸入Qbm可由式(5)求出。 同時Qmbm還滿足式(11)，母材為熔敷金屬，所以qbm=qfm。 對于μm，則可由式(12)求出。

Qmbm=qbmAbm

(11)

(12)

圖5示出根據不同焊道測量出的母材熔化面積Abm以及根據公式(12)估算出的μm。 可以看出，隨著焊接速度vws的增加，母材熔化面積Abm顯著減小，估算的μm變化不大，取均值μm=0.12。

圖5 不同焊接速度vws下的Abm,μmFig.5 Abm and μm at different welding speed vws

結合公式(4)(9)(10)可推導出公式(13),利用式(13),便可以用熱輸入Qeff和Qfm預測稀釋率。

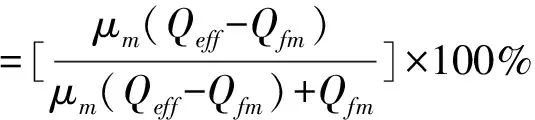
(13)

3 試驗驗證

設計了不同焊接速度下的試驗對上述推導公式(13)進行驗證，圖6示出不同焊接速度下的焊道截面。 各焊道統計5組焊道截面的數據，統計結果見表3。

圖6 不同焊接速度下的焊道橫截面Fig.6 Weld bead cross section at different welding speed

由表3可以看出，稀釋率預測值與測量值的誤差在±5%內，吻合度較好，且隨著有效熱輸入的減小，稀釋率逐漸減小。

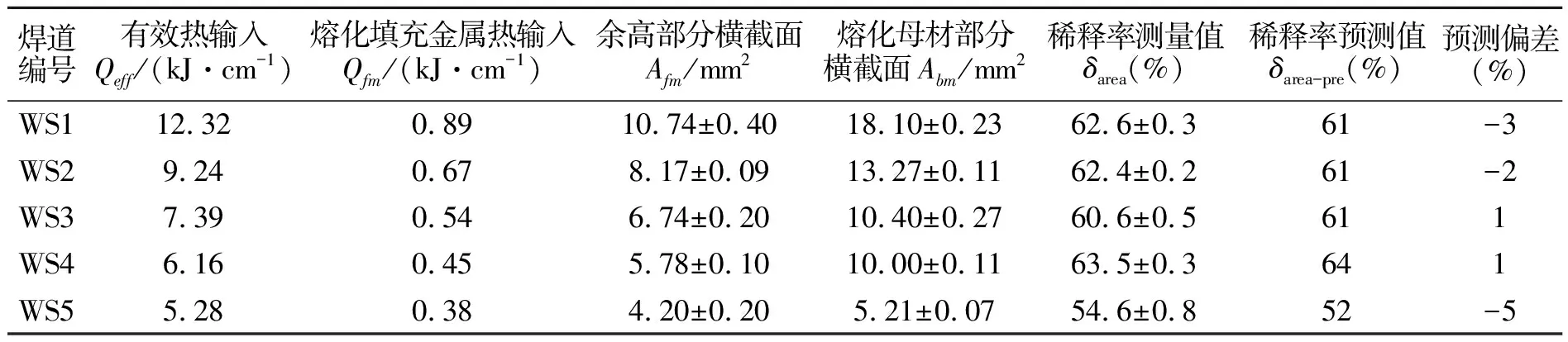
表3 稀釋率驗證試驗結果Tab.3 Test results of dilution verification

4 結論

(1)通過公式推導，建立了利用熱輸入Qeff預測稀釋率δarea-pre的公式(見式(13))。

(2)結合JMatPro熱物理性能計算結果、試驗測量，計算出熔化單位體積填充金屬需要的熱量qfm與熔化系數μm，分別為qfm=7 903 J/(cm3·℃),μm=0.12。

(3)通過試驗對公式(13)進行了驗證，結果顯示計算的稀釋率與試驗實測值誤差在±5%以內，吻合度較好。