纖維纏繞Kagome網格衛星承力筒承載性能分析及結構優化研究*

孫守政，孫天峰，陳維強，范東興，韓振宇，富宏亞

（1.哈爾濱工業大學，哈爾濱 150001；2.中國空間技術研究院北京衛星制造廠有限公司，北京 100094）

碳纖維增強型復合材料具有輕質、高強、耐腐蝕、極端環境適應性好、可設計性強等特點，被廣泛應用于航空航天、能源開采、建筑、交通等多個領域中[1–2]。在航空航天領域，復合材料可以替代傳統鋁合金、鈦合金等金屬構件，既減輕了質量，又提升了構件的可靠性。國外將復合材料使用率作為評價飛機先進程度的重要指標。例如，在波音787客機機翼及機身上所使用的復合材料比重可達50%，而上代波音777客機僅使用了12%的復合材料，由此可見，復合材料已經成為航空航天領域無法替代的應用材料，在國家“大飛機”、“載人航天與探月工程”、“天問一號”、“北斗衛星導航”等重大工程中的作用越來越突出[3–4]。承力筒是衛星中的重要承力部件，對衛星總體力學性能及服役性能至關重要。衛星承力筒的設計與結構優化是進一步減輕重量、提升承力結構及承載性能的重要前提[5]。航空航天結構件設計中，有兩種基本的復合材料結構設計思想：一是基于承載蒙皮縱梁加強結構和蜂窩夾層結構；二是無蒙皮的網格加強結構。相較于承載效率而言，無蒙皮的網格結構所受載荷完全由相互交錯的加強筋承受，因而其承載效率高于有蒙皮的縱梁加強結構和蜂窩夾層結構。早期的網格加強結構通過機械加工鋁合金的方式得到，但采用纖維增強復合材料成型的網格結構能實現減重20%以上，同時，網格加強筋交錯的節點處可以增強整體結構的阻尼特性，具有良好的抗沖擊性能[6–7]。

網格加強結構的成型方式有多種，包括纏繞、鋪放、編織、互鎖工藝、真空輔助樹脂傳遞模塑等十余種。其中，具有規則回轉體形狀的網格構件，其纏繞成型有明顯的優勢：技術成熟、自動化程度高、效率高、纖維連續等。網格構件大多采用干法纏繞，其原理是將纖維預浸絲/帶，按照網格軌跡纏繞到網格芯模上，并增至規定的厚度，隨后進行固化脫模，形成網格加強結構。然而網格構件結構尺寸較多，且參數之間相互耦合，同時結構參數對網格結構整體力學性能的影響尚未明確，限制了其在航空航天領域上的應用，因此，對網格構件進行結構設計優化，以確定適宜的結構參數，是滿足網格結構強度及可靠性的重要前期保障[8]。

現階段，國內外學者對網格纏繞構件已經開展了一定的基礎性研究工作。Belardi等[9]對受到不同外載的圓柱形網格構件進行了結構分析及參數優化，采用有限元法，計算網格結構的臨界屈曲荷載，探究了屈曲破壞模式，最后基于遺傳算法對結構進行了參數優化，減少了結構的整體質量。Yazdani等[10]研究了在準靜態軸向載荷作用下的薄壁圓柱殼網格加強結構的屈曲行為，結果表明，較少的加強筋數量能夠提升結構強度。此外，在軸向載荷作用下，螺旋肋比環肋對屈曲性能的影響更為顯著。南京航空航天大學的Li等[11]為主網格加強筋和次網格加強筋加強結構設計，其中主加強筋更厚，有助于提升網格構件的整體抗彎剛度，而次加強筋則可以提升局部的抗彎剛度。哈爾濱工業大學的張鵬[12]提出利用螺旋肋和環向肋的數量表征網格密度，制定了新型網格纏繞成型工藝，提出多絲嘴纏繞方案，即螺旋肋與環肋同時纏繞，以減少網格交叉點架空與堆積等節點缺陷，并建立了多絲嘴網格纏繞的數學模型。

雖然網格結構纏繞技術已取得一定成果，但網格結構具有較強的可設計性，如何通過優化結構提升承載效率，尚未有充分的參數化理論模型。此外，網格結構參數較多，參數之間相互耦合，采用試驗試湊法優化結構成本較高、效率較低。為此，本文針對以上問題，以衛星Kagome網格承力筒為研究對象，開展結構優化研究。采用有限元方法，得到現有工況條件下網格承力筒的承載性能。通過參數化建模及加強筋獨立設計的思路，獲得各個結構參數對承載性能的影響；采用多目標遺傳算法，優化了結構參數，并對最優結構的強度、屈曲性能進行分析；最后，采用自主研制的桌面式纏繞機對網格承力筒進行了纏繞成型。

網格承力筒有限元模型及其邊界條件

1 網格承力筒有限元模型

網格承力筒主要由螺旋筋及環向筋兩個加強筋組成，由于加強筋結構長度方向上尺度遠大于截面方向，因此，可以采用三維梁結構等效加強筋結構。本文利用Ansys軟件，通過梁單元BEAM189劃分承力筒的有限元模型，并對網格承力筒的整體承載性能進行分析及評價。

網格承力筒所用預浸料為M40J環氧樹脂預浸料，該預浸料的材料基本屬性包括：纖維向楊氏模量Ex=220GPa、垂直纖維向楊氏模量Ey=Ez=7GPa、泊松比νxy=νxz=0.32、νyz= 0.3、剪切模量Gxy=Gxz=6.8GPa、Gyz=6.7GPa、材料密度為1.7g/cm3。網格承力筒的初始幾何參數如表1所示。

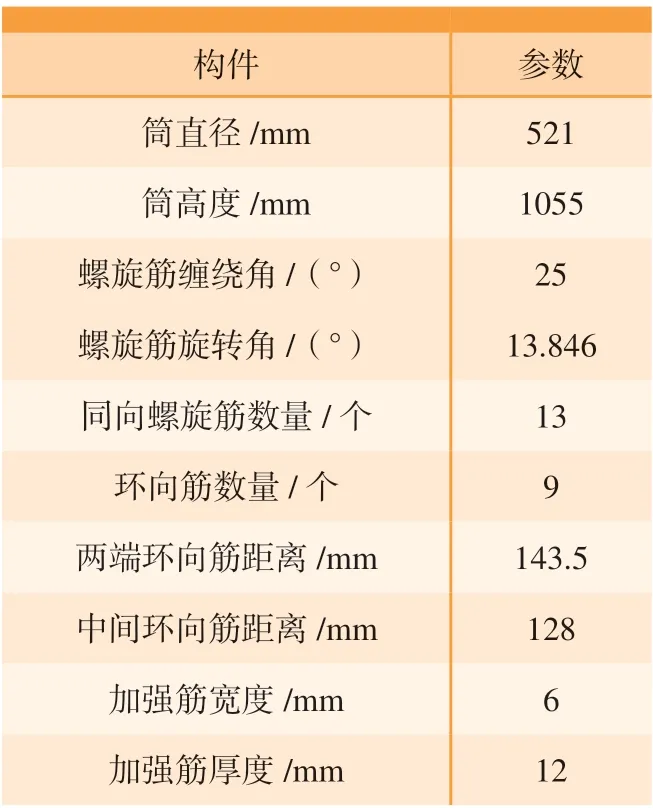
表1 網格承力筒的初始幾何參數Table 1 Initial geometric parameters of grid cylinder

有限元建模時將兩條旋向相反的螺旋筋定義為一對螺旋筋，螺旋起點相交定義為初始狀態。螺旋筋繞承力筒軸線方向的旋轉角度定義為螺旋筋的旋轉角。該角度不僅能夠確定螺旋筋的位置，還能確定螺旋筋與環筋相交節點的相對位置。根據上述承力筒幾何尺寸及網格劃分定義的有限元模型如圖1（a）所示。根據實際工況條件定義網格承力筒結構有限元模型的邊界及承載條件，承力筒底部采用固支約束，并約束前端面的徑向位移。根據衛星承力筒的實際工況條件，在前端面利用均布形式施加壓縮載荷和水平剪切載荷，如圖1 （b）所示。Fx為水平剪切載荷；Fy為軸向壓縮載荷。由于前端面環筋各位置的彎矩大小不同，因而各網格具有不同的軸向位移。在螺旋筋和環筋交叉節點附近彎矩最小，環筋變形也較小，但螺旋筋交叉的節點位移較大，這不符合實際軸向壓縮試驗的變形情況。為了保證模型的準確性，邊界條件施加時耦合了前端面單元的軸向位移，使前端面環筋在壓縮過程中保持相同的軸向位移。

圖1 網格承力筒有限元模型及邊界條件的施加Fig.1 Finite element model and boundary conditions of the grid cylinder

2 承載性能分析

根據網格承力筒的有限元模型及邊界條件，分析水平剪切載荷Fx在300kN、軸向壓縮載荷Fy在60kN的受力下整體變形及應變情況，如圖2所示。

由圖2（a）可知，該工況下承力筒發生軸向位移及水平位移，最大變形量為2.89mm。由圖2（b）可知，由于螺旋筋主要承受軸向壓縮載荷的作用，環筋主要承受水平剪切載荷的作用，因此，螺旋筋內部以壓應力為主，環筋以拉應力為主。由于受到該工況載荷的共同作用，導致上半側左螺旋筋的壓應力大于右螺旋筋，下半側則相反。應力最大值在下半側右螺旋筋處，為735.26MPa。對于環筋的拉應力的規律基本與螺旋筋一致，即上半側左環筋拉應力比右環筋大，下半側反之，最大值在上半側第2環筋左側，為302.01MPa。由圖2（c）可知，切應力在承力筒左上部及右下部較大，其中最大值在右下部的螺旋筋及下端面環筋交叉節點處，為367.63MPa。綜上所述，雖然壓縮載荷比水平剪切載荷小，但筋條的壓應力明顯高于其他方向應力，說明該種工況下，筋條應力以壓應力為主。

圖2 網格承力筒在特定工況下的變形及應力場分布Fig.2 Deformation and stress distribution of grid cylinder under specific working condition

網格承力筒結構參數對承載性能的影響

1 網格承力筒參數化幾何模型

本部分采用Ansys參數化建模方法，網格承力筒構件的有限元模型，其中重要的參數包括：承力筒直徑D、承力筒高度H、承力筒螺旋角A、同向螺旋筋數量M、螺旋筋旋轉角度P、環向筋距離（H2～H8）、加強筋厚度T與寬度W，網格承力筒幾何模型如圖3所示。

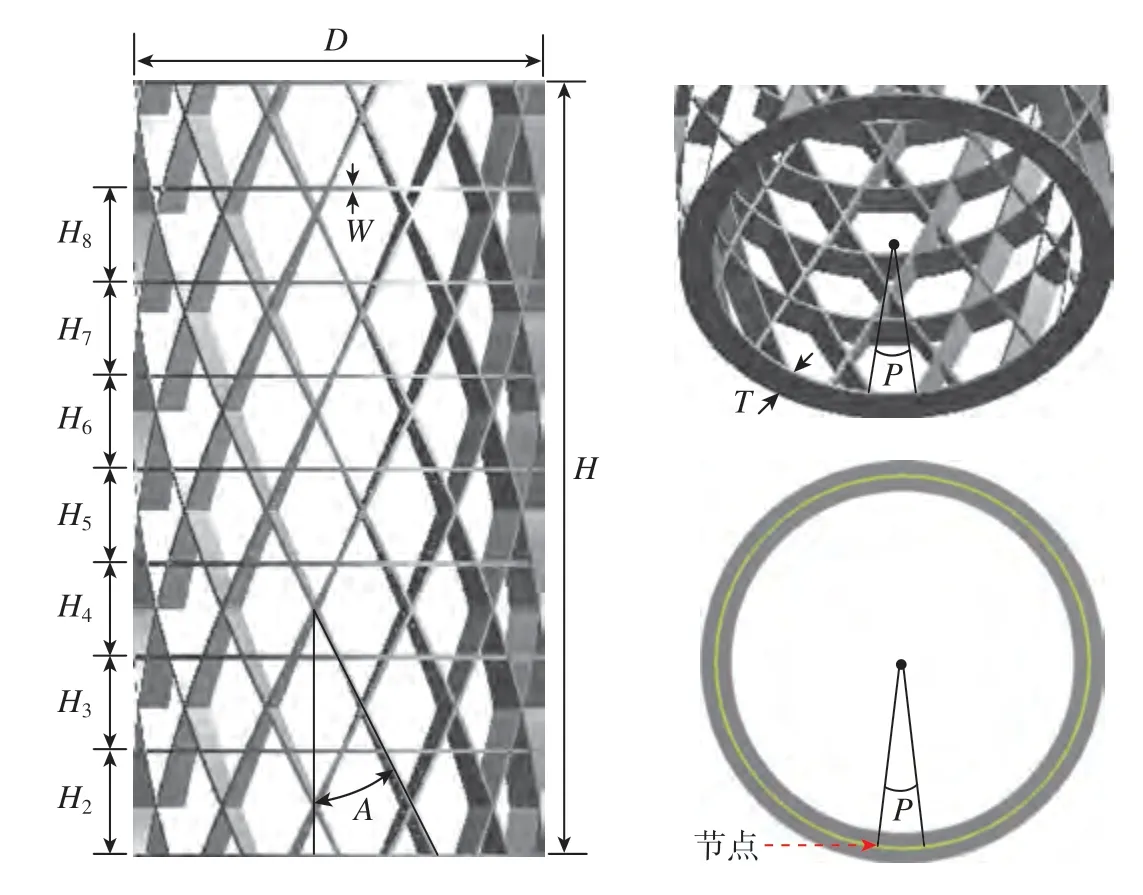
圖3 網格承力筒幾何模型Fig.3 Geometric model and parameters of the grid cylinder

為了減少螺旋筋與環筋結構參數之間的耦合作用，本部分提出結構的并行設計概念，將螺旋筋和環筋的結構設計相對獨立，從而避免兩種結構設計的相互干涉和不符合使用工況的情形。由前文分析可知，筋條應力以壓應力為主，在此工況下，承力筒最可能首先發生的是壓縮失效。因此，本部分以筋條最大壓應變與整體質量的比值來表征承力筒的承載效率，用承載效率系數Q表示。單位質量的應變越小，Q值越小，承載效率越高。網格承力筒的質量m可由式（1）得出：

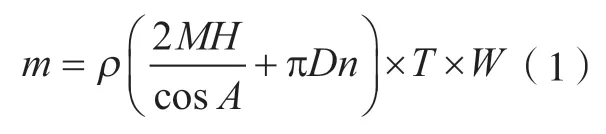
其中，ρ為網格承力筒密度；n為環筋數量。

2 螺旋角對結構承載性能的影響

參照表1，保持其他幾何參數不變，螺旋角設置范圍為[0°，60°]。從承力筒的質量來講，螺旋角為0°時，質量最小，原因是所用螺旋筋長度最短，螺旋角為60°時質量最大。根據式（1）計算，螺旋角在約束范圍內，承力筒質量在18kg至30kg之間。螺旋角A對最大壓應變、拉應變、剪切應變、質量承載效率系數Q的影響規律，如圖4所示。

由圖4可知，螺旋角對各承載性能參數的影響規律基本一致，均隨著螺旋角的增加呈現先極速下降后緩慢上升的趨勢。螺旋角在15°～20°時，筋條最大壓應變、筋條拉應變、剪切應變值最小，且承載效率系數最低，說明螺旋角在此區間內，承力筒承載效率最高。此外，螺旋角在0°～10°時，承載效率降低速率最快，此時剪切應變占主導地位，較小的螺旋角承載剪切載荷能力較弱，且無螺旋角時完全無法承受剪切載荷，因此，承載能力下降較快。而雖然較大的螺旋角承載壓縮載荷的能力弱，但設定的最大螺旋角為60°，一定程度上也能承受一些壓縮載荷，因此，曲線后期會緩慢上升。綜上所述，網格結構承載能力與螺旋角關系密切，可見螺旋角是網格結構的重要設計參數之一。

圖4 螺旋角對結構承載性能的影響Fig.4 Effect of helix angle on load-bearing performance

3 螺旋筋旋轉角對結構承載性能的影響

保持其他幾何參數不變，詳見表1，探究螺旋筋旋轉角P對結構承載性能的影響規律。由圖1可知，螺旋筋旋轉角不同，環筋和螺旋筋之間的交叉節點位置會發生改變，從而影響結構整體力學性能。設定螺旋筋旋轉角P取值范圍為[0°，60°]，設計點為60個。由于螺旋筋旋轉角P對結構質量的影響不大，因此，螺旋筋旋轉角P與承載效率關聯性較小。本部分主要探究螺旋筋旋轉角P對承力筒筋條最大壓應變、軸向位移及軸向剛度的影響，如圖5所示。

由于同向螺旋筋數量為13，因而螺旋筋旋轉角每過27.69°為一個周期，螺旋筋旋轉角在0°～60°范圍內應循環約2.2個周期。由圖5所示，周期性變化與計算基本一致，從壓應變變化趨勢中發現，在單個周期中呈現上升–下降–再上升–再下降的變化特征。其原因是當螺旋筋旋轉角較小時，不同旋向的螺旋筋下端部距離較近，最大壓應變發生在下端部螺旋筋與環筋的交叉節點處，隨著螺旋筋旋轉角增加，最大壓應變值降低，直到螺旋筋旋轉角增加到5°左右時，不同旋向的螺旋筋上端部距離較近，此時最大壓應變的位置發生變化，在上端部螺旋筋與環筋的交叉節點處，隨著螺旋筋旋轉角繼續增加，最大壓應變值降低。螺旋筋旋轉角對軸向位移及軸向剛度的影響規律基本一致，呈現先上升后降低的趨勢，其中螺旋筋旋轉角在約23°時，軸向位移出現最小值約1.185mm，軸向剛度出現最大值約2.535×105N/m。

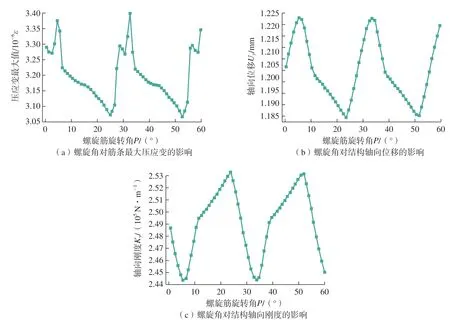
圖5 螺旋筋旋轉角對結構承載性能的影響Fig.5 Effect of rotation angle on load-bearing performance

4 筋條形狀對結構承載性能的影響

本部分主要探究筋條寬度及厚度等形狀特征對結構承載性能的影響。在其他結構參數不變的情況下，分別設定筋條寬度及厚度的變化范圍為[2mm，20mm]，均勻選取范圍內的10個設計點。由式（1）計算出不同筋條形狀參數對承力筒質量的影響，發現筋條寬度及厚度對承力筒質量均呈現線性正相關關系，而筋條最大壓應變呈負相關關系，如圖6所示，可知筋條寬度及厚度的增加可以提升軸向剛度。

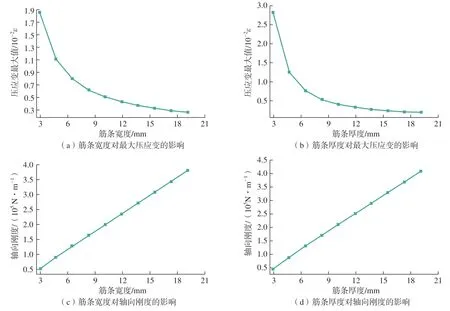
圖6 筋條形狀對結構承載性能的影響Fig.6 Effect of rib shape on load-bearing performance

從圖6可以看出，隨著筋條厚度的增加，結構最大壓應變下降速率較快，由此得知，筋條厚度對承載性能的影響會更大。通過對結構件的軸向剛度分析發現，筋條寬度和厚度均與軸向剛度呈線性正相關關系，但筋條厚度對軸向剛度的關系斜率明顯大于筋條寬度，因此說明筋條厚度對軸向剛度的影響也較寬度顯著。

網格承力筒結構參數優化及工藝實現

1 基于多目標遺傳算法的結構參數優化

基于以上仿真分析及幾何參數與承載性能的關系分析，對網格承力筒進行結構參數優化。由于多目標遺傳算法（Multi-objective genetic algorithm, MOGA）具有響應速度快、不需要訓練、可以處理離散變量等優勢，適合網格承力筒結構參數優化的計算。網格承力筒結構參數優化流程包括：設計變量選擇、約束條件確定、目標函數的確定、優化計算及結果分析等。設計變量包括螺旋角A、螺旋筋旋轉角P、環筋間距（H2～H8）、筋條寬度W及筋條厚度T。約束條件的確定可依據幾何參數與承載性能的關系，如表2所示。

表2 網格承力筒幾何參數的約束條件Table 2 Constraint conditions of cylinder geometric parameters

網格承力筒在承載力學最優條件下，尋求最小的質量，故將承力筒質量同時作為目標函數。網格承力筒結構參數優化流程，如圖7所示。

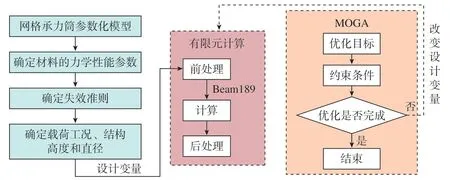
圖7 網格承力筒結構參數優化流程Fig.7 Optimization process of cylinder structural parameters

通過多目標遺傳算法，獲得網格承力筒結構的最優結構參數：螺旋筋纏繞角A為16.625°；螺旋筋旋轉角P為17.172°；兩端環筋間距H2為129.48mm；中間環筋間距H3～H8分別為129.11mm、115.30mm、119.60mm、127.87mm、 132.91mm和127.53mm。經仿真分析驗證發現，該最優工藝參數的最大壓應變為3715.8με，最大壓應變為1361.2με，最大切應變為3715.9με，不會發生強度失效。優化后結構整體質量為4.423kg，比初始方案降低了約21.2%。

2 優化后結構的屈曲性能分析

網格承力筒的屈曲失效也是其典型失效形式之一，而屈曲失效往往早于強度失效。經過上一部分的論證發現，在現有約束條件下，優化后的網格承力筒不會發生強度失效。為了進一步驗證優化后網格承力筒在現有約束下的屈曲性能，對其進行線性屈曲分析，如圖8所示。

圖8 網格承力筒屈曲模態分析Fig.8 Buckling modal analysis of grid cylinder

由圖8可知，網格承力筒X向兩側的螺旋筋屈曲模態振型較大，原因是承力筒上端面受到兩種方向載荷的共同作用導致的。網格承力筒一階屈曲系數為1.774，二階屈曲系數為1.794，均大于行業抗傾覆標準穩定系數1.5，可見優化后的網格承力筒在現有約束條件下不會發生屈曲失效。

3 網格結構的成型

哈爾濱工業大學數控纏繞機研究所在前期研究的基礎上，針對小型回轉結構件、衛星網格構件等應用目標，研發出了一套桌面開放式纏繞機控制系統，如圖9所示。通過優化后的網格承力筒參數，利用桌面式纏繞機，完成了樣件纏繞成型。

圖9 自主研發的小型桌面式纏繞機Fig.9 Self-developed of small desktop winding machine

結論

（1）本文采用參數化建模方法，提出網格承力筒環筋與螺旋筋獨立設計的思想，減少了兩種加強筋之間的耦合作用，使網格承力筒結構設計更為靈活、可控。

（2）在現有工況下，筋條應力以壓應力為主。承載性能隨著螺旋角的增加呈現先極速下降后緩慢上升的趨勢。螺旋角在15°～20°時，筋條最大壓應變、筋條拉應變、剪切應變值最小，承力筒承載效率最高。

（3）壓應變分析發現，螺旋筋旋轉角在單個周期中呈現上升–下降–再上升–再下降的變化特征，最大壓應變值在單個周期中不斷變化。軸向位移及軸向剛度隨螺旋筋旋轉角變化呈現先上升后降低的趨勢，其中螺旋筋旋轉角在約23°時，軸向位移最小，軸向剛度最大。

（4）隨著筋條寬度及厚度的增加，最大壓應變呈下降趨勢。相較于筋條寬度，筋條厚度對承載性能的影響會更大。

（5）優化后的網格承力筒結構，螺旋筋纏繞角A為16.625°、螺旋筋旋轉角P為17.172°、兩端環筋間距H2為129.48mm、中間環筋間距H3～H8分別為129.11mm、115.30mm、119.60mm、127.87mm、132.91mm和127.53mm。優化后網格承力筒質量比初始方案降低了約21.2%，且不會發生強度失效及屈曲失效。