數學圖形在高中數學教學中的重要性

張國蘭 沈興斌

【摘要】高考是學生重要的轉折點，其不僅代表著學生寒窗苦讀的階段性結束，同時也是對學生綜合能力和素質的一次考查.而圖形在高中數學教學中發揮著不可小覷的影響和作用，教師既可以通過圖形幫助學生分析教學中案例，加深學生對數學知識理解，又可以利用圖形豐富數學學習內容，緩解學生在數學學習過程中的枯燥和乏味，進而幫助學生提高數學成績，提升教學效果.

【關鍵詞】數學圖形;高中;數學教學;重要性

引言

眾所周知，數學知識會伴隨著學生年級的遞增出現學習難度加大的現象.而數學作為高中階段較為重要的一門學科，同時也是讓學生和老師最為“頭痛”科目之一，其主要是由幾何知識和代數知識兩大部分構成，這兩部分均需要數學圖形的參與.教師應該充分利用數學圖形處理抽象及難度較高的數學知識，降低學生的學習難度，提升其自信心和對于高中數學知識的學習興趣，從而整體提高我校數學教師的教學水平和學生的學習成績.

一、數學圖形的概念

數學圖形指的是與數學知識有關的圖形，通常由點、線、面及相關形狀結構構成，例如：幾何圖形，函數圖形等，其中包括簡單的平面圖形（直線、曲線、多邊形、平面區域等）和空間圖形（空間曲線、曲面、空間區域等）以及由數學軟件、計算機和計算器繪制的圖形（分形圖形、微分方程的解曲線等）.數學圖形可以有效幫助學生理解教材中的案例分析，拓展其解題思路，可以幫助教師在數學教學過程中進行知識點的梳理和引導，同時有助于教師簡化教學過程，提高整體教學效果.

二、數學圖形在高中數學教學中的重要性

（一）拓展高中生的思維

在高中數學教學過程中，教師可以利用數學圖形對相關數學知識、問題進行詳細的解析，并幫助學生拓展解題思路，整體提升學生對于高中數學知識的理解能力以及解題效率，鍛煉學生的思維能力，使其在不斷地自主發問和解答中提升自己的綜合能力，同時為難度較大的高中數學題提供辨析思路、奠定一定的基礎.例如，在講解例題1時，教師可以利用數學圖形在等腰梯形ABCD內作垂直線，并求出AD2、AE、CD的值，之后根據等腰梯形的相關特性得出方程組：x>0，x2r>0，2r-x2r>0，計算并得出結果.教師通過圖形不僅幫助學生回顧了等腰梯形、直角等相關數學基礎知識，還借助半圓形題目拓展了學生的思路，最終以函數方程作為解題的最后環節，讓學生知道對于相關題型可以采用該種思路進行解答.

例1一個半圓形木塊，其半徑為r，要求截取后的圖形為一個等腰梯形，而等腰梯形ABCD中的C、D點分別處于半圓形木塊的圓周上，AB為半圓形木塊的直徑，求等腰梯形ABCD周長及腰長的函數關系，并求出其定義域.

解設等腰梯形ABCD周長為y，腰長為x，由對稱性得出：CD=AB-2AE，所以AE=AB-CD2，作DE垂直與AB，其中E為垂足.

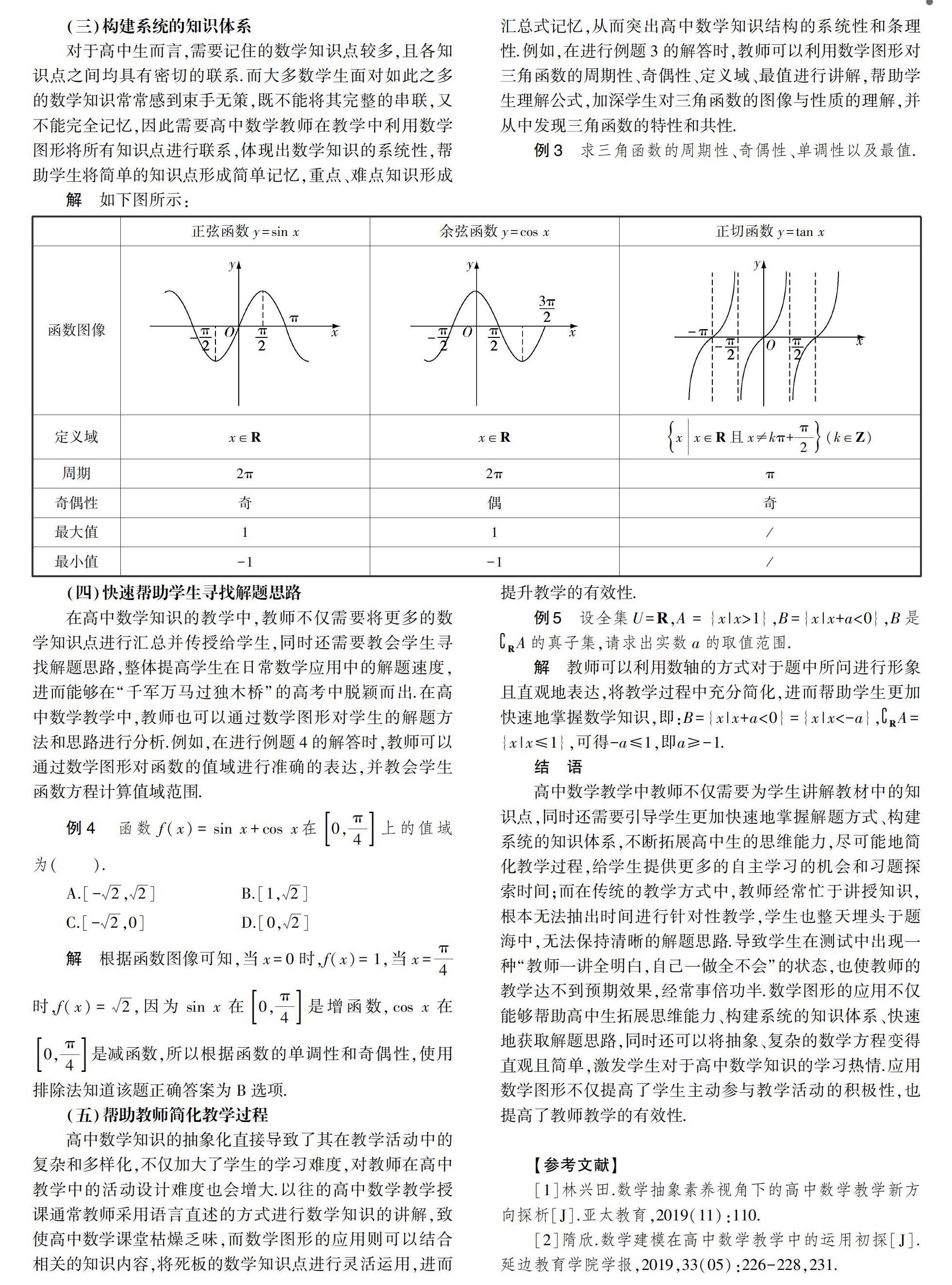
此時連接BD，得出∠ADB=90°，所以Rt△ADE∽Rt△ABD，AD2=AE×AB，AE=x22r，所以CD=AB-2AE=2r-x2r，得出等腰梯形ABCD周長y=2r+2x+2r-x2r=-x2r+2x+4r.又因為ABCD為圓內梯形，所以AD>0，AE>0，CD>0，即得出：x>0，x2r>0，2r-x2r>0，一組方程式，最終得出0

（二）將數學知識具體化和形象化

高中數學知識相對比較抽象，導致學生的學習難度加大，喪失一定的學習興趣.而教師在高中數學教學過程中則需要利用數學圖形將抽象的數學知識具體化和形象化，從而降低學生的學習難度，提升學生的學習興趣和最終學習質量.教師可以靈活地運用數學圖形對相關數學知識和問題進行解答，并通過反復的驗證使學生了解和重視高中數學知識和圖形之間的相關性，使學生在自我認知里降低高中數學知識的難度.例如，在進行例題2的解答時，教師可以利用數學圖形將函數解析式進行分解及合并，將抽象的分段函數形象化，可以幫助學生對函數解析式進行更好的理解，還可以幫助教師更形象化地講解函數解析式和分析例題，進而整體提升高中數學教學的效果.

例2出租車屬于人們日常出行中常用的一種交通工具.某城市圖2的出租車行程計費規則如下，如果出行行程在3千米以內，則按起步價收取7元，如果出行行程超過3千米，超出路程部分為每千米收取2.4元，求收費與路程二者關系函數解析式.

解設某個人出行路程為x千米，總收費為y元，能夠得出圖像（圖2），所以有y=7，03，得出y=7，0

2.4x-0.2，x>3

（三）構建系統的知識體系

對于高中生而言，需要記住的數學知識點較多，且各知識點之間均具有密切的聯系.而大多數學生面對如此之多的數學知識常常感到束手無策，既不能將其完整的串聯，又不能完全記憶，因此需要高中數學教師在教學中利用數學圖形將所有知識點進行聯系，體現出數學知識的系統性，幫助學生將簡單的知識點形成簡單記憶，重點、難點知識形成匯總式記憶，從而突出高中數學知識結構的系統性和條理性.例如，在進行例題3的解答時，教師可以利用數學圖形對三角函數的周期性、奇偶性、定義域、最值進行講解，幫助學生理解公式，加深學生對三角函數的圖像與性質的理解，并從中發現三角函數的特性和共性.

例3求三角函數的周期性、奇偶性、單調性以及最值.

解如下圖所示：

正弦函數y=sin x余弦函數y=cos x正切函數y=tan x

函數圖像

定義域x∈Rx∈Rxx∈R且x≠kπ+π2（k∈Z）

周期2π2ππ

奇偶性奇偶奇最大值11/

最小值-1-1/

（四）快速幫助學生尋找解題思路

在高中數學知識的教學中，教師不僅需要將更多的數學知識點進行匯總并傳授給學生，同時還需要教會學生尋找解題思路，整體提高學生在日常數學應用中的解題速度，進而能夠在“千軍萬馬過獨木橋”的高考中脫穎而出.在高中數學教學中，教師也可以通過數學圖形對學生的解題方法和思路進行分析.例如，在進行例題4的解答時，教師可以通過數學圖形對函數的值域進行準確的表達，并教會學生函數方程計算值域范圍.

例4函數f（x）=sin x+cos x在0，π4上的值域為（）.

A.[-2，2]B.[1，2]

C.[-2，0]

D.[0，2]

解根據函數圖像可知，當x=0時，f（x）=1，當x=π4時，f（x）=2，因為sin x在0，π4是增函數，cos x在0，π4是減函數，所以根據函數的單調性和奇偶性，使用排除法知道該題正確答案為B選項.

（五）幫助教師簡化教學過程

高中數學知識的抽象化直接導致了其在教學活動中的復雜和多樣化，不僅加大了學生的學習難度，對教師在高中教學中的活動設計難度也會增大.以往的高中數學教學授課通常教師采用語言直述的方式進行數學知識的講解，致使高中數學課堂枯燥乏味，而數學圖形的應用則可以結合相關的知識內容，將死板的數學知識點進行靈活運用，進而提升教學的有效性.

例5設全集U=R，A = {x|x>1}，B={x|x+a<0}，B是瘙綂RA的真子集，請求出實數a的取值范圍.

解教師可以利用數軸的方式對于題中所問進行形象且直觀地表達，將教學過程中充分簡化，進而幫助學生更加快速地掌握數學知識，即：B={x|x+a<0}={x|x<-a}，瘙綂RA={x|x≤1}，可得-a≤1，即a≥-1.

結語

高中數學教學中教師不僅需要為學生講解教材中的知識點，同時還需要引導學生更加快速地掌握解題方式、構建系統的知識體系，不斷拓展高中生的思維能力，盡可能地簡化教學過程，給學生提供更多的自主學習的機會和習題探索時間;而在傳統的教學方式中，教師經常忙于講授知識，根本無法抽出時間進行針對性教學，學生也整天埋頭于題海中，無法保持清晰的解題思路.導致學生在測試中出現一種“教師一講全明白，自己一做全不會”的狀態，也使教師的教學達不到預期效果，經常事倍功半.數學圖形的應用不僅能夠幫助高中生拓展思維能力、構建系統的知識體系、快速地獲取解題思路，同時還可以將抽象、復雜的數學方程變得直觀且簡單，激發學生對于高中數學知識的學習熱情.應用數學圖形不僅提高了學生主動參與教學活動的積極性，也提高了教師教學的有效性.

【參考文獻】

[1]林興田.數學抽象素養視角下的高中數學教學新方向探析[J].亞太教育，2019（11）：110.

[2]隋欣.數學建模在高中數學教學中的運用初探[J].延邊教育學院學報，2019，33（05）：226-228，231.