基于ArcGIS的西寧市城區地質災害危險性分區評價

范吉新，趙啟飛，王靖天，王萬鑫，李衛柯

(1.青海煤田地質局，青海 西寧 810012；2.西安科技大學 地質與環境學院，陜西 西安 710054)

西寧市位于青藏高原的東北部，是青藏高原與黃土高原的過渡地帶，整個地形南高北低，南至祁連山支脈拉雞山，北達湟水河谷地，屬于典型的山間河谷型城市并且也是我國海拔最高的城市之一，由于其脆弱的地質環境，使之成為我國受地質災害侵擾最為嚴重的城市之一[1，2]。近年來，因人類工程活動引發的生態環境惡化及地質災害頻發，使其區域內地質災害現象分布廣泛，尤其是滑坡、地面塌陷、地震等突發性的地質災害較為發育，對當地人民的人身安全、經濟活動等構成極其惡劣的影響[3]，因此，為了西寧市地質災害的防治和工程建設，對西寧市城區進行地質災害危險性分區刻不容緩[4]。

地質災害是由自然地質作用和人為工程活動造成的惡化地質環境，使原有的地質環境被破壞，平衡條件傾斜，導致地質體發生失穩的現象，它不僅屬于自然現象，還是社會經濟現象[5]。因此，在進行評價地質災害的危險性時，應綜合考慮影響地質災害發生的各種指標，并給這些指標賦予合適的權重系數，以便準確合理地區劃出地質災害低、中、高和極高危險性區。目前，國內張曉東等[6]利用層次分析法評估了鹽池縣地質災害的危險性；李雄峰等[7]采用層次分析法和可拓理論分區評價了水土流失的嚴重程度；李林漢等[8]將層次分析法運用于京津冀地區水資源承載能力評價；白建光等[9]將層次分析法與模糊綜合評判法結合分析了城市內澇生態治理。

1 評價方法

為了提高地質災害危險性評價的準確性，需要具體分析研究區的各種因素對地質災害的影響，選擇適宜的評價方法使得評價工作可行[10]。當前，對地質災害危險性分區評價的方法眾多，結合西寧市城區的地質環境背景以及地質災害發育特征等，在本次研究中采用層次分析法。此方法所需要的數據偏少，簡單快捷，是一種半定量的系統性分析方法，再綜合考慮遴選出的地質災害影響因子，保證了地質災害危險性分區評價的準確性。

層次分析法是由運籌學家Thomas Saaty提出的一種簡單靈活地將定量和定性分析結合的層次權重決策分析方法，具有很強的實用性，通過對研究區的總體把握，明確其基礎指標，將復雜的問題轉化為通過評價因子之間兩兩影響程度大小的比較，構造合理的判斷矩陣，求出矩陣的最大特征根及其特征向量，然后對矩陣的一致性做出驗證，最后將特征向量歸一化，便可得出每個評價因子相對應的權重值[11]。之后利用ArcGIS軟件構建各個評價因子的柵格圖層，結合已獲取的權重系數，通過空間分析中的柵格工具，進行多因子疊加分析，獲取西寧市城區地質災害危險性分區評價圖。

2 評價體系的建立

2.1 評價指標選取原則

地質災害的成因形形色色，是由眾多影響因素共同蘊育所產生的結果。地質災害發生的多樣性以及不確定性不僅表現在影響因素上，在不同的區域，各種影響因素對地質災害發生的貢獻程度也有很大差別，同一種評價方法適用于一個區域但不一定能夠成功評價另一個區域。因此，對于地質災害危險性評價選擇影響因子時，需要遵循5個原則：①評價因子的選取需要考慮獲取因子的難易程度，并且評價因子需具有代表性；②各影響因子之間要相互獨立，無關聯性，避免后期處理數據帶來不便；③不同的研究對象擁有不同的地質背景，需要準確選取占據主導地位的評價因子，提高評價結果的準確率；④評價因子的選取必須目的性明確，要求能夠充分的體現研究區域的危險性評價結果；⑤結合研究區域的空間效應選取評價指標將對評價體系產生重要影響[12]。

2.2 評價指標體系建立原則

由于地質災害發生的影響因素以及誘發條件是十分廣泛的，將所有的情況都考察在內無疑是不合理的，因此在構建評價體系的同時需要遵循3個原則：①所建立的評價體系需要能夠全面綜合系統地反映出最接近研究區域的真實情況；②應選擇對地質災害危險性評價影響較大的因素作為評價指標，適當去除一些間接因素，建立科學有效的評價體系；③由于不同評價區域的差異，有必要在充分考慮影響地質災害發生的主要因素的基礎上，對研究區域的地質構造和自然特征進行分析[13]。

2.3 危險性層次分析模型

依據層次分析法的基本原理，建立了如圖1所示的西寧市城區地質災害危險性評價因子層次分析模型。其中，地質災害危險性評價作為目標層A，而地質因素和誘發因素分別作為準則層B1和B2，指標層C作為影響地質災害發生的因子，如坡度C1、坡向C2、高程C3等[14]。

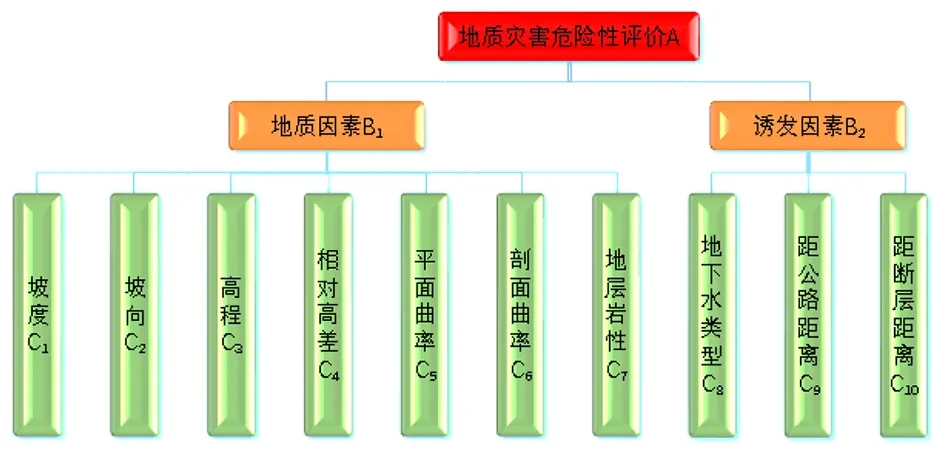
圖1 地質災害危險性評價因子層次分析模型

2.4 評價因子權重的確定

采用層次分析法計算各危險性因子的權重值，對照標度理論表，將各因子兩兩對比，得出所有因子相對重要性指數，從而構建判斷矩陣，標度理論表如表1所示。

表1 判斷矩陣標度理論

具體計算過程如下所示：

構造判斷矩陣：A=(aij)m×n，aij>0，

(1)

式中：aij為第i行j列因子重要性標度值。

歸一化處理判斷矩陣每一列元素：

(2)

處理后再按行相加：

(3)

對Wi進行歸一化處理：

(4)

所得近似特征向量W=(w1，w2，…，wn)T，就是各評價因子的權重[15]。

為了保證以上所得的權重系數的合理性，需對判斷矩陣進行一致性驗證，過程如下所示：

(5)

式中：λmax為判斷矩陣的最大特征根，n為判斷矩陣階數，CI表示判斷矩陣一致性指標。

(6)

式中：當CR<0.1時，則確定判斷矩陣具備良好的一致性，若CR>0.1，則需對判斷矩陣做出適當調整直至滿足條件；RI表示判斷矩陣平均隨機的一致性指標，其值由大量實驗給出，取值如表2所示。

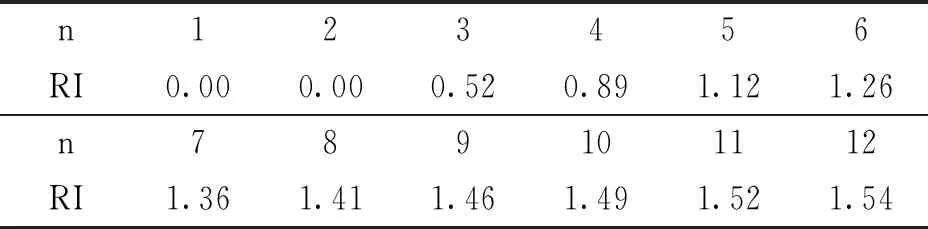
表2 平均隨機一致性指標RI

Bi構造準則層判斷矩陣如表3所示，計算求出最大特征根λmax=2，一致性指標CI=0，一致性比例CR=0<0.1，滿足要求。

表3 A-Bi判斷矩陣

B1-Ci構造地質因素判斷矩陣如表4所示，計算求出最大特征根λmax=7.365，一致性指標CI=0.061，一致性比例CR=0.045<0.1，滿足要求。

表4 B1-Ci判斷矩陣

B2-Ci構造誘發因素判斷矩陣如表5所示，計算求出最大特征根λmax=3.039，一致性指標CI=0.02，一致性比例CR=0.037<0.1，滿足要求。

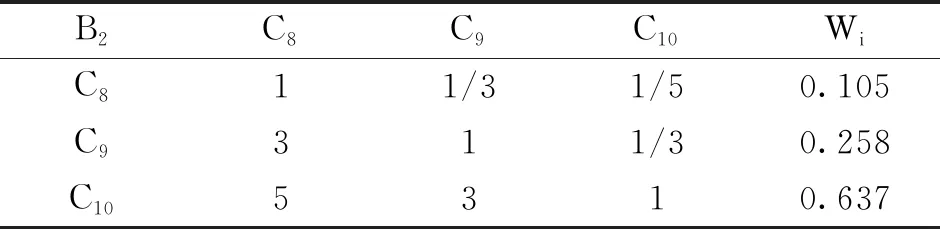
表5 B2-Ci判斷矩陣

由表3～表5可得知準則層和指標層中各影響因子的權重系數，而以上所求僅為一層因子對應于上一層因子的權重向量，要獲取指標層各個評價指標對于目標層的排序權重，就需要進行權重的合成計算[16]。方法如下所示：

(7)

式中：aj為評價指標的權重值。

求得CR=0.044<0.1，符合一致性原則，由此可知指標層的10個影響因子所取的權重系數均滿足要求。在表6中列出了所有地質災害危險性評價指標的權重值。

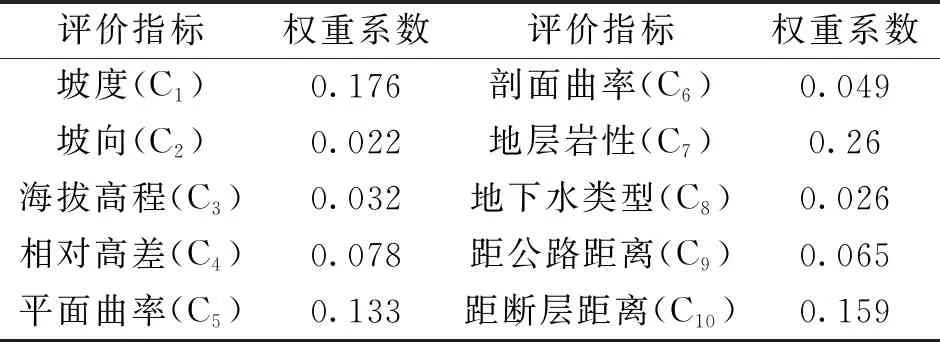
表6 評價指標權重系數

由表6可知，地層巖性對西寧市城區的地質災害危險性貢獻度最高，然后坡度、距斷層距離、平面曲率、相對高差、距公路距離、剖面曲率、海拔高程、地下水類型依次降低，坡向的權重值最低。

2.5 地質災害危險性區劃

依據建立的地質災害危險性評價數學模型，來達到對研究區的危險性區劃[17]，而西寧市城區地質災害危險性評價的數學模型基于層次分析法的綜合評價指數法，再通過ArcGIS 10.6的地圖代數工具，將各個評價指標的柵格圖層進行空間疊加運算，具體計算公式如下所示：

I=ΣWiCi

(8)

式中：I為第i個評價因子的危險性綜合指數，Wi為第i個評價因子的權重值，Ci為第i個評價因子的柵格圖層。根據表6中的數據，可以得知西寧市城區地質災害危險性評價數學模型為：

I=0.176C1+0.022C2+0.032C3+0.078C4+0.133C5+0.049C6+0.26C7+0.026C8+0.065C9+0.159C10

(9)

3 基于ArcGIS的地質災害危險性評價

本次研究采用的原始DEM數字高程模型精度為30m。由于柵格數據的像元屬性能充分反映該單元的空間分布位置，且利用ArcGIS可對研究單元進行全面管理，擁有計算簡捷、數據庫清晰、空間可視化、結果準確性高的優點[18]，因此將評價單元確定為柵格單元，大小為30m×30m。

3.1 海拔高程分區

利用ArcGIS 10.6將獲取的西寧市城區DEM原始數據處理成數字海拔高程模型。西寧市城區的地表海拔高程最高點為2 831m，最低點為2 118m，將地表高程按照(2118，2200)，(2200，2300)，(2300，2400)，(2400，2500)，(2500，2600)，(2600，2700)，(2700，2800)，(2800，2831)重分類為8個級別，得到的海拔高程單因素分區評價圖，如圖2所示。

圖2 海拔高程

3.2 地形相對高差分區

利用已獲取的DEM數據，通過ArcGIS 10.6中的焦點統計工具，生成西寧市城區的地形相對高差分布圖，可知其相對高差達到134 m。將其相對高差分布圖按照(0，20)，(20，50)，(50，90)，(90，134)重分類為4個類別，重分類之后的地形相對高差單因素分區評價圖，如圖3所示。

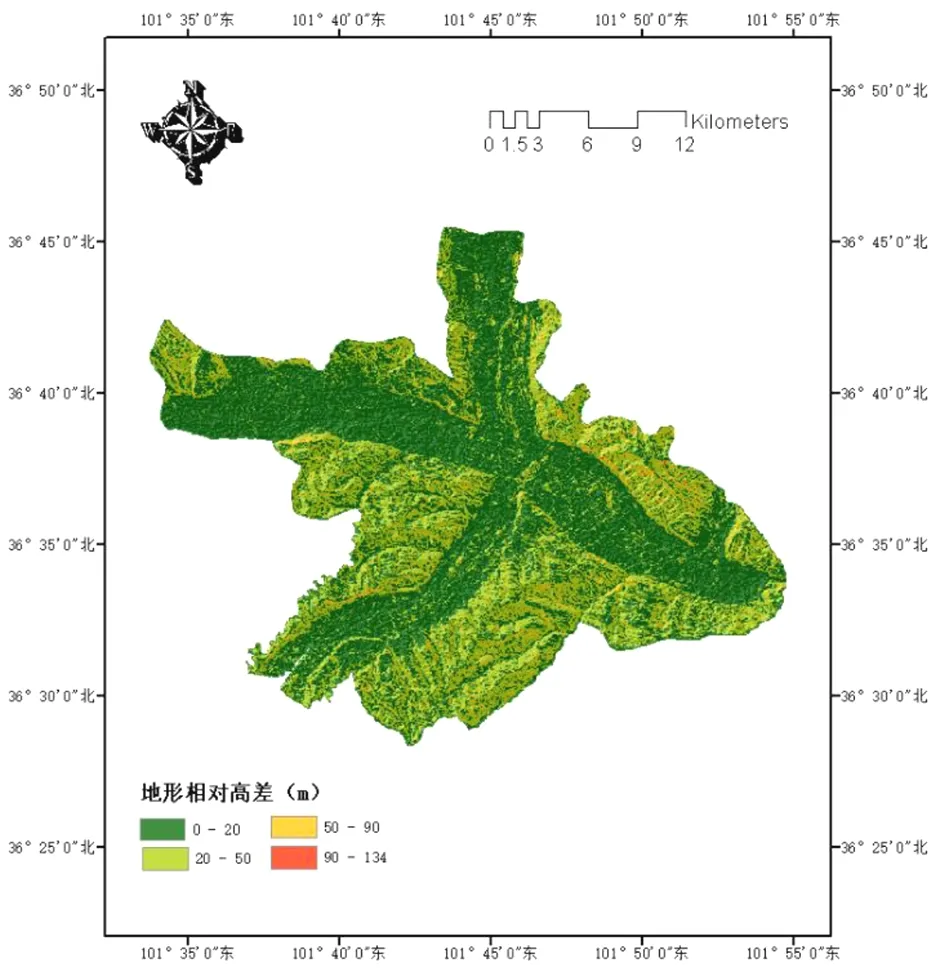
圖3 地形相對高差

3.3 地層巖性分區

利用ArcGIS 10.6從西寧市1∶50 000工程地質圖中矢量化出西寧市城區的主要地質巖土體類型，再依據工程地質圖中巖土體的分區情況，將其主要的巖土體類型重分為巖漿巖巖組、變質巖巖組、沉積巖巖組、卵礫類土、黏性土、雜填土及滑坡堆積物6類，轉為柵格圖層后，得到了西寧市城區地層巖性單因素分區評價圖，如圖4所示。

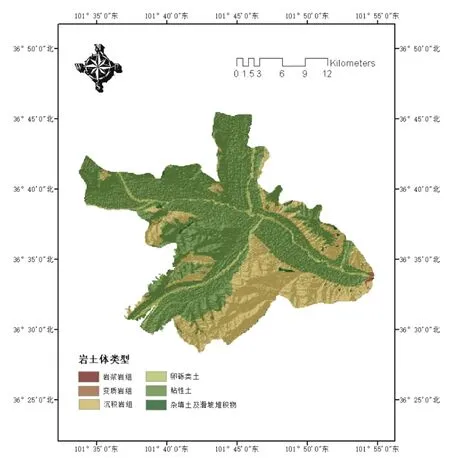
圖4 地層巖性

3.4 平面曲率分區

利用ArcGIS 10.6中表面分析的曲率工具，輸入原始DEM數據可獲取平面曲率分布圖，將其按照自然間斷法重分為(-6744086，-2040554)，(-2040554，-1283663)，(-1283663，-7430276)，(-7430276，-3105189)，(-3105189，1219898)，(1219898，5544986)，(5544986，1041071)，(1041071，1797961)，(1797961，7096193)9類，得到西寧市城區平面曲率單因素分區評價圖，如圖5所示。

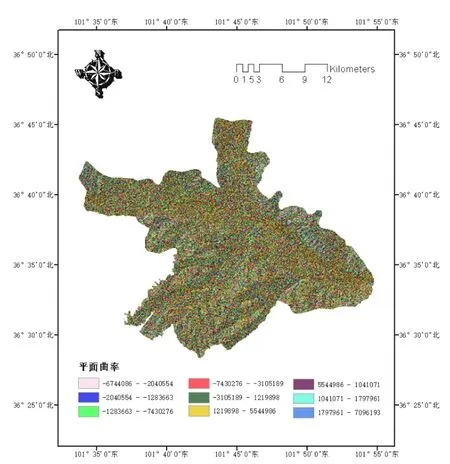
圖5 平面曲率

3.5 剖面曲率分區

通過ArcGIS 10.6中的曲率工具，計算出剖面曲率分布圖，再利用重分類工具，遵循自然間斷法重分為(-1104781，-2788088)，(-2788088，-1643177)，(-1643177，-9071624)，(-9071624，-3347066)，(-3347066，1559698)，(1559698，6466461)，(6466461，1382661)，(1382661，2527572)，(2527572，9887718)9類，即可獲取西寧市城區剖面曲率單因素分區評價圖，如圖6所示。

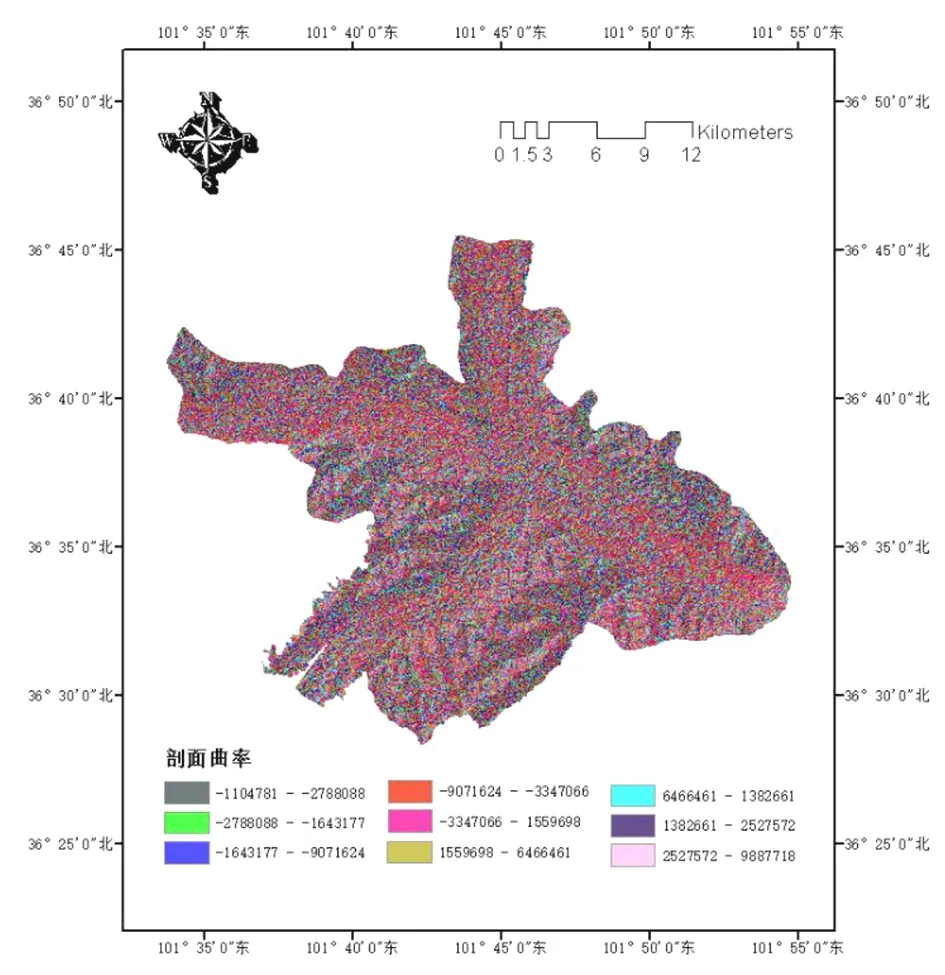
圖6 剖面曲率

3.6 距公路距離分區

從Google Earth上矢量化出西寧市城區的路網，導入ArcGIS中獲取路網分布圖，運用多環緩沖區工具進行路網的緩沖區分析，將距公路距離按照(0，100)，(100，200)，(200，300)，(300，400)，>400分為5類，重分類之后的西寧市城區距公路距離單因素分區評價圖，如圖7所示。

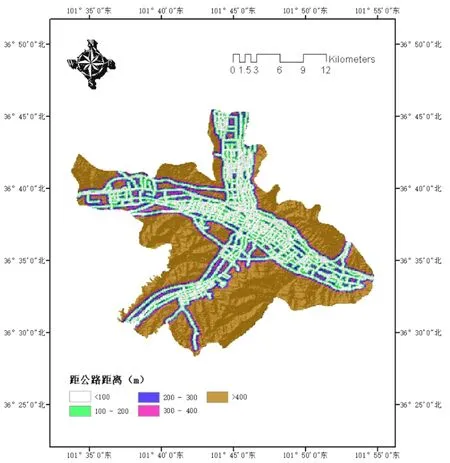
圖7 距公路距離

3.7 坡度分區

使用西寧市城區DEM數字高程模型，通過ArcGIS 10.6中3D Analyst的坡度工具，生成坡度分布圖。研究區內最大坡度達到60.9°，利用重分類中手動分類方式將其分成(0，10)，(10，20)，(20，30)，(30，40)，(40，50)，(50，60)，(60，70)7類，得到西寧市城區坡度單因素分區評價圖，如圖8所示。

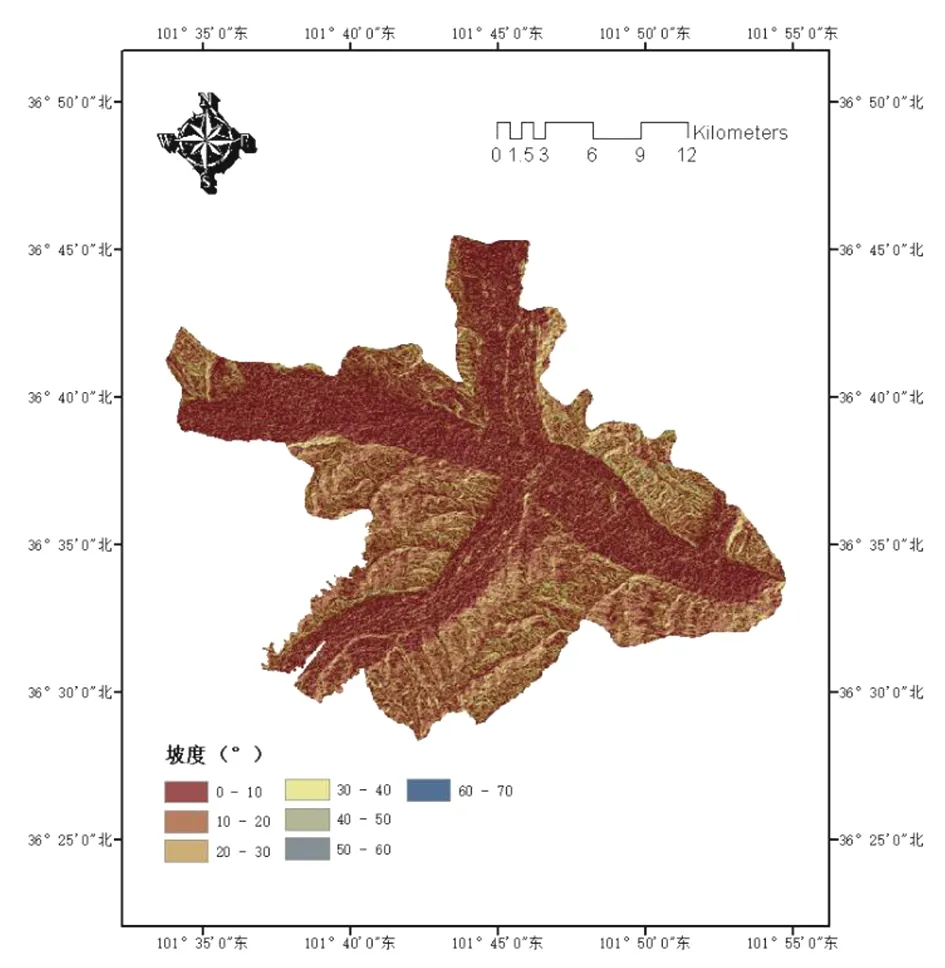
圖8 坡度

3.8 坡向分區

利用ArcGIS 10.6中的坡向工具，計算出研究區域的坡向單因素分區評價圖，如圖9所示。其中(-1)、(0，22.5)、(22.5，67.5)、(67.5，112.5)、(112.5，157.5)、(157.5，202.5)、(202.5，247.5)、(247.5，292.5)、(292.5，337.5)、(337.5，360)依次被區劃為平面、北面、東北面、東面、東南面、南面、西南面、西面、西北面、北面。

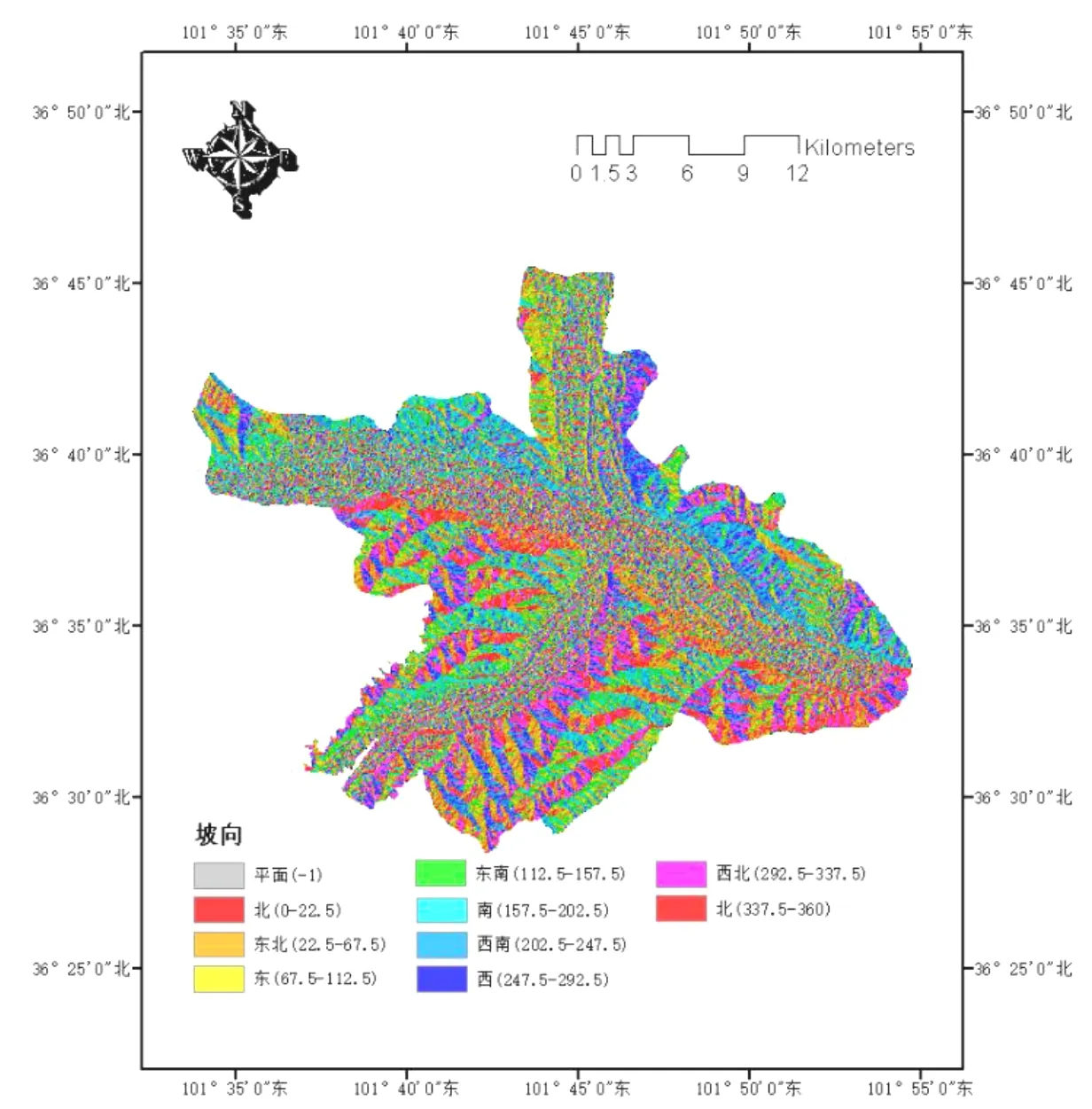
圖9 坡向

3.9 距斷裂構造距離分區

通過ArcGIS 10.6，從西寧市1∶50 000地貌及第四紀地質圖中矢量化提取出研究區域的主要斷裂構造，使用多環緩沖區工具對斷裂構造分布圖進行緩沖區分析，將距斷裂構造距離按照(0，300)，(300，600)，(600，900)，(900，1 200)，>1 200分為5類，生成的西寧市城區距斷裂構造距離單因素分區評價圖，如圖10所示。

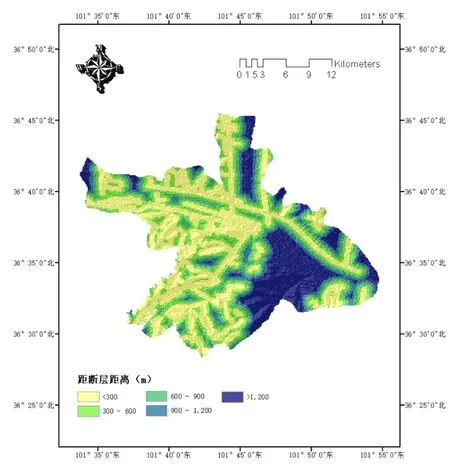
圖10 距斷裂構造距離

3.10 地下水類型分區

利用ArcGIS 10.6從西寧市1∶50 000水文地質圖中矢量化出研究區的主要地下水類型分布圖，參照水文地質圖中的區劃情況，將其劃分為松散巖類孔隙水、碎屑巖類裂隙孔隙水、碳酸鹽巖類巖溶裂隙水、基巖裂隙水4類，通過工具轉為柵格圖層后，得到西寧市城區地下水類型單因素分區評價圖，如圖11所示。

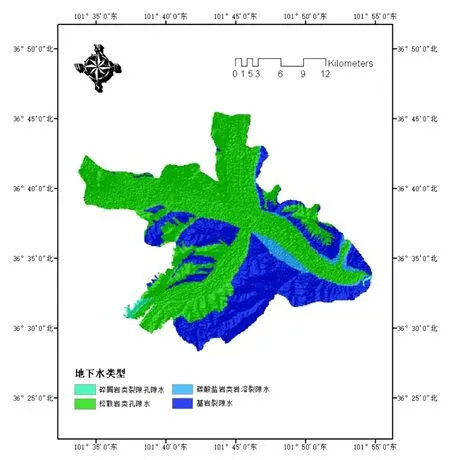
圖11 地下水類型

4 西寧市城區地質災害危險性評價結果

通過ArcGIS 10.6中的空間疊加分析技術，將已獲取的10個評價因子的單因素分區評價圖結合其相對應的權重系數分析得出西寧市城區地質災害危險性綜合分區評價圖，如圖12所示，由重分類中的自然間斷點分級法分類，將全研究區內的所有柵格按照地質災害危險性劃分為4個等級：低危險區、中危險區、高危險區、極高危險區[19]。自然間斷點分級方法是一種基于數據統計分布規律的分類統計方法，它可以最大程度地區分類別，識別分類間隔，并將相似的值劃分為最適宜的組[20]。

依據圖12可得知，西寧市城區地質災害危險性分區中，低危險區、中危險區、高危險區和極高危險區的面積分別占西寧市城區總面積的43%、19%、21%和17%，其餅狀分布圖如圖13所示，其中，極高危險性區主要位于西寧市城東區與城中區的八一路以南—曹家溝—小平兒嶺一帶，而高危險性區與中危險性區分布較為廣泛，并且分布在彼此周緣，主要位于西寧市城北區與城中區的下細溝村—泉爾灣村—沈家溝—海湖路以西區域，低危險性區主要分布在西寧市城北區與城中區的平坦地帶，大部分都屬于市區范圍。

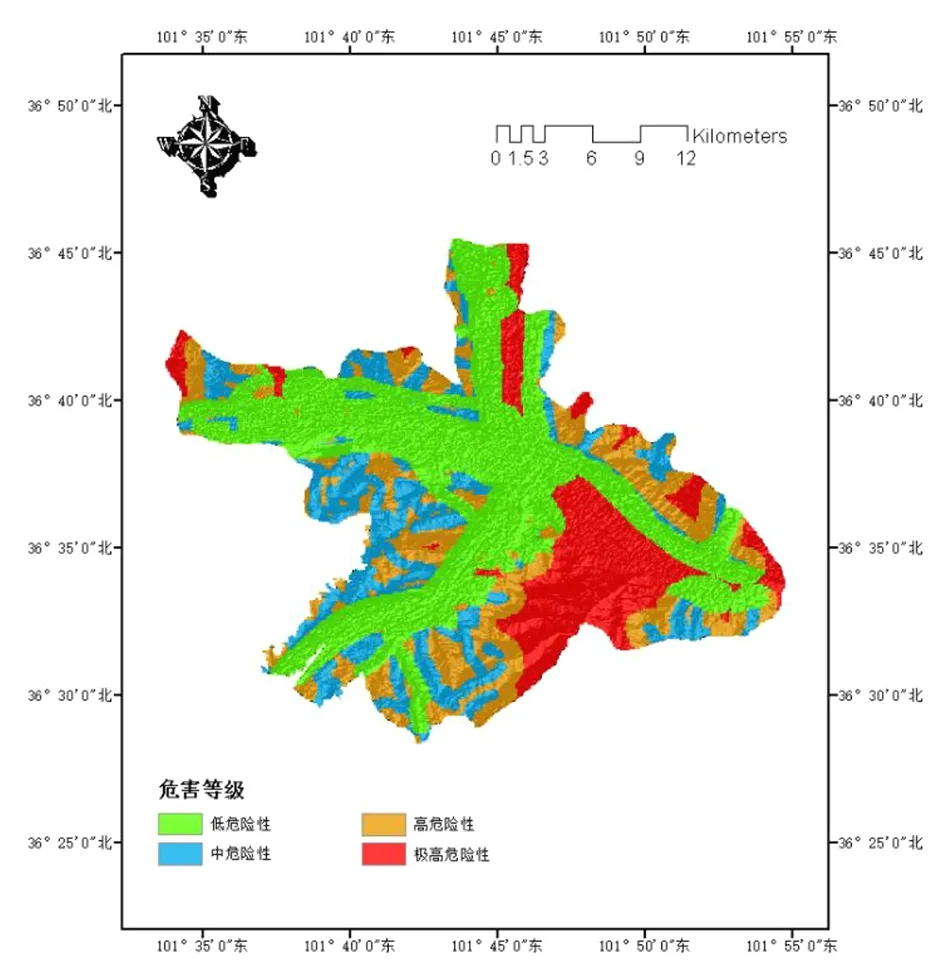
圖12 地質災害危險性分區評價

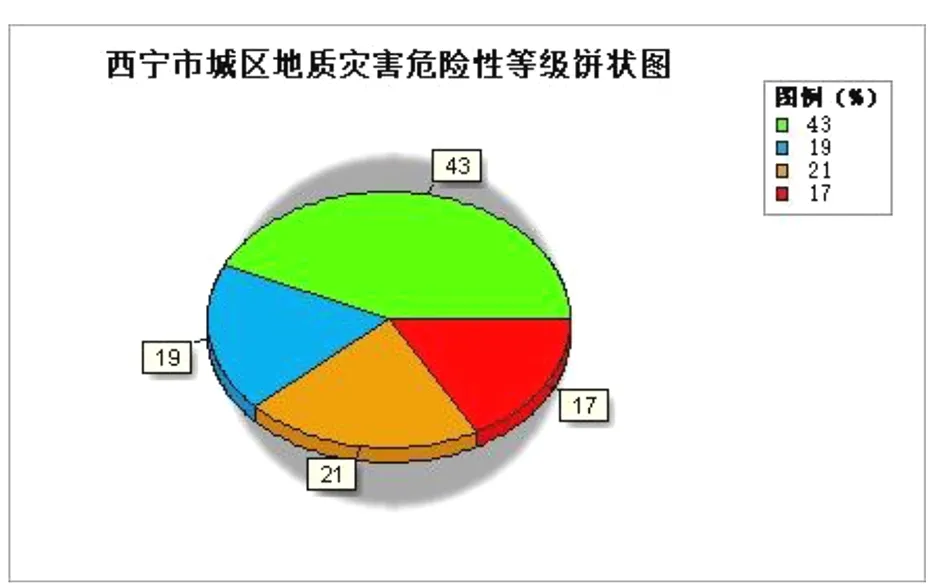
圖13 危險性等級面積百分比

5 結束語

筆者以西寧市城區地質災害為研究對象，遴選了海拔高程、地形相對高差、地層巖性、距公路距離、距斷裂構造距離、坡度、坡向、平面曲率、剖面曲率、地下水類型共10個評價因子，建立了地質災害危險性層次分析模型，獲取了10個評價因子的權重系數，構建了西寧市城區地質災害危險性評價數學模型。通過ArcGIS 10.6的空間疊加分析技術，依據已建的危險性評價數字模型，將獲取的10個單因素分區評價圖進行空間疊加處理，計算出了西寧市城區地質災害危險性綜合分區評價圖。從此圖得知，西寧市城區地質災害中低危險性區域面積最大，占全研究區面積的43%，其次是高危險性區，面積占全研究區面積的21%，然后是中危險性區域，占西寧市城區面積的19%，極高危險性區面積最小，占西寧市城區總面積的17%。本次研究成果對于西寧市城區的地質災害防治與工程建設具有重要參考價值。