基于極限平衡理論的臨坡地基承載力計算

鄒文龍 李星 張惠超

中鐵科學研究院有限公司，成都610032

在我國山區建設中，由于場地條件限制，大量基礎設施不可避免地修建在臨近山坡的地段，如跨河谷的橋梁樁基、高壓輸電線塔基礎等［1］。對于實際工程中的此類臨坡地基問題，GB 50007—2011《建筑地基基礎設計規范》中給出了相應的設計方法，但其規定多為經驗值，缺乏理論依據。為確保臨近邊坡建筑物的安全穩定，臨坡地基承載力的研究具有社會與工程意義。臨坡地基承載力問題是平地地基承載力問題的延伸，Meyerhof［2］最早研究了這個問題。此后，臨坡地基承載力引起了世界各國學者的關注，Kusakabe等［3］以及Georgiadis［4］為本問題的研究和發展做出了重要貢獻。我國學者很早也開始關注這個問題。早在1984年，張明楠等［5］基于彈性力學理論給出了斜坡頂部承載力的解。此后，以試驗［6-7］、理論計算［8］和數值仿真方法［9］為主要手段的成果大量涌現。尉學勇、趙煉恒、胡衛東等［10-12］雖給出了明確的計算方法，但都存在各自的問題，如基礎底面以下滑塊近似為等腰三角形，計算模型沒有真實地考慮基礎埋深等。另外，既有理論方法大多采用極限分析上限法開展臨坡地基承載力的研究，但設計人員更熟悉的卻是應用廣泛的極限平衡理論。本文在既有研究成果的基礎上，基于極限平衡理論，建立各滑塊的靜力平衡方程，通過引入非線性規劃算法解出臨坡地基極限承載力。

1 臨坡條形基礎地基破壞模式

臨坡地基的極限承載力與其達到極限狀態時所對應的臨界破壞模式密切相關，確定臨坡地基的破壞模式是進行臨坡地基承載力計算的重要前提。Meyerhorf［2］最早基于滑移線理論近似確定了臨坡地基破壞模式，由于此簡化模型能方便而不失精度地解決實際問題，此后關于臨坡地基承載力的研究普遍都采用這種破壞模式，本文也沿用該研究思路。

由于邊坡的存在，基礎下部地層中的應力分布與平地地基相比具有不對稱的特性，這將導致臨坡地基破壞模式的不對稱。另外，邊坡的存在也使臨坡側相較于遠坡側更容易發生破壞。綜上所述，為了給出合理的臨坡地基承載力解，結合實踐經驗并參考文獻［6，13］的既有研究成果，提出了由對數螺旋線和直線組成的破裂面的破壞模式。臨坡條形基礎地基破壞模式見圖1。假定坡度為β的邊坡坡頂地面水平，寬度為b的臨坡基礎埋深為d，基礎邊緣與坡頂邊緣的距離為λb，其中λ為臨坡距離與基礎寬度的比值。在均勻分布的極限壓力即條形基礎的極限承載力qu的作用下達到極限狀態，破裂面與坡面的夾角為η，基礎底面以下的滑塊為一個非等腰三角形ABC，其兩個底角為α1和α2；夾在主動區ABC和被動區ADKEM之間的過渡區ACD是一個頂角為θ的曲邊三角形區域，曲線邊界為對數螺旋線。

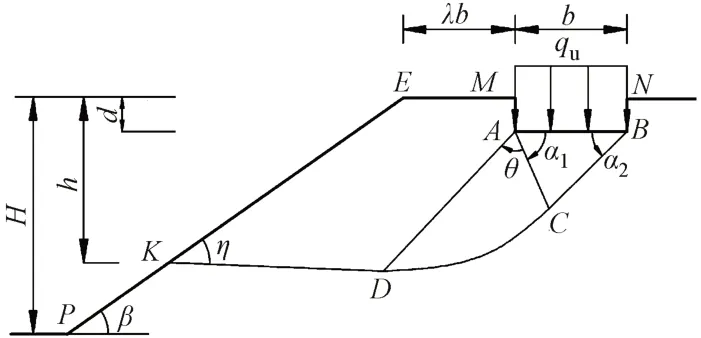
圖1 臨坡條形基礎地基破壞模式

根據上述臨坡條形基礎地基承載力計算的幾何分析模型，通過幾何關系可以獲得三角形ABC的兩條邊AC和BC的長度LAC、LBC，即

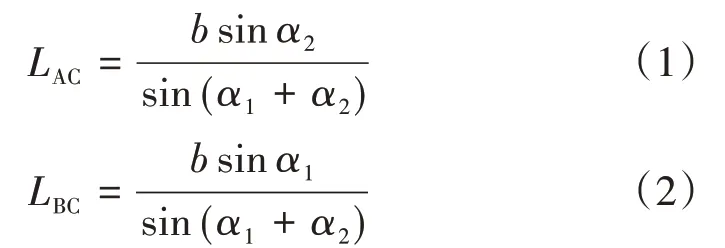
過渡區ACD的邊界為對數螺旋線，根據對數螺旋線的方程，邊長LAD計算式為

式中：φ為土體的內摩擦角。

為求解被動區滑面DK的長度LDK，可以通過點D與坡面的距離建立方程，化簡后為

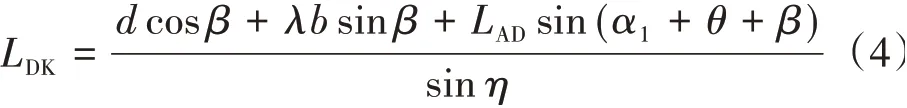
2 分析推導

2.1 被動區受力分析

對被動區ADKEM進行受力分析，其受力分析見圖2。其中，N1和T1為作用于界面DK上的法向力和切向力，N2和T2為作用于界面AD上的法向力和切向力，G1為被動區自身重力。

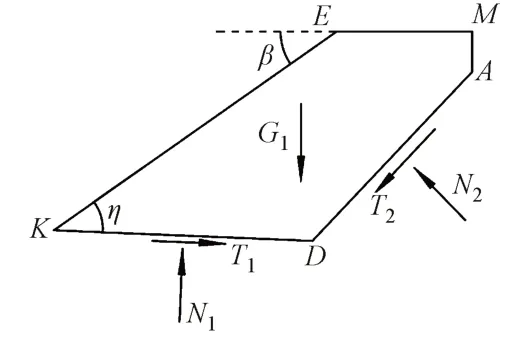
圖2 被動區受力分析

被動區在界面AD、DK上的合力及自身重力的作用下達到極限平衡狀態，水平和豎直方向的靜力平衡方程分別為

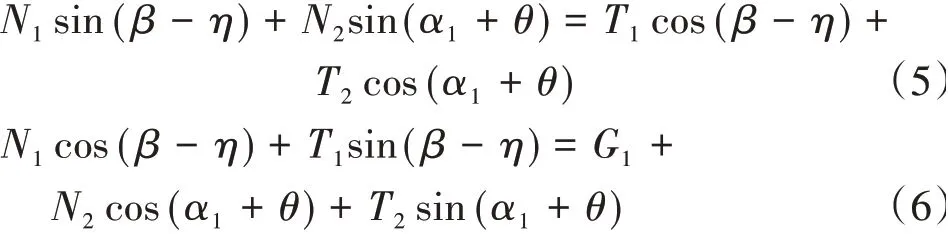
另外，被動區處于極限平衡狀態，界面DK和AD上的切向力和法向力滿足

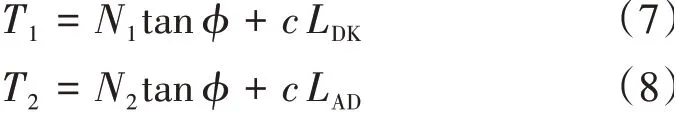
式中：c為土體的黏聚力。

被動區自身重力可表示為

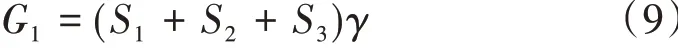
式中：γ為土體的重度；S1、S2、S3分別為△ADM、△DEM、△DEK的面積，S1=-d LADcos(α1+θ)/2，S2=λb[d+LADsin(α1+θ)]/2，S3=LDKhsinη/(2sinβ)，h為坡面剪出口距離坡面的深度，h=d+LADsin(α1+θ)+LDKsin(β-η)。

通過聯立式（5）—式（9）可以解出被動區邊界DK和界面AD上所受的力的表達式。這些力都是關于破壞模式的幾何參數α1、θ等的表達式。

2.2 過渡區受力分析

對過渡區ACD進行受力分析，見圖3。其中，N3和T3分別為作用于界面AC上的法向力和切向力，G2為過渡區自身重力。過渡區在界面AD、AC、CD上的合力及自身重力的作用下達到極限平衡狀態。

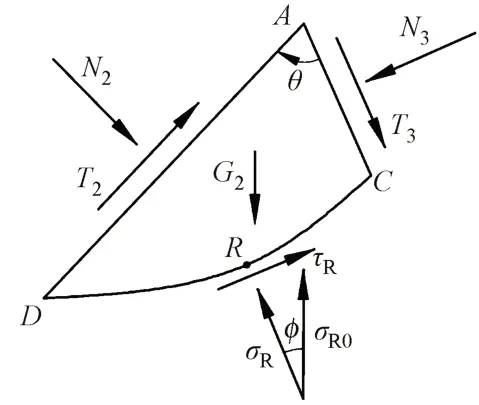
圖3 過渡區受力分析

假設界面CD上的任意一點R處所受的法向應力和切向應力分別為σR和τR，由于過渡區處于極限平衡狀態，即

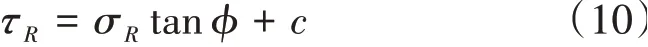
若σR與σRtanφ的合力為σR0，其與σR的夾角為φ。根據對數螺旋線的幾何性質，σR0是通過旋轉中心A的。因此，作用在點R上的合力就可以分解為指向旋轉中心的σR0和切向力c。另外，土壓力作用點一般位于界面的1/2到下1/3處之間，考慮到極限狀態時上部荷載遠大于破壞區域土體自重，為簡化分析，假設N2和N3都作用于各自界面的中點處。

對過渡區ACD以點A建立力矩平衡方程

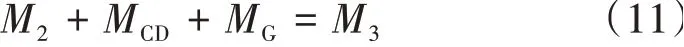
式中：M2、M3分別為N2、N3產生的力矩，M2=N2LAD/2，M3=N3LAC/2；MCD為CD界面上黏聚力產生的力矩，為過渡區重力力矩，MG=γSACDL，SACD為過渡區ACD的面積，為過渡區重力力矩的力臂。

根據對數螺旋線幾何性質可知

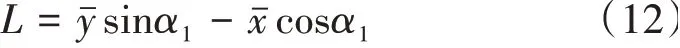
式中：、為形心坐標。

、的表達式分別為

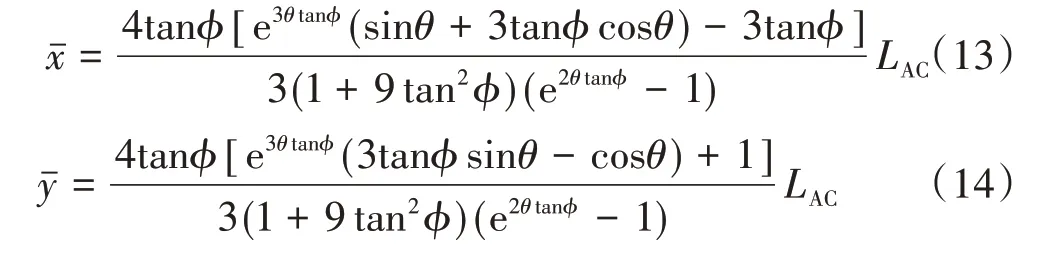
整理式（11）—式（14），N3可以寫為關于N2的表達式。由于過渡區處于極限平衡狀態，T3可以寫為

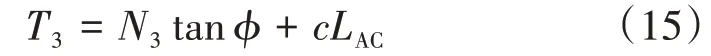
N2和T3是一個僅關于破壞模式的幾何參數的表達式。

2.3 主動區受力分析

對主動區ABC進行受力分析，見圖4。其中，N4和T4分別為作用于界面BC上的法向力和切向力，G3為主動區ABC的重力。

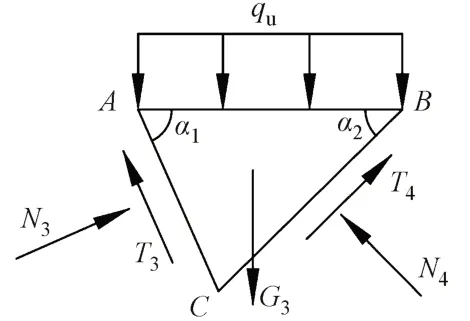
圖4 主動區受力分析

主動區在界面AC、BC、AB上的合力及自身重力的作用下達到極限平衡狀態，水平方向和豎直方向的靜力平衡方程分別為

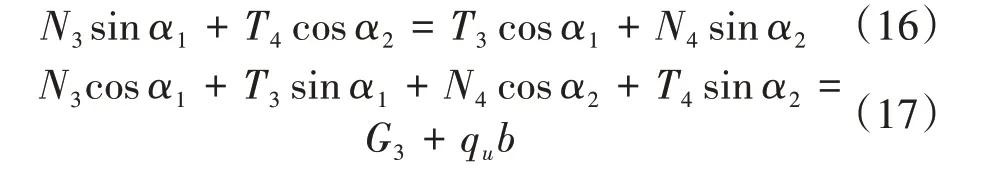
G3表達式為

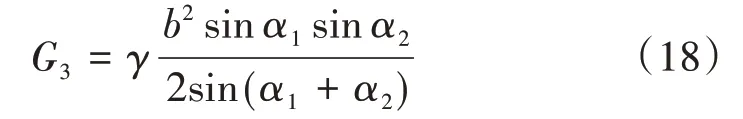
由于主動區處于極限平衡狀態，T4可以寫為

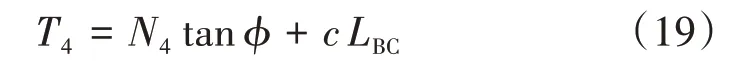
通過聯立式（16）—式（19）可以解出主動區界面BC上的法向力N4和切向力T4以及作用在AB界面上的極限荷載qu。這些力都是關于破壞模式的幾何參數的表達式。

2.4 臨坡地基承載力的極限平衡解

由于臨坡地基極限承載力qu表達式僅與破壞模式的幾何參數α1、α2、θ和η有關，則地基極限承載力實際上可以看做為這些幾何參數的函數，即

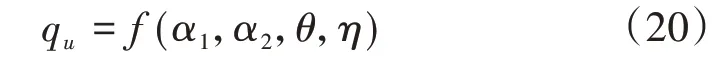
式（20）是通過聯立式（1）—式（19）解得的。其中，考慮到各角度和長度應具有物理意義，且點C、點D處破裂面應光滑連續，各幾何參數的取值應滿足

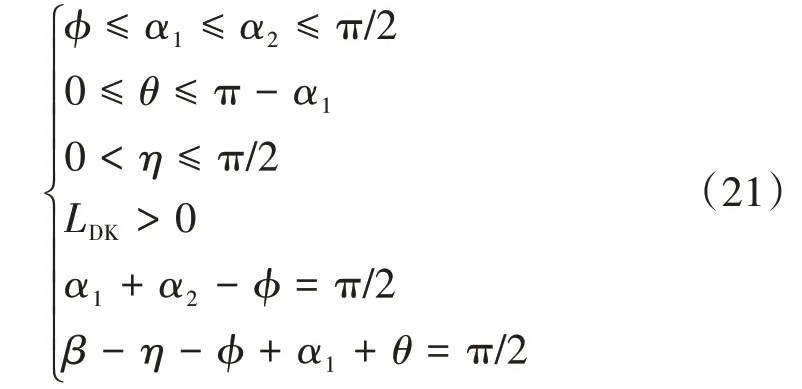
根據潘家錚［14］最大最小原理，式（20）的最小值就是地基極限承載力。于是該問題轉化為：破壞模式的幾何參數在其各自合理的范圍內變化時，通過式（20）求得極限承載力的最小值。這是一個非線性規劃問題，可以通過MATLAB工具箱中的fmincon求解。

3 算例驗證與分析

前文以極限平衡理論為基礎，建立了臨坡地基極限承載力的計算方法，為驗證其合理性與可行性，有必要與既有研究成果對比。

3.1 算例一

蔣洋等［15］利用有限元數值模擬研究了臨坡地基極限承載力，文中算例基礎寬度b=1 m，地基土重度γ=17 kN/m3，邊坡的坡度為30°。以文獻［15］中的算例為例，采用文獻［16］方法及本文方法計算不同地基土的抗剪強度參數c、φ以及基礎埋深d時臨坡地基承載力，見表1。可知：本文方法與兩種既有方法的計算結果吻合，將兩種既有方法的平均值作為參照，本文方法與平均值的最大相對誤差在10%以內，這表明了本文方法的合理性與可行性。由算例的幾何條件可以發現，本文方法不僅適用于臨坡基礎與坡頂邊緣的距離不為0的情況，也適用于基礎有一定埋深的情況。

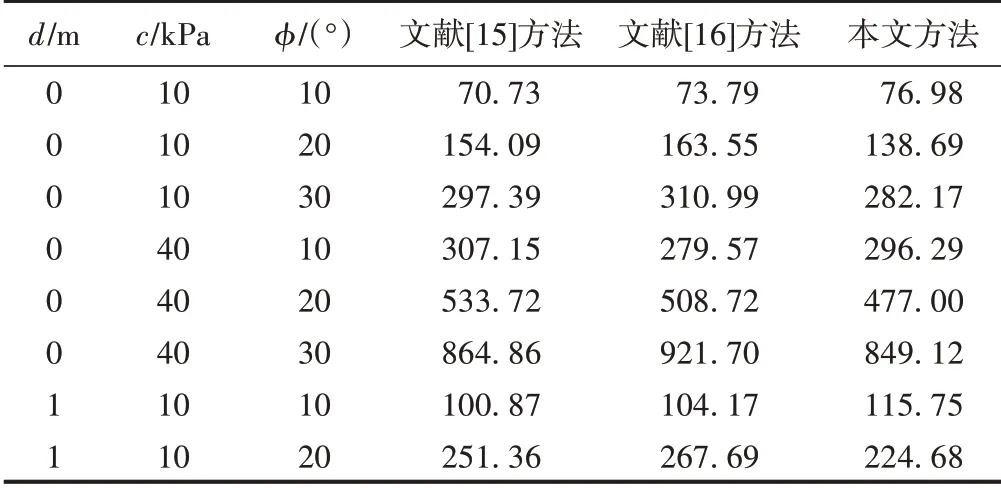
表1 算例一臨坡地基承載力對比 kPa

3.2 算例二

趙明華等［17］將極限分析上限法與有限元法相結合，對臨坡地基承載力開展研究，并給出了大量算例。以文獻［17］中的算例為例，采用文獻［17］方法及本文方法計算的臨坡地基承載力見表2。其中基礎寬度選取為1 m，地基土的重度為20 kN/m3。

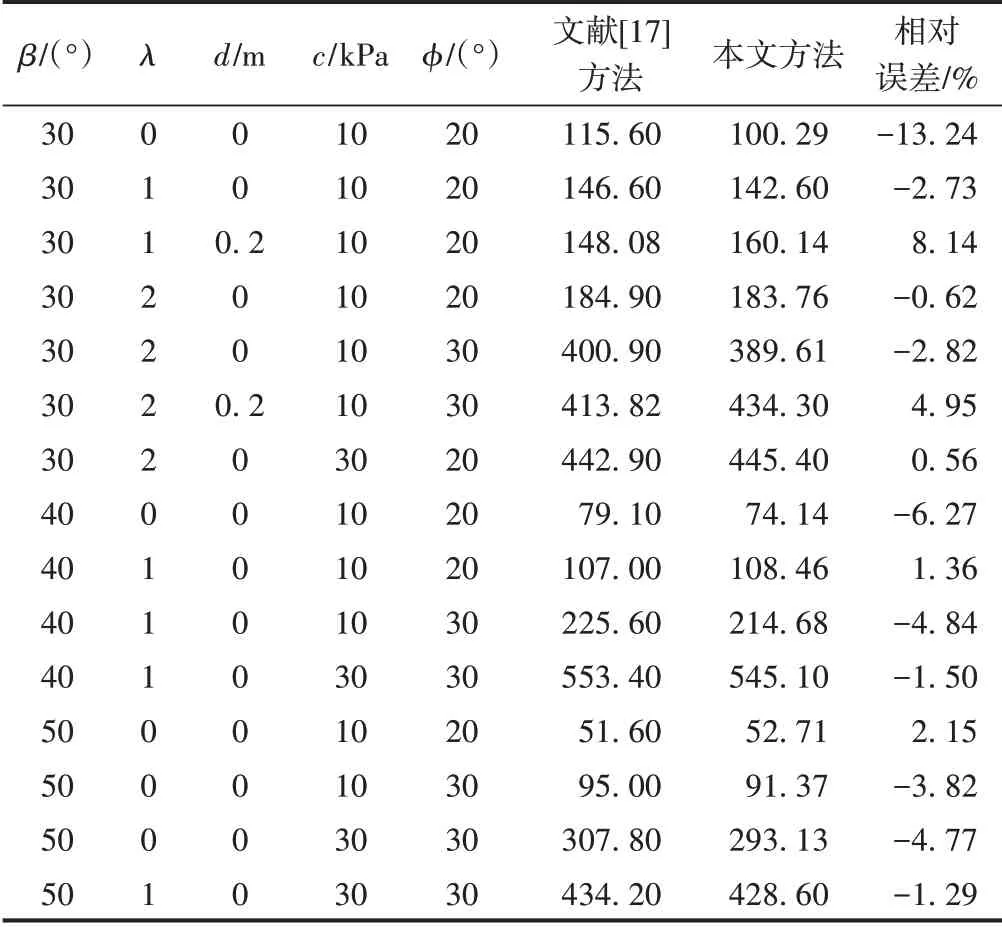
表2 算例二臨坡地基承載力對比 kPa

由表2可知：①本文提出的基于極限平衡理論的臨坡地基承載力計算方法的計算結果與上限有限元方法結果的最大相對誤差在14%以內，且絕大部分都在5%以內，這表明了本文方法的合理性與正確性。②本算例中不同工況間的變量包括了坡角、臨坡距離、基礎埋深、黏聚力及內摩擦角，且不同工況下均能獲得與既有方法十分吻合的計算結果，也表明本文方法具有廣泛的適用性。③通過控制變量法比較各工況下的計算結果，不難發現，臨坡地基承載力隨坡度的增大而減小，隨地基土的抗剪強度指標的增大而增大，隨臨坡距離的增大而增大，隨基礎埋深的增加而增大。上述規律都符合工程實踐，也側面反映出本文方法的合理性。

3.3 算例三

臨坡地基破壞模式的合理確定關乎所求極限承載力的正確性。為驗證本文方法所求結果對應的破壞模式的合理性，以文獻［18］中的算例為例，采用文獻［18］方法及本文方法對比不同工況下臨坡地基的破壞模式，結果見圖5。其中，工況一的邊坡坡角為30°，基礎寬度為1 m，地基土重度為20 kN/m3，內摩擦角為40°，c/（γb）=1；工況二的邊坡坡角為20°，基礎寬度為1 m，地基土重度為20 kN/m3，內摩擦角為10°，c/（γb）=0.5。

由圖5可知，本文方法所得的破壞模式與利用數值模擬方法所得結果吻合良好。這表明本文方法不僅能獲得合理可靠的臨坡地基承載力值，也可以獲得合理可靠的臨坡地基破壞模式，為防治相關地質災害和巖土工程設計提供依據。

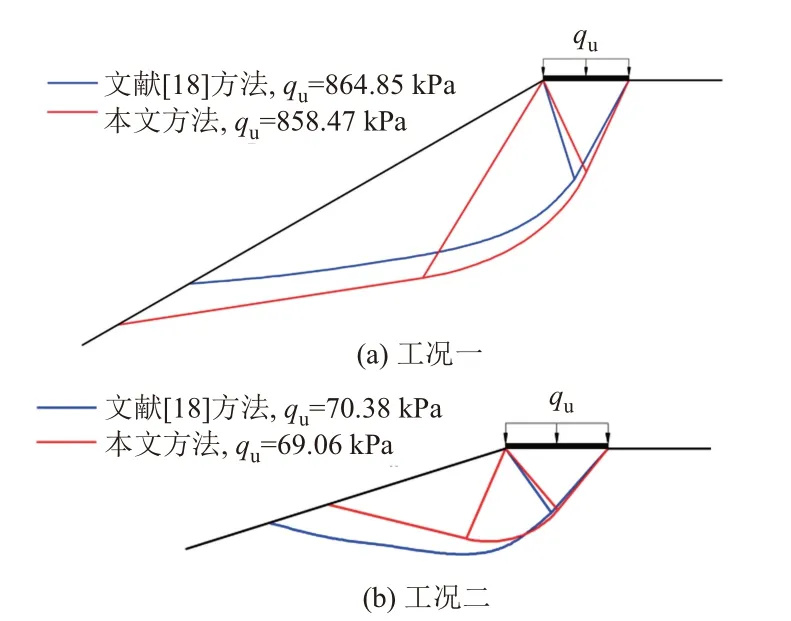
圖5 算例三不同工況時邊坡破壞模式對比

3.4 算例四

臨坡建筑物地基受邊坡影響的臨界距離是實際工程中遇到的重要問題。GB 50007—2011中雖有相關規定，但其中規定缺乏理論依據。為此，應探討臨坡建筑物安全距離及其規律。

以基礎寬度為1 m，重度為20 kN/m3，c/（γb）=1的邊坡為例，采用本文所提出方法，討論不同坡角和內摩擦角情況下臨坡地基承載力與臨坡距離比的關系，結果見圖6。可知：①當地基土的抗剪強度一定時，無論坡角大小如何，隨著臨坡距離的增大，臨坡地基的極限承載力都將逐漸增大并趨近于同一個值，即平地地基承載力。但達到平地地基承載力時所對應的臨坡距離比與坡角相關，坡角越大，邊坡對地基承載力的削弱作用越大，使邊坡不再產生影響的臨界距離也越大。②不同工況下所對應的臨界距離是顯著不同的。以β=45°，φ=30°的工況為例，當臨坡距離比為5時，邊坡對地基承載力的削弱作用仍存在，而按照現行規范進行處理是偏于危險的。

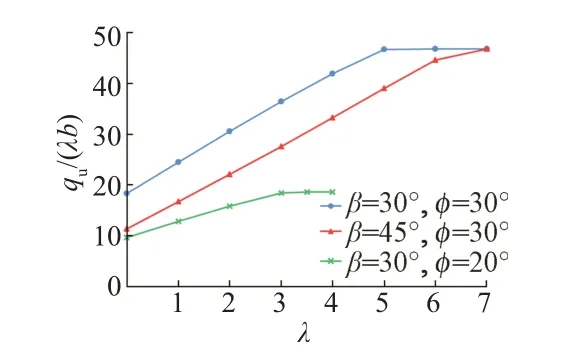
圖6 算例四臨坡地基承載力與臨坡距離比關系

4 結語

通過臨坡地基破壞模式中各滑塊的靜力平衡方程，給出了臨坡地基極限承載力的計算步驟，引入非線性規劃算法，建立了臨坡地基承載力的計算方法。

采用多個既有算例的數據，利用本文方法進行計算，并與既有結果進行對比。本文方法與各數值模擬結果均吻合較好，證明本文方法兼具合理性及廣泛的適用性。所求破壞模式結果與既有方法結果一致也展現出本文方法的可靠性。

通過臨坡臨界距離的討論，發現邊坡對地基承載力削弱效果消失的臨界距離與多方面因素有關，而現行規范的規定可能使設計偏于危險。本文方法可以為防治相關地質災害和巖土工程設計提供依據。