基于改進TOPSIS決策方法的鐵路線路方案優選研究

顏文

中鐵第一勘察設計院集團有限公司，西安710043

截至2020年底，全國鐵路運營總里程已經達到14.6萬km，其中高速鐵路運營里程3.9萬km以上，全國路網密度達152.1 km/萬km2。隨著鐵路行業的快速發展，鐵路線路走向方案決策的重要性凸顯出來，較優的線路走向方案將會提高整個路網的運營效率。現有的鐵路線路方案優劣性評價僅僅停留在代數概念，不符合人類思維的邏輯判斷，無法直觀地理解方案的優劣性。依據國外文獻對決策問題的分類，傳統

TOPSIS（Technique for Order Preference by Similarity to an Ideal Solution）方法屬于一種多方案、多目標的決策方法，即對一組離散型的決策變量、具有有限數量的備選方案進行決策評價，并根據排序結果優選出最佳方案［1-5］。

TOPSIS方法能夠充分利用復雜、離散的原始數據實現對多指標線路走向決策方案的綜合評價。對于一個有待決策的問題，其最優方案應綜合考慮備選方案距最優方案和最劣方案的距離，即距離正理想解最近、距離負理想解最遠的方案。因此，該方法也稱為理想解法。通過計算相對貼近度來衡量備選方案的排序情況［6］，也可以顯示待決策方案間的優劣差距。通過模型轉換，使復雜的鐵路線路走向方案決策問題便于理解和應用。

改進TOPSIS方法利用有限的數據信息構造出空間特征向量，通過計算向量夾角余弦來度量向量之間的關聯程度，通過數形結合的方式將代數概念轉化為幾何概念，在解決多方案、多目標決策問題中具備一定的適用性。陳為公等［6］將改進TOPSIS方法應用于建筑供應商的比選研究中；張卉［7］將改進TOPSIS方法應用于農產品營銷渠道選擇研究中。

本文以改進TOPSIS決策方法作為鐵路線路方案比選的理論支撐，引入向量夾角余弦、貼近度等概念，得到線路方案的排序結果，以提高方案決策的科學性和準確性，從而科學合理地對鐵路線路走向方案進行決策。

1 改進TOPSIS方法理論

以待評價方案向量d1與最優方案（正理想解）向量d+為例，其三維空間的向量夾角θ的余弦距離sim（d1，d+）如圖1所示。

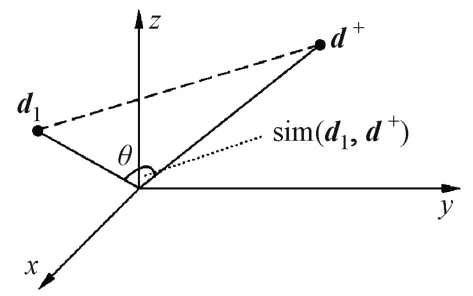
圖1 三維空間的向量夾角余弦距離

將改進TOPSIS方法應用到鐵路線路方案比選研究中，根據選取的評價指標體系、指標權重確定方法以及TOPSIS方法原理，建立基于改進TOPSIS方法的鐵路線路方案比選流程，如圖2所示。

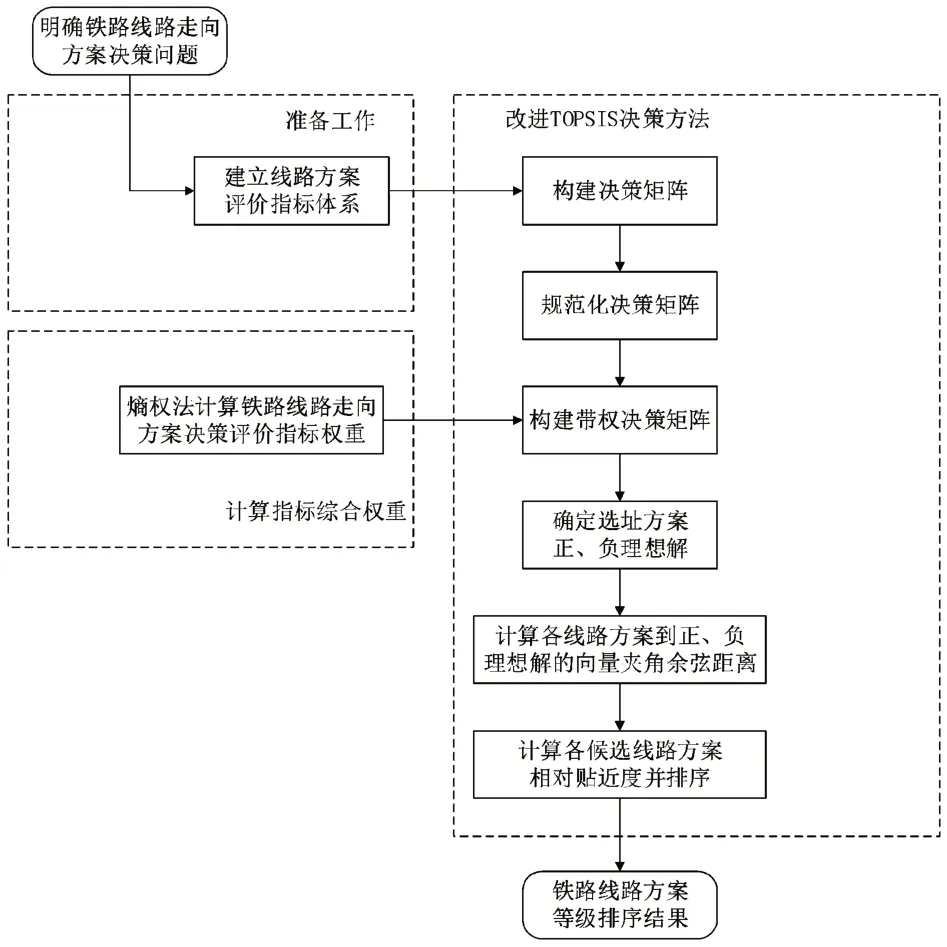
圖2 基于改進TOPSIS方法的鐵路線路方案比選流程

首先，構建多指標決策矩陣X。設鐵路線路方案有n個待評價方案，對于每一個評價方案有m個評價指標，則決策矩陣為

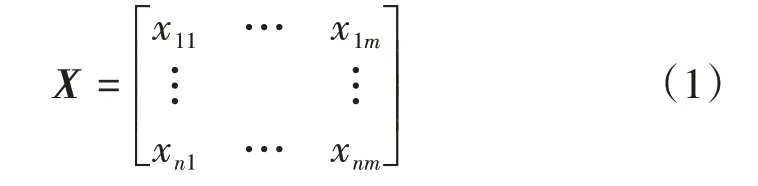
式中：xij是第i個待評價方案下第j個評價指標的值，i=1，2，…，n，j=1，2，…，m。

令表示第j個評價指標下的指標值之和，則決策矩陣X歸一化后的矩陣P為

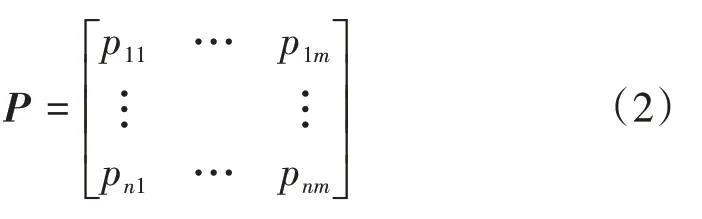
計算加權決策矩陣D，表達式為

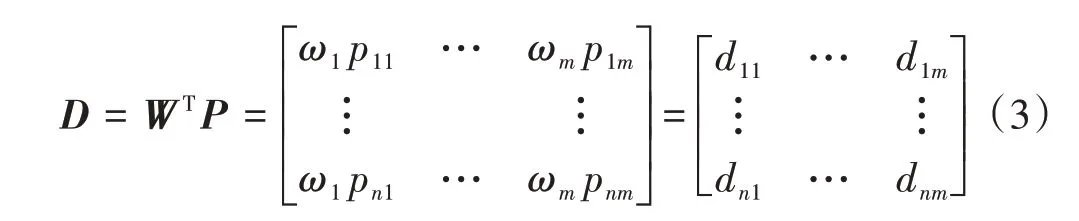
式中：W是權重矩陣；ωj是第j個評價指標的權重值，且

然后，確定正理想解向量d+和負理想解（最劣方案）向量d-。對于效益型指標，指標值越大，方案越優；對于成本型指標，指標值越小，方案越優。因此，正、負理想解向量定義分別為

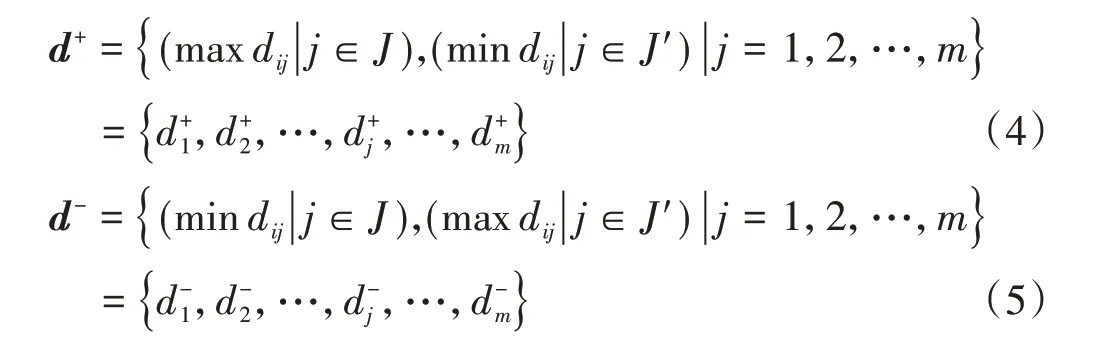
式中：J是與效益型有關的評價指標集合；J′是與成本型有關的評價指標集合。

計算各線路方案到正、負理想解在三維空間的向

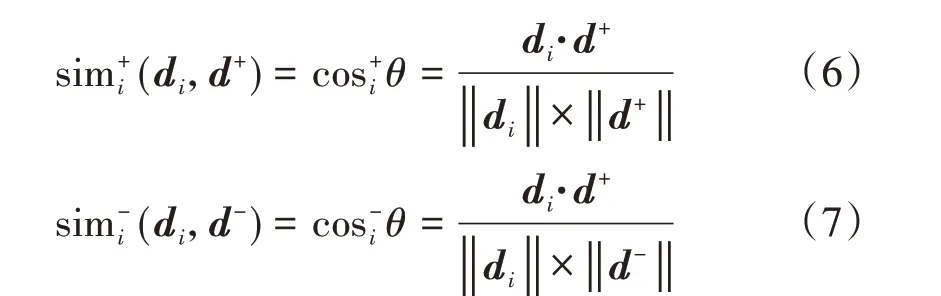
式中：d i是第i個待評價方案向量。

各線路方案到理想方案的貼近度Gi是衡量各線路方案到最優方案的距離與正、負理想解之間距離的比值，其取值范圍為[0，1]，表達式為

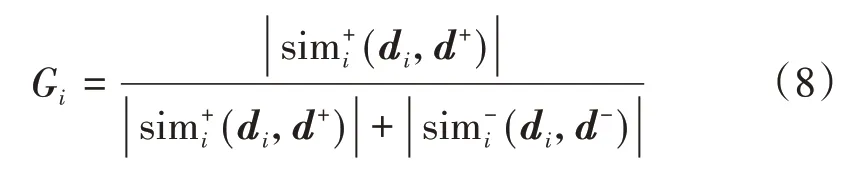
最后，根據貼近度的大小進行降序排序，得到鐵路線路方案的優劣次序。Gi值越接近于1，表示該方案越接近最優方案；反之，貼近度Gi值越接近于0，表示該方案越接近最劣方案。

2 工程概況

西寧至青海湖至茶卡（察汗諾）鐵路［8］位于青海省東中部地區。項目起自西寧市，向東利用既有鐵路輻射海東市平安區，向西新建線路經多巴新城、湟源縣折向西南，經海南州共和縣至青海湖二郎劍景區，后經黑馬河至海西州烏蘭縣茶卡鎮，并利用既有茶卡支線鐵路電氣化改造至青藏鐵路察汗諾站。西寧至青海湖至茶卡（察汗諾）鐵路運營長度348.8 km，其中新建線路長度275.2 km，新建橋梁90.28 km，新建隧道91.66 km，橋隧比為66.11%。新設多巴新城、湟源南、日月山、倒淌河、共和、青海湖南、黑馬河、茶卡南等15處車站。

該鐵路是蘭西城市群城際鐵路的骨干線路，將直接連通青海湖、茶卡湖與城市群核心城市西寧，不僅是構筑青海省西部黃金旅游通道（蘭州—西寧—泛共和盆地—青海湖—茶卡—柴達木盆地）的重要交通基礎設施，還是青海省唯一不通鐵路的海南藏族自治州州府駐地共和縣對外出行的第一條鐵路。該線路對于解決青海省交通基礎設施發展不平衡、不充分問題具有重大意義。

考慮線路與城市規劃的關系、多巴新城站位、征地拆遷等因素，結合西寧市地方政府意見，對西寧西至湟源段線路預設了兩個方案，即湟水河南岸沿青藏鐵路布線（簡稱AK方案）和湟水河北岸沿京藏高速公路布線（簡稱A10K方案），如圖3所示。

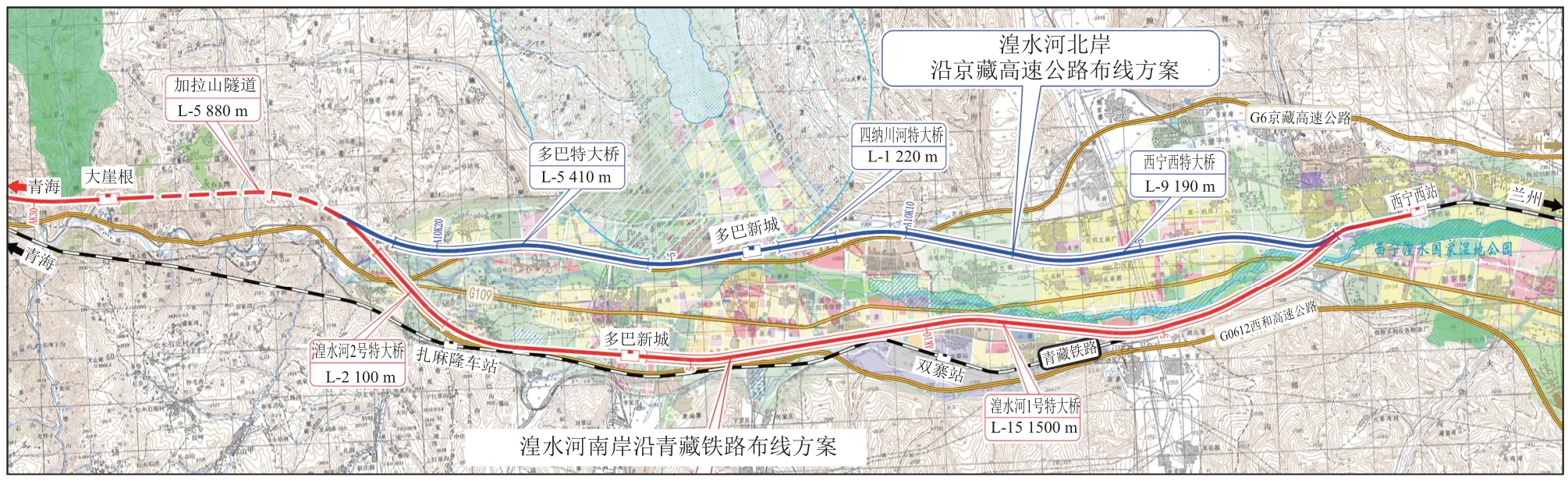
圖3 西寧西至湟源段線路方案示意

2.1 方案概述

2.1.1 湟水河南岸沿青藏鐵路布線方案

線路出西寧西站，跨至湟水河南岸，利用既有青藏鐵路、西和高速公路形成的既有通道布線，有條件時盡量并行既有鐵路；經雙寨，于教場河西側利用規劃預留的鐵路客運站用地設多巴新城站；繼續西行，于扎麻隆村南側跨越京藏高速公路、湟水河，于扎麻隆村進入隧道，穿越華石山，經東峽鄉至湟源。

根據該方案，區段線路長27.00 km，橋隧總長22.03 km，橋隧比81.59%，靜態投資24.48億元。

2.1.2 湟水河北岸沿京藏高速公路布線方案

線路自西寧西站引出，走行于湟水河北岸，沿規劃城市主干道穿越海湖新區規劃區，跨越京藏高速公路，并行高速公路布線，于多巴鎮和京藏高速公路之間設多巴新城站；繼續向西，于扎麻隆村進入隧道并與AK方案銜接。

根據該方案，區段線路長25.70 km，橋隧總長20.60 km，橋隧比80.15%，靜態投資23.83億元。

2.2 方案比選

1）對多巴新城的帶動作用

AK方案：多巴新城站位于湟水河南岸，緊靠湟水河谷規劃片區；但有京藏高速公路、湟水河和G109等線形障礙的阻隔，旅客進出站有所不便。

A10K方案：多巴新城站位于湟水河谷規劃片區及西納川規劃片區之間，乘客進出站距離短，出行便利，對于多巴新城建設開發帶動作用更優。

2）對湟水河水文條件的影響

AK方案：兩次跨越湟水河主河槽，在雙寨附近為繞避現狀拆遷工程，順河道布線長達7 km，對湟水河水文條件有一定影響。

A10K方案：不跨越湟水河主河槽，順河布線段落較短，通過防護評價難度小。

3）與環境敏感點的關系

AK方案：不可避免地穿越湟水河濕地公園保育區、恢復重建區，穿越長度0.3 km。

A10K方案：穿越西寧五水廠飲用水源地二級保護區陸域范圍，穿越長度約2.3 km。

4）征地拆遷工程量

AK方案：長大段落利用既有青藏鐵路通道布線，征地拆遷工程量較少。

A10K方案：利用既有京藏高速公路通道布線段落短，且通過現狀多巴鎮區邊緣，拆遷工程較大，較AK方案增加拆遷房屋面積約1.3萬m2。

5）線路直順性、線路長度、工程投資

AK方案：線形較迂回，線路較長，投資較大。

A10K方案：線路短直，相比AK方案，線路長度縮短1.30 km，投資節省約0.65億元。

6）與地方政府意見的符合性

AK方案：符合多巴新城的城市總體規劃，也符合西寧市地方政府的意見。

A10K方案：在本項目預可研審查過程中，西寧市地方政府明確表示反對湟水河北岸設站的A10K方案。因為A10K方案切割城市規劃段落過長，未利用規劃預留的鐵路客運站用地，與多巴新城的總體規劃有所不符。

兩種方案比選見表1。

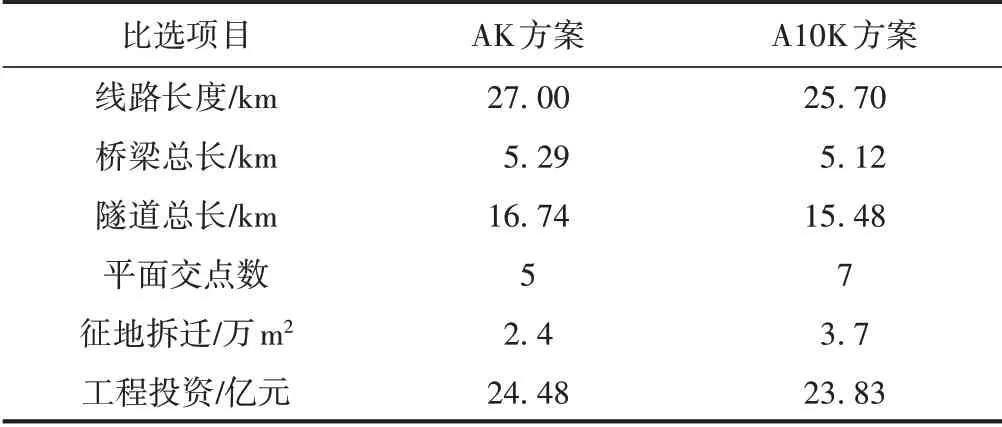
表1 西寧西至湟源段線路方案比選

綜上，A10K方案雖線路短直、旅客乘車較便利，但該方案切割城市規劃較嚴重，與多巴新城總體規劃不符，且征地拆遷工程量較大。而AK方案較好地利用了既有青藏鐵路通道布線，切割城市規劃段落短；利用規劃預留的鐵路客運站用地設置多巴新城車站，與城市規劃相容性好；對環境敏感區影響小，也符合西寧市地方政府的意見。

因此，推薦采用湟水河南岸沿青藏鐵路布線方案（AK方案）。

3 線路方案TOPSIS決策評價分析

1）確定權重

根據方案概述，對各指標的數值進行歸一化處理，消除量綱影響之后，采用熵值法［9］對各指標進行賦權，結果見表2。

表2 評價指標權重

2）計算標準化矩陣

根據式（1）和式（2），計算歸一化矩陣P。算得P=

3）計算加權決策矩陣

根據式（3），計算加權決策矩陣D。算得D=

4）確定正、負理想解

根據式（4）和式（5），計算正、負理想解d+、d-。算得d+=［0.019 4 0.183 1 0.112 2 0.035 6 0.080 0 0.005 6］，d-=［0.020 4 0.256 4 0.173 1 0.034 5 0.074 0 0.005 7］。

5）計算向量夾角余弦距離

根據式（6）和式（7），利用Matlab軟件計算得到AK和A10K方案到正、負理想解的向量夾角余弦距離，進而得到其貼近度排序。結果見表3。可知，湟水河南岸沿青藏鐵路布線方案（AK方案）更優。改進TOPSIS模型的評價結果與實際論證結果一致，這說明本研究建立的方案決策模型具有一定的可行性和有效性。

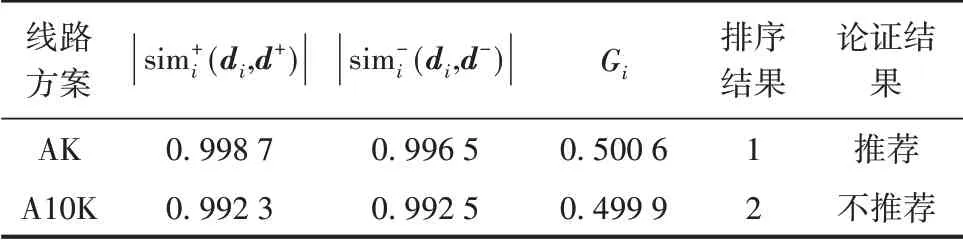
表3 各方案與正、負理想解的距離及貼近度排序

4 結語

針對鐵路線路走向方案選擇問題，本文以西寧至青海湖至茶卡鐵路的西寧西至湟源段線路布線方案比選為工程實例，選取了合適的工程數量因子作為評價指標，既可避免因素過多互相干擾，又能避免指標內容過于繁瑣難以操作，使評價方法得到簡化又不失有效性。

改進TOPSIS決策方法能夠將復雜的代數概念通過數形結合的方式轉化為幾何概念，更符合人類思維的邏輯判斷，并能夠實現多目標的決策優化，可以作為鐵路線路方案比選的一種推薦方法。