Sobolev方程的等參有限元法

劉智新，張媛，宋士倉

(1.鄭州大學數學與統計學院，河南鄭州450001;2.鄭州鐵路職業技術學院數學教研室，河南鄭州451460)

1.引言

考慮如下的Sobolev方程

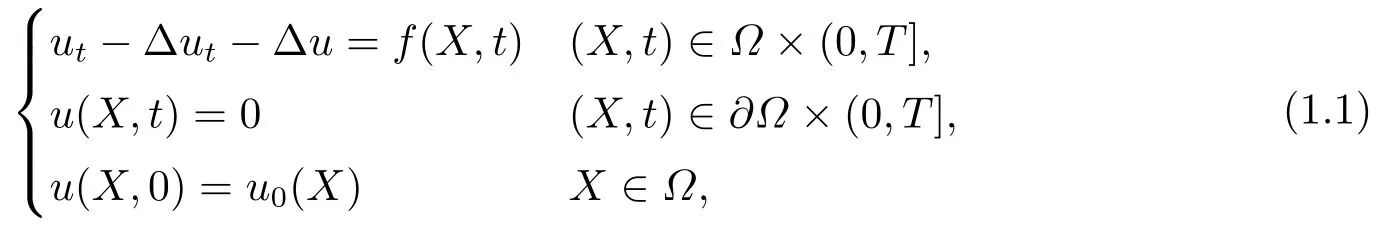
其中Ω?R2為具有光滑邊界?Ω的有界區域，X=(x，y)，u0(X)，f(X，t)是已知函數.

Sobolev方程在流體穿過裂縫巖石的滲透理論，土壤中的濕氣遷移問題，不同介質中的熱傳導問題，黏土的加固理論等許多數學物理問題中有著廣泛的應用.關于其數值方法的研究已經有很多，如文[1]討論了標準混合有限元方法，文[2-3]介紹了H1-Galerkin混合有限元方法，文[4-5]分別討論了非協調元方法和弱Galerkin有限元方法.進一步的，文[6-8]討論了非線性的情形，并給出了相應數值方法的收斂性分析.關于這些數值方法的文獻還有很多，但這些文獻主要是在凸多邊形區域上討論的.對于多角形區域，由于解的光滑性不夠，不宜采用高次元去逼近，否則達不到提高精度的目的.在實際生活中會經常遇到曲邊區域的情況，當用有限元方法去處理時，通常的方法是用多角形區域(直邊有限元)去逼近，但由于邊界處的誤差較大，也會影響精度.若通過對邊界處的網格加密來減少誤差，這樣也會導致計算量的巨大增加.因此為了使收斂階不受損失，我們可以采用等參有限元去逼近曲邊區域.

目前討論等參有限元逼近的文獻也比較多，在此我們簡要描述與之相關的一些主要貢獻.設u是某個方程的變分問題的解，Ω是具有光滑邊界的有界區域，uh和Ωh分別是u和Ω的近似值.文[9-10]中詳細介紹了等參有限元方法，并應用二次Lagrange等參元去逼近具有齊次Dirichlet邊界的二階橢圓問題，最終得到了‖-uh‖H1(Ωh)=O(h2)的誤差估計，其中～u是u到Ωh的某種延拓.同時由于其考慮了數值積分，因此只要積分點位于Ω∩Ωh上，便能夠定義近似問題而無需將函數延拓到Ωh上，文[11]給出了不使用數值積分的誤差估計.基于這種思想，許多學者將等參有限元方法應用到其他問題中，如[12-14]討論了用等參混合有限元方法去求解四階橢圓邊值問題和Stokes問題，得到了與凸多邊形區域上同樣的收斂階.文[15-16]將等參有限元方法應用到了橢圓界面問題中，得到了比傳統的有限元方法更好的收斂階.進一步的，文[17]在文[10]中介紹的等參有限元方法基礎上，提出了另一種估計思路.它討論了如何去構造一個映射Φh:Ωh→Ω，該映射對于任意維數空間都是有效的，可以很自然的將Ω區域上的函數延拓到Ωh上，并給出了相關的誤差估計.然后應用k次Lagrange等參元討論了曲邊區域上的二階橢圓問題，得到了‖u-uh°‖H1(Ω)=O(hk)的誤差估計.但是以上討論都是基于定常問題，就作者所知，將等參有限元方法應用于非定常問題的文獻還比較少，文[18]基于文[10]中提出的思想討論了拋物方程的等參有限元方法，其中引入了Ritz投影，并給出了嚴格的證明，最后討論了全離散格式下真解和有限元解在Ω∩Ωh上的L2模誤差估計.文[19]將文[17]中的思想進一步應用到了拋物方程中，并分別討論了真解和有限元解在半離散和Crank-Nicolson全離散格式下的誤差估計.但上述文獻只是給出了理論估計，并沒有給出相應的數值算例.

本文主要研究當求解區域Ω?R2為具有光滑邊界?Ω的有界區域時，應用文[17]的思想去求解問題(1.1).給出了半離散問題和向后歐拉全離散格式下解的存在唯一性的證明，并且分別討論了真解和有限元解之間的誤差估計.最后給出了一個數值算例，進一步驗證了理論分析的結果，其結果表明，采用等參有限元去逼近曲邊區域可以達到和凸多邊形區域上同樣的收斂階.

在本文中我們用C表示一個與h無關的大于0的常數，不同的地方大小可能不同.

2.預備知識

為了下面證明的需要和方便，首先給出一些定義和引理.

我們用Wm，p(Ω)表示通常的Sobolev空間，其中m≥0，1≤p≤∞，其范數定義如下

當p=2時，記Wm，p(Ω)=Hm(Ω).并且相關的范數記作如下:

設Y是Banach空間，其范數記為‖·‖Y，對映射φ:[0，T]→Y，定義

為了引進全離散逼近格式，將區間[0，T]劃分為:0=t0＜t1＜···＜tN=T，Δt=為時間步長，其中N為正整數.同樣定義

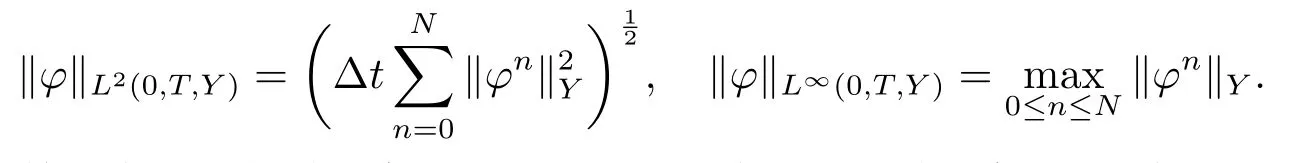
另外關于等參有限元的詳細介紹可見文[9-10]，此處不再詳細介紹.現在我們用k次Lagrange等參有限元對區域Ω進行剖分，Jh為一族正則的等參有限元剖分，Ω的近似區域為Ωh=其中T為剖分單元，記h為剖分單元的最大直徑.我們記ΠT為單元T上的插值算子，其具體定義可見文[9-10]，又由文[17]知，存在可逆映射Φh:Ωh→Ω，其逆為則有Φh|T:T→，且同理，有Φh:→X.定義Πh為整個Ωh區域上的插值算子，對則有

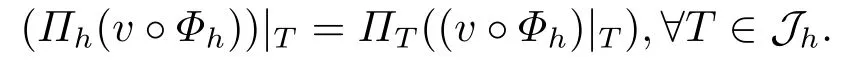
由此引入(Ωh)的有限維子空間

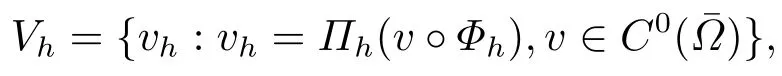
及)的有限維子空間

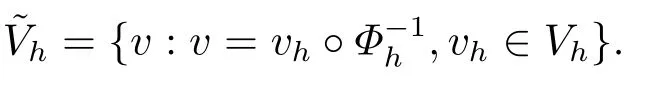
由文[17]，我們可以得到如下三個引理.

引理2.1設Jh為一族正則的等參有限元剖分，用J(Φh)表示映射Φh的Jacobi行列式，則存在一個與h無關的常數C，使得

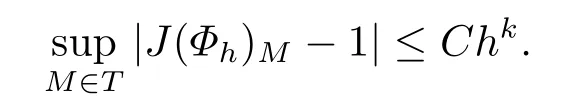
引理2.2假設v∈C0(∩Hk+1(Ω)，令則存在一個與h無關的常數C，然后有

引理2.3設0≤m≤k+1，則范數‖vh‖Hm(Ωh)和是等價的.

3.半離散問題的誤差估計

問題(1.1)的變分問題為，求u:[0，T](Ω)，使得

則問題(3.1)對應的半離散逼近格式為：求uh:[0，T]→Vh，滿足

定理3.1問題(3.2)有唯一解.

證設是空間Vh的一組基，則uh可以表示為

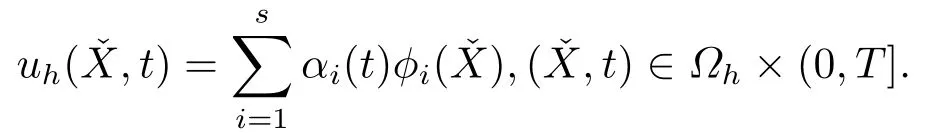
其中

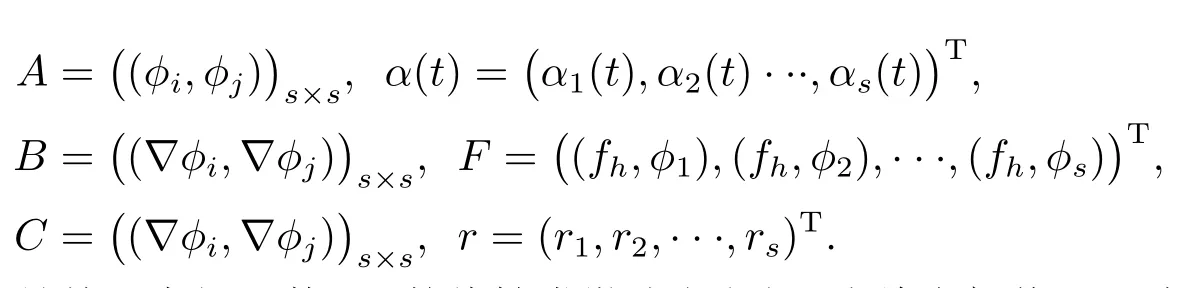
顯然(3.3)式是關于未知函數α(t)的線性常微分方程組，當給定初值α(0)時，由常微分方程理論知(3.3)式存在唯一解α(t)，從而半離散問題(3.2)存在唯一解uh(X，t).

定理3.2設u和uh是問題(3.1)和問題(3.2)的解，f∈L2(0，T，L2(Ω))，u∈L2(0，T，Hk+1(Ω))，ut∈L2(0，T，Hk+1(Ω))，并且ut，?ut，?u有界，則有如下估計

證首先我們引入一個穩態問題，即尋求輔助函數χh∈Vh，使得

令u°Φh-uh=u°Φh-χh+χh-uh=θ+η，其中θ=u°Φh-χh，η=χh-uh.將(3.1)式改寫為

(3.5)式減去(3.2)式得

其中G1=(?χh，t，?vh)-(?ut，?(vh°))，G2=(?χh，?vh)-(?u，?(vh°))，G3=.

在(3.5)式中令vh=η，則左端為

同理

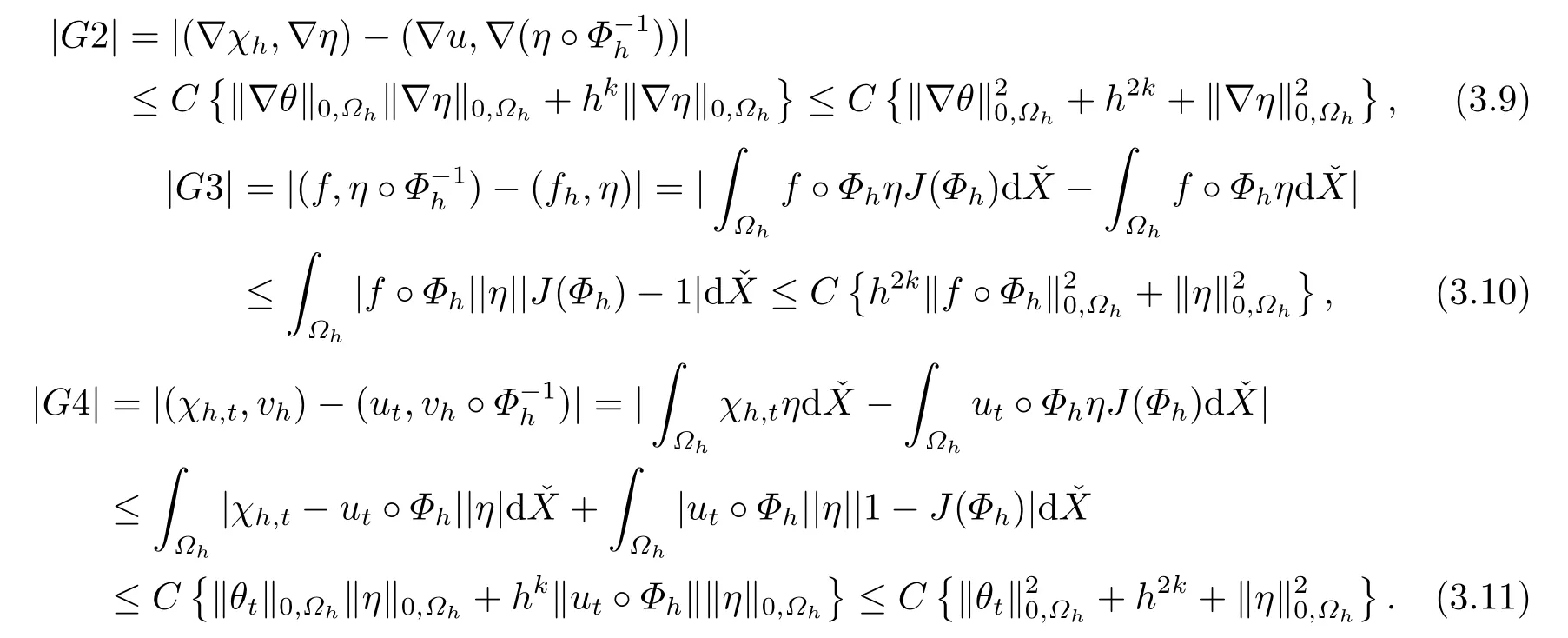
將(3.8)-(3.11)式代入(3.5)式，則有

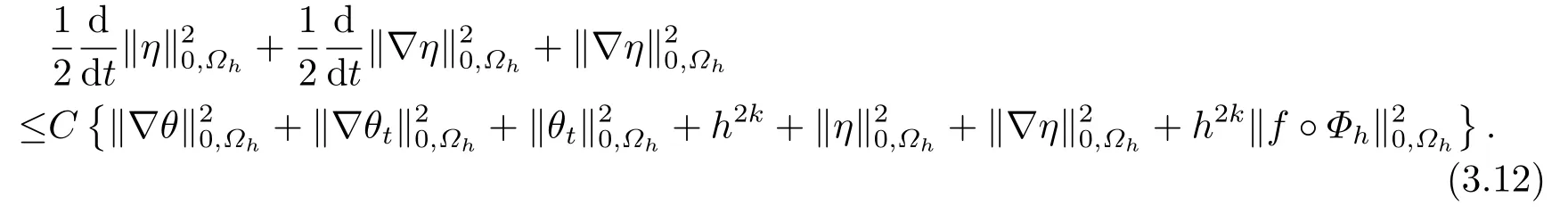
將(3.12)式從0到t積分，可得

利用Gronwall引理，存在常數C，使如下估計式成立

對于輔助函數χh，因為Πh(u°Φh)∈Vh，且滿足(?(Πh(u°Φh))，ωh)=(?(u°Φh)，ωh)，?ωh∈Vh.所以我們取χh=Πh(u°Φh)，由引理2.2有

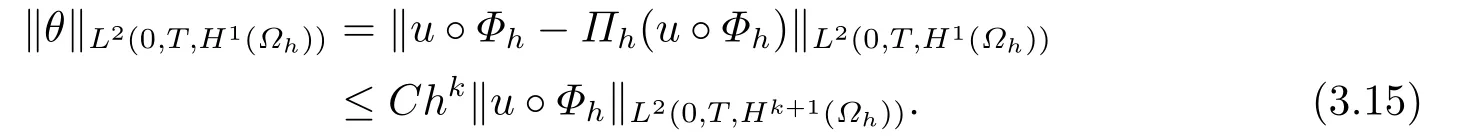
又θt=ut°Φh-Πh(ut°Φh)，類似地有

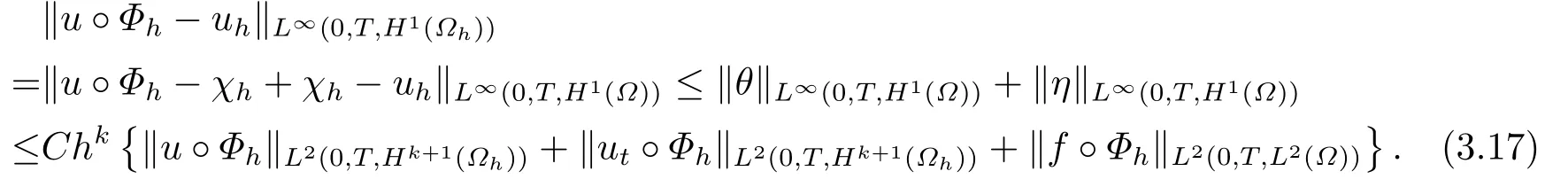
應用引理2.3即可得到(3.4)式，定理證畢.

4.全離散問題的誤差估計

現在我們采用向后歐拉差分格式構造問題(3.1)的全離散格式，目的是求解初邊值問題的真解u(x，t)在節點tn，n=1，2，...N處的近似值.對于[0，T]上的任意光滑函數φ，定義φn=

與問題(3.1)對應的的全離散逼近格式為:求Un∈Vh，n=0，1，...N，使得

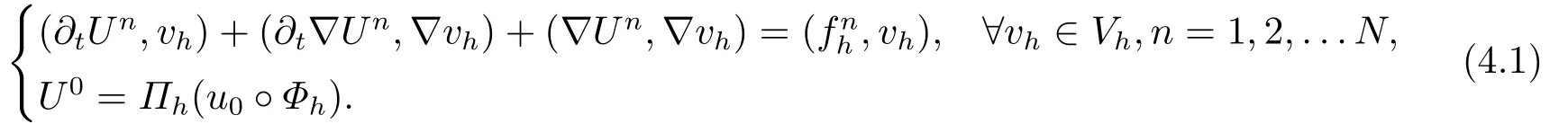
在(3.1)式中令t=tn，可得

定理4.1問題(4.1)有唯一解.

證記則全離散問題(4.1)可以等價的表示為:求Un∈Vh，n=0，1，···N，使得

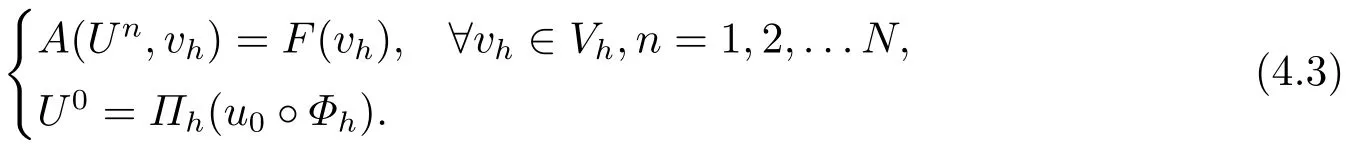
又

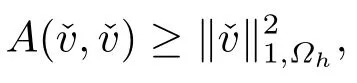
從而A()是Vh上的正定雙線性型，易證A()是Vh上的連續雙線性泛函，而且對于已知的Un－1，F()是Vh上的連續線性泛函.于是由Lax-Milgram定理知，方程(4.3)即問題(4.1)存在唯一的解Un∈Vh，n=0，1，...N.

定理4.2設un和Un是問題(4.2)和問題(4.1)的解，f∈L2(0，T，L2(Ω))，u∈L2(0，T，Hk+1(Ω))，ut∈L2(0，T，Hk+1(Ω))，utt∈L2(0，T，H1(Ω))，并且?u有界，則對任意的1≤n≤N，有如下估計

證此處同樣引入輔助函數使得

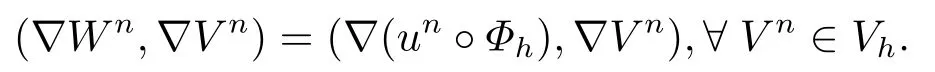
記un°Φh-Un=un°Φh-Wn+Wn-Un=θn+ηn，其中θn=un°Φh-Wn，ηn=Wn-Un.將(4.2)式改寫為

(4.5)式減去(4.1)式，可得

然后，在(4.6)式中令vh=ηn，則有

對于(4.7)式左端，有

同理

結合(4.7)-(4.13)式，可得

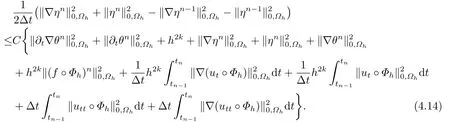
(4.14)式兩端同乘以2Δt，并對n從1到m求和，有

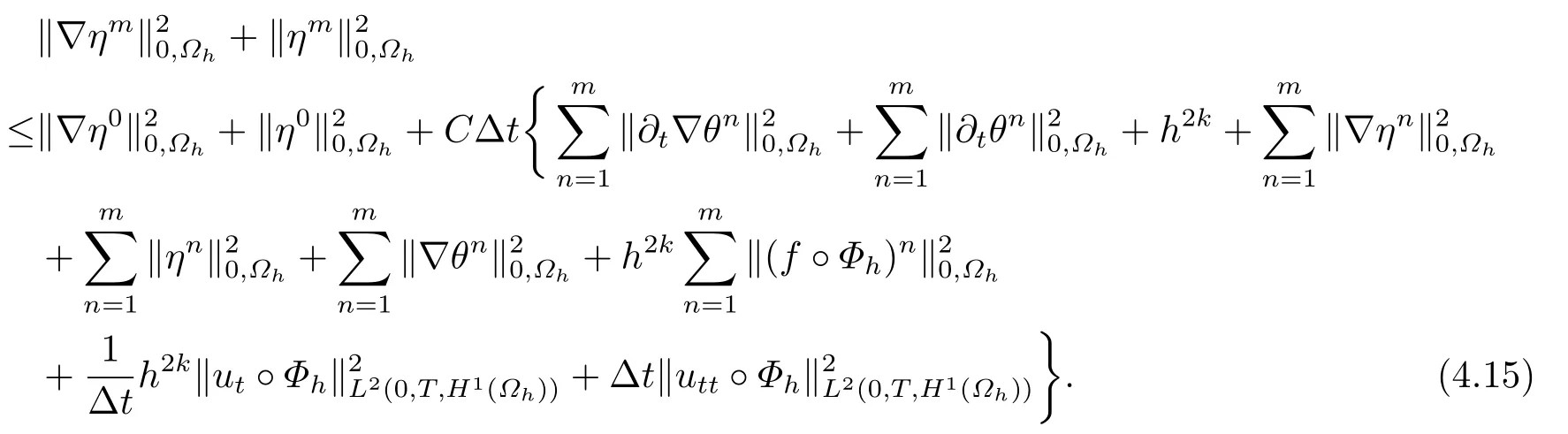
則由離散的Gronwall引理可得

因此

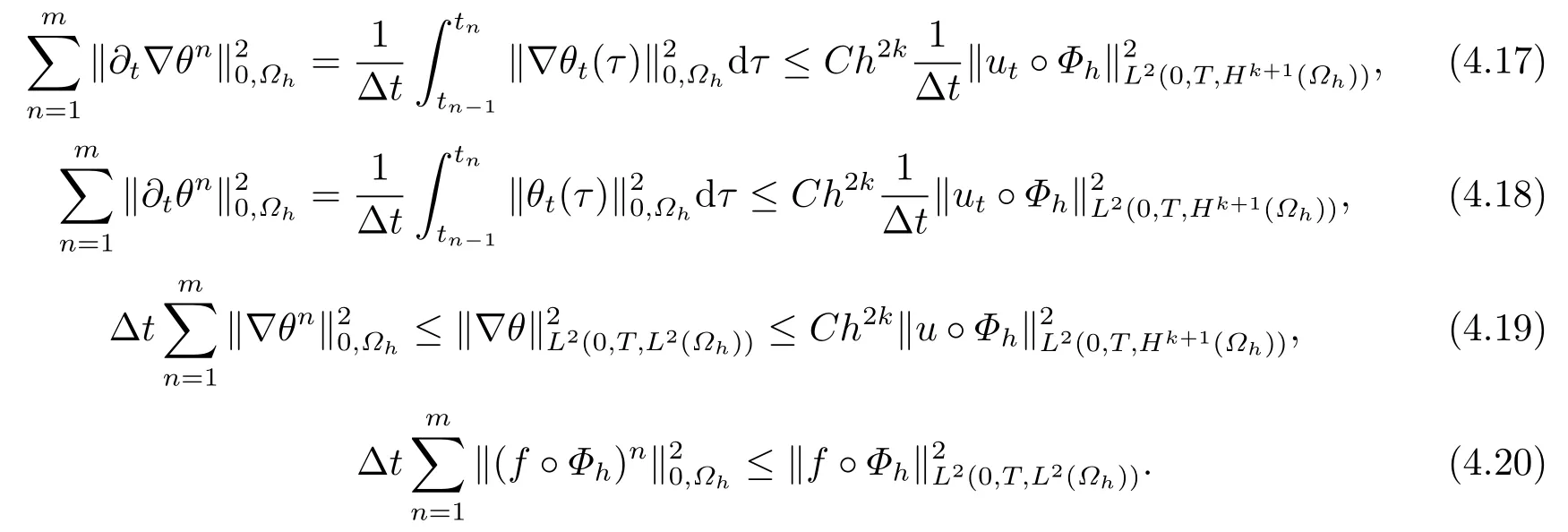
又注意到?η0=η0=0，則結合(4.16)-(4.20)式，對任意的1≤n≤N，有

最后由引理2.3及三角不等式即可得到(4.4)式，定理4.2得證.

5.數值算例

為了驗證理論分析的正確性，我們首先考慮問題(1.1)，其中

可以容易驗證其真解為

然后為了便于數值計算，我們選用二次Lagrange等參元.對空間區域Ω沿x軸和y軸方向剖分成M×M(M=2，4，8，···)份，采用向后歐拉格式對時間區域進行離散，其中如圖5.1所示是一個4×4的二次等參元網格剖分圖.

圖5.1 4×4網格圖

圖5.2和圖5.3分別給出了t=0.1，網格剖分為16×16時問題(1.1)的真解和問題(4.1)的有限元解.表5.1給出了在不同網格剖分下的誤差和收斂階數，從表5.1中可以看出當網格步長h→0時，收斂階為O(h2)，這和我們前面的理論估計是一致的.

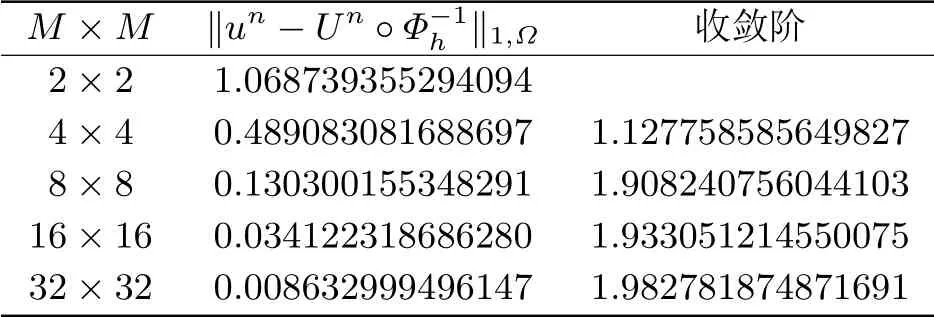
表5.1 t=0.1時的逼近結果

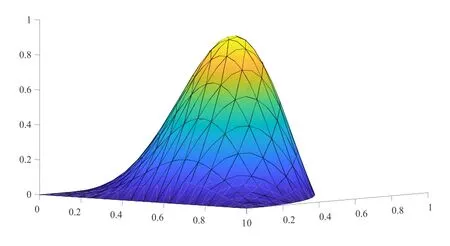
圖5.2 t=0.1時真解u

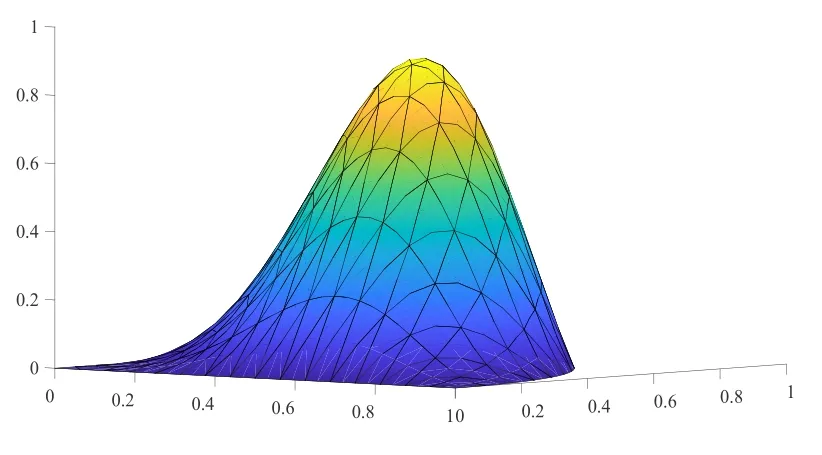
圖5.3 t=0.1時有限元解U