b-距離空間中隱性壓縮不動點定理
王宏穎,賀飛
(內蒙古大學數學科學學院,內蒙古呼和浩特010021)
1.引言
1993年,Czerwik[1]引入了b-距離空間的概念.當空間系數s=1時,該類空間為距離空間,因此b-距離空間是距離空間的推廣.此后許多學者將各種形式的不動點定理建立到b-距離空間中,例如見文[2-4].另一方面,2011年,Berinde等人[5]在距離空間中建立了含有六元連續函數的隱性壓縮不動點定理.之后,有些學者在距離空間討論并發展含有六元函數的壓縮不動點定理的其他形式,例如見文[6-10].最近,Karapinar等人[11]和Aydi等人[12]定義了一類新的函數,并分別在距離空間,四角距離空間下建立了幾類隱性壓縮的不動點定理.
本文在b-距離空間中建立了兩類含有六元連續函數的隱性壓縮不動點定理.第一個結果將Berinde等人[5]的隱性壓縮不動點定理推廣到b-距離空間.應用我們的結果可以推出b-距離空間的Banach型,Chatterjea型,Kannan型壓縮不動點定理.2015年,Dung等人[13]成功解決了Jovanovi等人[14]提出的公開問題,即將b-距離空間中經典Banach壓縮不動點定理的壓縮系數從放寬為[0,1).我們的結果也可以推出Dung等人的結果.第二個結果將距離空間中Karapinar等人[11]提出的新的Kannan型壓縮不動點定理和四角距離空間中Aydi等人[12]提出的新的′Ciri′c-Reich-Rus型壓縮不動點定理建立到b-距離空間,并統一了這兩種類型的壓縮條件.
2.預備知識與主要結果
首先我們來回顧一下b-距離空間一些基本定義和性質.
定義2.1[1]設X是一個非空集合,s≥1是給定的正實數,如果函數d:X×X→[0,∞)滿足以下條件:
(b1)d(x,y)=0,當且僅當x=y;
(b2)d(x,y)=d(y,x);
(b3)d(x,y)≤s[d(x,z)+d(z,y)],
則稱d為X的b-距離,且稱(X,d)為b-距離空間,其中s稱為(X,d)的系數.
顯然,b-距離空間是距離空間的推廣.
定義2.2[1]設(X,d)是系數為s≥1的b-距離空間,{xn}是X中的點列.
1)點列{xn}收斂于x∈X,當且僅當
2)點列{xn}是Cauchy列,當且僅當
3)空間(X,d)是完備,當且僅當X中的任意Cauchy列都收斂.
下面是Suzuki[15]提出的b-距離空間中的一個重要引理.進一步,此引理可以被推廣到類擬b-距離空間中,參見文[16].
引理2.1[15]設(X,d)是系數s≥1的b-距離空間,{xn}?X.如果存在一個r∈[0,1),使得對任意n∈N,滿足
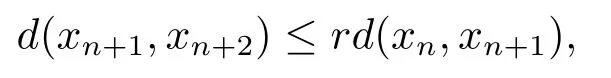
那么{xn}是一個Cauchy列.
下面介紹含有六元函數的隱性壓縮的相關概念.
設F是滿足以下兩個條件的六元實值連續函數F:→R+的集合,
(F1)F關于第五變元是非增的,且對任意s≥1,存在h∈[0,1),滿足
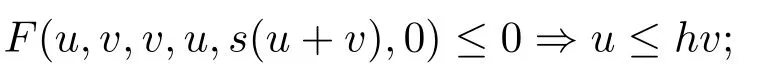
(F2)對任意的u>0,有F(u,u,0,0,u,u)>0.
我們給出一些滿足隱性關系的六元連續函數F的具體例子.
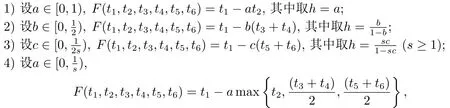
其中取h=max(s≥1);
5)設a∈[0,1),且

6)設a∈[0,
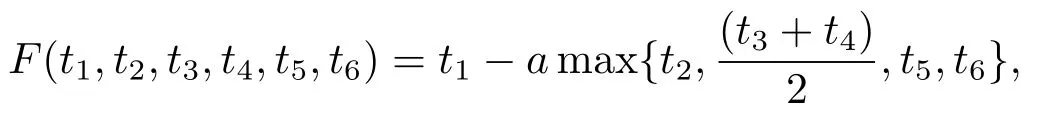
其中取h=(s≥1).
下面例子說明隱性壓縮條件中的(F1)和(F2)是相互獨立的.
本計劃第二天清晨永遠離開秦川,可是現在,艾莉突然想在這里多住幾天。很顯然女人不過將她當成一個試圖混進豪宅的女孩——煮咖啡,煮牛奶,洗刷餐具,洗刷馬桶,拿不菲的薪水,住豪華的房子……然后,趁女主人不注意,與男主人調情或者偷情——艾莉相信這樣的生活對很多年輕并且貧困的女孩極具吸引力。現在她必須讓女人相信她是秦川買來的充氣娃娃——工廠出來的產品,供男人發泄性欲的玩具。她對他們的生活不會造成絲毫影響。
例2.2令a∈[0,1),L≥0.
1)設F(t1,t2,t3,t4,t5,t6)=t1-at2-Lt6.容易證明F滿足(F1),其中取h=a,但當L>1時,F不滿足(F2);
2)設F(t1,t2,t3,t4,t5,t6)=t1-at2-Lt3.容易證明F滿足(F2),但當L>1時,F不滿足(F1).
例2.3設F:R6+→R+,容易驗證下列定義的F同時滿足(F1)和(F2).
1)設λ∈[0,1),α∈(0,1),F(t1,t2,t3,t4,t5,t6)=t1-其中取h=
2)設a∈[0,1),α,β>0,α+β<1,
下面給出本文第一個主要結果.
定理2.1設(X,d)是系數為s的完備b-距離空間.設T是X→X的自映射,且滿足存在F∈F,使得對任意x,y∈X,有
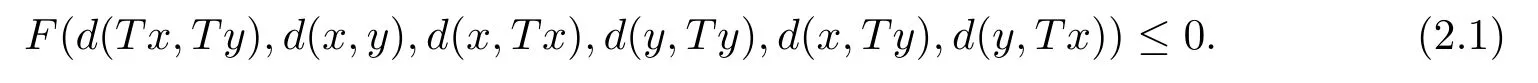
如果d連續或者T連續,那么
(a)T在X中有唯一不動點x*;
(b)由xn+1=Txn,n=0,1,···定義的迭代點列收斂于x*;
(c)當sh<1時,有以下估計成立
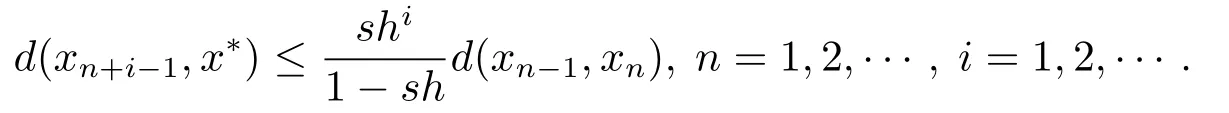
證任取x0∈X,令xn+1=Txn=Tnx0,n=0,1,2,···,由此構造迭代點列{xn}.
第1步證明{xn}是Cauchy列.
由(2.1)式可得
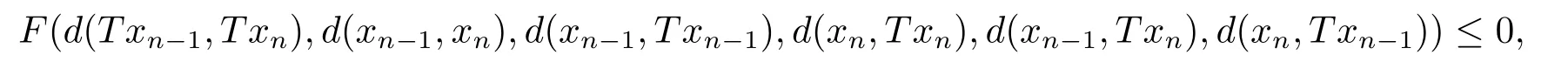
即
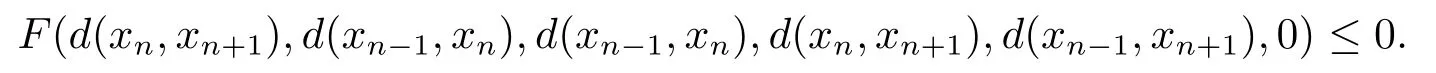
由b-距離空間的三角不等式可得
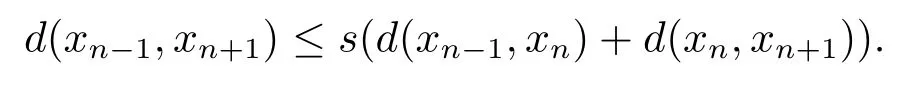
由于F滿足條件(F1)且關于第五變元是非增的,故
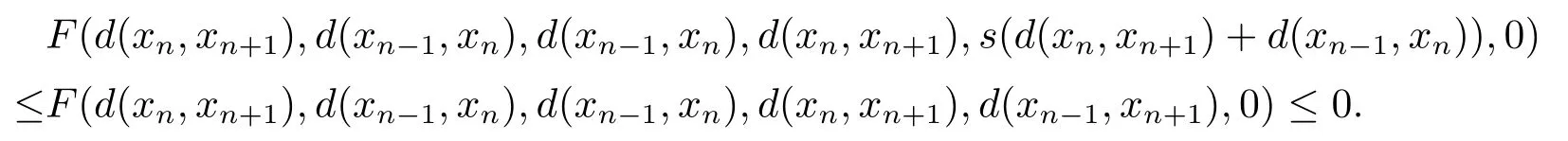
由F滿足條件(F1)可知,存在h∈[0,1),使得

由(2.2)和引理2.1可得,{xn}是X中Cauchy列.又由于X是完備的,故存在x*∈X,使得

此時結論(b)得證.
第2步證明x*為T的不動點.
以下分d連續和T連續兩種情況證明.
情況1若d有連續性.
由(2.1)可得
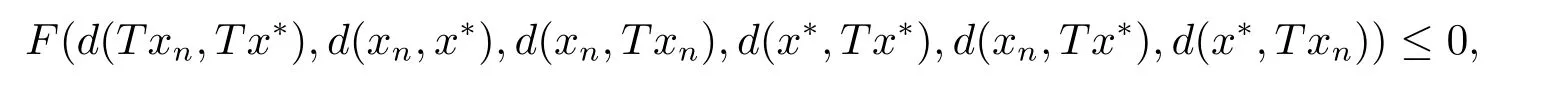
即
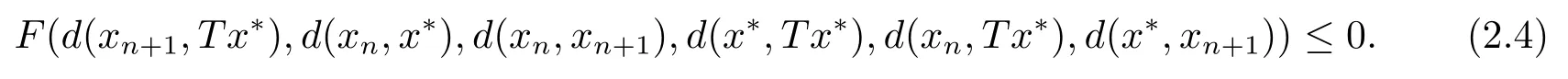
對(2.4)兩邊同時取極限,由F和d的連續性可得
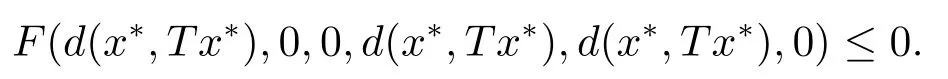
由于F關于第五變元是非增的,故
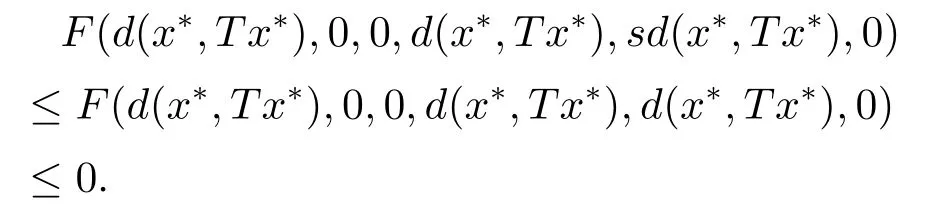
由上式和F滿足條件(F1)可知,存在h∈[0,1),使得d(x*,Tx*)≤h0=0,即x*=Tx*.
情況2若T是連續的.
由(2.3)和T的連續性可得
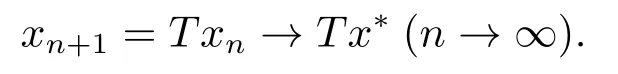
由于極限的唯一性,故x*=Tx*.
第3步證明不動點的唯一性.
反證法,假設T存在另一個不動點y*且x*y*,則d(x*,y*)>0.由(2.1)可得
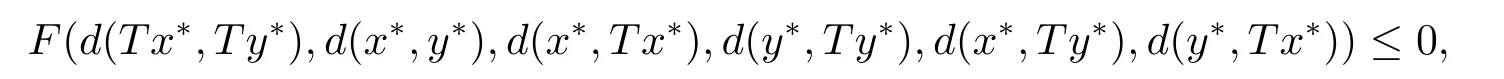
即
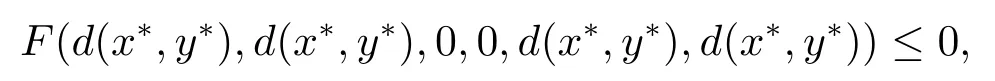
與F滿足條件(F2)矛盾.因此T有唯一的不動點x*.
下證結論(c)成立.
由(2.2)可得
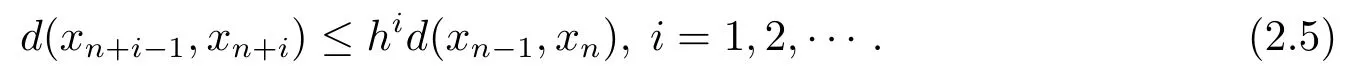
由(2.5)及三角不等式可得
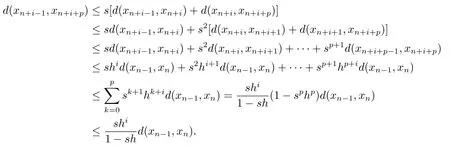
令p→∞時,可得結論(c)成立.
評注2.1當s=1時,定理2.1為Berinde[5]在距離空間下建立的含有六元函數的隱性壓縮不動點定理(文[5]中定理3.3),因此是Berinde結果的推廣.
2018年,Karapinar等人[11]在距離空間中給出了另一類新的壓縮形式的定義,并證明了相關隱性壓縮不動點定理.2019年,Aydi等人[12]在四角距離空間下建立了該類隱性壓縮不動點定理.之后許多學者在不同空間下建立該類型的隱性壓縮不動點定理.下面我們將Karapinar等人和Aydi等人的結果建立到b-距離空間.
定理2.2設(X,d)是系數為s的完備b-距離空間,T是X→X的自映射滿足,存在六元實值連續函數F:R+滿足條件(F1),使得對任意x,y∈XFix{T},有若d連續或者T連續時,則
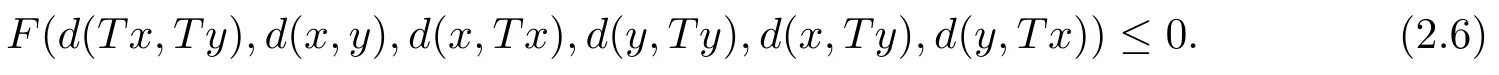
(a)T在X中有不動點x*;
(b)由xn+1=Txn,n=0,1,···定義的迭代點列收斂于x*;
(c)當sh<1時,有以下估計成立
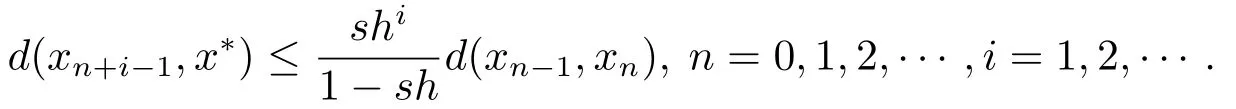
證任取x0∈XFix{T},令xn+1=Txn=Tnx0,n=0,1,2,···,由此構造迭代點列{xn}.不妨假設xnFix{T},n=1,2,3···.
類似于定理2.1的第一步,可以證明{xn}是Cauchy列.由于X是完備的,故存在x*∈X,使得xn→x*(n→∞).下面分兩種情況證明x*是T的不動點.
情況1當d連續時.
反證法,假設x*Tx*,則x*∈XFix{T}.由(2.6)可得
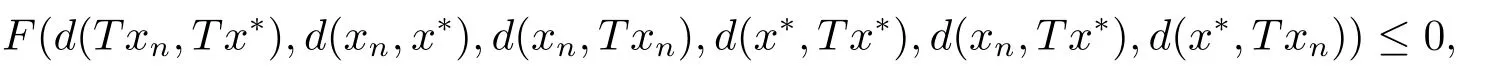
即
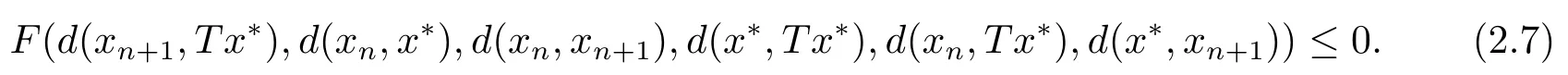
對(2.7)兩邊同時取極限,且由F滿足條件(F1)可得,
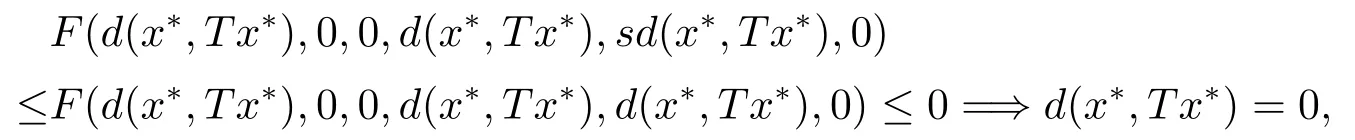
則與x*Tx*產生矛盾.因此x*是T不動點.
情況2當T連續時.
由T連續可得,
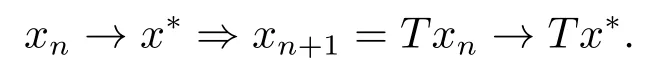
由于極限的唯一性,故x*=Tx*是T的不動點.
結論(b),(c)的證明與定理2.1的證明相同,在此省略.
3.推論
這一部分我們將給出兩個主要定理的推論.
將定理2.1中的F取為例2.1中的1)可得下面的結果.
推論3.1設(X,d)是系數為s的完備b-距離空間,T是X→X的自映射.如果存在λ∈[0,1)滿足,對任意x,y∈X,有d(Tx,Ty)≤λd(x,y),那么T在X中有唯一不動點.
評注3.1注意到推論3.1的條件d(Tx,Ty)≤λd(x,y)可以推出T是連續的.特別地,推論3.1就是文[14]中定理2.1,這個結果解決了Jovanovi′c等人[15]提出的公開問題.
將定理2.1中的F取為例2.1中的2)可得下面的結果.
推論3.2設(X,d)是系數為s的完備b-距離空間.設T是X→X的自映射滿足,存在λ∈對任意x,y∈X,有
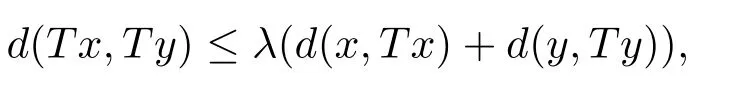
若d連續或者T連續時,則T在X中有唯一不動點.
評注3.2推論3.2是b-距離空間中的Kannan型壓縮不動點定理,且壓縮條件與空間系數s無關.
將定理2.1中的F取為例2.1中的3)可得下面的結果.
推論3.3設(X,d)是系數為s的完備b-距離空間.設T是X→X的自映射滿足,存在λ∈,對任意x,y∈X,有
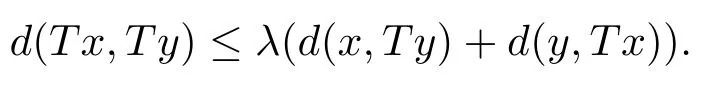
若d連續或者T連續時,則T在X中有唯一不動點.
評注3.3推論3.3是b-距離空間中的Chatterjea型壓縮不動點定理.
將定理2.1中的F取為例2.1中的4)可得下面的結果.
推論3.4設(X,d)是系數為s的完備b-距離空間.設T是X→X的自映射滿足,存在λ∈對任意x,y∈X,有
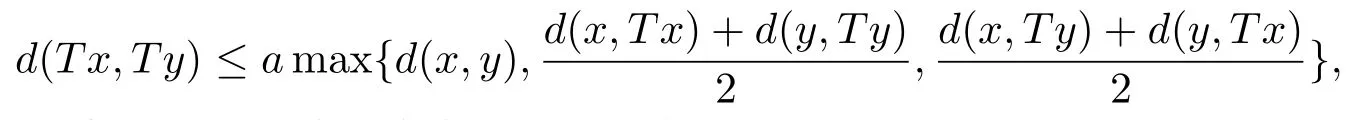
若d連續或者T連續時,則T在X中有唯一不動點.
將定理2.1中的F取為例2.1中的5)可得下面的結果.
推論3.5設(X,d)是系數為s的完備b-距離空間.設T是X→X的自映射滿足,存在λ1∈且對任意x,y∈X,有
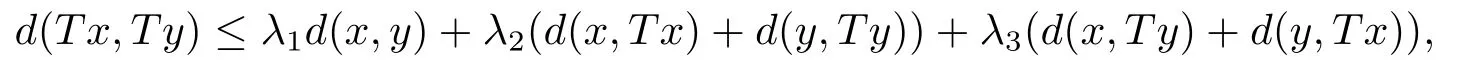
若d連續或者T連續時,則T在X中有唯一不動點.
將定理2.2中的F取為例2.3中的1)可得下面的結果.
推論3.6設(X,d)是系數為s的完備b-距離空間.設T是X→X的自映射滿足,對任意x,y∈XFix{T},有
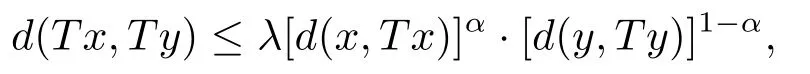
其中λ∈[0,1),α∈(0,1).若d連續或者T連續時,則T在X中有不動點.
評注3.4推論3.6將Karapinar等人[11]提出的新的Kannan型壓縮不動點定理建立到b-距離空間,這是Karapinar等人結果的推廣.
將定理2.2中的F取為例2.3中的2)可得下面的結果.
推論3.7設(X,d)是系數為s的完備b-距離空間.設T是X→X的自映射滿足,對任意的x,y∈XFix{T},有
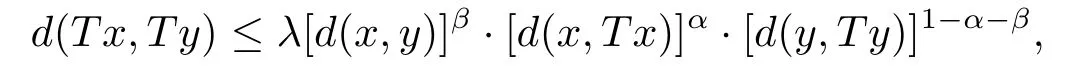
其中λ∈[0,1),α,β>0,且α+β<1.若d連續或者T連續時,則T在X中有不動點.
評注3.5推論3.7將Aydi等人[12]提出的新的′Ciri′c-Reich-Rus型壓縮不動點定理建立到b-距離空間.

