二年級(jí)教學(xué)“乘法分配律”的實(shí)踐與思考

文|吳銳潔

“乘法分配律”的教學(xué)在整個(gè)小學(xué)數(shù)學(xué)教學(xué)中十分重要，承載著重要的數(shù)學(xué)模型，一般安排在中高年段系統(tǒng)學(xué)習(xí)，旨在引導(dǎo)學(xué)生理解運(yùn)算律的意義，使一些運(yùn)算簡(jiǎn)便，提高運(yùn)算能力。然而，通過(guò)訪談我們發(fā)現(xiàn)：學(xué)生對(duì)乘法分配律的掌握情況卻不盡如人意。到底是什么原因?qū)е逻@種情況的出現(xiàn)呢？大量的文獻(xiàn)資料表明：一是模型理解問(wèn)題，學(xué)生著眼于方法的解釋“先求什么再求什么”而非方法間算式的內(nèi)在關(guān)系的闡釋?zhuān)瑢?dǎo)致規(guī)律的機(jī)械記憶而沒(méi)有理解規(guī)律的內(nèi)涵本質(zhì)；二是難點(diǎn)集中問(wèn)題，五個(gè)運(yùn)算律的系統(tǒng)學(xué)習(xí)共同奔著“簡(jiǎn)算”的目的，這種高容量的學(xué)習(xí)方式造成學(xué)生對(duì)抽象的運(yùn)算律的混淆，也導(dǎo)致“乘法分配律”的本質(zhì)意義和價(jià)值得不到充分體現(xiàn)；三是練習(xí)指向問(wèn)題，大量變式練習(xí)的過(guò)早干擾使學(xué)生誤入學(xué)習(xí)乘法分配律就是“為了簡(jiǎn)算”的怪圈，學(xué)生的思維失去了著力點(diǎn)，難以在腦海里將各種“形似而神各異”的習(xí)題轉(zhuǎn)化成具有運(yùn)算律基本結(jié)構(gòu)特點(diǎn)的算式。

能否讓學(xué)生對(duì)“乘法分配律”的認(rèn)知逐步遞加從而分散難點(diǎn)、把握重點(diǎn)呢？查看教學(xué)參考書(shū)，書(shū)中提到運(yùn)算律的學(xué)習(xí)第一階段沒(méi)有出現(xiàn)“乘法分配律”的概念，是自然滲透、自覺(jué)運(yùn)用階段，那我們能不能讓書(shū)中的這個(gè)建議更加顯性化些呢？查看教材，以北師大版為例，二年級(jí)“6～9的乘法口訣”單元中，通過(guò)點(diǎn)子圖、線段圖來(lái)說(shuō)明像“7個(gè)6就是5個(gè)6加2個(gè)6的和”這樣的問(wèn)題，通過(guò)“做乘法表”引導(dǎo)學(xué)生溝通理解口訣之間的內(nèi)在聯(lián)系，探索乘法表規(guī)律，這些已經(jīng)開(kāi)始滲透乘法分配律了；在三年級(jí)學(xué)習(xí)整數(shù)乘法計(jì)算方法的過(guò)程，事實(shí)上也在不斷借助點(diǎn)子圖法、解釋表格法、豎式計(jì)算的步驟體會(huì)基于乘法分配律的計(jì)算道理；此外，在幾何領(lǐng)域，三年級(jí)學(xué)習(xí)長(zhǎng)方形的周長(zhǎng)和面積變化中，也隱含著“乘法分配律”的幾何模型。在正式學(xué)習(xí)“乘法分配律”之前，教材已有多次運(yùn)用乘法分配律解決問(wèn)題。

那么，在保持現(xiàn)有教材體系的基礎(chǔ)上，如果我們?cè)谒哪昙?jí)或三年級(jí)學(xué)習(xí)“乘法分配律”之前做適當(dāng)?shù)臐B透，是不是可以更充分體現(xiàn)“乘法分配律”的本質(zhì)意義和價(jià)值，同時(shí)也使學(xué)生更好地理解和運(yùn)用呢？因此，本研究聚焦到二年級(jí)開(kāi)展“乘法分配律”滲透的“縱向同課異構(gòu)”教學(xué)，以探尋學(xué)生學(xué)習(xí)的可能性。

【教學(xué)過(guò)程】

在教學(xué)“乘法口訣”時(shí)滲透乘法分配律，借助直觀實(shí)物模型抽象成點(diǎn)子圖模型的“分開(kāi)看”與“合并看”——意義的“分開(kāi)說(shuō)”與“合并說(shuō)”——算式的“分開(kāi)算”與“合并算”來(lái)實(shí)施，教學(xué)過(guò)程如下：

一、課前小游戲：分開(kāi)說(shuō)與合并說(shuō)

1.男生好，女生好。（這是分開(kāi)說(shuō)）→男生女生好。（這是合并說(shuō)）

2.我愛(ài)閱讀，我愛(ài)運(yùn)動(dòng)。→我愛(ài)閱讀和運(yùn)動(dòng)。

3.我左手有3袋蘋(píng)果，我右手有4袋蘋(píng)果。→我兩只手一共有（3+4）袋蘋(píng)果。

【設(shè)計(jì)意圖：以生活中“分開(kāi)說(shuō)與合并說(shuō)”的小游戲拉近與學(xué)生的距離，緊密聯(lián)系本節(jié)課乘法分配律“分”與“配”的特征，激活學(xué)生對(duì)乘法分配律的生活經(jīng)驗(yàn)，激發(fā)學(xué)生的學(xué)習(xí)熱情。】

二、圖式對(duì)接：看——說(shuō)——算

1.實(shí)物蘋(píng)果模型，滲透算律。

（1）觀察下面的紅蘋(píng)果和青蘋(píng)果，并根據(jù)圖填空。

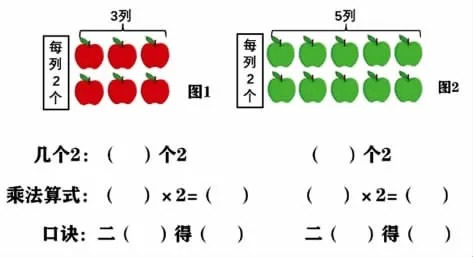
（2）把圖1和圖2合在一起成圖3，請(qǐng)問(wèn)：現(xiàn)在一共有多少個(gè)蘋(píng)果？

追問(wèn)：你是怎么得到16的？8是怎么來(lái)的？有幾個(gè)2？對(duì)應(yīng)的乘法算式怎么寫(xiě)？請(qǐng)你用一句口訣快速計(jì)算。

學(xué)生在充分交流基礎(chǔ)上小結(jié)：3個(gè)2加5個(gè)2得到（3+5）個(gè)2，也就是8個(gè)2，對(duì)應(yīng)的算式是3×2+5×2=（3+5）×2=8×2，可以用口訣“二八十六”快速地得到結(jié)果。

【設(shè)計(jì)意圖：本環(huán)節(jié)從可視化蘋(píng)果實(shí)物圖模型的“分開(kāi)看”出發(fā)走向“合并看”，喚醒學(xué)生乘法意義“幾個(gè)幾”的學(xué)習(xí)經(jīng)驗(yàn)，生成教學(xué)所需，初建模式。通過(guò)直觀性的模型圖使學(xué)生建立圖式對(duì)接，積累可視性學(xué)習(xí)經(jīng)驗(yàn)，滲透乘法分配律。】

2.對(duì)比延伸模型，豐富算律。

（1）仔細(xì)觀察下面的蘋(píng)果圖，看圖寫(xiě)出幾個(gè)幾、列出算式并寫(xiě)出口訣。

（2）這兩幅圖有什么聯(lián)系，你是怎么想的？

請(qǐng)你結(jié)合“幾個(gè)幾+幾個(gè)幾”來(lái)解釋說(shuō)明，并用一個(gè)等式來(lái)表示它們之間的關(guān)系。

【設(shè)計(jì)意圖：本環(huán)節(jié)既是對(duì)上一環(huán)節(jié)的鞏固，也是對(duì)上一環(huán)節(jié)的延伸，學(xué)生在對(duì)比觀察中發(fā)現(xiàn)，有的可以豎著合并，有的可以橫著合并，這樣的設(shè)計(jì)讓教學(xué)內(nèi)容更具寬度。】

3.抽象點(diǎn)子模型，明晰算律。

請(qǐng)你仔細(xì)觀察，蘋(píng)果抽象笑臉，笑臉抽象點(diǎn)子圖，這幾幅圖有什么區(qū)別？

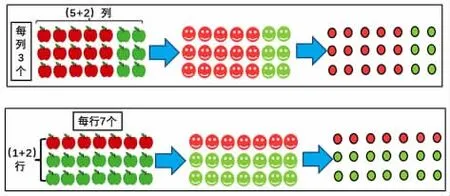
【設(shè)計(jì)意圖：本環(huán)節(jié)通過(guò)實(shí)物模型的動(dòng)態(tài)變化，直觀形象，過(guò)渡到點(diǎn)子圖這一半抽象模型的呈現(xiàn)，讓學(xué)生在對(duì)比中厘清不同模型圖本質(zhì)上是一致的，從而在腦海中建立起多元化又相互關(guān)聯(lián)的模型表征，有效積累表象操作，為后續(xù)轉(zhuǎn)向符號(hào)操作的學(xué)習(xí)打好基礎(chǔ)。】

4.選擇模型，深化算律。

（1）請(qǐng)你在圖1、2、3中選擇兩幅圖，使它們合并在一起后能用類(lèi)似3×2+5×2=（3+5）×2=8×2的算式表示。

（2）為什么你不選擇圖2和圖3合并在一起？

（3）圖1和圖3一定能拼成功嗎？

【設(shè)計(jì)意圖：本環(huán)節(jié)直接選用點(diǎn)子圖讓學(xué)生尋找可合并的模式，關(guān)注學(xué)生基本活動(dòng)經(jīng)驗(yàn)積累的學(xué)習(xí)，學(xué)生在合并擺的過(guò)程中逐步明晰模型特征。同時(shí)，以反例沖擊，為歸納算律埋下伏筆，讓教學(xué)內(nèi)容更具深度。】

5.歸納小結(jié)，表達(dá)算律。

觀察算式，你發(fā)現(xiàn)了什么？?jī)蓚€(gè)分開(kāi)算的算式，怎樣才能拼成一個(gè)乘法算式呢？

學(xué)生觀察算式特點(diǎn)交流后小結(jié)：兩個(gè)分開(kāi)算的乘法算式，如果有一個(gè)相同的乘數(shù)，可以合并成一個(gè)乘法算式。

【設(shè)計(jì)意圖：在經(jīng)歷知識(shí)的形成和發(fā)展過(guò)程后，自主觀察發(fā)現(xiàn)算式的特征，采用不完全歸納法小結(jié)，并學(xué)會(huì)用自己的語(yǔ)言表達(dá)算律，將內(nèi)在思維活動(dòng)外顯出來(lái)，提高探索數(shù)學(xué)問(wèn)題的興趣。】

6.練習(xí)鞏固，應(yīng)用算律。

請(qǐng)你用一句口訣算出下面的算式。

5×7+4×7= 口訣：_______________

9×5+9×2= 口訣：_______________

【設(shè)計(jì)意圖：兩道簡(jiǎn)單的練習(xí)對(duì)接乘法口訣，探究口訣的內(nèi)在聯(lián)系，從乘法意義角度加深對(duì)口訣的理解。】

三、全課小結(jié)，課后延伸

1.今天我們通過(guò)模型圖學(xué)習(xí)了分開(kāi)算與合并算，你學(xué)會(huì)了什么？

2.請(qǐng)根據(jù)點(diǎn)子圖填空。

（1）這是一幅5行9列的點(diǎn)子圖，你可以橫著或豎著圈一圈，把它分開(kāi)來(lái)研究，并分別寫(xiě)出幾個(gè)幾、列出算式和寫(xiě)出口訣（可以借助框圖幫助理解）。

（2）你發(fā)現(xiàn)了什么？

歸納：一個(gè)乘法算式，可以分開(kāi)成兩個(gè)乘法算式再相加，這三個(gè)算式中都有一個(gè)相同的數(shù)。

（3）請(qǐng)你運(yùn)用“分開(kāi)算與合并算”的方法計(jì)算下列算式，說(shuō)說(shuō)你的思考過(guò)程。

（9+7）×3= 18×4=

【設(shè)計(jì)意圖：回顧整理“分開(kāi)→合并”的學(xué)習(xí)過(guò)程，同時(shí)以開(kāi)放式問(wèn)題的設(shè)計(jì)進(jìn)一步深化由“分開(kāi)→合并”的過(guò)程轉(zhuǎn)向“合并→分開(kāi)”的過(guò)程，打破學(xué)生的思維定勢(shì)，拓展學(xué)生自主探究的能力，完善對(duì)所學(xué)內(nèi)容的理解。】

【分析與思考】

這樣的教學(xué)，教學(xué)效果如何呢？我們針對(duì)“學(xué)生能根據(jù)算式特點(diǎn)用乘法分配律對(duì)合并型和分開(kāi)型算式進(jìn)行計(jì)算嗎”做了前測(cè)和后測(cè)，情況如下：

合并型:前測(cè)中正確率達(dá)到69.05%，可以看出盡管學(xué)生沒(méi)有乘法分配律的滲透，但是類(lèi)似于這種題目的解決還是不錯(cuò)的，訪談9人，有1人根據(jù)數(shù)字特點(diǎn)進(jìn)行選擇，其余8人都是先乘后加得出結(jié)果再選擇。后測(cè)中正確率是90.05%，提高了21%，訪談18人，有12人已經(jīng)能直接用乘法分配律合并算，超過(guò)66.7%的學(xué)生能靈活應(yīng)用乘法分配律進(jìn)行解答。

分開(kāi)型：正確率從前測(cè)的35.71%提升到后測(cè)的51.2%，訪談中發(fā)現(xiàn)，前測(cè)中學(xué)生大致有兩種做法：一是拆數(shù)法，將13拆成10和3或9和4再分別乘3；二是乘法意義法：3個(gè)13相加或13個(gè)3先算三九二十七，再連續(xù)加4個(gè)3。后測(cè)中情況有好轉(zhuǎn)，這部分學(xué)生幾乎都用拆數(shù)法結(jié)合乘法意義來(lái)解釋?zhuān)簿褪腔顚W(xué)活用“乘法分配律”進(jìn)行解題。

我們?cè)谒伎迹喝绻o二年級(jí)學(xué)生滲透“乘法分配律”這一內(nèi)容，有何獨(dú)特的價(jià)值？經(jīng)過(guò)實(shí)踐，我們認(rèn)為有以下三點(diǎn)：

1.積累了學(xué)習(xí)乘法分配律的基本活動(dòng)經(jīng)驗(yàn)。

借助不同的模型讓學(xué)生在不同年級(jí)多元滲透乘法分配律的意義，從已有的模型如點(diǎn)子圖、線段圖、面積模型等喚醒學(xué)生對(duì)知識(shí)的直觀理解，積累直觀的操作活動(dòng)體驗(yàn)，讓學(xué)生學(xué)得清楚，悟得明白。

2.助力學(xué)生對(duì)口訣及乘法豎式等的深度理解。

查看教材，二三年級(jí)學(xué)習(xí)了乘法口訣、乘法豎式、長(zhǎng)方形周長(zhǎng)及面積變化中都隱含著乘法分配律。如果在二年級(jí)學(xué)習(xí)乘法口訣時(shí)滲透乘法分配律分與合的意識(shí)，溝通知識(shí)之間的關(guān)聯(lián)性，一方面探究了口訣之間的內(nèi)在聯(lián)系，使口訣的記憶不再割裂，將相鄰或不同口訣之間進(jìn)行鏈?zhǔn)接洃洠涣硪环矫婕訌?qiáng)了學(xué)生對(duì)多位數(shù)乘法豎式算理的深度理解。

3.逐步感知，分散學(xué)習(xí)難點(diǎn)。

“乘法分配律”為何成為學(xué)生的“負(fù)擔(dān)”？原因之一是難點(diǎn)集中，讓“乘法分配律”在不同年級(jí)“小步子”螺旋式循序呈現(xiàn)，初識(shí)“乘法分配律”淡化其簡(jiǎn)算的痕跡，避免各種變式訓(xùn)練過(guò)早地把學(xué)生的視線引向簡(jiǎn)算從而導(dǎo)致各種混淆和模糊不清，加深學(xué)生對(duì)“乘法分配律”的多維度理解，尤其是意義理解，分散其學(xué)習(xí)難點(diǎn)，保證學(xué)習(xí)內(nèi)容的連續(xù)性，使學(xué)生逐步掌握。

通過(guò)教學(xué)實(shí)踐研究，我們認(rèn)為在二年級(jí)學(xué)習(xí)乘法口訣時(shí)注重知識(shí)的整體性，有意識(shí)地滲透乘法分配律是有可能的。如果學(xué)習(xí)乘法口訣時(shí)只是一味地讓學(xué)生花更多的時(shí)間來(lái)背口訣，而非從乘法意義上探究口訣的內(nèi)在聯(lián)系，將導(dǎo)致高年級(jí)學(xué)生對(duì)乘法分配律的學(xué)習(xí)與理解出現(xiàn)障礙。