基于粒子群算法的平面雙道噴涂軌跡規劃研究

藺夢圓，唐倩，李戈，羅育洋，李燚，范秋壘，楊愛平，張鵬輝

（1.重慶大學 機械傳動國家重點實驗室，重慶400044；2.中國船舶重工集團 長江科技有限公司，重慶404130）

0 引言

隨著國家科技的不斷進步與發展，表面噴涂技術在現代工業中的應用更加廣泛，專用的噴涂機器人逐漸代替了人工，因此對于工業機器人如何進行較高質量的軌跡規劃、調節工藝參數，進而提高機器人的噴涂質量日漸成為噴涂領域的重要研究課題。目前對于噴涂機器人的軌跡規劃方法主要由人工示教法和自動軌跡規劃法兩種主要方式構成[1]。人工示教法較為簡單，但調試過程比較繁瑣，同時效果好壞很大程度上取決于操作人員的專業程度，穩定性低，具有很大的不確定性。此外每次工作前都需要再次進行示教操作，制約了噴涂工作的順利開展[2]。自動軌跡規劃方法則以噴涂機器人的噴涂模型、噴涂物體模型為基礎，遵循一定的約束條件和優化準則，實現軌跡規劃目的。自動軌跡規劃法能夠在一定程度上克服人工示教法的弊端，是當前噴涂機器人軌跡規劃的研究熱點問題。

自20世紀90年代以來，已有國內外大量學者對這一熱點問題進行了研究探索。1991年Suk-HwanSuh等[3]基于描述對象的形狀CAD數據，開發了噴涂機器人的軌跡規劃系統；2008年，刁訓娣等[4]提出了可用于求解同一類非線性規劃問題的優化方法；2013年繆東晶等[5]針對空氣噴涂形式，構建用于自由曲面均勻噴涂的軌跡規劃方法，2015年Mayur V.Andulkar[6]針對噴涂機器人在自動曲面上自動噴涂軌跡生成問題，開發了一種集成離線編程方法；2017年Lars Larsen等[7]將路徑規劃與機器學習相結合，利用基于采樣的方法對噴涂機器人的路徑規劃問題進行研究；2017年王國磊等[8]針對當前噴涂速率模型存在的缺點，基于噴涂工藝參數與涂層厚度分布關系研究提出了一種新型的多變量噴涂厚度分布模型。

基于以上內容，不難發現目前的研究偏向于對噴涂模型和規劃系統的構建，但對于噴涂過程中影響噴涂質量的關鍵參數優化研究存在不足。因此，本文采用了粒子群算法與模型相結合的方式對關鍵參數展開優化研究工作。

首先利用橢圓雙β模型對噴涂機器人的噴涂厚度速率模型進行構建，進而得到平面上各點的涂層累積厚度模型，然后通過選擇合適的噴涂路徑規劃方式，并構建實際噴涂厚度與理想噴涂平均厚度關系目標函數，最后利用粒子群算法進行優化求解達到對噴涂機器人自動軌跡規劃的目標。本文的總體框架流程如圖1所示。

1 噴涂模型構建

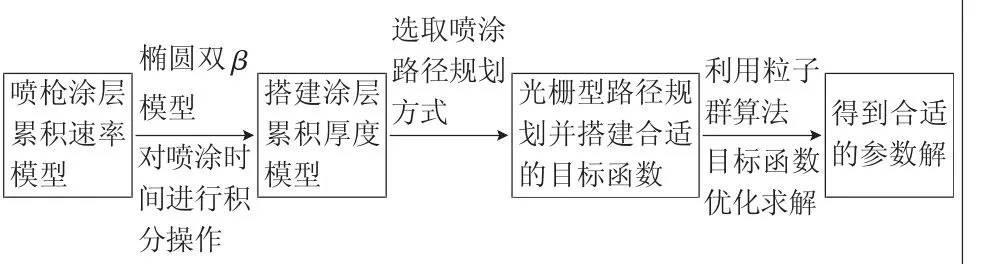
圖1 噴涂軌跡規劃總體框架圖

研究解決噴涂機器人的自動軌跡規劃問題，主要是為了提升噴涂質量，首先需要構建噴涂機器人噴槍涂層厚度累積速率模型，然后在噴涂厚度累積速率模型基礎之上進一步構建準確可靠的噴涂模型。國內外研究人員對于噴涂機器人涂層累積速率模型主要可分為兩類：無限范圍模型和有限范圍模型。其中無線范圍的噴涂模型包含高斯分布模型、柯西分布模型；有限范圍的噴涂模型包含β分布模型、橢圓雙β分布模型、分段函數模型等[5]。基于文中研究的空氣噴涂類型，在多種噴涂模型中，屬于有限范圍模型的橢圓雙β模型更加貼合噴涂機器人實際生產工作環境，應用更為廣泛，更具有研究價值[9]。此外考慮到噴涂涂層的均勻性問題，還將采用雙道噴涂的方式進行相應的噴涂處理[10]。橢圓雙β模型分布如圖2所示。

基于橢圓雙β模型的噴槍空氣噴涂模型，在實際的生產加工過程中，噴涂機器人的噴槍噴霧會附著在噴涂物體的表面形成橢圓形噴涂區域，圖中描述的為放置在距離噴槍h的平面上形成的橢圓形噴涂區域。其中對于噴涂表面上的任意一點P在單位時間內的噴涂累積速率模型函數為[9]

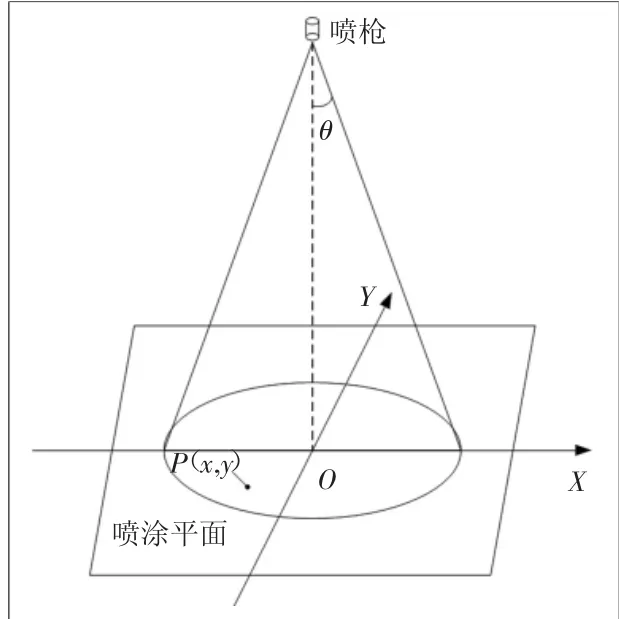
圖2 橢圓雙β模型分布圖

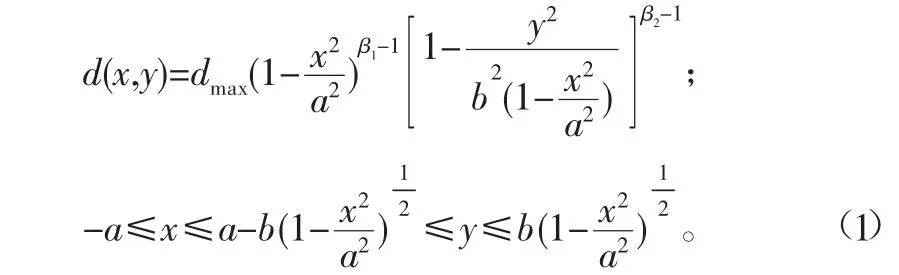
基于橢圓雙β模型的對稱性分布特點，可以選擇從X、Y兩個方向進行路徑規劃過程中噴涂厚度的研究，若研究過程中選擇沿噴涂區域的X軸方向進行噴涂厚度累積模型的研究，在相同的噴槍移動速率條件之下經過模型X軸的時間更長，因此噴涂區域內單位點上累積的噴涂厚度也會增加，進而導致噴涂質量降低[10]。若選擇沿噴涂區域的Y軸方向進行研究，可以有效避免以上問題，同時也更加契合所選算法的研究，因此本文后續內容將通過對Y軸（短軸）方向的涂層速率累積模型進行構建，進而與優化算法相結合開展路徑規劃問題的研究。

式（1）展示了噴涂區域內某一點在單位時間內的厚度累積情況，本文后續研究需要對整個噴涂時間內的噴涂累積厚度模型進行構建，因此在式（1）建立的單位點噴涂累積速率模型之上，需要對噴涂區域內某一單位點在整個噴涂時間內的累積厚度進行計算分析。

噴槍中心點沿Y軸隨時間的移動如圖3所示。在厚度累積模型的構建中，假設噴槍沿Y軸的移動速度為v，則對于噴涂區域內的任意一點P（x0,y0），經過該點的噴涂總時間為ty=2b0(1-x02/a02)1/2/v，進而通過涂層厚度累積速率模型對時間的積分可以得出總時間下噴涂區域內任意一點P的厚度累積模型函數為

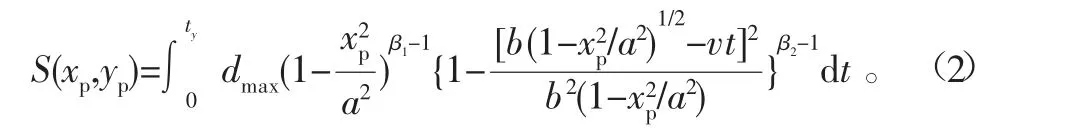
式中：自變量xp隨選取點P的位置變化而變化；v為噴涂機器人的噴槍沿Y軸的移動速率，為可調節變量。

上述過程得到基于橢圓雙β模型的單道噴涂累積速率函數，另外為了保證噴涂厚度的均勻性，還需要對物體進行雙道噴涂處理，并對雙道噴涂厚度累積模型進行構建。雙道噴涂方式過程如圖4所示。

從圖4中可以看出，由于噴涂模型的橢圓形樣式，在雙道噴涂模型的邊界處會存在一定的相交，形成兩次噴涂的形式，因此對于雙道噴涂過程中的噴涂厚度累積函數由3部分組成，具體的函數表達式為：

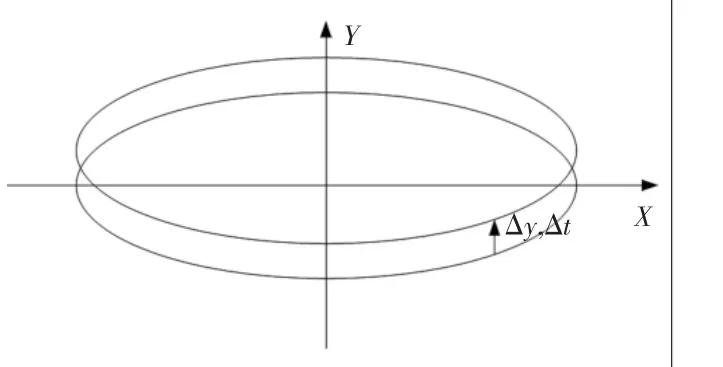
圖3 噴涂軌跡隨時間移動示意圖

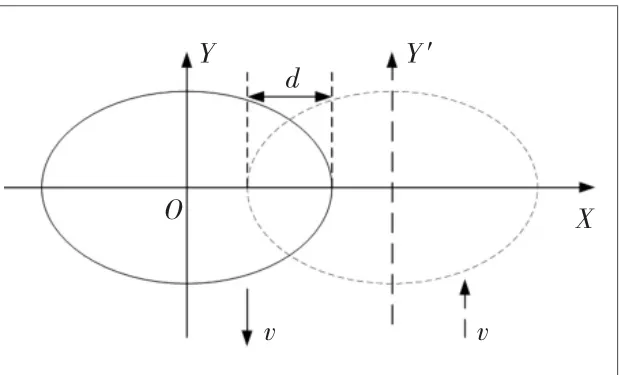
圖4 雙道噴涂過程圖

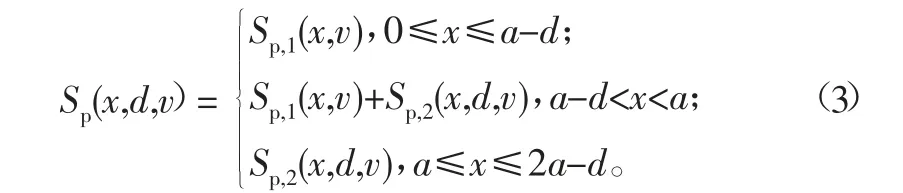
2 噴涂機器人自動軌跡規劃

噴涂機器人的厚度累積模型構建完成后，對噴涂機器人的自動軌跡規劃研究需要解決另外一個問題——噴涂路徑方式的選擇。

選擇合適的噴涂路徑方式與式（3）構建的雙道噴涂厚度累積模型相結合，進而利用優化算法對噴涂過程中的各個參數進行分析求解，能夠獲得較為理想的優化解。

噴涂機器人軌跡規劃研究中存在兩種常用的路徑規劃類型：螺旋形路徑規劃和光柵型路徑規劃[8]。前一規劃方式具有算法簡單、易于操作的優點，但同時存在噴涂邊緣位置噴涂厚度均勻性較差等問題，導致噴涂質量降低。后者雖然在噴涂過程中較容易出現斷點等致命的缺點，但可以保證整體噴涂物體表面具有較為不錯的噴涂質量，同時軌跡規劃的實現算法計算效率高，時間短，效率優于螺旋形路徑規劃方式[10]。因此光柵型的路徑規劃方式應用較為廣泛，適用性更強。在實際的生產過程中需要根據噴涂機器人的類型及噴涂物體平面的表面特征進行選取。根據研究中的實際情況，采用光柵型路徑進行噴涂軌跡規劃，光柵型規劃路徑如圖5所示。

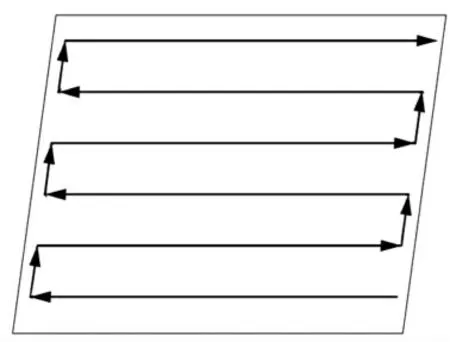
圖5 光柵型路徑規劃示意圖

采用光柵型軌跡規劃方式進行路徑規劃工作，在噴涂機器人噴涂過程中，噴槍噴頭與噴涂物體表面的距離h一般為經驗值，需要根據現場實際的生產操作過程來指定，并且在噴涂過程中保持穩定，在本文的研究過程中，根據式（3）列出的噴涂模型函數表達式，可以得到研究中噴涂厚度很大程度上取決于噴涂機器人的噴嘴移動速度v和雙道噴涂過程中的交叉距離d的結論。

此外對于噴涂效果的評判標準，若僅通過厚度的穩定性來評判噴涂效果，雖然能在一定程度上體現出優化算法的優劣，但存在評判標準不夠全面的問題。因此為了評價噴涂效果的均勻性，研究中多采用厚度方差作為評價函數[11]，進行定量分析，即利用噴涂平面任意一點p（x,y）的實際噴涂厚度Sp與理想噴涂平均厚度SA間的方差作為目標函數，進行涂層厚度效果的鑒別，具體的目標函數為

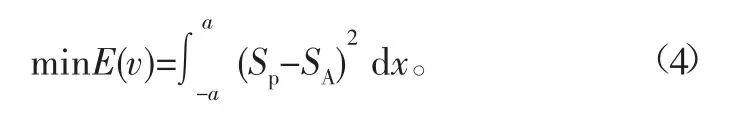
式中：SA為理想噴涂平均厚度，經驗值一般選取50 μm；積分上下限分別為橢圓雙β模型中的長軸兩坐標點的x軸坐標值。

噴涂機器人的軌跡規劃問題涉及的目標函數較為復雜，如果基于單純的普通的計算方法求解最優解，費時費力，同時求出的解可能也存在缺陷，無法達到優良的效果。因此本文結合課題組自主研發的六自由度噴涂機器人、重慶長江涂裝廠生產的ZPQ9型噴槍及現場的生產工作環境之后，采用了改進的粒子群算法進行迭代優化求解。

粒子群算法即PSO算法，是一種進化計算技術，屬于進化算法的一種。這種算法具有實現容易、精度較高、收斂較快的優點[12]。

該算法求解優化過程中首先利用群體，智能建立一個簡化模型，然后從隨機解的角度出發，通過迭代尋找最優解的同時，也通過計算適應度的值評價解的質量，此外還可以利用維度模擬粒子的方向，對當前粒子的多個方向進行多次計算，利用多次重復計算方法實現對多個方向優化求解。粒子群算法整體實現流程如圖6所示。

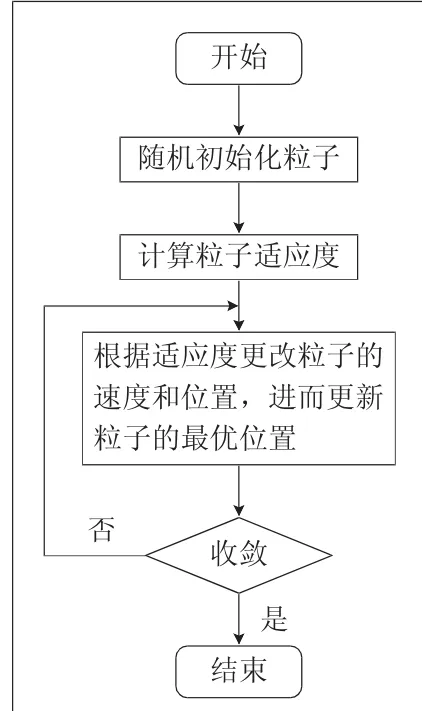
圖6 粒子群算法實現流程圖

3 噴涂實驗結果分析

利用粒子群算法求解中的具體參數選擇及優化求解過程如下。

1） 涂層累積模型參數選擇。根據實際的生產環境和生產設備，基于式（3）列舉的雙道噴涂函數模型，β1與β2為經驗系數，需要根據實際的生產環境決定，對于本文研究中采用的噴涂機器人，β1=2.331，β2=3.000，此外對于a、b、dmax三個參數，也將根據噴涂機器人現場調試的實際效果確定，在本文中將采用a=100.668 mm，b=30.912 mm，dmax=39.800 μm。

2）標準粒子群算法參數選擇。適應度函數為式（4），在粒子群算法的主函數中，慣性權重w=1.000，學習因子c1=c2=2.000，調整迭代速度Ω=1.400，粒子個數size=20.000，迭代次數iternum=500.000，粒子的左極端位置xmin=-100.680，粒子的右極端位置xmax=100.680，粒子的最大速度Vmax=0.500。

3）計算最優解。將目標函數融合到已經設計好的粒子群算法程序中，便可得到優化結果。

通過粒子群算法優化求解后可以得到目標函數在執行500代之后優化求解過程結束，根據程序輸出結果得到粒子群算法優化最終解為：噴涂速度v=26.107 mm/s，d=90.450 mm。

在此參數條件下， 利用Matplotlib 對長軸方向上的涂層累積厚度進行計算仿真，圖7描述了斷面輪廓上的涂層厚度值。

最后選取0～120 mm范圍內粒子群算法優化結果得到的斷面輪廓噴涂厚度與遺傳算法得到的斷面輪廓噴涂厚度進行對比。進而評判粒子群算法進行噴涂軌跡規劃的可靠性和適用性。

兩種優化算法處理下噴涂平面各個位置的涂層厚度對比如圖8所示，其中實線為粒子群算法優化結果，點劃線為遺傳算法優化結果。從圖中可以看出基于粒子群算法優化求解得到的結果，在0～120 mm區間內的涂層厚度最大值為51.550 μm，厚度最小值為48.730 μm，極差為2.820 μm，與理想噴涂厚度之間的方差值為1.280，而遺傳算法得到的區域內涂層厚度最大值為52.530 μm，最小值為48.900 μm，極差為3.630 μm，與理想噴涂厚度之間的方差為1.501，噴涂質量有較為明顯改善，可以達到預期的效果，符合物體表面噴涂要求。

圖7 粒子群算法優化噴涂厚度示意圖

4 結語

本文將雙道噴涂軌跡規劃模型與粒子群算法相結合，對噴涂機器人的自動軌跡規劃問題進行了研究，以提升噴涂機器人的噴涂質量。首先，通過橢圓雙β模型構建雙道噴涂厚度累積模型，采用光柵型規劃路徑，與粒子群算法相結合，以噴涂厚度作為優化目標，對目標函數中的關鍵變量進行優化求解，然后通過對兩種不同優化算法的噴涂厚度結果進行對比分析，最終得到了粒子群算法可以提高噴涂機器人噴涂質量的結論，對于噴涂生產過程具有一定的指導意義及應用價值。

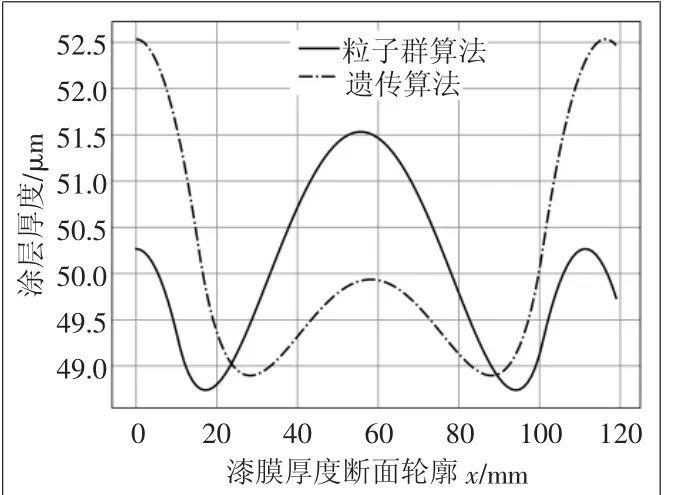
圖8 噴涂厚度對比圖