一道三角形周長最值高考試題的探究與方法應(yīng)用

北京市第十二中學高中部(100071) 趙 毅 劉 剛

1 試題

題目(2020年高考全國Ⅱ卷理科第17 題)?ABC中,sin2A ?sin2B ?sin2C=sinBsinC.

(1)求A;

(2)若BC=3,求?ABC周長的最大值.

試題考查了正(余)弦定理、三角函數(shù)的兩角和與差公式、三角函數(shù)的性質(zhì)、均值不等式等知識,考查了數(shù)學運算、邏輯推理等核心素養(yǎng),檢驗了學生分析問題與解決問題的能力,體現(xiàn)了在知識交匯處命題的特點.試題構(gòu)思巧妙,解法多樣,給考生提供了施展才能的舞臺,為今后的復(fù)習備考指明了方向.

2 解法探究

(1)的解法1因為sin2A ?sin2B ?sin2C=sinBsinC,

(1)的解法2由sin2A?sin2B ?sin2C=sinBsinC,結(jié)合正弦定理,得a2?b2?c2=bc,即b2+c2?a2=?bc.由余弦定理,得cosA=因為0< A < π,所以A=

點評在解三角形中,求角問題通常要轉(zhuǎn)化為求這個角的一個函數(shù)值.解法1 立足于角,通過三角恒等變換求解;解法2 先借助正弦定理將已知等式轉(zhuǎn)化為邊,然后運用余弦定理求解,兩種方法各有特色,體現(xiàn)了轉(zhuǎn)化的數(shù)學思想.

(2)的解法1由正弦定理,得所以所以

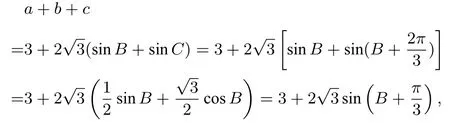
(2)的解法3如圖1,延長BA至D,使得AD=AC,連接CD,則AB+AC=BD.由A=所以D=作?BCD的外接圓O,因為BC= 3,所以點D在優(yōu)弧上運動(不包括端點),當BD過圓心O時(此時A與O重合),BD最大(這是因為圓中弦為直徑時弦長最長),所以(BD)max=故?ABC周長的最大值為

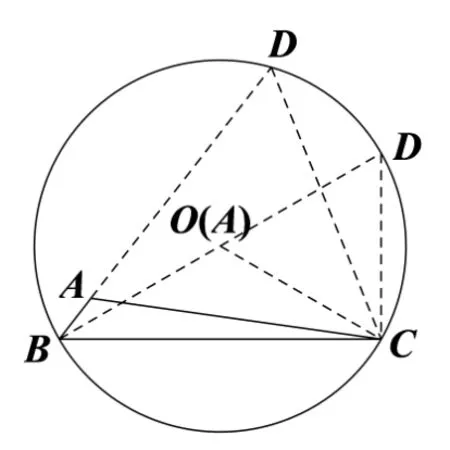
圖1

點評解法1 先借助正弦定理,把邊轉(zhuǎn)化為三角函數(shù),接下來根據(jù)誘導(dǎo)公式、兩角和公式進一步轉(zhuǎn)化為一個三角函數(shù),最后借助三角函數(shù)的有界性求得最值;解法2 從邊入手,根據(jù)均值不等式求得最值;解法3 通過添加輔助線,借助平面幾何知識求解,體現(xiàn)了過程的簡潔性與問題的本質(zhì).以上三種方法是處理解三角形中最值問題的常用方法,在應(yīng)用時,應(yīng)具體問題具體分析,靈活選用.

對本道試題進行一般化探究,得到:

性質(zhì)在?ABC中,角A、B、C的對邊分別為a、b、c,記a=m,A=α,則

(1)?ABC的周長有最大值為

(2)?ABC的面積有最大值為

3 方法應(yīng)用

策略一 借助三角函數(shù)的有界性

例1(2018年全國高中數(shù)學聯(lián)賽江蘇復(fù)賽)在?ABC中,AB= 2AC,且其面積S?ABC= 1,則BC的最小值是____.

解設(shè)?ABC的內(nèi)角A、B、C的對邊分別為a、b、c,則c= 2b,S?ABC== 1,所以b2=由余弦定理,得a2=b2+c2?2bccosA= (5?4 cosA)b2=即4 cosA+a2sinA= 5,所以=5(其中銳角φ滿足sinφ=由此得解得當且僅當cosA=時等號成立,故BC的最小值是

例2(2013年全國高中數(shù)學聯(lián)賽吉林預(yù)賽)已知a、b、c分別為?ABC三個內(nèi)角A、B、C的對邊,bcosC+a ?c=0.

(1)求證A、B、C成等差數(shù)列;(2)若b=求2a+c的最大值.

解(1)因為bcosC+?a ?c= 0,由正弦定理得到sinBcosC+?sinA ?sinC= 0,即sinBcosC+?sin(B+C)?sinC=0,由此得?cosBsinC ?sinC=0.因為00,所以?cosB ?1 = 0,于 是又0< B < π,所以B=又A+B+C=π,所以A+C== 2B,故A、B、C成等差數(shù)列.

策略二 借助均值不等式

例3(第三十屆“希望杯”高二年級一試)在銳角?ABC中,cosA=則tanBtanC的最小值為____.

解由已知可得tanA=所以tan(B+C) =即

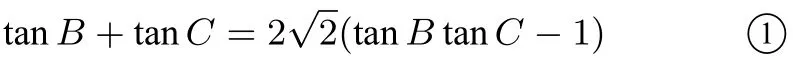
因為?ABC為銳角三角形,所以tanB >0,tanC >0,所 以tanB+ tanC≤所以①變?yōu)閮蛇吰椒?整理得2(tanBtanC)2?5 tanBtanC+2 ≤0,解得tanBtanC≤2,當且僅當tanB= tanC=時等號成立,故tanBtanC有最小值為2.

例4(2017年全國高中數(shù)學聯(lián)賽一試) 在?ABC中,M是邊BC的中點,N是線段BM的中點.若∠A=?ABC的面積為的最小值為____.

解由已知,得所以

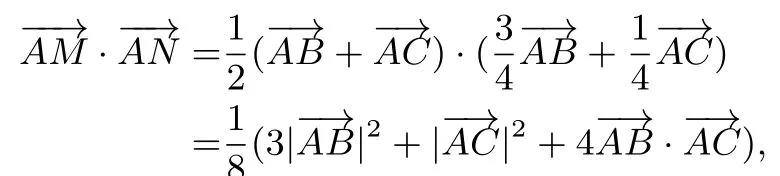
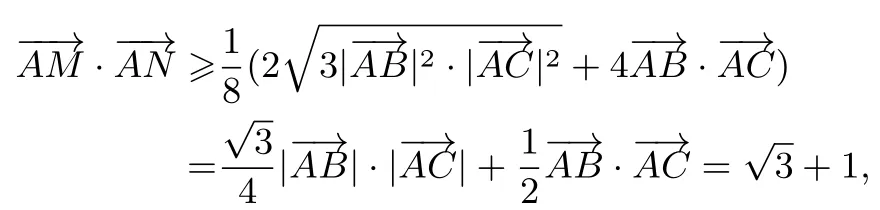
策略三 借助平面幾何知識

例5(2018年北京市中學生數(shù)學競賽)一個三角形的一邊長為8,面積為12,則這個三角形的周長的最小值為____.

解如圖2,在?ABC中,設(shè)BC= 8,BC邊上的高 為h,則×8× h= 12,解得h= 3.在BC的一側(cè)作直線l//BC且與BC的距離為3,以l為對稱軸作出點C的對稱點C′,連接BC′,與l交于A′,則?A′BC的周長是最小的.這是因為AB+AC=AB+AC′≤BC′=BA′+A′C′=BA′+A′C,此 時A′B=A′C.過A′作A′D⊥BC于D,則D是BC的中點,所以A′B2=BD2+A′D2=42+32=25,即A′C=A′B=5,因此?ABC周長的最小值為5+5+8=18.

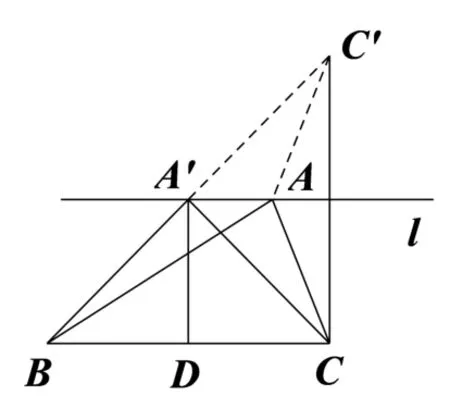
圖2

例6在?ABC中,角A、B、C的對邊分別為a、b、c,已知sinA+sinB=求?ABC面積的最大值.

解如圖3,以線段AB的中點為原點,AB所在直線為x軸建立平面直角坐標系,由c= 2,不妨設(shè)A(?1,0),B(1,0).又sinA+ sinB=由正弦定理,得a+b=所以點C的軌跡是以A,B為焦點的橢圓(除與x軸交點),于是點C的軌跡方程為= 1(y ?= 0),所以?ABC的面積當且僅當點C在橢圓短軸的端點處時等號成立,故?ABC面積的最大值為

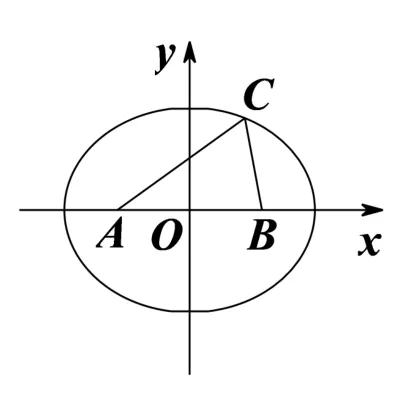
圖3