前緣和轉軸影響翼搖滾特性的數值模擬*

楊小亮，黃世林，楊 起，柴振霞，孫喜萬，劉 偉

(1. 國防科技大學 空天科學學院， 湖南 長沙 410073； 2. 中國人民解放軍93108部隊， 黑龍江 齊齊哈爾 161007)

三角翼因結構強度高、可提供非線性渦升力等優點，是現代戰斗機主要采用的機翼構型，其氣動特性受到了學界的普遍關注，尤其是其動態特性密切關系到現代戰斗機大攻角機動飛行的安全[1]。大攻角條件下，三角翼會產生大幅度自維持的翼搖滾現象。雖然早在20世紀中葉，人們就觀察到了翼搖滾現象，但由于其復雜的非線性氣動特性，直到20世紀80年代才陸續出現對三角翼搖滾現象較為系統的試驗研究[2-5]，而耦合求解N-S方程和Euler剛體動力學方程[6-10]完成三角翼搖滾現象的數值模擬則是二十多年來才開始的事情。

準確捕捉位于三角翼背風面的非線性集中渦是數值模擬三角翼繞流時必須解決的問題。近年來，大量文獻在模擬、分析及控制三角翼上渦流特性方面不遺余力[11-15]，進展卓有成效[16]，而數值模擬渦流主導的三角翼搖滾現象則主要集中在捕捉搖滾現象的定性研究。三角翼上集中渦形成和發展具有強非線性，故對三角翼構型及影響因素極為敏感[17]，造成了數值模擬與實驗之間、實驗與實驗之間往往存在明顯的分歧[5]。提升數值模擬和風洞實驗反映翼搖滾現象物理本質的水平，減小數值模擬和實驗差距，必須研究翼搖滾特性的影響因素。前緣構型和滾轉軸安裝位置是實驗研究必須陳述的關鍵細節，且文獻[4-5]表明不同的處理可導致搖滾特性顯著不同。閻超等[18]研究了前緣形狀對三角翼上渦流特性的影響,但對搖滾特性影響的研究則相對較少。本文耦合求解N-S方程和剛體動力學方程，針對80°后掠三角翼研究前緣構型和轉軸安裝位置影響三角翼搖滾特性的程度和規律。

1 模型及計算方法

1.1 三角翼模型及網格

研究采用80°后掠尖前緣平板三角翼模型，前緣分別采用下削尖、雙面削尖、上削尖三種方式，削尖角均為45°，尾緣不做削尖處理，垂直翼面，如圖1所示。為研究滾轉軸對細長三角翼搖滾特性的影響，基于下削尖前緣三角翼分別研究了滾轉軸安裝在四種不同位置時的搖滾特性，如圖2所示，滾轉軸位置分別安裝在下翼面下方5 mm處(記為Axel_DD)、下翼面上(記為Axel_D)、上翼面上(記為Axel_U)、上翼面上方5 mm處(記為Axel_UU)，四種安裝位置的滾轉軸均位于三角翼體對稱面上。網格生成采用OH型拓撲結構，周向O型、其余方向H型，以平衡描述精度和網格規模[19]。計算網格如圖3所示，網格上游邊界距離三角翼頂點2.5倍根弦長，周向邊界距離體軸2.5倍根弦長，下游邊界距離三角翼尾緣5倍根弦長。網格數為112×226×50(流向×周向×法向)，翼尖、尾緣及翼前緣附近流動較為復雜，局部適當加密。

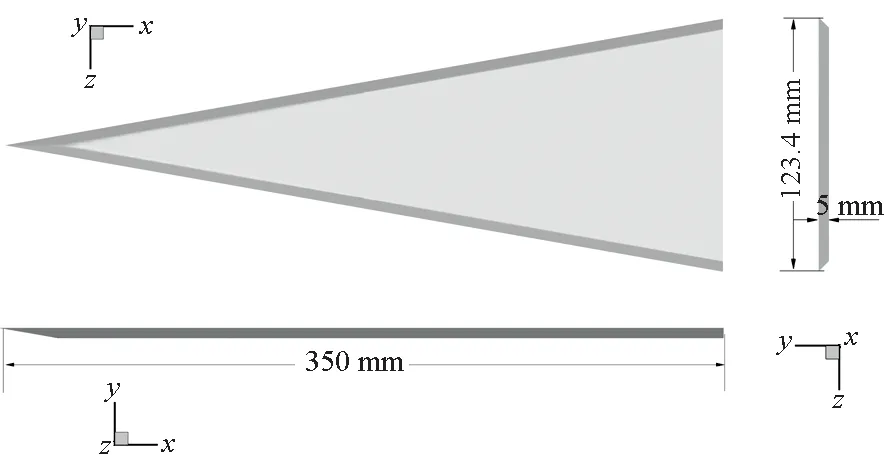
(a) 下削尖前緣(a) Down beveled leading edge

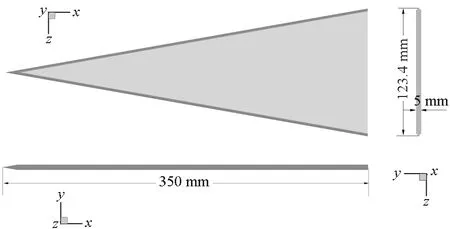
(b) 雙面削尖前緣(b) Double beveled leading edge

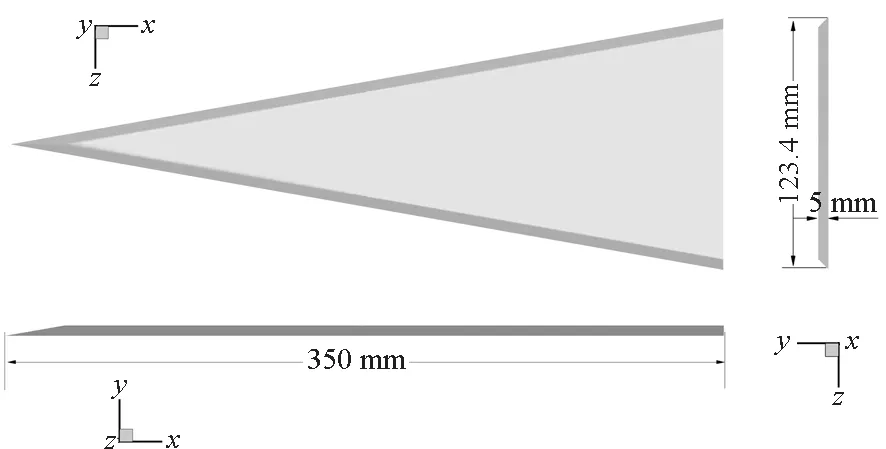
(c) 上削尖前緣(c) Up beveled leading edge圖1 三種不同前緣形狀的80°后掠三角翼模型Fig.1 Three 80° swept delta wing model with different leading edge configuration

(a) 滾轉軸位于下翼面下方(Axel_DD)(a) Roll-axis under the lower wing surface(Axel_DD)

(b) 滾轉軸位于下翼面(Axel_D)(b) Roll-axis on the lower wing surface(Axel_D)

(c) 滾轉軸位于上翼面(Axel_U)(c) Roll-axis on the upper wing surface(Axel_U)

(d)滾轉軸位于上翼面上方(Axel_UU)(d) Roll-axis above the upper wing surface(Axel_UU)圖2 四種不同滾轉軸位置示意圖Fig.2 Schema of four roll-axis installation of delta wing

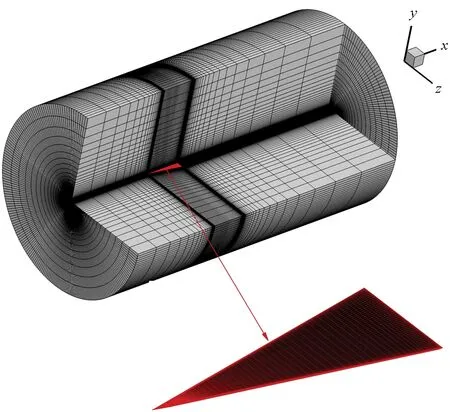
圖3 80°后掠三角翼網格分布Fig.3 Grid distribution of the 80° swept delta wing

1.2 數值方法

采用非定常N-S方程組和滾轉動力學方程描述三角翼單自由度搖滾運動[20]，貼體坐標系(t,ξ,η,ζ)下的方程寫為：

(1)

基于結構網格的有限體積法，采用Roe格式和含雙時間步的LU-SGS方法離散非定常N-S方程組。滾轉動力學方程采用時間二階精度的單邊差分離散，得到時間二階精度的滾轉差分方程：

(2)

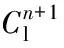
非定常N-S方程組和滾轉動力學方程的耦合求解采用松耦合模式，即由滾轉動力學方程提供三角翼n+1時刻的位置，再由非定常N-S方程組計算n+1時刻的滾轉力矩系數。

遠場采用無反射邊界條件，壁面邊界取絕熱壁，壓力條件為?p/?n|wall=-ρawall·nwall，速度條件為無滑移條件，即V=Vwall。

1.3 驗證與確認

本文的計算基于國防科技大學劉偉教授團隊開發的飛行器動態特性研究程序(Aircraft Dynamic Characteristics Research Program, ADCRP)。該程序針對多塊對接結構網格，求解三維非定常RANS方程，經過二十余年的發展，具備復雜飛行器流動/運動耦合的多自由度非定過程的數值模擬能力。該程序采用系列標模外形進行了系統的驗證與確認計算，適用于三角翼等定、動姿態非定常問題的分析[20-21]，在多個型號項目中得到了應用。該程序具備模擬細長三角翼搖滾現象的研究能力。

2 前緣構型對搖滾特性的影響

考察前緣構型對細長三角翼搖滾特性的影響。計算時，給定來流馬赫數Ma=0.2，基于根弦長度的雷諾數Re=0.4×106，無量綱滾轉轉動慣量Ixx=0.1，滾轉軸與x軸重合且位于上翼面，不計軸承阻尼。統一給定10°的初始滾轉角，研究不同前緣三角翼的滾轉響應，分別對分岔攻角和搖滾振蕩的振幅進行討論。

2.1 前緣形狀對分岔攻角的影響

文獻[22]指出，三角翼攻角α變化會導致其橫向穩定性發生Hopf分岔，存在攻角的臨界值，攻角小于該值，三角翼橫向動態穩定，大于該值，三角翼發生橫向失穩，形成大幅度自維持的極限環振蕩，該臨界值稱為分岔攻角。

對分岔攻角的數值模擬結果如圖4所示，顯示了下削尖、雙面削尖、上削尖三種前緣構型的三角翼不同攻角下的滾轉角時間歷程。按照文獻描述，易于判斷下削尖前緣三角翼分岔攻角約為22.4°，雙面削尖前緣三角翼分岔攻角約為16.9°，上削尖前緣三角翼分岔攻角約為15.5°。其中：下削尖前緣三角翼能夠在較大的攻角范圍保持滾轉穩定性，分岔攻角最大；上削尖前緣三角翼分岔攻角最小，即最容易發生橫向失穩；雙面削尖前緣的三角翼橫向穩定性介于二者之間。

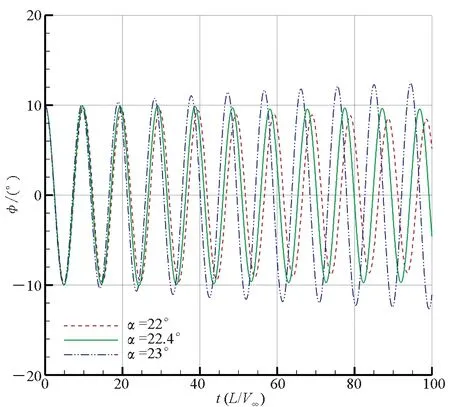
(a) 下削尖前緣(a) Down beveled leading edge

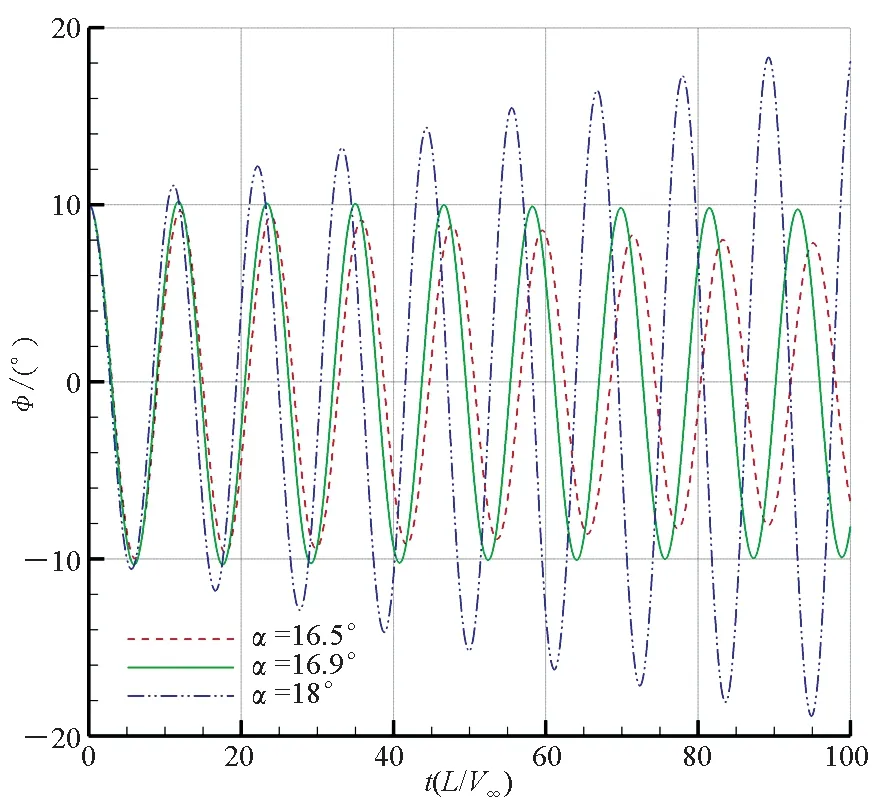
(b) 雙面削尖前緣(b) Double beveled leading edge

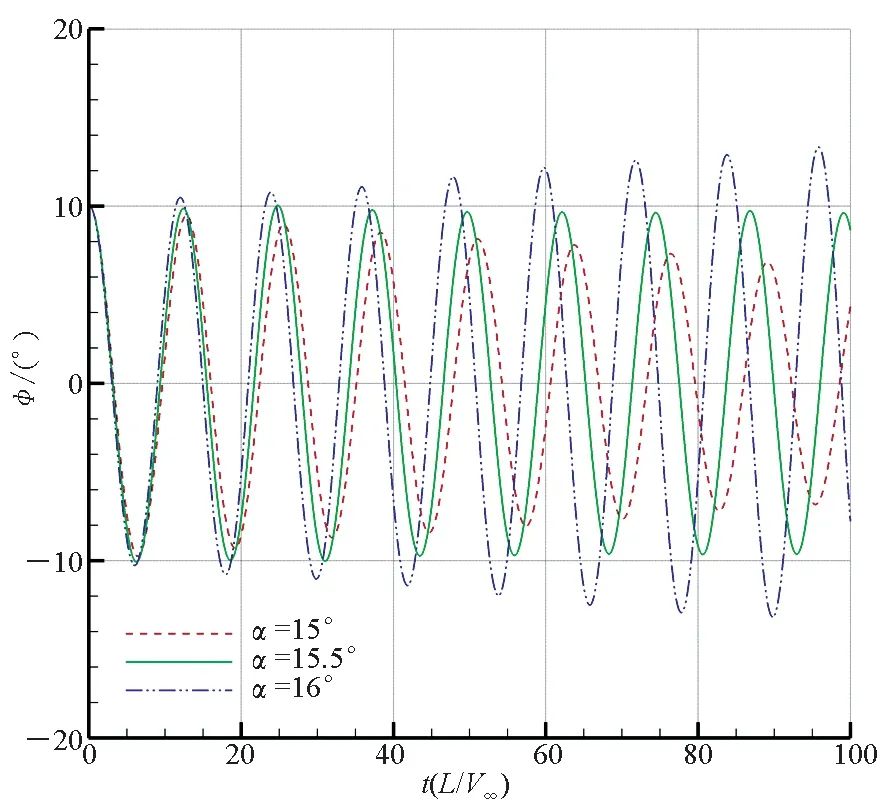
(c) 上削尖前緣(c) Up beveled leading edge圖4 不同前緣形狀三角翼的滾轉角時間歷程Fig.4 Time history of roll angle of delta wing with different leading edge

為進一步理解前緣構型對三角翼動態特性的影響，基于強迫簡諧分析法計算三角翼滾轉穩定性參數，如表1和表2所示。穩定性參數為負則表示具有穩定性，為正則表示不穩定。由表1可知：不同前緣構型的三角翼，在所研究的攻角范圍內都是靜穩定的，整體而言，靜穩定性相當。由表2可知：隨著攻角增大，滾轉阻尼導數由負變正，表明從滾轉動穩定變為滾轉動不穩定，從動態穩定性的角度說明了三角翼滾轉方向發生Hopf分岔的這一現象。其中，下削尖三角翼在22.4°、雙面削尖三角翼在16.9°、上削尖三角翼在15.5°時，滾轉阻尼導數的絕對值顯著小于其他角度的絕對值，這表明此時三角翼幾乎處于無阻尼狀態，正好對應三角翼在跨過該攻角時的滾轉穩定性性態的變化，分岔攻角在以上角度附近。

表1 三角翼滾轉靜穩定性導數

表2 三角翼滾轉阻尼導數

2.2 前緣形狀對振幅特性的影響

上一節的研究表明，攻角大于分岔攻角以后，均會發生橫向失穩，形成大幅度自維持極限環形式的搖滾現象。為進一步考察不同前緣構型的三角翼橫向失穩以后的動態特性，選取25°和30°攻角，給定0°初始滾轉角，研究前緣形狀對三角翼振幅特性的影響，結果如圖5所示。

25°攻角時，如圖5(a)所示，三種前緣構型的三角翼均形成了極限環形式的等幅振蕩，下削尖前緣三角翼的振幅約為19.2°，雙面削尖前緣三角翼的振幅約為65.2°，上削尖前緣三角翼的振幅約為75.6°。其中，下削尖三角翼振幅最小，雙面削尖三角翼次之，上削尖三角翼的振幅最大，對比表2數據，三種前緣構型的三角翼的滾轉阻尼導數均為正，從數值上而言，下削尖三角翼最小，雙面削尖三角翼次之，上削尖三角翼最大，三角翼自激滾轉振蕩的表現與動態穩定性參數預示的規律一致。

30°攻角時，如圖5(b)所示，三種機翼均最終形成了極限環形式的等幅振蕩，但雙面削尖和上削尖前緣的三角翼在發生翻轉后繞滾轉軸進行滾轉振蕩。其中，雙面削尖前緣三角翼搖滾振幅約為49.8°，上削尖前緣三角翼搖滾振幅約為31.4°，下削尖前緣三角翼未發生翻轉，其振幅約為37.1°。

理論上講，雙面削尖前緣三角翼，上下對稱，翻轉后與自身同構，上削尖前緣三角翼與下削尖前緣三角翼在結構上相同，僅與來流在空間的相對位置不同。上削尖前緣三角翼翻轉后，空間位置與下削尖前緣三角翼相同。但由圖5(b)觀察到的結果，上削尖前緣三角翼翻轉后的振幅(31.4°)與下削尖前緣三角翼的振幅(37.1°)并不相同。經分析，主要由于翻轉后滾轉軸位置不相同，對于雙面削尖的三角翼同樣存在該問題，需要進一步分析。

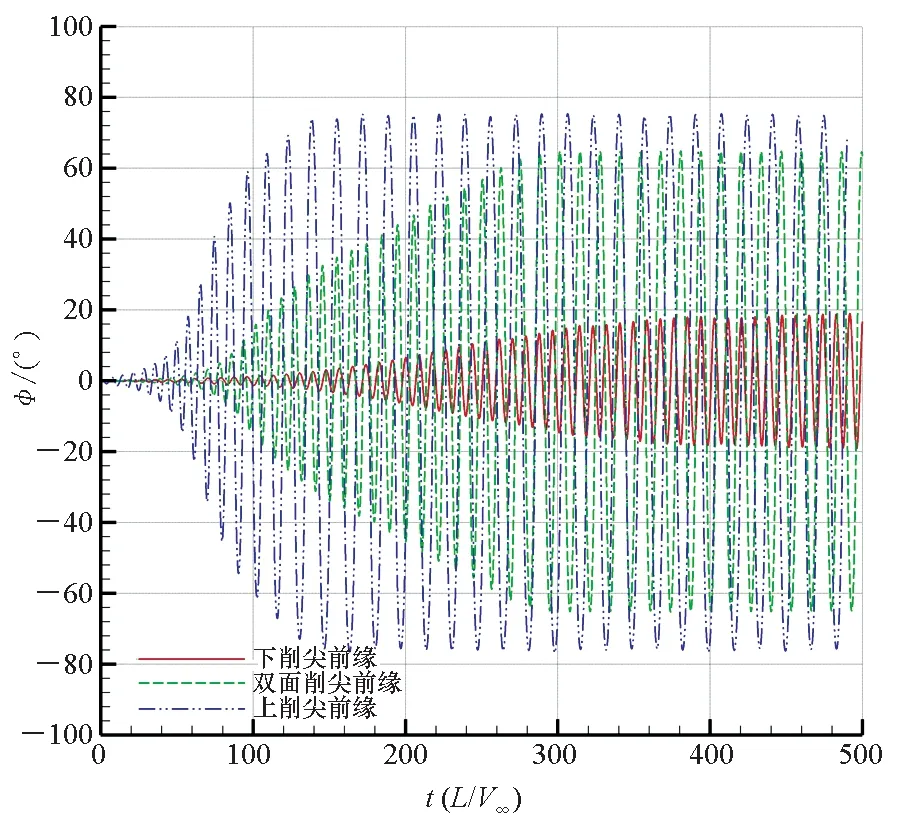
(a) α=25°

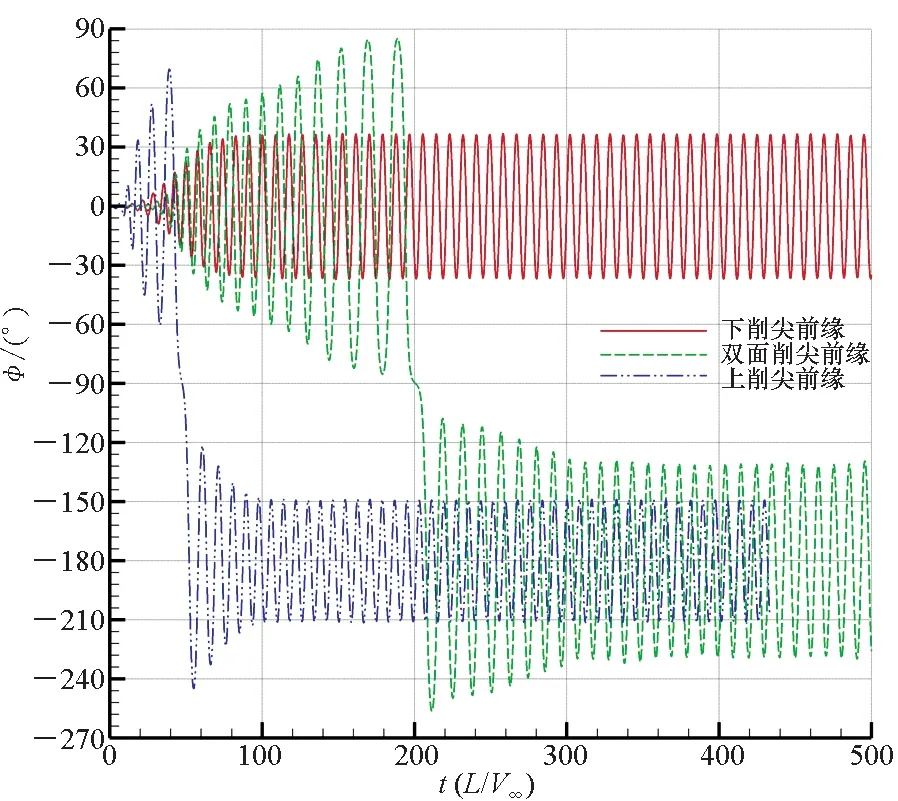
(b) α=30° 圖5 不同前緣構型三角翼在大攻角下的搖滾特性Fig.5 Wing rock characteristics of delta wing with different leading edge in high angle of attack

3 滾轉軸位置對搖滾特性的影響

基于對三角翼搖滾現象的理解，進一步考察滾轉軸位置對細長三角翼搖滾特性的影響。計算時，給定來流馬赫數Ma=0.2，基于根弦長度的雷諾數Re=0.4×106，無量綱滾轉轉動慣量Ixx=0.1，統一指定10°的初始滾轉角，不計軸承阻尼。選取下削尖三角翼，指定不同滾轉軸位置，如圖2所示，研究滾轉軸位置對搖滾特性的影響，分別對分岔攻角和搖滾振幅進行了討論。

3.1 滾轉軸位置對分岔攻角的影響

如圖6(a)所示，滾轉軸位于下翼面下方5 mm處時，三角翼從10°初始滾轉角釋放后，在25°攻角下搖滾振幅呈衰減狀態，在30°攻角下搖滾振幅呈增大狀態，而在27°攻角時搖滾振幅基本保持10°不變，說明滾轉軸位于下翼面下方5 mm的三角翼的分岔攻角約為27°。由圖6(b)～(d)易知，滾轉軸位于下翼面的三角翼分岔攻角為26.5°，滾轉軸位于上翼面的三角翼分岔攻角為22.4°，滾轉軸位于上翼面上方5 mm處的三角翼的分岔攻角為17.4°。由此可見，隨著滾轉軸從下翼面下方5 mm處移動到上翼面上方5 mm處，三角翼的分岔攻角逐漸減小。可以得出結論，在所研究的滾轉軸位置范圍內，滾轉軸位置越高，三角翼搖滾的分岔攻角越小，越易于橫向失穩，反之亦然。

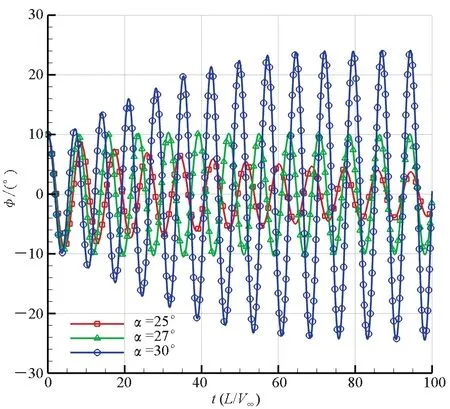
(a) 滾轉軸位于下翼面以下(Axel_DD)(a) Roll-axis under the lower wing surface(Axel_DD)

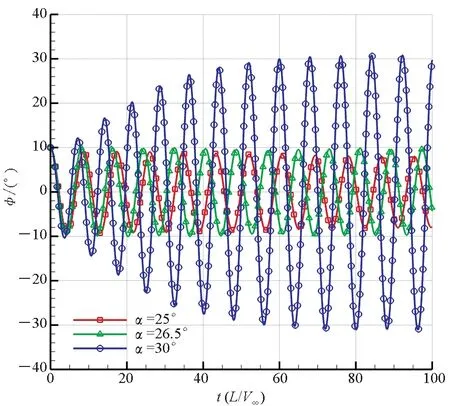
(b) 滾轉軸位于下翼面(Axel_D)(b) Roll-axis on the lower wing surface(Axel_D)

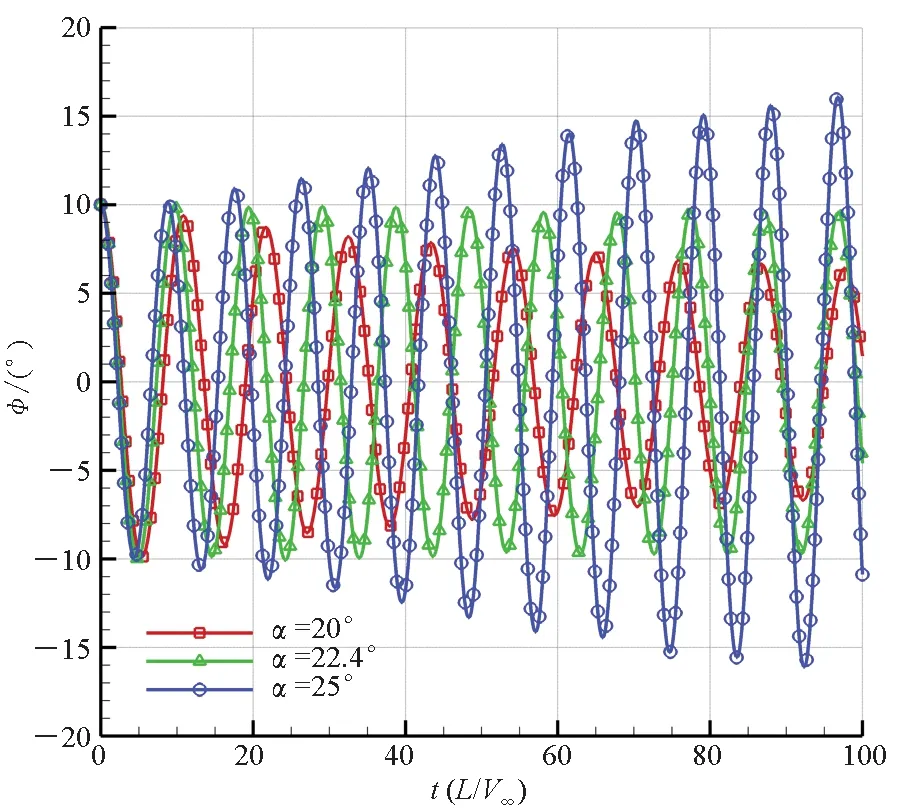
(c) 滾轉軸位于上翼面(Axel_U)(c) Roll-axis on the upper wing surface(Axel_U)

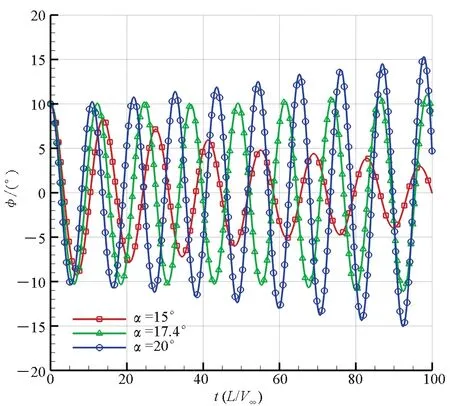
(d) 滾轉軸位于上翼面以上(Axel_UU)(d) Roll-axis above the upper wing surface(Axel_UU)圖6 不同滾轉軸位置的三角翼滾轉角時間歷程曲線Fig.6 Roll angle time historical solution of delta wing installed at different roll-axes

3.2 滾轉軸位置對振幅特性的影響

進一步研究滾轉軸位置對三角翼振幅特性的影響，給定30°、40°、50°和60°攻角，模擬四種滾轉軸位置的三角翼搖滾振幅特性，計算結果如圖7所示。

從圖7中可以看出，四種滾轉軸位置下搖滾振幅隨攻角變化的規律基本一致，30°攻角時，四種滾轉軸位置的三角翼均形成了極限環自激搖滾，滾轉軸位置越靠上振幅越大；40°攻角左右建立最大振幅，隨著攻角進一步增大，由于受到渦破裂的影響，搖滾振幅隨攻角增大而減小；當攻角增加到60°以后，四種滾轉軸位置的三角翼均難以形成大幅度的搖滾振幅。

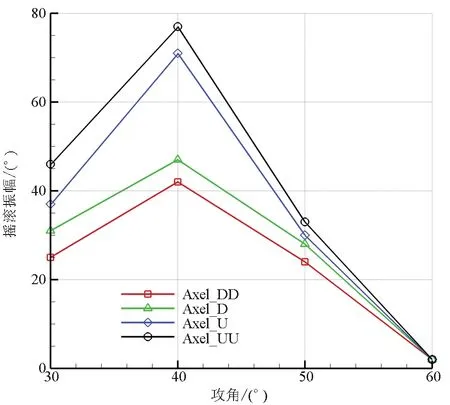
圖7 搖滾振幅隨攻角變化曲線Fig.7 Amplitude of roll varies with attack angle

4 結論

耦合求解三維非定常N-S方程和歐拉剛體動力學方程組，研究了前緣構型與滾轉軸位置對80°后掠平板三角翼搖滾特性的影響，得到以下結論：

1)前緣削尖方式不改變三角翼橫向動態穩定性的性態，但影響三角翼搖滾的分岔攻角和搖滾振幅；不同前緣構型三角翼的自激搖滾特性與動態穩定性參數表征的穩定性一致。

2)對于轉軸位于上表面的三角翼，攻角25°時,前緣下削尖時搖滾振幅最小，上削尖時搖滾振幅最大；攻角30°時，雙面削尖前緣和上削尖前緣的三角翼自激搖滾時發生了翻轉，翻轉后繞滾轉軸等幅振蕩，雙面削尖前緣與上削尖前緣三角翼先翻轉后再形成極限環形式的等幅振蕩。

3)滾轉軸的安裝位置影響三角翼的搖滾特性，滾轉軸位置越高，三角翼搖滾的分岔攻角越小，極限環滾轉振蕩的振幅越大，反之亦然。

三角翼搖滾現象研究多年依然是熱點問題，對其產生和維持機理已有較多深刻的認識，但對敏感因素的分析還不足，旋渦等流動結構與飛行器之間作用的過程和機理等問題仍值得進一步的分析。