基于振動采摘的蘋果樹枝干動力學特性

劉曉雯，郭彩玲

(唐山學院，河北省智能裝備數字化設計及過程仿真重點實驗室，河北 唐山 063000)

蘋果振動采摘的工作原理是借助振動發生器在蘋果樹的樹干、主枝上施加周期性的載荷，通過各級分枝、果柄傳遞給蘋果使其按一定的方式振動，當振動產生的慣性力超過蘋果與果柄的分離力時，蘋果在與果枝或果柄最弱的連接點脫離，從而完成采摘[1-3]。由此可見，蘋果能否在適當的載荷形式與大小的作用下，達到最佳振動狀態，主要取決于蘋果振動時產生的慣性力，而慣性力的主要影響因素是加速度，因此研究加速度響應是蘋果樹動力學研究的重點。

本研究建立了果樹的動力學模型和有限元模型，并采用有限單元法，對蘋果樹進行模態和諧響應分析，確定了蘋果振動采摘時施加給不同直徑范圍的樹枝干的最佳激振頻率。

1 建立果樹模型

本研究采用錨固形式為固定約束方式。由于振動時蘋果樹樹葉產生的黏性阻尼非常復雜[4]，故將系統阻尼等效為Rayleigh阻尼。主要分析無葉蘋果樹枝干的動力學特性。

在河北省遷安市太平鄉尚莊蘋果采摘基地(118.8°E，39.9°N)，隨機選擇自然生長狀態下樹齡約5 a的自由紡錘形宮藤富士蘋果樹3棵，樹高3.4～3.8 m，主干高75～85 cm，株距2.5 m，行距5 m，行間生草，土壤為尚莊蘋果采摘基地的有機土壤，種植期間灌水條件良好，春季修剪。考慮果樹被周圍其他果樹遮擋，影響點云質量，采用Trimble TX8三維激光掃描儀分別對3棵目標果樹在以樹干為圓心，半徑約4 m的區域實施五站式掃描。考慮到點云數據的配準問題，采用標直徑為100 mm靶球作為配準基準[5-7]。2018年5月至2019年5月期間，對3棵目標蘋果樹冠層進行了8次數據采集，掃描實景如圖1所示。

圖1 掃描實景Fig. 1 Real apple vibration picking practice

蘋果樹枝干分支較多，需將蘋果樹枝干結構簡化成三部分: 主干、一級分支枝條和二級分支枝條，如圖2所示。其中，一級分支枝條由主干分生，如圖中Y1，Y2，Y3…Y15；二級分支枝條由一級分枝枝條分生，如圖中由一級分支枝條Y1分生出的Y1a,Y1b,Y1c,Y1d,Y1e,Y1f,Y1g和Y1h枝條。

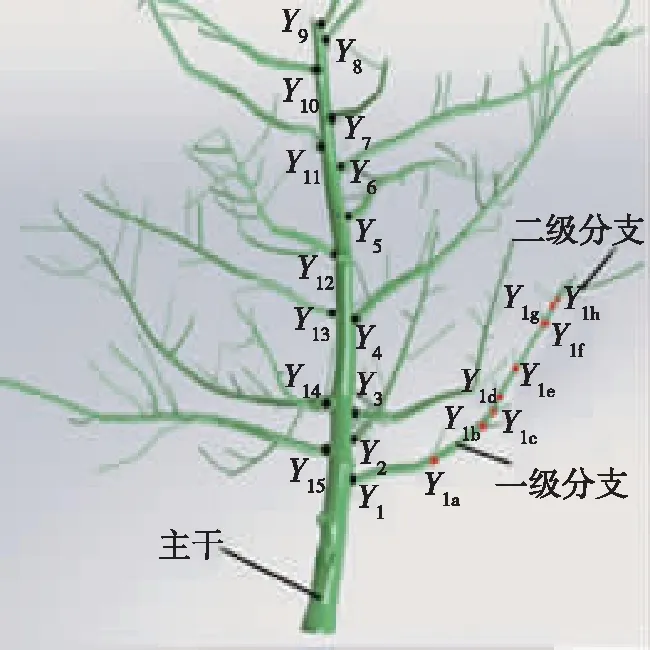
圖2 蘋果樹枝干結構劃分圖Fig. 2 Structure partition map of apple tree branches and trunk

考慮蘋果多生長在二級枝條上，而二級枝條振動時對一級枝條的振動性能影響較小[8-9]，故在掃描所得的蘋果樹模型基礎上除去二級分支及其上蘋果以提高仿真計算的效率。選取3個目標果樹中點云重建后枝干恢復最好的模型進行分析，簡化后的蘋果樹模型如圖3所示。

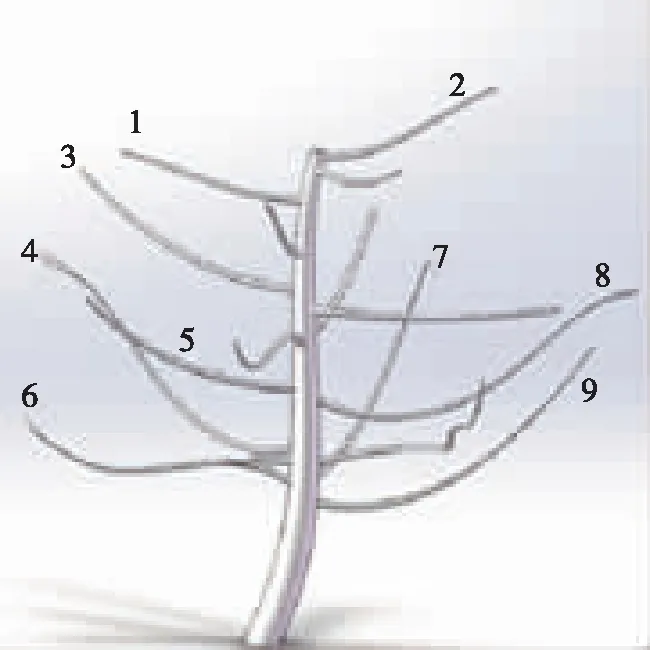
圖3 蘋果樹模型Fig. 3 Modeling of apple tree

1.1 建立基于梁理論的枝干動力學模型

為了分析蘋果樹枝條和蘋果樹整體之間的關系，現建立基于梁理論的枝干動力學模型。

由于蘋果樹為細長狀，故采用歐拉-伯努利梁理論[10]。假設蘋果樹的主干是變截面梁，截面半徑為:

(1)

式中：rz表示蘋果樹主干高度為zmm處的截面半徑，mm；r0為蘋果樹主干位于地面上的底部半徑即rmax，mm；H為蘋果樹主干總高，mm；λ為截面收縮率；β為常數，此處取1。

假設蘋果樹小枝條和大枝條為等截面梁。采用分段等效的方法[11-12]，將蘋果樹主干簡化為變截面懸臂梁，枝條為等截面小梁，樹葉簡化為附加質量和阻尼。蘋果樹主干變截面梁模型和枝條等截面梁模型結構簡圖如圖4所示。

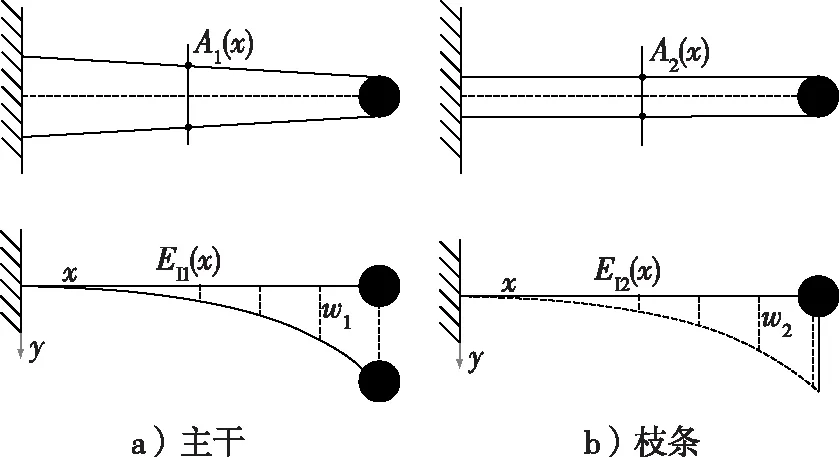
圖4 主干和枝條的結構簡圖Fig. 4 Structural sketch of trunk structure and branches

圖4中，主干和枝條均簡化為左端固定支撐的懸臂梁，且分段截取的長度均為l。固定端為零點，軸線方向的坐標為x。梁的右端分別為一個集中質量為m1的變截面梁和集中質量為m2的等截面梁，梁的橫截面積分別為A1(x)和A2(x)，彎曲剛度分別為EI1(x)和EI2(x)，梁的撓度即垂直于中心軸線的位移分別為w1(x)和w2(x)。

1.2 建立坐標系并定義自由度

定義蘋果樹干位于地面上的底部以及枝條根部為坐標系原點，Y軸為樹干底部以及枝條沿其生長方向的切向。

找到一個Y軸所在的平面Q，Q平面內所有枝干上的點到該平面的距離加權平方和最小[13-14]，即滿足：

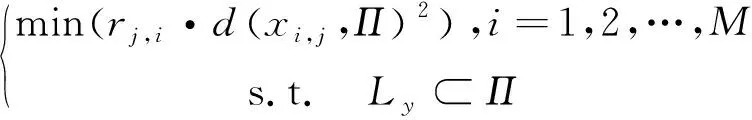
(2)

式中：xi,j表示第i條骨架線上第j個骨架點，其對應的半徑為ri,j；d(xi,j,Π)表示點到面的距離函數；Ly表示Y軸對應的直線；Π為待求的平面。

令平面Π為世界坐標系的XY平面，由此確定X軸，界坐標系的Z軸用右手準則確定。建立蘋果樹梁單元坐標系并定義單元自由度：沿X和Z軸的移動以及X、Y和Z軸的轉動。

2 建立蘋果樹枝干有限元模型

由于基于梁理論的枝干動力學模型簡化太多，故需在其基礎上建立更精確的有限元模型進行動力學分析[15-16]。

2.1 建立有限元模型

建立蘋果樹有限元模型時，作如下的簡化假設：定義蘋果樹主干位于地面上的底部與地面是固定連接；定義主干與枝條的連接處是固定連接且共用一個節點。

將掃描得到的蘋果樹模型導入到有限元分析軟件Ansys Workbench中。

2.2 定義材料屬性

在尚莊采摘基地任取10個蘋果樹枝條樣本進行測量，取平均密度：ρ=0.976×103kg/m3；經基頻實測，得到泊松比μ=0.326～0.349，由于泊松比對頻率影響不大，故取μ=0.33。

由于枝干采用懸臂梁的固定方式，根據歐拉-伯努利梁理論，動態彈性模量[17-19]：

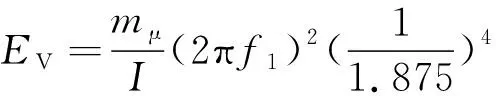
(3)

式中：mμ為單位長度質量，kg/m；f1為第1階共振頻率，Hz；l為懸臂梁長度，m；I為截面的轉動慣量，kg·m2。

計算得彈性模量E=6.38×107Pa。

2.3 選取單元網格劃分

初選8節點的六面體單元SOLID185，但蘋果樹模型因其形狀的復雜性無法劃分出六面體單元，單元出現退化的六面體單元即四面體單元，故選擇10節點的帶中間節點的四面體單元SOLID187，從而保證較高的計算精度。

網格劃分借助Smart Size自由網格劃分工具。

2.4 約 束

采用固定約束方式。

2.5 仿真分析

2.5.1 模態分析

考慮到枝干在高頻振動下易損傷[20-21]，故選取低頻為主要影響頻段，模態分析只取蘋果樹動力學特性中前12 階進行研究，如表1所示。

表1 蘋果樹前12階固有頻率與共振頻率Table 1 The first 12 natural frequencies and resonance frequencies of apple trees Hz

由表1中仿真得到的固有頻率可知：第1階和第2階、第3階和第4階、第5階和第6階、第7階和第8階、第9階和第10階、第11階和第12階固有頻率比較接近。這是由于蘋果樹結構具有一定的對稱性，導致模態成對出現且每對類似，故前12 階中每對相似振型選取一個，即第1，3，5，7，9和11階振型，如圖5所示。

圖5 固有頻率及振型Fig. 5 Natural frequencies and modes

2.5.2 諧相應分析

建立蘋果的受力分析模型，如圖6所示。

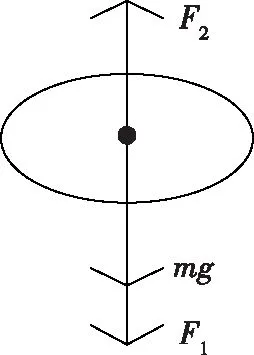
圖6 蘋果受力分析模型Fig. 6 Force analysis model of an apple

由靜力平衡條件：

F1+mg-F2=ma

(4)

式中：F1為作用于蘋果的激振力，N；F2為果柄和蘋果之間的約束力，F2=1.5 N[22]；m為蘋果的平均質量。2019年9月，在圖1所示目標樹上任意摘10個蘋果，稱質量取平均值，m=248 g。a為蘋果脫離果柄后下落的加速度，a=2g[22]，其中g為重力加速度。故：

F1=ma+F2-mg=0.248×9.8×2+1.5-0.248×9.8=3.93 N。

激振載荷：

F=Asin(ωθ+Φ)

(5)

式中：Φ=0；F為激振載荷，N。

由于載荷施加在樹干上，需要較大的激振載荷，效率不高且對蘋果樹會有損傷，故正弦載荷施加在大枝條X方向上距離連接點20 mm處。

如圖3所示，對經掃描并提取點云處理后得到的蘋果樹模型各根主要枝條進行編號。經現場測量，各根枝條的平均直徑如表2所示。

表2 枝條平均直徑 Table 2 Average branch diameters

正弦激振力作用下，各根枝條的位移和加速度響應如圖7所示。

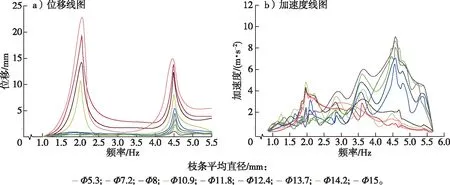
圖7 枝條位移、加速度響應曲線Fig. 7 Harmonic response curves of branch displacement and acceleration

由圖7可得：

1)激振力頻率為2.2 Hz時，枝條位移較大，即擺動幅值較大；激振力頻率為3.5 ～5.1 Hz時加速度較大。由此可見，激振率頻率較高時，更有利于振動動能的傳輸。

2)相同激振力作用下，施加不同的振動頻率，每個分枝的最大位移和加速度不同，該結論與模態仿真分析的結論一致。

3)各直徑枝條最大加速度對應的激振頻率即仿真所得的最佳激振力頻率，如表3所示。

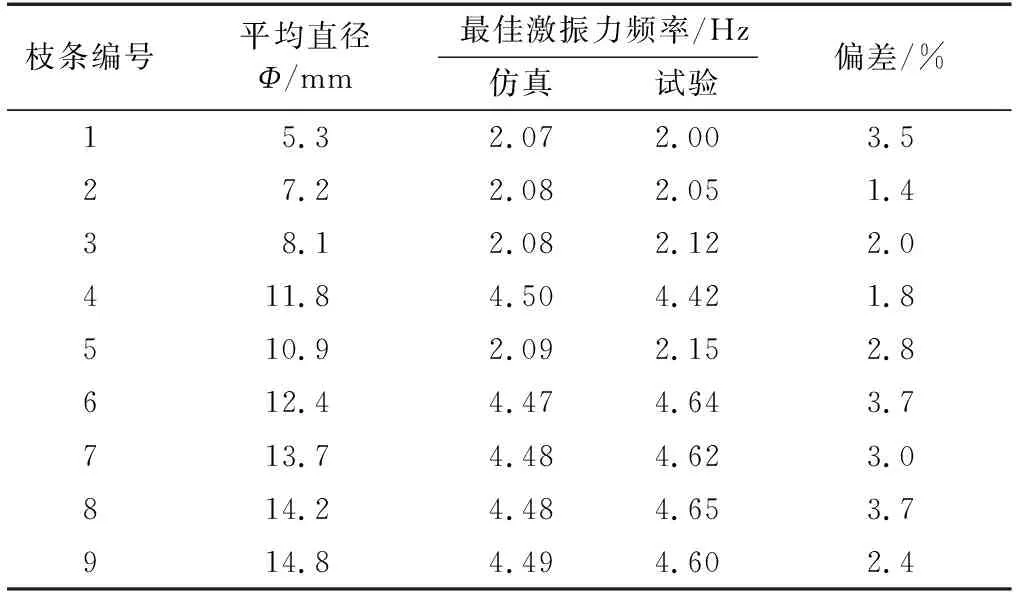
表3 試驗與仿真下枝條激振力頻率對應表Table 3 Corresponding table of excitation force frequency of branches from tests and simulations

由表3中仿真得到的最佳激振力頻率可知，編號為1，2，3，5的枝條, 直徑范圍為Φ5～11 mm，最佳振動頻率為2.08 Hz；表3中編號為4，6，7，8，9的枝條，直徑范圍為Φ12～15 mm，最佳振動頻率為4.48 Hz。

3 共振頻率試驗

2019年10月17日至2019年10月30日，在河北省遷安市太平鄉尚莊蘋果采摘基地，隨機選取10棵樹齡約5 a的自由紡錘形宮藤富士蘋果樹作為試驗對象，蘋果樹高3.5～3.8 m，主干高75～85 cm，蘋果樹平均冠幅0.8～1.3 m，株距2.5 m，行距5 m。實驗儀器：加速度傳感器、AVANT數據采集與信號分析儀、由得偉馬刀具改裝的無級振動發生器，頻率可由PWM 控制器無極調節。實驗內容：每棵目標蘋果樹上隨機選取9條側枝(一級分支)，9條側枝分別與諧響應仿真分析中編號1～9的9條一級分支枝條直徑接近，且側枝上長有蘋果。選取在X方向距離連接點20 mm處設置一個測試點。對每條側枝進行 3 次重復試驗取平均值。最終得到各直徑枝條FFT變換后的加速度響應曲線如圖8所示。為直觀對比試驗得到的共振頻率與仿真得到的固有頻率間的對應關系，將圖8曲線波峰對應的頻率列入表1中。由于仿真和試驗得到的模態頻率在模態階次上難以形成對應，故表1中模態階次含義不同。

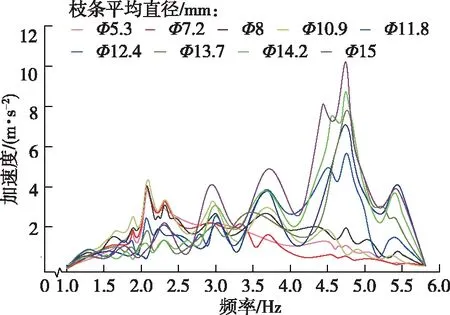
圖8 試驗得到的加速度響應曲線Fig. 8 Acceleration response curves obtained from tests

由表1可知，試驗得出的共振頻率與仿真得出的固有頻率在數值上較接近，第1和2階次、3和4階次、7和8階次、9和10階次、11和12階次固有頻率分別對應1個共振頻率值。分析其原因主要有兩點：

1)重建的蘋果樹模型中枝干恢復不完整，因此固有頻率和共振頻率接近但不相等。

2)相鄰階次固有頻率數值相差較小時，試驗中共振頻率互相干擾，使其中一個共振頻率丟失。

將圖8中各直徑枝條最大加速度對應的激振頻率列入表3最佳激振力頻率(試驗值)中，并與仿真結果對比可知：通過試驗所得的不同直徑枝條的最佳激振力頻率與仿真結果相對應，且數值很接近，最大偏差3.7%。試驗驗證了仿真模型中除去二級枝條及其上蘋果的簡化處理的合理性，以及應用文中所述的仿真方法得到的最佳振動頻率的準確性。

選取表3中枝條激振力頻率偏差較大的枝條，編號為1，6，8和9，分別對比其通過試驗和仿真得到的加速度響應曲線，如圖9所示。

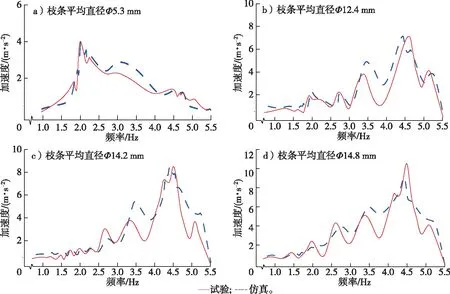
圖9 仿真與試驗下加速度響應曲線對比Fig. 9 Comparisons of acceleration response curves between simulations and tests

經比較發現，雖然仿真與試驗中得到的最佳激振力頻率很相近，但加速度響應曲線存在一定差異，分析差異來源，主要有以下4點：

1)掃描重建的模型由于受光照、風力等干擾因素存在一定的誤差；

2)模型阻尼等效為Rayleigh阻尼，與枝條真實振動時的阻尼具有一定偏差；

3)建立蘋果樹有限元模型時進行了近似性的假設；

4)蘋果樹枝條上分支結點的存在，影響枝條的材料特性。

4 結 論

利用有限元方法，對蘋果樹枝干進行了建模及仿真分析。研究表明，在激振力作用下，枝條的振動具有一定的不相關性，且隨著激振率頻率的增加，振動動能的傳輸更有效。通過模態分析，得到蘋果樹前12階的固有頻率為1.92～5.35 Hz；諧響應分析中，把枝條歸納成Φ5～11 mm和Φ12～15 mm兩種直徑范圍，并得到了兩種直徑范圍枝條的最佳激振力頻率分別為2.08 和4.48 Hz。經現場試驗，驗證了仿真結果的合理性。研究結果為蘋果的振動采摘和采摘設備的研發提供了理論基礎，具有一定的指導意義。