基于SOLO分類理論的高職高考數學試題研究

蘇美婷 陳偉琪

一、引言

隨著我國社會經濟的發展，職業教育備受重視。2019年的《國家職業教育改革實施方案》更提出了“沒有職業教育現代化就沒有教育現代化”的重要論斷。2020年，廣東省“3+證書考試”共錄取56萬多人，比上一年增加12萬人。由此可見，中等職業學校的畢業生除了面向社會選擇就業外，越來越多的畢業生選擇到高等學校繼續進修。數學是“3+證書考試”的必考科目，學生不僅要學習專業課，還要抽出時間復習數學，因此，分析廣東省普通高等學校招收中等職業學校畢業生考試（以下簡稱“高職高考”）的數學試題的考查層次分布情況，可為師生開展科學備考提供參考。

SOLO（Structure of the Observed Learning Outcome）分類評價理論，意為“可觀察的學生學習成果的結構”，是Biggs等人提出的一種以等級描述為基本特征的質性評價方法。SOLO分類評價理論將學生的可見學習成果從低到高分為五種水平：前結構水平、單點結構水平、多點結構水平、關聯結構水平和抽象拓展結構水平。SOLO分類理論為高職高考數學試題的分析提供了很好的工具。

一方面，在滿分150分的試卷中每年幾乎都有近50分的試題牽涉解析幾何的內容，另一方面，教師普遍反映解析幾何難教，學生普遍反映解析幾何難學，因此，有必要對解析幾何試題進行分析。本文將以SOLO分類評價理論作為分析工具，對2016-2020年廣東省高職高考數學試卷中解析幾何部分的試題進行分析，以期為一線中職數學教師的備考提供參考。

二、研究方法

（一）研究對象

本研究選取2016-2020年高職高考數學試卷中涉及解析幾何內容的試題為研究對象，其中選擇題12道，填空題6道和解答題9道。

（二）研究步驟

1.編制試題知識細目表

本文依據廣東省高職高考考試大綱將解析幾何部分的知識點進行細分，編制試題知識細目表，由于數學試題通常涵蓋不同板塊的知識點，為了可以更準確地判斷試題考查層次，也將屬于解析幾何以外的內容納入統計，例如不等式、解三角形等。

2.確定試題的SOLO層次

按照SOLO分類評價理論的基本假設和思路，分析中職學生解答數學試題所必須經歷的思維操作階段，從而確定數學試題的層次水平和能力結構。

SOLO評價理論中的“前結構水平”是指一種低于目標方式的反應，由于高職高考的試題至少涉及一個知識點，所以沒有與“前結構水平”所對應的試題。同時，SOLO評價理論中的“抽象擴展水平”是指學生超越問題情境，得到更抽象、更一般的結論，超出了高職高考數學試題的考查要求。因此，本研究只選取中間三個水平進行分析。下面通過一些具體的實例來說明，運用SOLO分類理論對中職數學試題中的解析幾何部分試題進行分類的具體操作方法。

【案例1】單點結構水平。

（2020年第9題）拋物線y2=4x的準線方程為（? ）

A.y=-1???? B.x=1

C.x=-1D.y=1

分析：“單點結構水平”是指學生只需要找到一個線索并用該線索去解決的問題。此題考查的是拋物線的性質，學生只需識別拋物線的準線方程這一條線索便可解決問題，因此該題是單點結構水平的試題。

【案例2】多點結構水平。

（2018年第13題）已知點A（-1，4），B（5，2），則AB的垂直平分線方程是（? ）

A.3x-y-3=0B.3x+y-9=0

C.3x-y-10=0D.3x+y-8=0

分析：“多點結構水平”是指學生需要兩個或更多的線索，但不需要將它們進行整合就能解決的問題。本題要求學生根據條件求直線方程，涉及中點公式、斜率公式以及直線方程三個知識點，因此，該題是多點結構水平的試題。

【案例3】關聯結構水平。

（2018年第24題）已知橢圓C的焦點F1（-6，0），F2（6，0），C與x軸有一個交點A（-3，0）.

（1）求橢圓C的標準方程;

（2）若P為橢圓C上任意一點，求cos∠F1PF2的最小值.

分析：“關聯結構水平”是指學生需要找到解決問題所需的線索或資料，并將它們進行整合才能得出正確答案的題目，這些線索或者資料通常是涉及兩個或以上的知識板塊。本題涉及橢圓標準方程中a、b、c三個量的理解、橢圓的定義、余弦定理以及求最值等多個知識點，而且需要將這些知識點進行整合才能正確求解，因此該題是關聯結構水平的試題。

三、結果與分析

（一）近5年解析幾何試題知識考查情況

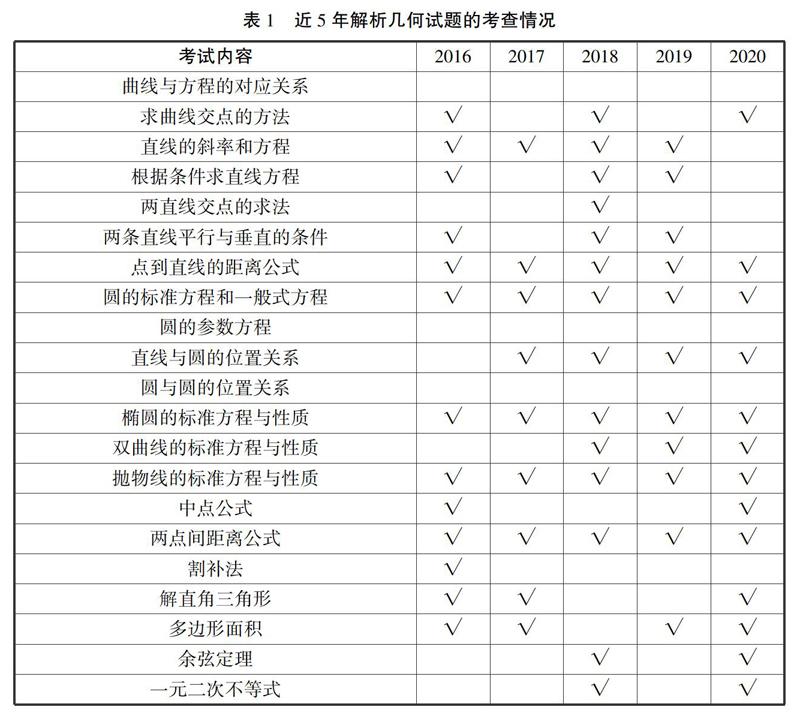
表1列出了近5年高職高考數學試卷中的解析幾何知識考查的情況。試題以能力立意，除了考查解析幾何的主體知識外，還注重以解析幾何為主要載體考查三角、不等式等知識。

近5年的解析幾何試題幾乎涵蓋了考綱要求的所有知識點。“曲線和方程的對應關系”雖然沒有直接的考題，但這是解析法的基礎，換言之，所有題目幾乎都需要根據曲線和方程的關系來理解和解答。除此之外，只有圓的參數方程和圓與圓的位置關系兩個知識點沒有考查到。

個別重點內容是每年都有考查，特別是解析幾何的經典內容，如點到直線的距離、圓和圓錐曲線的方程與性質等。解析幾何是用解析法研究幾何問題，不僅能用于研究三角形、平行四邊形等直線圍成的圖形，更能為二次曲線的研究提供簡便的方法。距離問題是幾何研究中一個重要方向，因此兩點間的距離公式和點到直線的距離公式每年都會考到就不足為奇了。從阿波羅尼發現“圓錐曲線”后，人們對圓錐曲線的認識只有一些零散的增長，直到笛卡爾和費馬創立“解析幾何”，才開啟了用代數方法研究幾何問題的新時代，從此圓錐曲線的發展迎來了春天。所以，盡管圓錐曲線對中職學生而言具有一定的學習難度，但依然受命題者青睞是理所當然的。

（二）SOLO知識點分布情況

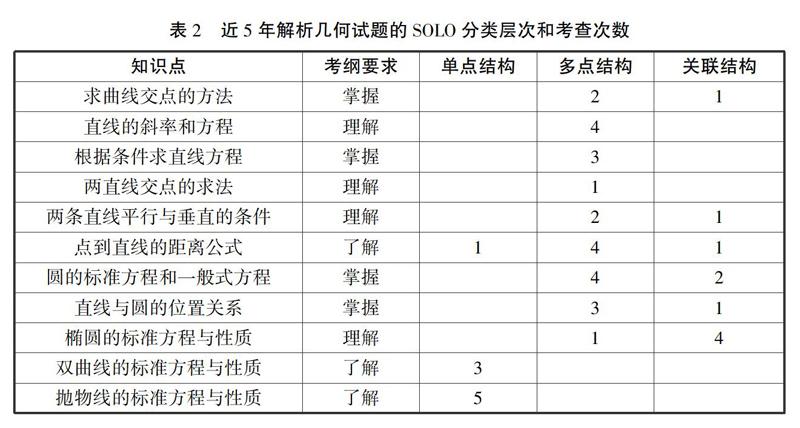
表2列出了近5年解析幾何試題的SOLO分類層次和考查次數，其中知識點只列出考試大綱中解析幾何部分要求的知識點，大綱要求分為了解、理解和掌握三個層次。

從表2我們可以發現，對于了解層次的雙曲線和拋物線的標準方程與性質的試題都是單點結構，對于理解層次的試題則大多以多點結構的形式出現，而掌握層次的試題則多以關聯結構的形式出現，因此，試題的層次清晰，其SOLO層次與考試大綱的要求基本相符。

如前所述，因為距離公式的重要性和應用的廣泛性，所以盡管考試大綱對“點到直線的距離公式”僅作了解要求，但在實際考查中難免會超出這個要求。考綱對“直線的平行與垂直的條件”和“橢圓的標準方程和性質”的要求是理解，但在實際考查中涉及關聯結構，這主要是因為考綱對知識點的認知要求是基于布魯姆的認知分類理論與SOLO分類評價理論的分類標準的差異造成的。所以，SOLO分類評價理論是試題研究的有力補充。

（三）結論

首先，試題全面，基本覆蓋了考試大綱涉及的考試內容，并且對點到直線的距離公式、圓和圓錐曲線的方程與性質等主干知識進行重點考查。

其次，題目的難度設計與考試大綱的認知要求基本相符，強調對數學基礎知識和基本能力的考查，試題的設計有明顯的層次梯度。

四、建議

根據對近5年解析幾何試題的SOLO分類層次，我們提出高職高考數學備考的“點線面體復習體系”。

（一）以知識過關為點

從試題考查的基礎性和全面性可以看出，高職高考數學強調基礎知識。因此，在解析幾何部分的教學及復習中，教師應注重基礎知識的教學，讓學生全面學習并掌握解析幾何的知識和方法，重視概念和公式的準確記憶。其次，教師在教學中應重視知識結構，引導學生理解數學知識的本質，幫助學生建立完整的解析幾何知識體系。

（二）以能力培養為線

基礎知識、基本運算和基本技能，一向是數學教學的重點，高職高考命題素來遵從基礎性原則，傾向于對三基的考查。因此，在教學和復習中，教師應重視數學運算訓練和技能的培養，要求學生一算到底，無論是簡單的移項還是復雜的含參高次運算。教師板演時也要做好示范，不要隨便從略。同時，教師也可以利用 “模仿+變式” 開展題組訓練，來幫助學生掌握公式，提升數學能力。例如在講授點到直線的距離公式時，教師可以通過設計如下問題進行變式訓練。

【案例4】“點到直線的距離”訓練題組。

（1）點P（1，2）到直線l：3x-4y-1=0的距離是______;

（2）原點到直線y=2x+5的距離為______;

（3）點P（1，-2）到直線l：x=4的距離是______;

（4）點P（1，a）到直線l：x-y+1=0的距離是2，則a=______;

（5）原點到直線l：ax-y+8=0的距離是4，則a=______;

（6）已知ΔABC的頂點A（1，1），B（4，2），C（-4，6），則ΔABC的面積為______.

（三）以素養提升為面

學科素養通過基礎教育的學科教學培養形成，既是基礎教育培養的目標要求，也是高校人才選拔的要求。因此，教師在數學教學與復習中要注重提升學生的數學核心素養。數學核心素養主要包括數學運算、直觀想象、邏輯推理、數學抽象、數據分析和數學建模。在講解解析幾何相關習題時，幫助學生讀懂題意來發展他們的數學抽象素養，通過題意想到數學模型來培養他們數學建模的素養，根據題意作出圖形發展他們的直觀想象核心素養，引導學生理清解題步驟來提升他們的邏輯推理能力，在解題的過程中注意培養他們的數學運算能力。

（四）以立德樹人為體

習近平總書記指出教育應全面貫徹黨的教育方針，落實立德樹人的根本任務，數學課程是落實“立德樹人”的一個重要載體，教師可以通過教學內容和教學方法來落實立德樹人。在教學內容方面，從數學文化、數學美、數學史和數學現實出發，用數學本身的特點和價值去體現立德樹人的內涵，將數學自身特點和立德相結合，從而達到育人的目的。在教學方式方面，不僅可以通過講授的形式，還可以通過實物展示或現代教學手段展示實驗過程等教學方式來落實“立德樹人”。總而言之，教師在教學中應以生為本，認清使命，服務發展，腳踏實地上好每一堂課。

[本文是廣東省教育技術中心2018年專項課題“信息技術與中職數學教學深度融合的案例研究”（課題立項號：18JX07334）的階段性成果。]

責任編輯 陳春陽