考慮脈動風場的3 MW 風機鋼塔筒基礎底板脫開失效概率

蔣友寶，劉 志，賀廣零，彭穗湘，鄭峻林

(1. 長沙理工大學土木工程學院，湖南，長沙 410004；2. 華電重工股份有限公司，北京 100070)

開發(fā)風能是解決能源短缺和環(huán)境污染兩大基本問題的有效措施之一。因此，風能技術在國內(nèi)外得到大力發(fā)展。中國從2005 年基本沒有風電發(fā)展到2017 年累計裝機量已經(jīng)占世界總量的35%[1-2]。風機作為高聳結構，其基礎結構的變形特征、力學條件及塔筒的二階效應決定了它自身的整體穩(wěn)定性。大量的風機倒塌事故表明[3]：如果基礎失穩(wěn)，必定會引起風機倒塌等災難性的后果；而導致災害的直接原因主要有地基承載力失效、地基不均勻沉降等惡劣的地質(zhì)環(huán)境，以及雷暴、冰凍、強風、暴雨等不良的氣候條件。例如在強風荷載作用下，風機塔筒時常發(fā)生折斷、基礎底板脫開等，對風機的安全生產(chǎn)構成重大威脅，該現(xiàn)象已引發(fā)了國內(nèi)外許多科學研究工作者的關注[4-6]。

與一般建筑結構不同，風機所承受的荷載中葉輪氣動力一般起控制作用，且該氣動力受風速影響較大。因此，對各種風速工況下風機塔筒及風機基礎進行力學分析，明確其受力情況是保證風機結構安全的前提條件。對風場作用下風機受力的研究，需考慮脈動風的影響。一般可通過現(xiàn)場實測或者風場模擬[7]等手段獲得脈動風時程，再將之用于風機動力響應研究[8-9]。同時，為考慮不確定性因素的影響，風機可靠度的研究也受到較多關注[10-11]。賀廣零等[12-13]基于廣義概率密度演化理論提出了風機抗風動力可靠度分析方法；通過模擬隨機脈動風場，建立了“槳葉-機艙-塔體-基礎”一體化有限元模型，分析了風力發(fā)電鋼塔和鋼筋混凝土風力發(fā)電高塔的抗風動力可靠度。

目前，對風機基礎底板脫開失效概率的研究較少，而實際工程中，因基礎底板脫開導致風機破壞的安全事故時有發(fā)生。鑒于此，本文結合某3 WM 風力發(fā)電高塔系統(tǒng)，分析此類結構在不同風速工況下的基礎底板脫開失效概率，并計算其不脫開失效的可靠度，為風機基礎設計提供參考。

1 風機塔筒結構模型與荷載計算

1.1 塔筒結構模型

某陸上風電場位于非抗震區(qū)，選用3 MW 風機，其葉輪半徑為53 m，共有3 個葉輪，尺寸為53 m×2.8 m×3.6 m(長×寬×高)，塔筒總高度為87.423 m，分為上、中、下三段。塔筒上、中、下段高分別為30 m、30 m、27.423 m，分別由14 個、13 個、12 個變截面塔節(jié)組成[14]。塔筒頂部筒體直徑為3.524 m，塔筒底部筒體直徑為4.181 m，中間塔筒半徑、高度和壁厚都隨高度而變化。風機塔筒簡圖見圖1，具體尺寸見表1。

圖 1 風機塔筒簡圖Fig. 1 Diagram of wind tower tube

1.2 塔筒結構荷載

大型風機塔筒的頂部安裝有風機葉輪，在風場作用下葉輪轉(zhuǎn)動產(chǎn)生較大的氣動力，且葉輪等裝置的重力相對下部塔筒形心有偏心，會產(chǎn)生偏心力矩。相關研究[15-16]表明：塔頂偏心力矩荷載的數(shù)值遠小于塔頂氣動荷載對塔筒底部所造成的彎矩。因此，研究塔筒底部受力時，可對風機塔筒荷載進行簡化，即忽略塔頂偏心力矩的影響，將塔筒所受荷載簡化為風輪及機艙重力Fy、氣動荷載Fx及沿塔筒高度作用的風荷載ωz。其中對于風荷載，主要按順風向荷載效應考慮。塔筒具體受力見圖2。

表 1 鋼塔筒分段尺寸Table 1 Size of steel tower

圖 2 塔筒承受荷載簡圖Fig. 2 Loads of wind tower

對于塔身風荷載，《高聳結構設計規(guī)范》(GB 50135-2006)[17]規(guī)定垂直于風機塔筒表面上的風荷載標準值按式(1)計算：

對于塔筒風機葉輪氣動荷載，按兩種情形：正常運行工況和極端荷載工況予以考慮。

在正常運行工況下，根據(jù)動量-葉素理論葉輪氣動推力可計算為：

對于塔頂重力荷載，可按下式計算：

式中：m1為葉輪質(zhì)量；m2為機艙質(zhì)量；g為重力加速度。

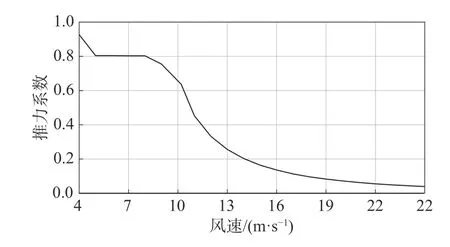
圖 3 不同風速下葉輪推力系數(shù)Fig. 3 Thrust coefficient of impeller with different wind speeds

根據(jù)3 MW 風機廠家的風機總體技術手冊可知：葉輪和機艙的質(zhì)量分別為66.7×103kg 和127.7×103kg。風機塔筒的塔頂氣動力按式(6)、式(7)計算，風機塔筒的塔頂豎向荷載按式(8)計算。

1.3 脈動風場數(shù)值模擬方法

為了較為精確模擬整個塔筒受脈動風速的影響，將塔筒等效為一個39 點的高聳結構模型，各質(zhì)點均位于該節(jié)塔筒的中心點，見圖4。

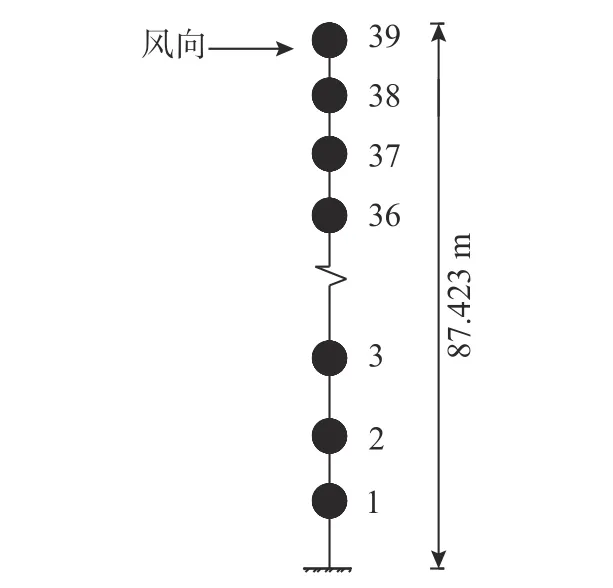
圖 4 風機塔筒結構模型Fig. 4 Wind tower structure model

利用諧波合成法理論及脈動風場模擬方法[7]。所模擬的脈動風速可表達為：

表 2 風速模擬的主要參數(shù)Table 2 Main parameters of wind speed simulation

在風工程領域，應用廣泛的風速譜有Davenport譜、Kaimal 譜[19]等。其中Davenport 譜的表達式為：

根據(jù)本節(jié)介紹的風場數(shù)值模擬方法和基本參數(shù)，利用MATLAB 程序語言編寫模擬單點水平脈動風速時程的程序，進行風場模擬。為了校核整個塔筒模擬所得到的脈動風速是否精確，本文在塔筒的下段取點1、5、10，中段取點15、20、25，上段取點30、35、39，并且將這些點的脈動風速時程功率譜與目標譜(Davenport 譜和Kaimal譜)進行對比分析。可知，兩種工況下大部分點的脈動風速模擬效果比較好，少數(shù)點雖然偏差稍大，但均在工程容許范圍內(nèi)。限于篇幅，僅給出點5 的風速功率譜與脈動風速對比以及選用Davenport譜和Kaimal 譜的總風速對比情況，見圖5。

2 風機塔筒結構動力時程分析

2.1 風機塔筒結構有限元模型

圖 5 點5 風速功率譜與總風速對比Fig. 5 Comparisons between power spectrums of wind speed and total wind speed for point 5

彭文春等[15]、袁萬等[20]采用ABAQUS 軟件對風機鋼塔筒進行了建模，結果表明分析效果較好。參考該思路，采用ABAQUS 軟件按圖1 和表1 建立風機鋼塔筒模型。假定風機鋼材材料為Q345E，密度為7850 kg/m3，彈性模量為2.1×1011Pa，泊松比為0.3。為簡化分析，本文參考文獻[21]假定底面考慮為固定約束，各塔筒段之間采用綁定(tie)約束。

2.2 塔筒的模態(tài)分析

先對該風機塔筒結構進行模態(tài)分析。Tempel等[22]將塔筒頂部的機艙和葉輪等效為一個質(zhì)點，并賦予質(zhì)量，且將此質(zhì)點與塔筒頂部圓環(huán)截面進行耦合。參考該思路，選用ABAQUS 中Lanczos算法進行模態(tài)分析，分析結果見表3。

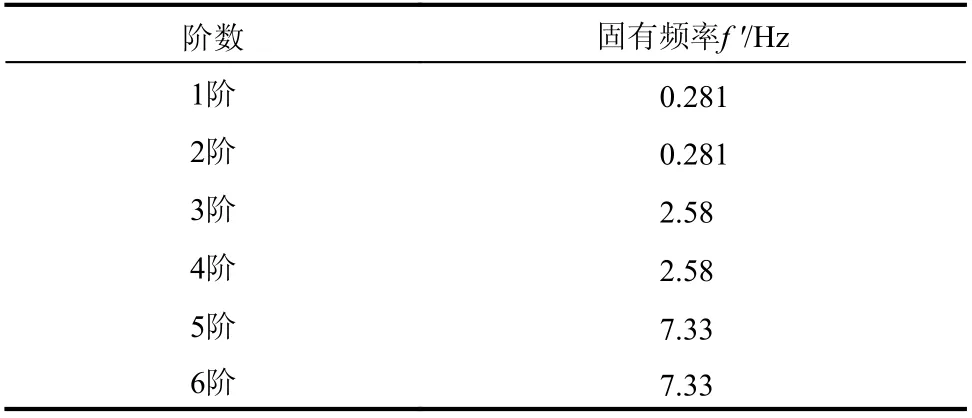
表 3 塔筒前六階固有頻率Table 3 First six natural frequencies of tower

根據(jù)塔筒的第1 階、第2 階固有頻率，按Rayleigh阻尼考慮，對應的阻尼系數(shù) α、λ分別為：

式中：ω1、ω2分別為第1 振型、第2 振型的圓頻率，ω=2πf′，f′為塔筒的固有頻率； ξ為振型阻尼比，根據(jù)《高聳結構設計規(guī)范》(GB 50135-2006)[17]鋼結構阻尼比取0.01。

從表3 可知，風機塔筒的第1 階、第3 階、第5 階的固有頻率分別與第2 階、第4 階、第6 階相同，這是因為風機塔筒在x與z方向?qū)ΨQ，即風機塔筒在這兩個方向的剛度和質(zhì)量相同，這與趙志等[23]的研究結果相吻合。風機塔筒的第1 階固有頻率為0.281 與廠家所提供的數(shù)據(jù)0.283相差僅0.71%，表明本文將葉輪與機艙的質(zhì)量考慮為風機塔筒本身質(zhì)量與原模型基本等效。根據(jù)式(11)、式(12)得出 α、λ分別為0.0176 和0.005 67。

2.3 塔筒的動力時程分析

由式(2)～式(7)，可分別計算出塔筒風荷載和葉輪氣動推力荷載；再考慮塔筒、葉輪和機艙的自身重力，便可得到塔筒的總荷載。將這些荷載分別輸入到ABAQUS 有限元模型中，其中塔頂葉輪和機艙的重力荷載按模態(tài)分析時以點質(zhì)量的形式預先施加，與實際情形相符；而風荷載和葉輪氣動推力時程總長度為200 s，時間間隔為0.2 s，采用隱式分析法進行計算。為使計算結果更為精確，動力時程分析中考慮重力二階效應的影響。對于該塔筒結構，選用Davenport 譜、Kaimal 譜模擬脈動風速得到的荷載效應均有較大波動。限于篇幅，僅列出選用Davenport 譜模擬脈動風速時正常運行工況與極端荷載工況下塔筒底部的彎矩時程曲線以及產(chǎn)生最大應力時間點的應力云圖，見圖6。

圖 6 選用Davenport 譜時兩種工況下動力時程分析結果Fig. 6 Results of dynamic time history analysis under two working conditions using Davenport spectrum

可見，當采用Davenport 譜時，在正常運行工況下：塔筒底部最大的彎矩為5.85×107N·m，最大應力為135 MPa；在極端荷載工況下：塔筒底部最大的彎矩為1.10×108N·m，最大應力為286 MPa。由于鋼材屈服強度為345 MPa，兩種工況下最大應力值均小于鋼材的屈服強度，滿足強度要求。

3 風機塔筒基礎脫開失效概率

3.1 風機塔筒結構荷載效應統(tǒng)計模型

如前所述，由于風機塔筒所受風荷載和葉輪氣動推力都會隨時間的變化而變化，因而塔筒底部的剪力和彎矩等作用效應波動變化顯著。記Sk為作用效應的標準值，分別按規(guī)范[17]設計方法和式(6)、式(7)計算確定風荷載和葉輪氣動力的標準值，并利用有限元靜力分析得出兩種工況下塔筒底部彎矩M、剪力V、軸力N的標準值，計算結果見表4。

表 4 作用效應標準值Table 4 Standard value of action effect

記μ為其對應的作用效應均值。定義一系數(shù)κ，其計算式為：

先對兩種工況下分別按式(6)和式(7)計算的塔筒頂部氣動推力進行統(tǒng)計分析，所得結果見表5。可見，無論是選用Davenport 譜還是Kaimal 譜，正常運行工況下葉輪氣動推力的變異性均較極端荷載工況要小一些。而相同運行工況下，按Davenport譜考慮時葉輪氣動推力的變異性要大一些。

表 5 風荷載時程下塔頂氣動推力的統(tǒng)計參數(shù)Table 5 Statistical parameters of aerodynamic thrust on tower top under wind load time history

根據(jù)第2.2 節(jié)的動力時程分析，可對各作用效應的結果進行統(tǒng)計分析。例如對于塔筒底部彎矩和剪力，其頻數(shù)直方見圖7。

圖 7 彎矩和剪力頻數(shù)直方圖Fig. 7 Frequency histogram of bending moment and shear

對彎矩、剪力時程分析結果進行相關性分析表明：采用Davenport 譜時，正常運行和極端荷載工況下的彎矩、剪力的相關系數(shù)分別為0.981 和0.873；采用Kaimal 譜時，正常運行和極端荷載工況下的彎矩、剪力的相關系數(shù)分別為0.955 和0.805。為簡化考慮，假定兩者完全相關。若用極值I 型分布來擬合，部分擬合效果對比見圖8。可知，在圖8(a)中，全段曲線擬合效果較好；在圖8(b)中，當累積分布概率大于0.5 時，曲線擬合效果較好；在圖8(c)中，當累積分布概率大于0.3 時，曲線擬合效果較好；在圖8(d)中，當累積分布概率大于0.4 時，曲線擬合效果較好。需說明的是，上述區(qū)域正是對失效概率有重要貢獻的區(qū)域，雖然其他區(qū)域的擬合效果較差，但對失效概率的影響較小，即對可靠度的計算結果影響不大。因此，本文假定正常運行工況與極端荷載工況下塔筒底部的彎矩和剪力均為極值I 型分布，且完全相關，相應的統(tǒng)計參數(shù)見表6。

圖 8 彎矩和剪力的極值I 型擬合曲線Fig. 8 Extreme value I-type fitting curve of bending moment and shear force

由表6 可知，塔底彎矩、剪力的變異系數(shù)較表5 中風機氣動力變異系數(shù)高出較多。原因主要是塔筒受自身高度范圍內(nèi)的脈動風場影響較大，且重力二階效應顯著，使得總效應的變異系數(shù)較風機氣動力有較大增加。

3.2 標準模型基礎底板脫開失效概率

風機基礎主要承受上部結構傳來的作用以及自身和覆土自重，見圖9，其中M、F為風機上部結構傳遞過來的彎矩、水平力；N為風機上部結構傳遞過來的軸力；N1為基礎混凝土自重；N2為基礎以上覆土自重；R為基礎底板半徑；h為上部荷載作用點到基礎底部的距離。

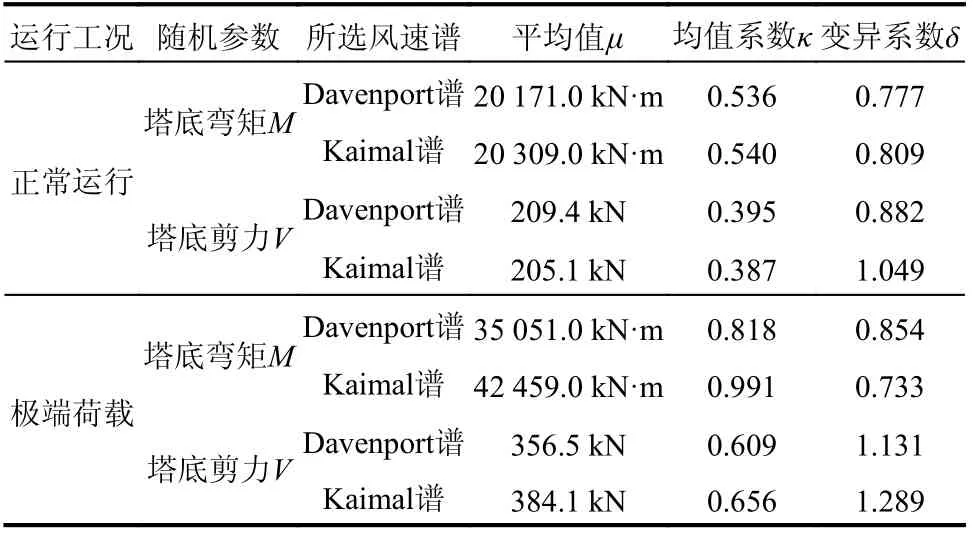
表 6 動力時程分析作用效應的統(tǒng)計參數(shù)Table 6 Statistics of load effects in dynamic time history analysis

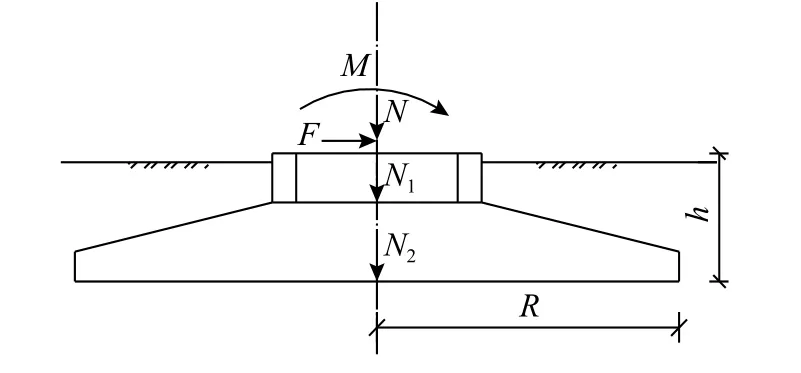
圖 9 風機基礎受力簡圖Fig. 9 Wind power foundation diagram

表 7 基礎豎向力效應統(tǒng)計參數(shù)Table 7 Statistics of vertical force effect of foundation

受各種不確定性因素的影響，偏心距e將具有較強的隨機變異性，因而存在脫開的可能。此處除考慮上部結構自重、混凝土容重、覆土容重等變量的隨機變異性外，還考慮了作用效應的隨機變異性。其統(tǒng)計參數(shù)見表8。

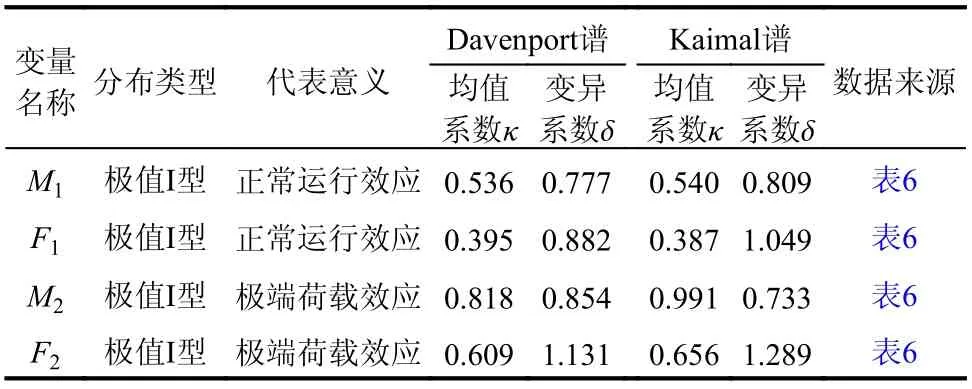
表 8 隨機變量的統(tǒng)計參數(shù)Table 8 Statistics of random variables

由于基礎脫開會造成塔筒傾覆，因此，按首超破壞準則建立失效方程。由《陸上風電場工程風電機組基礎設計規(guī)范》(NB/T 10311-2019)[27]和《高聳結構設計規(guī)范》(GB 50135-2006)[17]可知，正常運行工況下風機基礎脫開面積比不大于0，即底板偏心距e與基礎半徑R的比值不超過0.25；極端荷載工況下脫開面積比不大于25%，即底板偏心距e與基礎半徑R的比值不超過0.43。按該要求，正常運行、極端荷載工況下基礎底板脫開的極限狀態(tài)方程分別為：

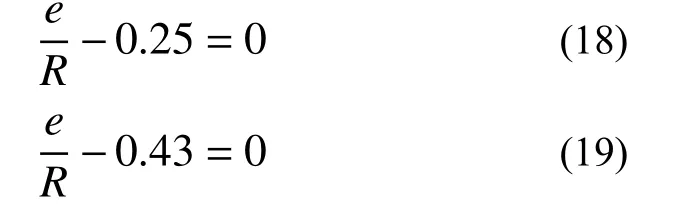
采用Monte Carlo 法，選用Davenport 譜計算得到正常運行和極端荷載工況下風機基礎底板脫開失效概率Pf分別為0.008 20 和0.0188，選用Kaimal譜計算得到的對應Pf分別為0.0107 和0.0281。

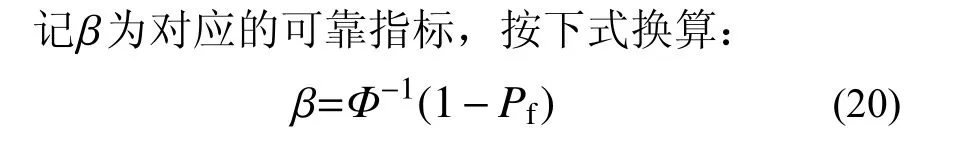
則選用Davenport 譜時兩種工況下風機基礎底板不脫空失效的可靠指標分別為2.40 和2.08，而選用Kaimal 譜時可靠指標分別為2.30 和1.91。

3.3 底板半徑變化時基礎不脫開失效的可靠度

從式(18)、式(19)可知，底板半徑對基礎底板不脫開失效的可靠度影響較大。為此，研究底板半徑變化時風機基礎底板可靠度，計算結果見表9、表10。記 η表示風機基礎底板不脫開失效的可靠指標的變化的程度：

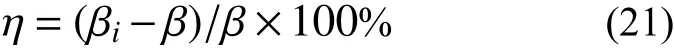
式中， βi為第i種基礎底板半徑下基礎底板不脫開失效的可靠指標。

表 9 正常運行工況下風機基礎底板不脫開失效的可靠指標Table 9 Reliable indicators without failure of wind turbine foundation slab void under operation condition

表 10 極端荷載工況下風機基礎底板不脫開失效的可靠指標Table 10 Reliable indicators without failure of wind turbine foundation slab void under extreme load condition

結果表明：兩種工況下底板半徑對基礎底板不脫開失效的可靠度的影響的確較大。當將底板半徑降至0.8 倍時，正常運行工況下按Davenport譜和Kaimal 譜計算得到的可靠指標分別降低約44.58%和44.78%，極端荷載工況下分別降低約40.87%和45.03%。當半徑增加至1.2 倍時，可靠指標均會有較大的(不小于39.90%)提升。例如，對于正常運行工況，按Davenport 譜計算得到的可靠指標提升為3.41，提高約42.08%，按Kaimal 譜計算得到的可靠指標提高約46.09%。

4 結論

本文以某3WM 風力發(fā)電高塔系統(tǒng)為結構模型，考慮脈動風場和重力二階效應，進行動力時程分析，明確其受力情況；并考慮基礎底板半徑參數(shù)的變化，對比兩種風速工況下基礎底板不脫開失效的可靠度。主要結論如下：

(1)受風機氣動力、風荷載動力效應及重力二階效應的影響，無論是在正常運行工況還是在極端荷載工況下，該3 MW 風機鋼塔筒底部彎矩、剪力等作用效應的變異系數(shù)均較高。

(2)對于文中的3 MW 風機鋼塔筒模型，當以規(guī)范中建議的基礎底板脫開面積比限值為極限狀態(tài)，選用Davenport 譜計算得到正常運行和極端荷載工況下基礎底板不脫開失效的可靠指標分別為2.40 和2.08，選用Kaimal 譜時對應的可靠指標分別為2.30 和1.91。

(3)基礎底板半徑對基礎底板不脫開失效的可靠度有較大影響，在兩種工況下風機基礎底板不脫開失效可靠指標隨著底板半徑的增大而提高。