基于骨架提取的拓撲優(yōu)化最小尺寸精確控制

閆曉磊，陳佳文，張樹忠，張 勇，黃曉東

(1. 福建省汽車電子與電驅動重點實驗室(福建工程學院)，福建，福州 350118；2. 華僑大學機電及自動化學院，福建，廈門 361021；3. 澳大利亞斯威本科技大學科學、工程與技術學院，維多利亞，Hawthorn 3122)

經過近幾十年的發(fā)展，拓撲優(yōu)化已經廣泛應用于航天航空、機械工程、海洋工程等領域[1-3]。但拓撲優(yōu)化得到的結構幾何形狀往往比較復雜，常用的制造工藝難以加工或成本太高[4-5]，因此，研究協(xié)同考量制造工藝約束的結構設計方法具有明顯的工程實際意義。

在結構設計中，極限尺寸是一類重要的制造約束。比如構件的最小、最大尺寸以及孔洞的最小尺寸控制等。考慮尺寸約束是結構拓撲優(yōu)化領域的一個難點，近年來，國內外學者在這方面做了一些工作。

Poulsen[6]引入非負函數(shù)MOLE，對特定方向上的密度梯度施加約束，實現(xiàn)了最小尺寸控制。Guest 等[7]以節(jié)點密度為設計變量，通過調節(jié)節(jié)點到單元的映射半徑，實現(xiàn)拓撲結構的最小尺寸控制。類似地，白偉等[8]通過懲罰映射區(qū)域的單元平均密度，達到了控制結構最大尺寸的目的。Zhou 等[9]在三重密度場(設計密度、濾波密度、映射密度)框架下，通過聯(lián)合調節(jié)濾波半徑、映射閾值及其范圍，提出了一種可調控最小尺寸的拓撲優(yōu)化方法。采用類似的處理方法，Dunning[10]將其引入基于參數(shù)化隱式函數(shù)的拓撲優(yōu)化方法，實現(xiàn)了最小尺寸控制。以上研究通過對設計變量施加約束，間接地隱式地實現(xiàn)了最小尺寸控制，但往往無法實現(xiàn)特征尺寸的精確控制[11]。

Zhang 等[12]基于SIMP(Solid Isotropic Material with Penalization)拓撲優(yōu)化方法，借助于拓撲結構骨架實現(xiàn)了最大、最小尺寸的精確控制；Guo 等[13]基于水平集方法，利用符號距離水平集函數(shù)提取了拓撲結構的骨架，并通過約束其極值，實現(xiàn)了拓撲結構的最大、最小尺寸控制；Niu 等[14]基于MMC(Moving Morphable Components)方法，通過在組件的寬度上施加相同的上限和下限，實現(xiàn)了結構的等尺寸控制；Liu[15]基于水平集方法，通過對拓撲結構骨架的識別與分割，將拓撲結構分解為多個條狀組件，實現(xiàn)了結構的動態(tài)極限尺寸控制。以上研究，借助拓撲結構的骨架，顯式地實現(xiàn)了結構特征尺寸的精確控制，但這些方法難以考慮骨架變化對設計變量靈敏度的影響[16]。

漸進結構優(yōu)化方法(Bi-directional Evolutionary Structural Optimization, BESO)是一種啟發(fā)式的拓撲優(yōu)化方法，具有原理簡單、效率高、易實現(xiàn)的特點[17-18]。因此，本文嘗試以BESO 方法為基礎，通過細化邊界單元及提取拓撲結構骨架，提出一種高效的拓撲優(yōu)化方法，避免繁瑣的公式推導的同時，實現(xiàn)最小尺寸的精確控制。

1 BESO 算法改進

BESO 拓撲優(yōu)化方法，雖然具有效率高、原理簡單的優(yōu)點，但優(yōu)化結果存在鋸齒狀邊界問題[19]，無法直接用于CAD 幾何建模，也不利于特征尺寸的控制。對此，本文首先對傳統(tǒng)BESO 方法進行改進。

1.1 拓撲優(yōu)化模型

以最小化結構平均柔度為目標為例，拓撲優(yōu)化模型可定義為：

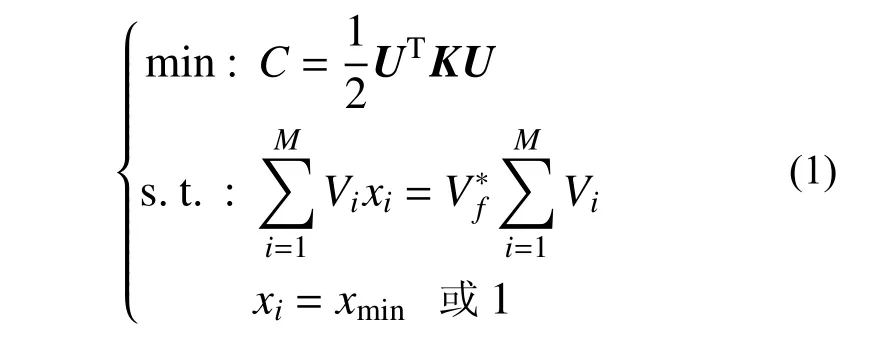
式中：xi為第i個單元的拓撲設計變量，當xi=1 表示該單元為實單元，當xi=xmin表示該單元為空單元(為避免求解困難，xmin通常取接近于零的小值，本文xmin取10-3)；C為結構的平均柔度；U為節(jié)點位移向量；K為整體剛度矩陣；Vf*為目標體積分數(shù)；Vi為單元i的面積或體積；M為設計域單元總數(shù)。

1.2 靈敏度分析及單元濾波

在BESO 算法中，仍然采用SIMP 插值模型，即第i個單元的彈性模量可表示為：

式中：E0為基體材料的彈性模量；p為懲罰因子(本文取3)。

根據目標函數(shù)式(1)，再結合插值模型式(2)，可求得目標平均柔度C對拓撲設計變量xi的偏微分為：

有了靈敏度分析式(3)，單元敏度數(shù)可以定義為：

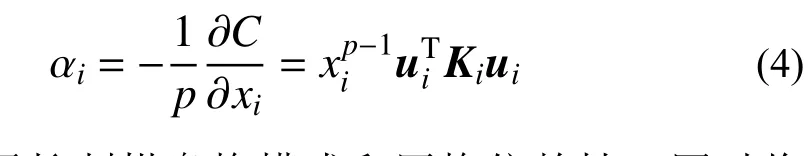
為了抑制棋盤格模式和網格依賴性，同時將單元敏度數(shù)轉化為節(jié)點敏度數(shù)，這里采用權重濾波方法[20]：

式中：rmin為過濾半徑；rji為節(jié)點j和單元i中心的距離。

1.3 邊界單元細化

為了得到光滑的邊界，通常的做法是加密有限元網格，但網格增加勢必會造成計算量的急劇增加。本文采用形函數(shù)插值方法，對結構拓撲邊界上的單元進行虛擬細化，在不增加有限元網格的情況下，達到光滑結構拓撲邊界的目的。下面給出具體細化過程。

首先，將結構邊界上的某個單元劃分為Ne個小單元(該小單元并不參與有限元計算)，則第k個小單元的靈敏度可由該邊界單元的節(jié)點靈敏度計算得到：

在優(yōu)化過程中，并不是所有單元都進行上述細化處理，而僅細化結構拓撲邊界上的單元。判斷單元是否是邊界單元，要根據節(jié)點靈敏度的大小排序確定，即邊界單元的節(jié)點靈敏度滿足：

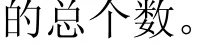
2 拓撲結構骨架提取及最小尺寸控制

2.1 骨架提取算法

圖形骨架具有中心性、同倫、單位性且不會改變原圖形的拓撲特性。因此，采用骨架對尺寸精確定義以及控制具有明顯優(yōu)勢。本文所采用拓撲細化算法[22]來提取拓撲結構骨架。

拓撲細化算法的核心就是逐層刪去結構邊界上的簡單點(Simple point)，所謂簡單點就是刪除之后不改變圖形拓撲特征的點。在有限元框架下，若某邊界實單元v滿足下面的公式，則視該單元為簡單點[23-24]：

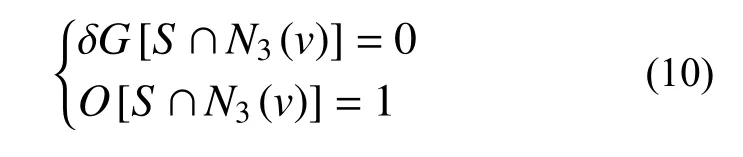
式中：N3(v)為單元v的26 個鄰域單元，即3×3×3基體，如圖1 所示；δ 為變量的改變；G為該單元基體N3(v)的歐拉示性數(shù)；O為基體N3(v)的連接體數(shù)；S為實體單元。若第一式成立表示該單元滿足歐拉特性；若第二式成立表示刪除該邊界單元后連通性不改變。

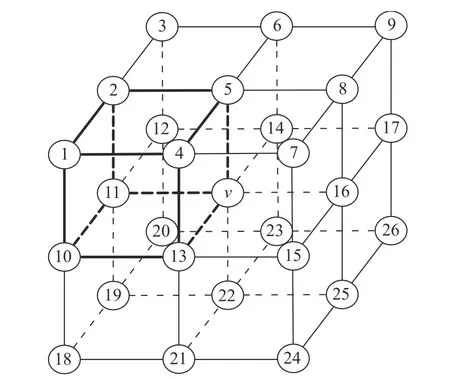
圖 1 N2(v)和N3(v)基體Fig. 1 Frameworks for N2(v) and N3(v)

在實際操作中，第一步是選出設計域的邊界，若N3(v)的26 鄰域單元中只有一個實單元，則單元v為邊界點中的端點，直接保留，繼續(xù)第二步。

第二步驗證歐拉特性。將3×3×3 基體N3(v)劃分為8 個2×2×2 基體N2(v)，則單元v的歐拉特性可計算為[25]：

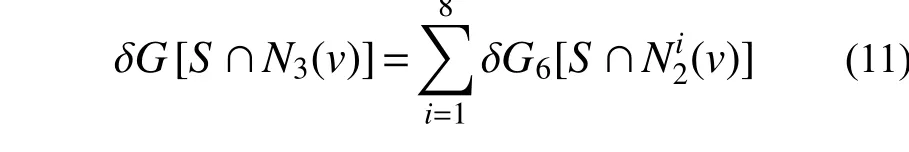
式中，G6為單元v的6 鄰域歐拉特性，在第i個N2(v)基體中，單元v的6 鄰域歐拉示性數(shù)的變化量可計算為：

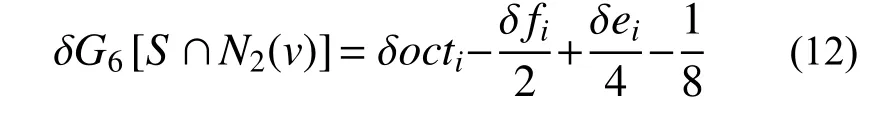
式中，ei、fi、octi分別為單元i所在N2(v)基體中實單元所形成的邊、面和基體的數(shù)目。

第三步驗證連通性。可采用八叉樹算法[26]，計算邊界實單元v的連接體數(shù)，若計算得到的連接體數(shù)為1，同時邊界單元v刪除時式(11)為0，則該單元為簡單點，直接刪除，否則，保留。

2.2 骨架毛刺去除

利用第2.1 節(jié)過程，可提取到每一步優(yōu)化后拓撲結構的骨架，但在拓撲結構邊緣處的骨架可能會生成毛刺[27]，使骨架形狀失真。因此，在得到拓撲結構骨架后，還需要進行去毛刺處理。去除毛刺的原理比較簡單，若骨架端點到連結點的長度小于閾值Lth，即認為該骨架分支為毛刺，進行刪除。需要注意的是，在去除毛刺時，可能會將原連結點轉變?yōu)樾碌亩它c，從而產生新的毛刺，因此，毛刺的去除須分級去除，直到無毛刺可去除。本文毛刺閾值Lth取10 個單元的長度。

2.3 最小尺寸控制

在迭代過程中，得到拓撲結構的骨架單元后，以最小控制尺寸dmin為直徑，以骨架單元的形心為球心，掃掠整個骨架，即可確定最小尺寸對應的控制域B(dmin)。在優(yōu)化過程中，始終保證形心在控制域B(dmin)內的單元全部為實單元，從而實現(xiàn)拓撲結構最小尺寸的精確控制。

此外，需要說明的是，拓撲優(yōu)化過程中，拓撲構型的演化是通過空洞的生成與合并形成的，如果直接施加最小尺寸約束，可能會造成優(yōu)化結果早熟[12]，得不到最優(yōu)解。為避免這一現(xiàn)象，本文采用逐漸強化約束的方法，即構造最小尺寸約束為：

3 拓撲優(yōu)化最小尺寸控制算法步驟

根據上面分析，基于BESO 的最小尺寸控制拓撲優(yōu)化算法可概括為以下步驟：

步驟1：設計域網格離散，初始化設計參數(shù)：收斂精度ε、目標體積分數(shù)Vf*、進化率ER、過濾半徑rmin及最小尺寸dmin等；

步驟2：對結構進行有限元方法分析，根據式(3)分析目標函數(shù)的單元靈敏度；

步驟3：根據式(5)計算節(jié)點靈敏度；

步驟4：確定當前迭代步材料目標體積分數(shù)：

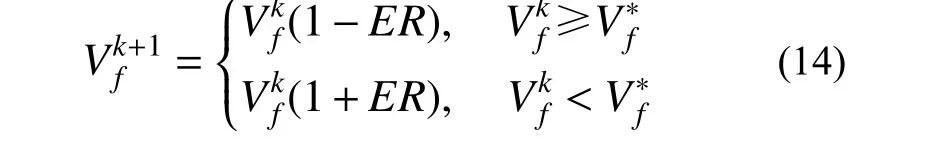
步驟5：節(jié)點靈敏度排序，細化邊界單元；

步驟6：單元(包括小單元)刪、添；

步驟7：提取拓撲結構的骨架；

步驟8：根據式(13)，確定控制域B(dmin)，施加最小尺寸約束；

步驟9：更新結構；

步驟10：返回步驟2，直到滿足體積約束和目標函數(shù)收斂精度。

4 實例分析

下面通過實例來驗證所提出的最小尺寸控制拓撲優(yōu)化算法。為簡化起見，以下所有實例中，材料的彈性模量和泊松比都分別取為E=1 GPa、ν=0.3；進化率ER=0.01；另外，二維單元細化規(guī)模為10×10 個小單元、三維單元細化規(guī)模為10×10×10 個小單元。

4.1 算例1. L 型梁結構

首先，為驗證算法的有效性，對于如圖2 所示L 型梁結構，右端中點受大小為1 kN 的集中載荷作用，上邊界固支；初始設計域被離散為5120 個矩形有限元網格；過濾半徑rmin=2 mm，最小控制尺寸為dmin=2 mm。

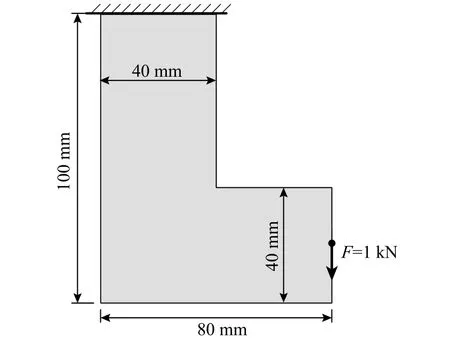
圖 2 L 型梁結構設計域Fig. 2 Design domain of a L-shape beam

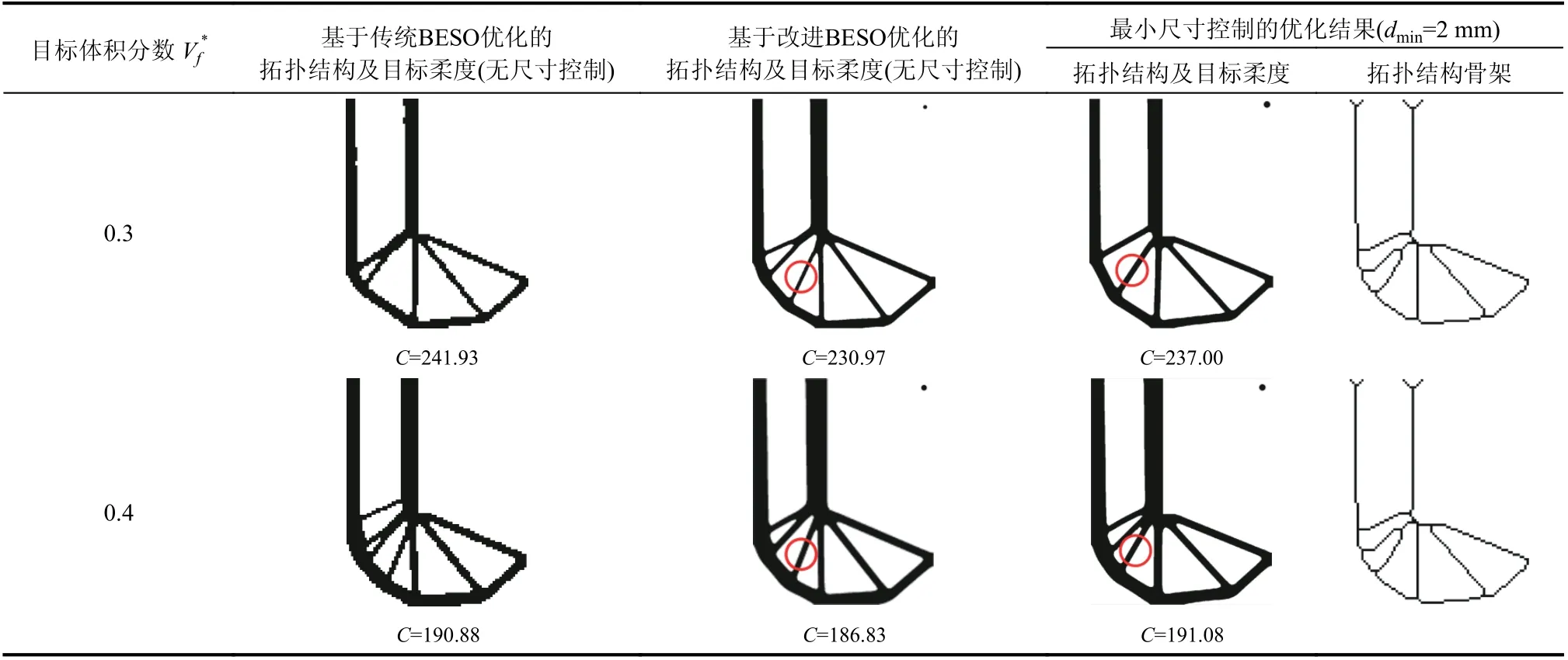
表 1 L 型梁不同體積分數(shù)下的最小尺寸控制優(yōu)化結果Table 1 The optimized results with minimum length scale control under different volume fractions for the L-shape beam

圖3 給出了表1 對應的最小尺寸約束下不同目標體積分數(shù)約束時的目標函數(shù)收斂曲線。優(yōu)化過程體積分數(shù)逐漸減少到目標體積分數(shù)，目標柔度逐漸增大直至收斂，收斂過程十分平穩(wěn)。

4.2 算例2. 懸臂梁結構

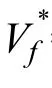
先來研究最小尺寸約束施加過程，即參數(shù)β 的影響，此時固定最小尺寸約束為dmin=2 mm。圖5 對比了β=5、β=10、β=20 情況及無尺寸約束的優(yōu)化結果。從圖5 中可以看出，最小尺寸約束的施加對優(yōu)化結果具有顯著的影響。β 較小時，由于整個優(yōu)化過程最小尺寸約束都在起作用，此時優(yōu)化得到的拓撲結構中存在很多桿件，并且目標柔度變大(相對于無尺寸約束情況)；隨著β 的增加，最小尺寸約束相當于施加在優(yōu)化過程的后期，此時拓撲結構中桿件逐漸變少，結構趨于簡化，目標柔度也逐漸接近無尺寸約束情況。事實上，在拓撲構型演化中，空洞的生成與合并過程也就是最小尺寸“桿件”的產生與斷裂過程，最小尺寸約束的施加勢必會影響這一過程，造成優(yōu)化過早收斂[10,12]，而通過松弛施加最小尺寸約束可以有效避免這一問題。

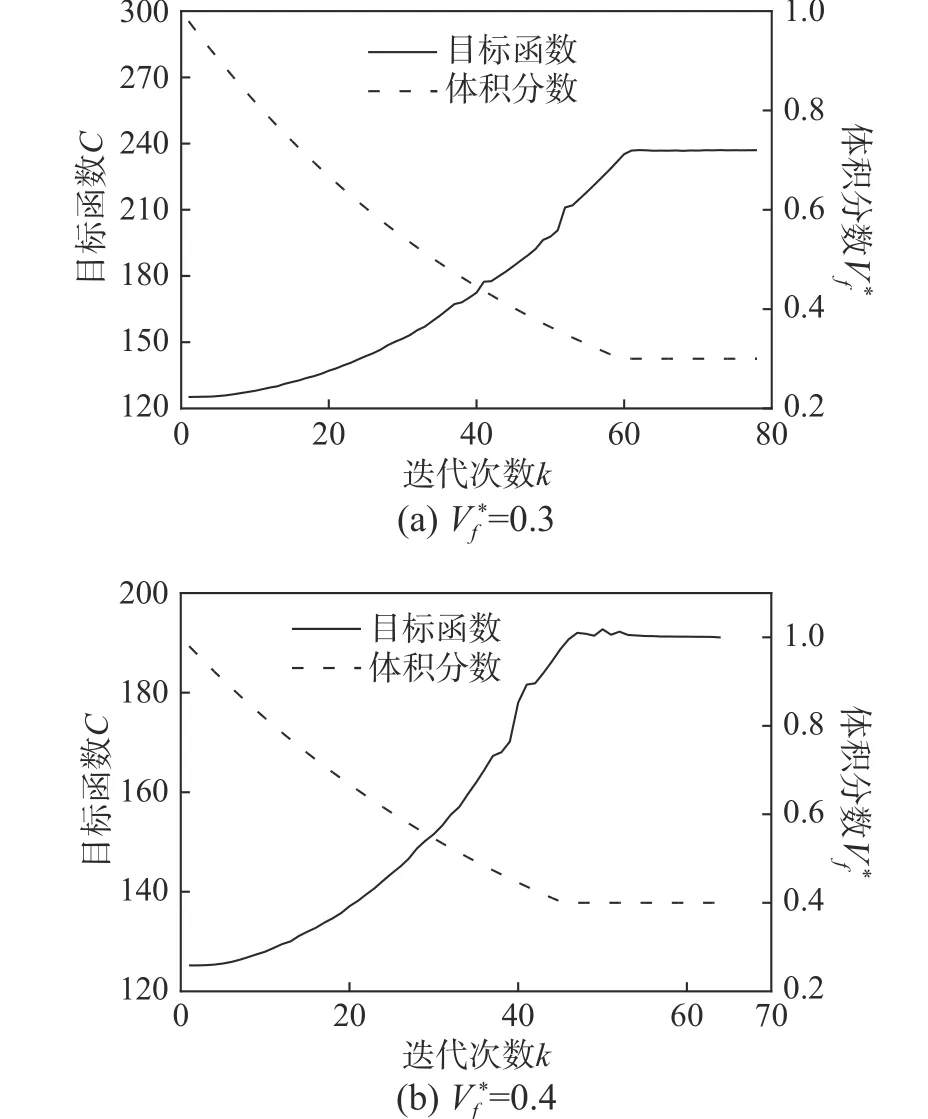
圖 3 最小尺寸控制下的目標柔度及體積分數(shù)迭代曲線 (dmin=2 mm)Fig. 3 Iterative history curves of the objective compliance and the volume fraction with the minimum length scale control (dmin=2 mm)

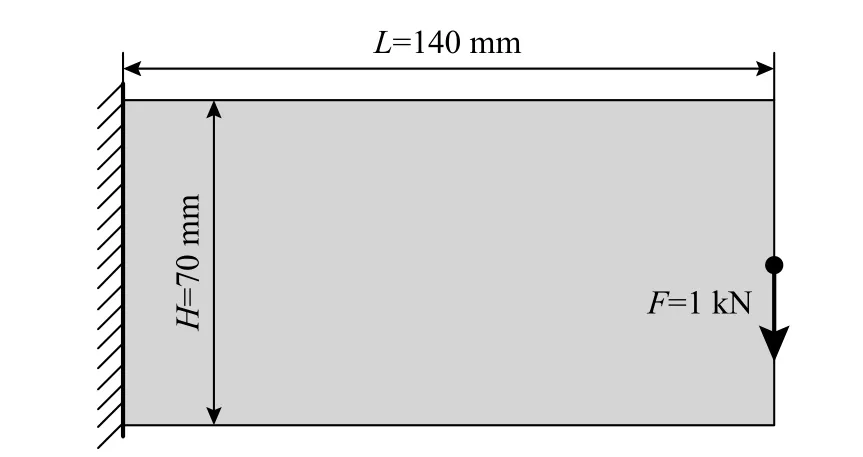
圖 4 懸臂梁設計域Fig. 4 Design domain of the cantilever beam

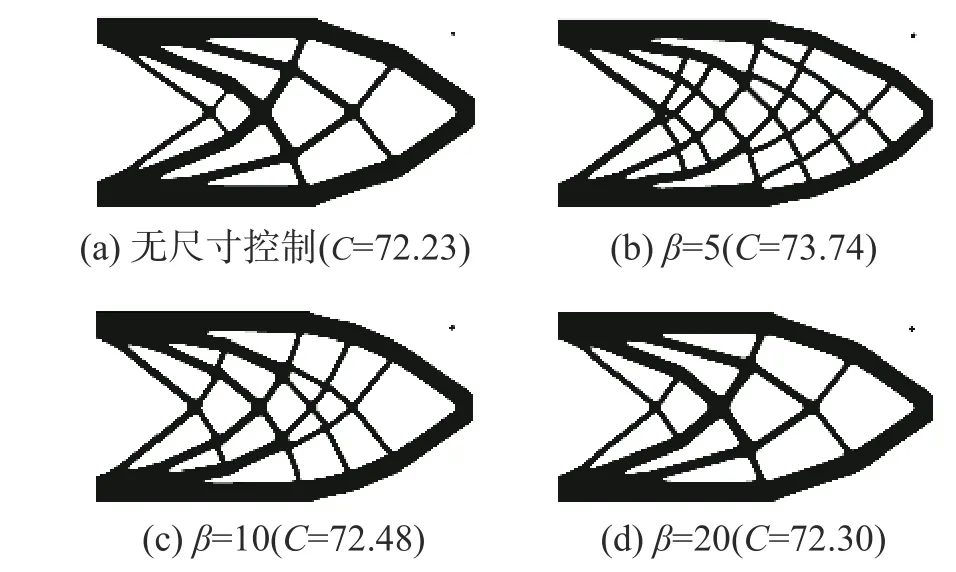
圖 5 不同β 值的拓撲優(yōu)化(dmin=2 mm)Fig. 5 Topology optimization results with different index β (dmin=2 mm)

下面研究最小控制尺寸dmin對結果的影響。圖6 對比了最小尺寸分別為dmin=2 mm、dmin=2.5 mm、dmin=3 mm 及無尺寸約束情況下的拓撲優(yōu)化結果，此時，β 設定為20。從圖6 中可以看出，隨著最小控制尺寸dmin的增大，結構中的最細桿件逐漸變粗，并且都滿足了最小尺寸控制要求；但隨dmin的增大，結構拓撲變得復雜，目標柔度也逐漸增大；可見，最小控制尺寸dmin的大小對優(yōu)化結果具有顯著的影響，設置最小控制尺寸可以避免細小支桿的產生，提高結構的穩(wěn)定性，但過大的最小控制尺寸可能使設計結果性能變差且結構復雜。

4.3 算例3. 三維支座

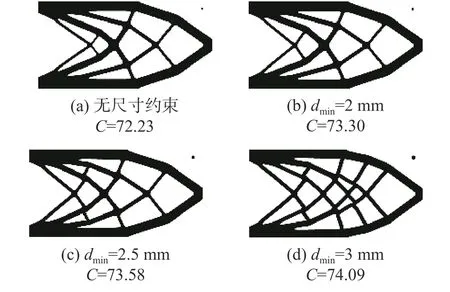
圖 6 不同最小尺寸約束的拓撲優(yōu)化結果Fig. 6 Topology optimization results under different minimum length scale controls

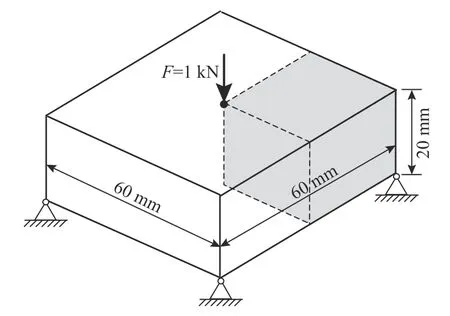
圖 7 三維支座設計域Fig. 7 Design domain of a 3D support

圖8 對比了最終的拓撲優(yōu)化結果，其中圖8(a)為無尺寸控制的拓撲優(yōu)化結果；圖8(b)為施加了最小尺寸控制的拓撲優(yōu)化結果；圖8(c)為對應的拓撲骨架結構；對比圖8(a)與圖8(b)，可以看到，支座中最細桿的尺寸可以被精確控制，但施加最小尺寸控制后，結構的整體剛度略有下降(目標柔度略有上升)；圖8(d)為體積分數(shù)及目標函數(shù)收斂曲線，從圖中可以看出，施加最小尺寸控制后，迭代收斂過程依然很平穩(wěn)。

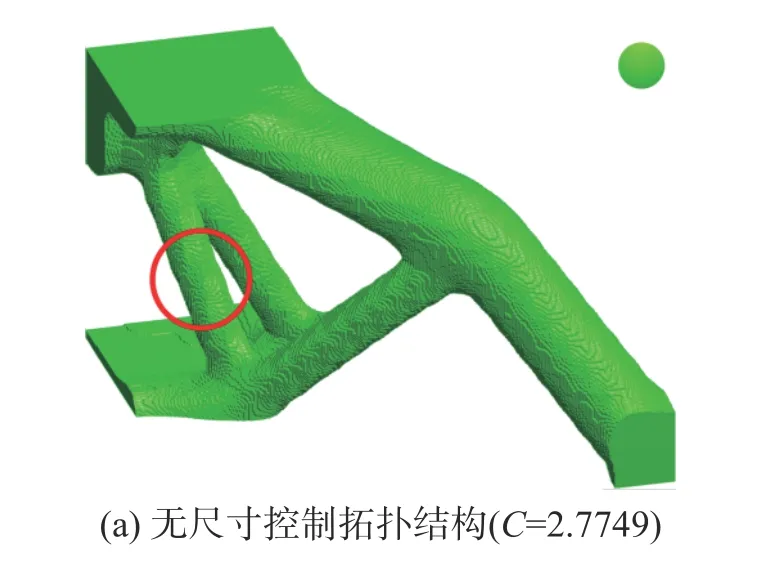
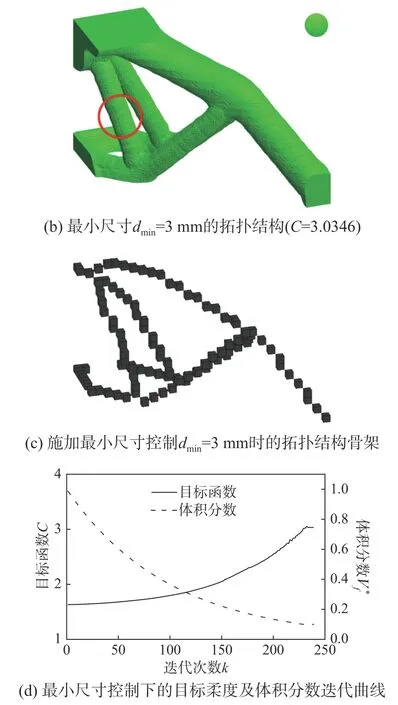
圖 8 三維支座施加最小尺寸控制的拓撲優(yōu)化結果Fig. 8 Optimized results with minimum length scale control for the 3D support

5 結論

本文在改進BESO 算法的基礎上，通過提取拓撲結構的骨架，提出了一種可控制最小特征尺寸的拓撲優(yōu)化方法。二維和三維算例表明：

(1) 該方法可以顯式地實現(xiàn)結構最小尺寸精確控制；

(2) 合理地設置最小控制尺寸可以避免結構產生細小支桿，提高結構的穩(wěn)定性，但過大的最小控制尺寸會使結構變得復雜且性能變差；

(3) 最小尺寸約束的施加對拓撲構型演化過程影響顯著，本文通過最小尺寸約束松弛施加的方法，有效避免了優(yōu)化過程早熟的問題。

在后面工作中，作者將進一步對拓撲結構孔洞尺寸及其他制造工藝約束的協(xié)同控制進行研究。