INS/GNSS/ODO 嵌入式系統的容錯技術研究
(武漢大學衛星導航定位技術研究中心,武漢 430079)
0 引言
在嵌入式組合導航系統中,傳感器短時間的故障對系統穩定性有很大影響.自適應卡爾曼濾波可在全球衛星導航系統(GNSS)定位精度突變的情況下保證定位的精度[1].而該算法是在假定只有GNSS 粗差的情況下使用的.GNSS/慣性導航系統(INS)組合導航中,傳統的χ2檢驗可以判斷出系統是否存在故障,不過其不能區分出故障所在的傳感器[2].基于神經網絡的χ2檢驗方法和利用粒子濾波的故障檢測方法可辨別出故障傳感器[3-4].由于其計算開銷較大,并不適用于嵌入式導航系統.
在所有故障中,GNSS 故障對組合導航的性能影響最為顯著,且該故障可分為軟故障和硬故障[5-6].當GNSS 整體的可觀測性較差時,檢測靈敏度較低的殘差卡方檢驗將在GNSS 軟故障下偏離真實值[7].任旭陽[8]提出基于貫序概率比檢驗法(SPRT)的故障檢測算法對軟故障的檢出具有較好的效果,但該算法并不能對故障進行及時地隔離及糾正處理.張浩等[9]提出的雙狀態卡方故障檢測系統對具有高精度慣性測量單元(IMU)系統的GNSS 軟故障具有較好的效果,該方法并不適用于低成本IMU 組合導航系統,并且雙狀態同時面臨著INS、里程計(ODO)等故障污染的風險.
隧道、林蔭道等復雜環境下,實時動態(RTK)定位結果無法長時間保持在固定解,因此本文針對這一問題實現了基于多GNSS 狀態的INS/GNSS/ODO抗差組合導航算法,提高了系統對GNSS 狀態的容錯性.同時,在此基礎上提出了一種兩級故障檢測方法,提高了系統對各傳感器故障的容錯性.其中,第一級檢測使用了基于解析冗余[10]的殘差卡方檢驗法,可檢驗出ODO、INS 和部分GNSS 故障,并保證了第二級檢驗的狀態傳播過程不受污染.第二級檢測使用了改進的雙狀態傳播卡方檢驗算法,可用于進一步檢出GNSS 軟故障.
1 INS/GNSS/ODO 組合導航
1.1 狀態方程
INS/GNSS/ODO 松組合導航系統選取十六維向量作為系統狀態向量,
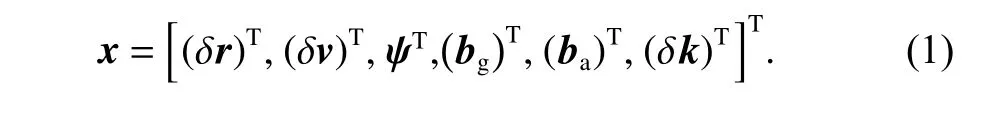
式中:δr為位置誤差;δv為速度誤差;ψ為姿態誤差;bg為陀螺儀零偏;ba為加速度計零偏;δk為里程計標度因子誤差.
系統狀態方程可表示為
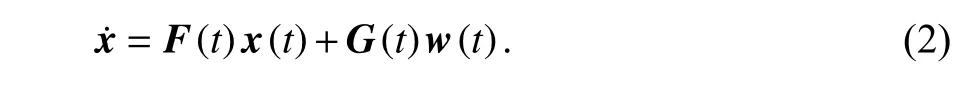
式中:F(t)為狀態轉移矩陣;G(t)為系統噪聲驅動矩陣;w(t)為系統噪聲.該系統是以GNSS、ODO 輔助INS 的形式運行的.
在式(2)中,狀態轉移矩陣推導自INS 的誤差方程,常用的有ψ 角誤差模型[11]:
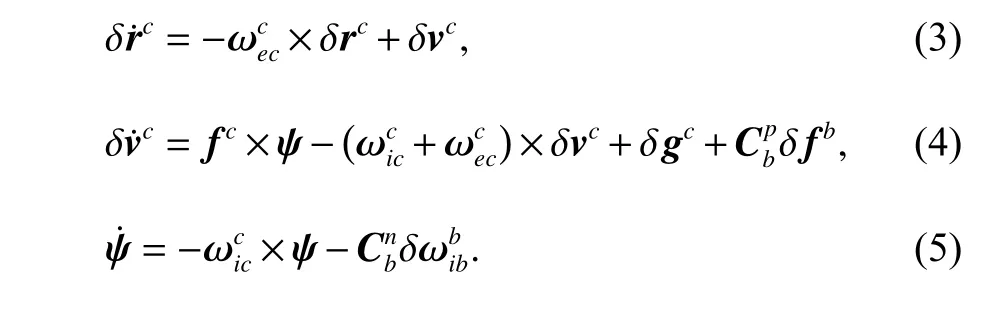
式中:f為加速度計輸出的比力;δg為重力誤差;投影坐標系b系為載體坐標系;投影坐標系c系為計算坐標系;p系為平臺坐標系;ψ 為c系到p系間的誤差角.
根據機械編排誤差模型和MEMS 的一階馬爾可夫模型可得到離散的狀態轉移矩陣,如式(6)~(8)所示[18]:

式中:RM為子午圈曲率半徑;RN為酉卯圈曲率半徑;g為當地重力;h為地理高度;?t為時間更新的時間間隔;?k/k?1為離散形式的狀態轉移矩陣;i系為地心赤道慣性系;e系為地心地固系;n系為導航系.
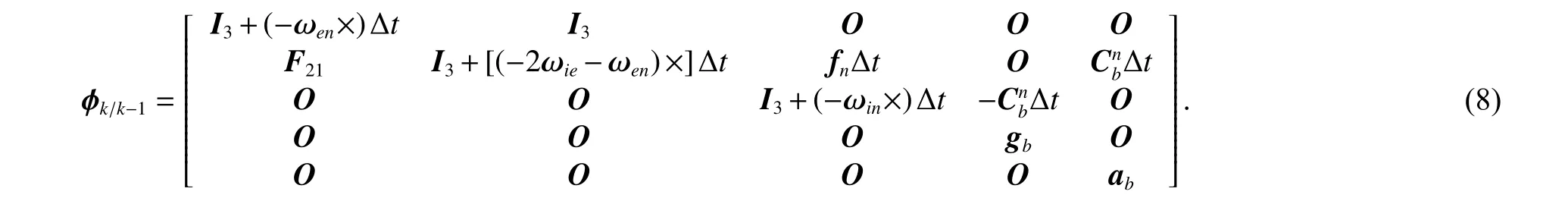
1.2 量測方程


1.3 基于多GNSS 狀態的抗差濾波
當林蔭道、隧道等復雜場景下,GNSS 信號容易受到影響,RTK 解在固定解、浮點解、抗差解和無有效解四種狀態下變化.GNSS 量測不確定協方差矩陣

式中:Ξ()函數將向量變換為對角矩陣,同時非對角線上元素全為0 的方陣;σ2為具體GNSS 狀態下的通過參數估計法獲取的三軸上協方差向量.
由于R1的不連續性,在R1從低定位精度解狀態變為低定位精度解狀態時,系統狀態量可靠性不高,系統檢出量測粗差或故障的能力差.同時GNSS 量測中存在較多的粗差,故可根據式(23)~(32)所表示的抗差濾波算法對組合時的量測不確定性進行調整[13].
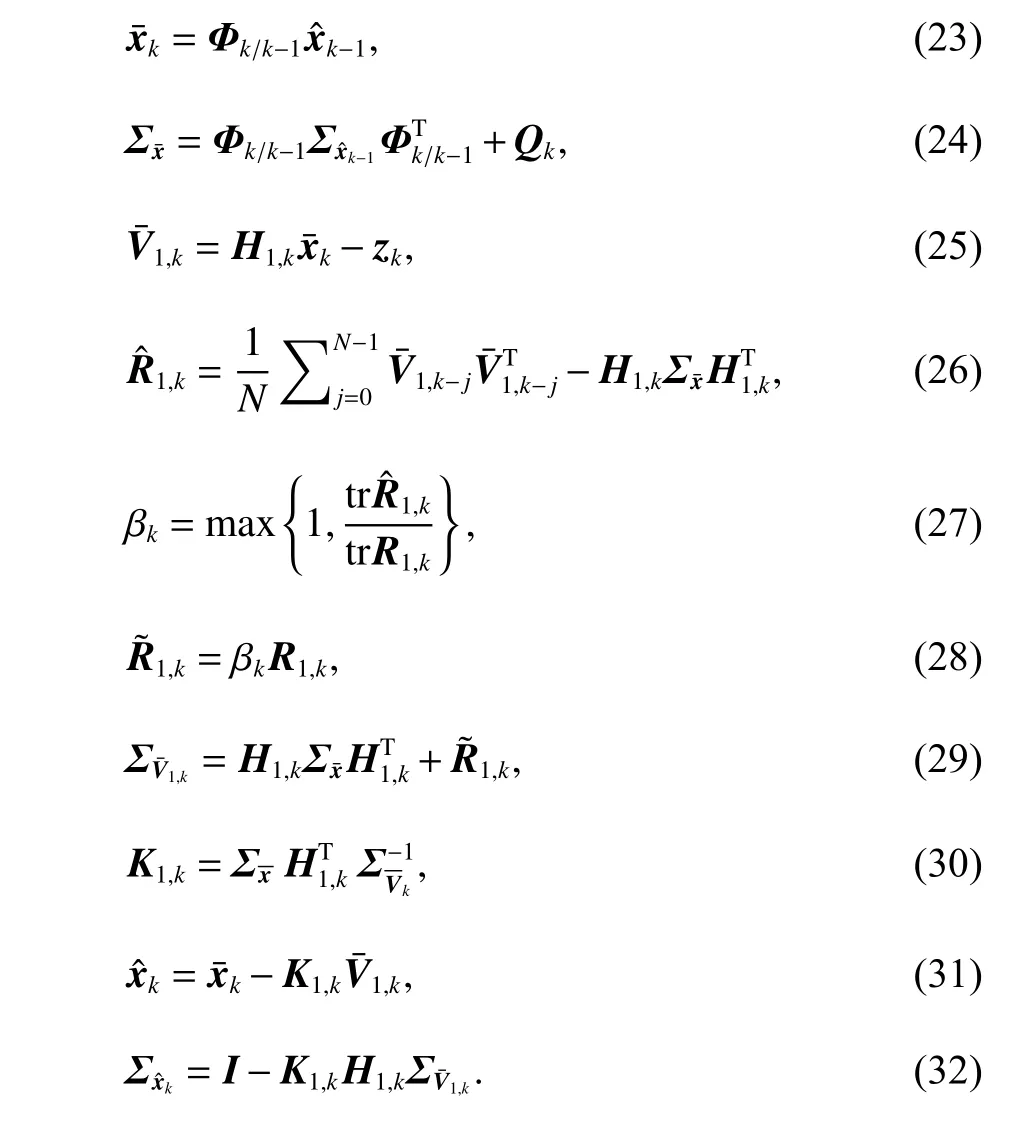
式中:Qk為系統狀態動態變化中噪聲的協方差矩陣;Ση為任意參量η的協方差矩陣;為預測殘差,又稱為新息[14];為量測不確定協防差矩陣R1,k的參數估計值;N 表示參數估計的窗口大小;βk為抗差因子;在貫序卡爾曼濾波中,下標1 特指GNSS的量測更新過程.
由于模型中錯誤地判斷GNSS 固定解將對系統的穩定性造成的影響極大,在濾波前可使用GNSS 位置精度因子(PDOP)對可疑值進行剔除.

式中:pdop為測得的PDOP 值;CBAD為給定的閾值常量.
抗差濾波算法可以降低GNSS 粗差的影響,但是在假定其僅有GNSS 異常下進行的,當ODO 異常或機械編排結果異常時,抗差濾波反而會降低組合結果的精度.同時當GNSS 在一段時間內出現偏差時,抗差的效果并不如故障檢出后將GNSS 屏蔽的效果好.
2 故障檢測系統
2.1 傳統的預測殘差卡方故障檢驗法
χ2故障檢測是一種通過判斷n維高斯分布的隨機向量的均值是否與假設一致來判斷系統是否故障的方法.根據隨機向量選取的不同,可分為基于狀態向量的χ2故障檢測和基于殘差的χ2
根據式(25)和式(29),可構造評價函數


2.2 改進的雙狀態傳播卡方故障檢驗法
如圖1 所示,雙狀態傳播χ2故障檢測器由雙狀態傳播器和卡方檢驗器組成.其中雙狀態傳播器又由兩個相互獨立的狀態傳播器及其控制開關組成,狀態傳播過程是從標準卡爾曼濾波中獨立出來的.
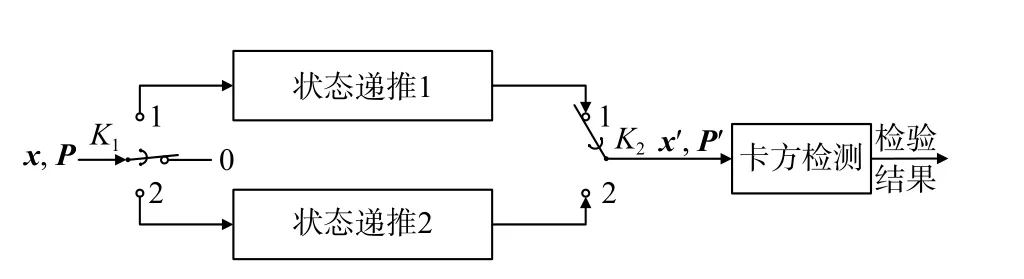
圖1 雙狀態傳播卡方故障檢測器
傳統的雙狀態傳播χ2故障檢測法一般用于具有高性能IMU 的系統中.由于消費級MEMS 的精度較差,狀態傳播的誤差呈指數增長,導致故障檢出率比傳統的殘差χ2故障檢測法差.針對這一問題,如圖2所示,本文在狀態傳播器后增加了ODO 量測更新單元,使狀態遞推的誤差在一定時間內呈線性增長趨勢.

圖2 改進的雙狀態傳播器
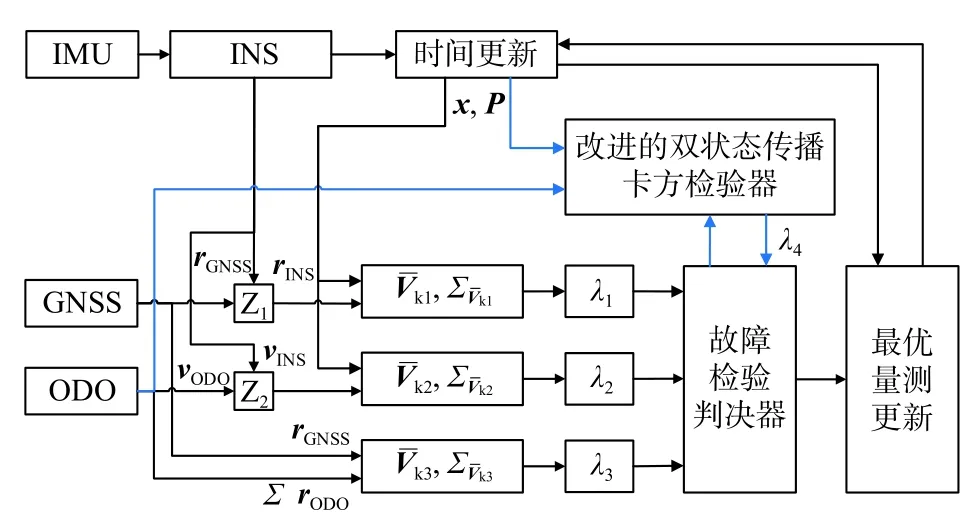
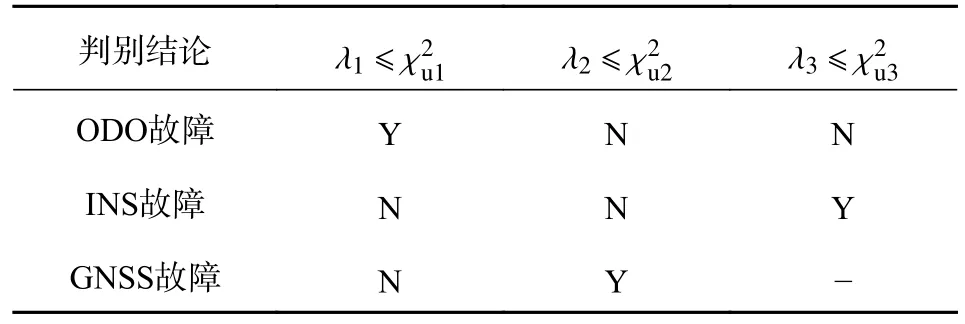
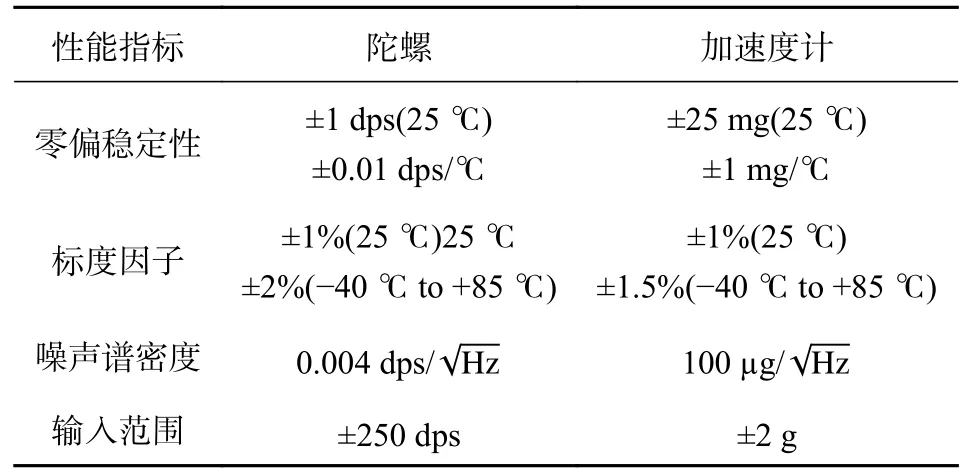
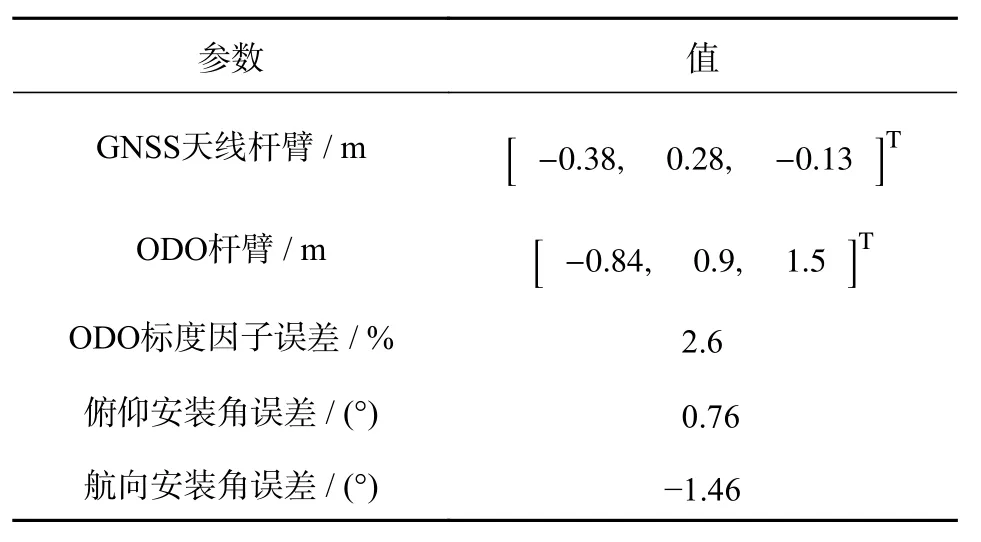
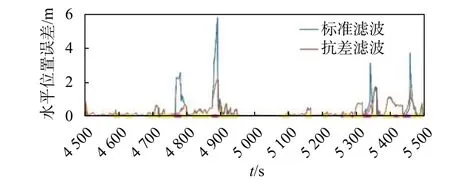
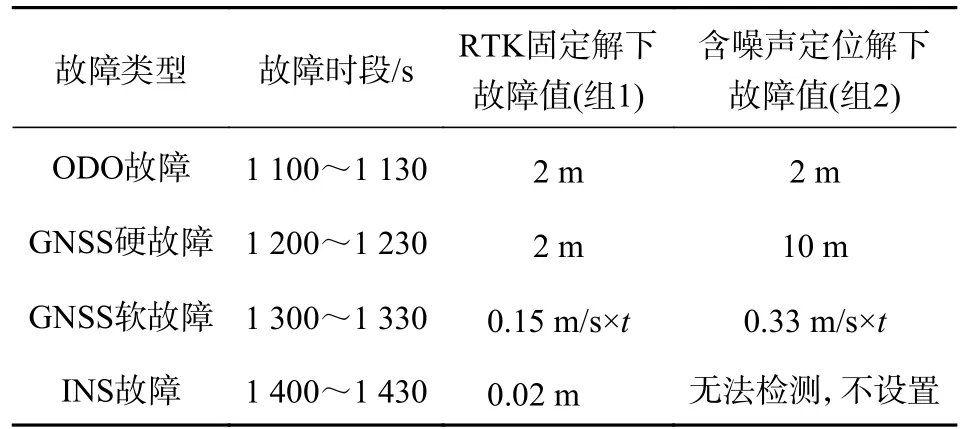
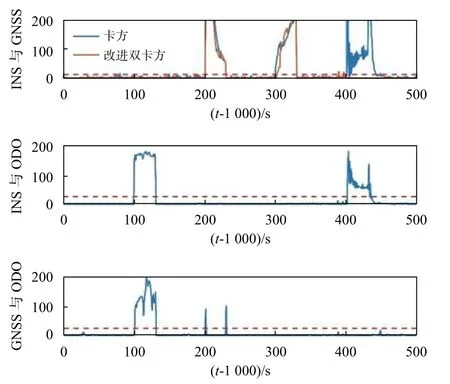
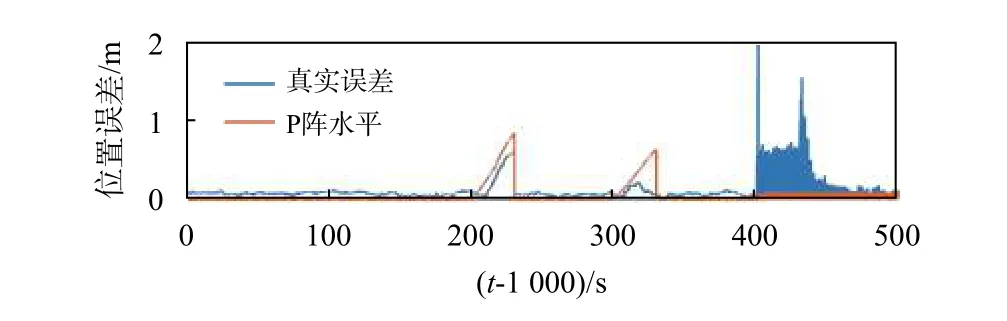
為了理論驗證改進算法的有效性及適用范圍,以單軸線性軟故障為例,當故障發生時GNSS 立即屏蔽.并假設線性軟故障增長率為a,各軸的狀態遞推誤差增長率均為b(b 可化簡為 上述的兩種方法可以用于檢測系統是否故障,但嚴格意義上并不能鎖定故障的出現位置.另一方面,雙狀態傳播卡方故障檢測法雖然能夠處理GNSS 軟故障,但其同時面臨著ODO 故障或INS 故障污染的風險.相較于不使用該方法,當ODO 故障或INS 故障發生時,系統將變得更不穩定[17]. 針對上訴兩個問題,本文提出了一種兩級故障檢測系統,如圖3 所示.在第一級檢測中,系統分別計算出三組新息及卡方值,并在故障檢測判決器中通過基于解析冗余的故障檢測方法來初步鎖定故障位置.當系統認為第一級檢測并不足以檢測出GNSS 軟故障時,系統將通過改進的雙狀態傳播卡方故障檢測法進行進一步判斷. 圖3 基于解析冗余的故障檢測系統模型 由式(37)可知,GNSS 量測的精度遠大于INS/ODO 航跡推算的位置精度,第二級檢測將被跳過,故可根據RTK 定位是否為固定解設計如表1和表2 所示. 在故障處理方面,當GNSS 故障出現時,系統屏蔽GNSS 量測更新.當ODO 出現故障時,系統屏蔽包含改進的雙狀態傳播χ2故障檢測器在內的ODO 量測更新,同時不對ODO 標度因子進行反饋和修改.當INS 發生故障時,系統將對改進的雙狀態傳播χ2器重置及屏蔽處理,防止狀態傳播器內的狀態受到污染,同時適當調節Q 陣的自適應組合導航算法避免組合導航系統發散. 表1 RTK 固定解時的第一級故障判決表 表2 含噪定位解時的第一級故障判決表 圖4 為GN310 嵌入式系統,車載實驗的核心裝置為自主研制的一款具有通信導航一體化功能的低成本嵌入式系統—GN310.該系統通過4G通信從千尋獲取RTK 差分改正數并在內部GNSS芯片中進行單頻RTK 計算,在開闊環境下可獲取厘米級定位精度信息. 圖4 GN310 嵌入式系統 為了提高在復雜場景下的魯棒性,系統內還集成了IMU、磁力計等器件,其中IMU 的性能如表3 所示.系統通過DB9 接口接入分辨率為2000P/R 的編碼式里程計即可運行GNSS/INS/ODO組合導航算法,并實時輸出高精度強魯棒性位置速度等信息.實驗使用的參考系統為裝有光纖陀螺、雙頻RTK 的GNSS/INS 緊組合系統NovAtel CPT6.實驗過程中使用表4 中參數對組合導航原始觀測數據進行修正. 表3 IMU 性能指標 表4 修正參數 實驗時長為1 000s,INS 運算頻率100Hz,ODO 量測更新頻率10Hz,GNSS 量測更新頻率均為1Hz,平均車速為40km/h. 如圖5 所示全路段經過四次隧道,路段中存在多處林蔭道,路段中存在的3 處實為浮點解或抗差解被錯誤判為固定解的GNSS 結果.水平位置誤差如圖6所示,x軸中,黃色點表示浮點解,占總測試時長的40.6%;粉色表示抗差解,占總測試時長的3.1%.標準卡爾曼濾波下,水平位置均方根誤差(RMSE)為0.67m;多GNSS 狀態抗差濾波下,水平位置RMSE為0.42m,定位效果提升39.7%. 圖5 實驗路段 圖6 水平位置誤差與時間的關系 考慮到實測中同時可遇到多種故障的情形有限,本節選用另一組全路段固定解的數據進行半實物仿真[15].測試路段平均車速為30km/h.分階段施加ODO 故障、GNSS 硬故障、GNSS 軟故障和INS故障.如表5 所示,仿真過程分為兩組,第一組在RTK 固定解下進行,第二組在含噪聲定位解下進行.其中含噪聲定位解在RTK 固定解的基礎上各軸添加1m 高斯白噪聲來模擬. 表5 故障條件 在RTK 固定解的情況下,故障檢測值如圖7所示,故障屏蔽效果如圖8 所示,其中硬故障值與真值的差在故障區間內為常向量,而軟故障值與真值的差在故障區間內為遞增向量.根據表5 的判決條件,表中的四種故障皆能有效地辨別出.在GNSS 漸變故障時,改進雙狀態傳播卡方檢測算法與殘差卡方檢測結果接近,故嵌入式系統中可跳過雙狀態傳播卡方檢測算法的計算,實現降低計算量的目標. 圖7 RTK 固定解下的卡方故障檢測 圖8 RTK 固定解下故障屏蔽效果 在單點定位解時,標準和改進的雙狀態傳播器的窗口長度都為10s.如圖9 所示,第一層故障檢測能檢出ODO 故障.圖10 是根據先驗已知的故障時間來屏蔽GNSS 量測更新,由于低成本嵌入式組合導航系統的IMU 性能較差,故標準的雙狀態傳播卡方檢測效果較差. 圖9 含噪聲定位解下的卡方故障檢測 圖10 含噪聲定位解下根據時間屏蔽的卡方結果 在根據實際的檢測閾值處理故障時,如圖11所示,在GNSS 軟故障發生時,由于故障初期殘差卡方檢測法未能檢測出該故障,組合導航結果被拉偏.而改進的雙卡方檢測法在故障發生后的第15s 時檢測出并修復了故障,從而保證了系統的穩定性和可靠性. 圖11 含噪聲定位解下的卡方故障檢測 本文提出了基于INS/GNSS/ODO 抗差組合導航算法的兩極故障檢測方法,第一級檢測使用了基于解析冗余的殘差卡方檢測法,第二級檢測使用了改進的雙狀態傳播卡方檢測算法.相比于傳統故障檢測方法,該容錯方法能夠有效地處理ODO、INS 故障和GNSS 軟故障,提高了系統的導航性能和魯棒性.該算法除了能夠用于檢測硬件故障,同時還能夠在車輛輪胎空轉和側滑、ODO 接口接觸檢測、GNSS 防欺騙等方面起到積極作用,具有良好的工程應用意義. 致謝:西北工業大學自動化學院嚴恭敏老師和武漢大學衛星導航定位技術研究中心牛小驥團隊的討論.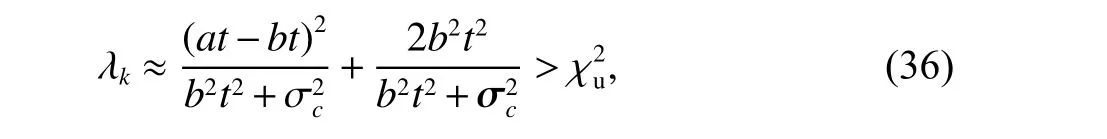
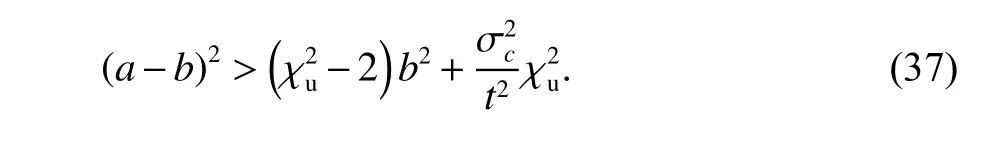
2.3 兩級故障檢測系統模型

3 實驗仿真與實驗分析
3.1 路測裝置及實驗條件

3.2 抗差組合導航的仿實時實驗

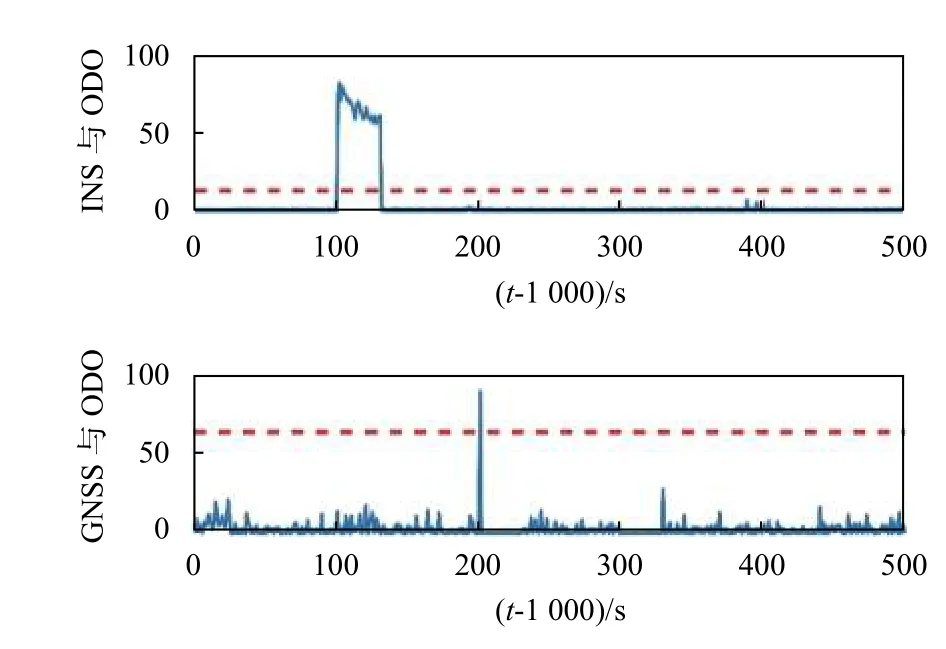
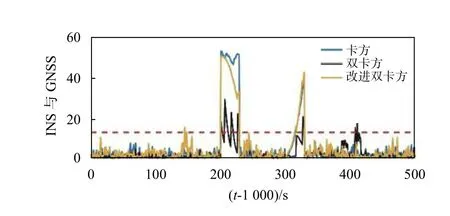
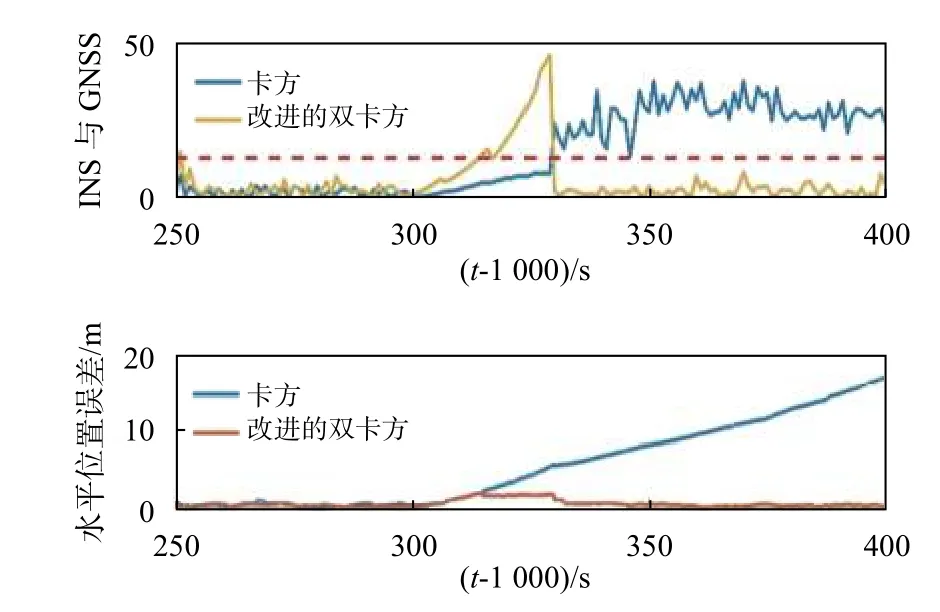
3.3 故障檢驗系統的半實物仿真
4 結束語

