神經網絡在SINS/GPS 組合定位中的應用

(東南大學 儀器科學與工程學院，南京 210096)

0 引言

在地籍測量過程中，捷聯慣性導航系統(SINS)和GPS 是兩種主要測量方式.SINS 通過安裝在載體上的陀螺儀和加速度計測量角速度和加速度，不僅可以計算出載體在參考坐標系中的相對運動，還能提供速度和姿態信息.但由于傳感器的測量誤差不斷累積，會導致SINS 的定位誤差將快速發散.GPS 可持續全天候提供高精度的位置信息，然而在實際使用過程中信號容易受到遮擋和干擾，導致不能進行定位解算.因此，對SINS 和GPS 進行數據融合，優勢互補，使融合后的定位精度高于各系統單獨工作的精度，是目前最常見的方式之一[1-2].

在SINS/GPS 組合數據融合算法中，國內外學者應用最多的是卡爾曼濾波(KF)算法以及由KF 改進的非線性濾波算法[3-4].這些濾波算法在組合導航中都有非常好的效果，然而在實際使用過程中，GPS 信號長時間失效將導致該組合方式失效，濾波器不能進行量測更新，系統進入純慣性導航模式，定位精度快速下降.近年來，以神經網絡為代表的人工智能發展迅速，神經網絡因其對非線性問題有強大的處理能力和無限逼近擬合函數等優勢，也開始廣泛應用于衛星導航領域[5].文獻[6]針對SINS/GPS 組合導航系統在GPS 信號不可用時，其定位精度產生較大退化問題，提出了遺傳算法優化的徑向基函數神經網絡(RBFNN)輔助組合導航定位的方法.為了解決因先驗知識不足而引起的濾波發散，文獻[7]和文獻[8]提出改進的RBFNN 與自適應卡爾曼濾波(AKF)或自適應無跡卡爾曼濾波(AUKF)組合算法，通過預測輸出實時估計系統噪聲參數.隨著訓練樣本的增多，RBFNN 的復雜度增大，從而運算量也增加.文獻[9]基于反向傳播神經網絡(BPNN)建立模型，模擬慣性導航系統(INS)輸出、慣性測量單元(IMU)輸出和GPS 增量之間的關系.為解決BPNN 無法處理時間序列數據的問題，文獻[10]提出一種基于循環神經網絡(RNN)的INS/GNSS 組合定位方法.但在RNN 訓練過程中，重復使用參數會導致梯度爆炸和梯度消失.文獻[11]提出一種基于長短期記憶(LSTM)神經網絡的算法輔助SINS.文獻[12]提出基于閾值濾波(EMDTF)和LSTM 神經網絡的組合濾波算法，提升了模型對時序特性的模擬能力.然而，上述算法都是在GPS 信號失效前，實時在線訓練神經網絡.在GPS 信號失效后，使用訓練好的神經網絡進行預測.訓練模型只使用了GPS 信號失效前的數據，而未使用GPS 失效后又重新恢復有效部分的數據.

為了解決地籍測量過程中GPS 信號頻繁丟失導致信號失效區域定位精度降低的問題，本文將循環神經網絡中的LSTM 神經網絡與KF 結合，根據地籍測量事后離線處理的特點，提出一種利用已有數據，使SINS/GPS 組合測量系統在GPS 信號失效區域仍能維持定位精度要求的融合算法.

1 SINS/GPS 組合定位

在SINS 中，數字平臺代替了物理平臺，陀螺儀和加速度計直接固聯在載體上.根據陀螺儀和加速度計測量得到的信息，可解算出載體的姿態、速度及位置[3,13].SINS 的姿態、速度和位置誤差方程為

式中：δVE、δVN為在東、北兩個方向上的速度誤差；ψE、ψN、ψU為在東、北、天三個方向上的姿態失準角；δL、δλ為誤差緯度和經度誤差；εx、εy、εz為陀螺儀漂移在載體坐標系中的投影；?x、?y為加速度計偏置在導航坐標系中的投影.

使用GPS 輸出的信息作為參考值，對SINS 解算的速度、位置進行修正，從而輸出高精度的定位信息.定義二維觀測向量Z為

根據SINS 的誤差模型，可以得到SINS/GPS組合定位系統的狀態方程和觀測方程為

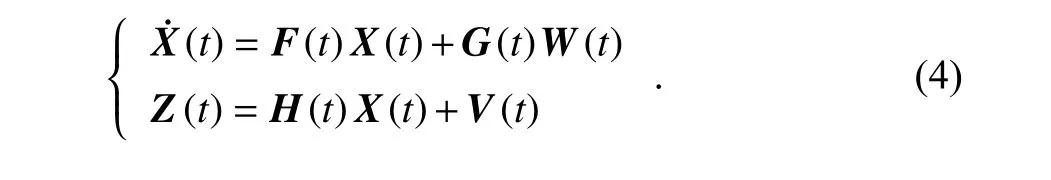
式中：F(t)為系統狀態轉移矩陣；H(t)為觀測矩陣；W(t)和V(t)分別為過程噪聲和量測噪聲.

將式(4)離散化，可得

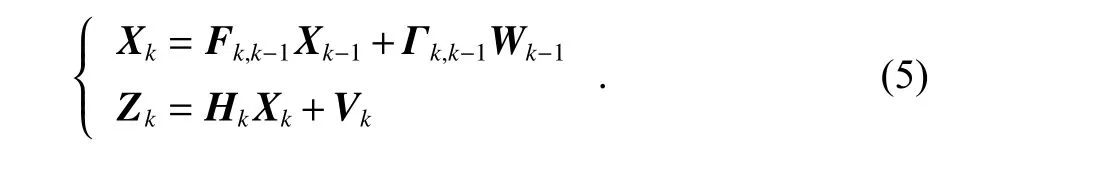
式中：Xk為k時刻n維狀態向量；Fk,k?1為系統從k?1時刻到k時刻的n×n維狀態轉移矩陣；Hk為系統k時刻的m×n維觀測矩陣；Zk為k時刻m維觀測向量；Γk,k?1為m×n維噪聲矩陣；Wk為k時刻n維過程噪聲；Vk為k時刻m維量測噪聲.Wk和Vk滿足以下統計特性

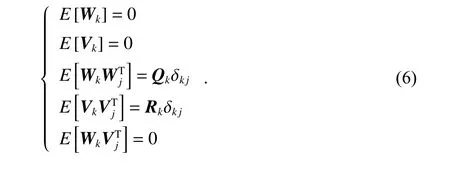
式中：Qk為系統過程噪聲Wk的非負定方差陣；Rk為系統量測噪聲Vk的對稱正定方差陣.

若已知k時刻的觀測值Zk，則狀態向量Xk和估計值可按如下規則求解

2 神經網絡模型

RNN 是一類用于處理序列數據的神經網絡，相比經典的BPNN 有非常大的提升，例如通過滑動窗口共享參數和構建長期依賴關系.此外RNN 會有一個記憶機制，即當前隱藏層的輸入不僅包含輸入層的輸出，還包括上一時刻隱藏層的輸出.而在全連接網絡中，是先輸入到隱藏層再到輸出層，層與層之間是全連接的，每層之間的節點是無連接的，所有的輸入以及輸出都各自獨立[14].RNN 的結構如圖1 所示，它有3 層，即輸入層x、隱藏層h和輸出層o.

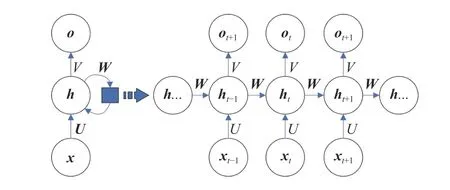
圖1 RNN 結構

RNN 從特定初始狀態h0開始向前傳播，相應的前向傳播公式為：

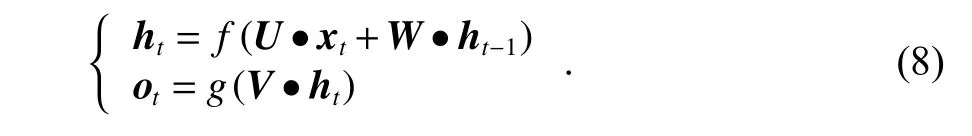
式中：xt為t時刻輸入向量；ht為t時刻隱藏層向量；ot為t時刻輸出向量；U、W、V分別為輸入權重、循環權重和輸出權重矩陣.

在RNN 訓練過程中，重復使用W、U會帶來梯度爆炸和梯度消失問題.因此，提出了LSTM 網絡，它與RNN 一樣，都是一種具有重復功能的網絡模塊，但LSTM 的內部單元進行了改進，增加了遺忘機制和保存機制[14].LSTM 網絡除了外部的RNN循環外，每個LSTM“細胞”的內部還有循環，通過反復訓練獲得網絡權重矩陣，能夠有效運用于長距離的時間序列，網絡的單元結構如圖2 所示.

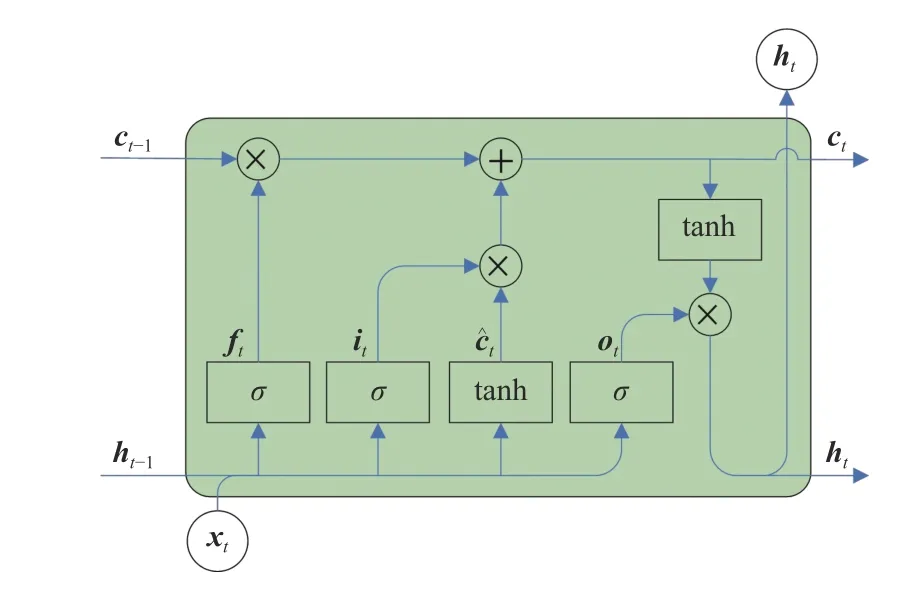
圖2 LSTM 循環網絡“細胞”

LSTM 循環網絡不是簡單地向輸入和循環單元的仿射變換之后施加一個逐元素的非線性.每個LSTM 細胞包含遺忘門Ut、輸入門it和輸出門ot，其中Ut能夠限制上一時間節點輸出的信息量，it可以選擇性地獲取新的輸入信息，ot則能根據新輸入的信息與上一時刻輸出的信息計算出當前時刻的輸出[15].相應的前向傳播公式可表示為

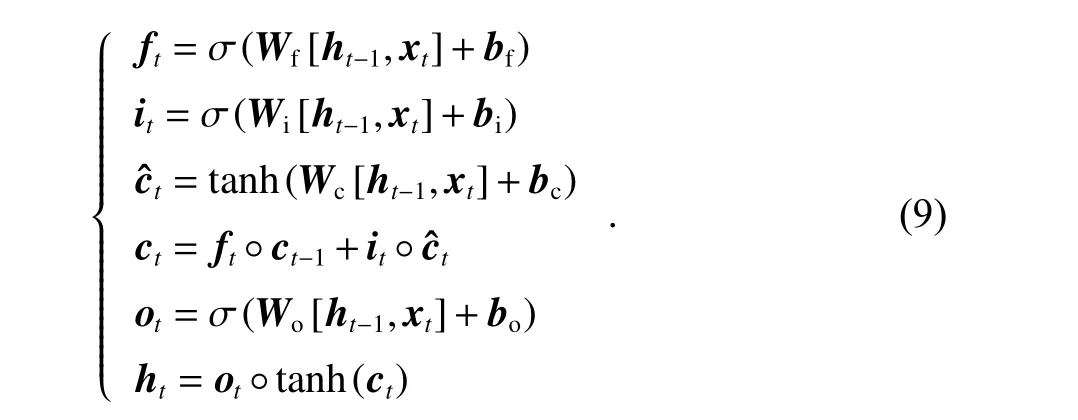
式中：bf、Wf分別為遺忘門的偏置和循環權重；bi、Wi分別為外部輸入門的偏置和循環權重；ct為神經元狀態；為候選向量；bo、Wo分別為輸出門的偏置和循環權重；?代表圈乘.

3 誤差抑制方案設計

基于神經網絡的SINS/GPS 組合定位系統的主要思想是建立模型，模擬傳感器數據和導航信息之間的關系.目前，主要有兩類不同的神經網絡模型：一類是OSINS～δPSINS?GPS模型，建立SINS 的輸出OSINS和SINS 與GPS 之間的位置誤差δPSINS?GPS的關系；另一類是OSINS～δPGPS模型，建立SINS 的輸出OSINS和GPS 位置增量之間的關系.由于OSINS～δPSINS?GPS模型同時受到SINS 誤差和GPS 誤差影響，而OSINS～δPGPS模型僅受GPS 誤差影響.因此，OSINS～δPGPS模型能夠獲得更高的預測精度.本文采用OSINS～δPGPS模型作為神經網絡訓練與預測模型.

由SINS 機械編排[3]可知，k時刻位置增量的函數可表示為

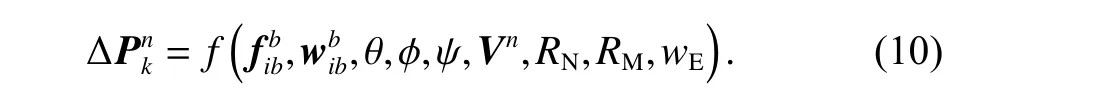
在地籍測量過程中，RN、RM和wE的變化非常小，且履帶式小車的俯仰角θ和橫滾角?的值通常也很小.因此，我們可以簡化函數，建立k時刻位置增量模型為

根據上述分析，可定義LSTM 神經網絡輔助KF 的組合定位系統結構如圖3 所示.在GPS 信號有效區域，一方面根據KF 更新式(1)～(7)對SINS 和GPS 的數據進行融合，修正SINS 解算的誤差，提高系統定位精度.另一方面，IMU 和SINS 的輸出信息作為LSTM 神經網絡模型的輸入、輸出位置增量和GPS 位置增量比較，優化模型參數，對其進行訓練，系統結構如圖3(a)所示.在GPS 信號失效區域，利用訓練得到的最優神經網絡模型，輸入IMU 和SINS的輸出數據來預測GPS 位置增量信息，對?積分可獲得偽GPS信息，從而可繼續對SINS/GPS組合定位系統中KF 進行量測更新，為SINS 的解算結果提供誤差修正，防止系統進入純SINS 模式，系統定位精度快速下降，其結構如圖3(b)所示.

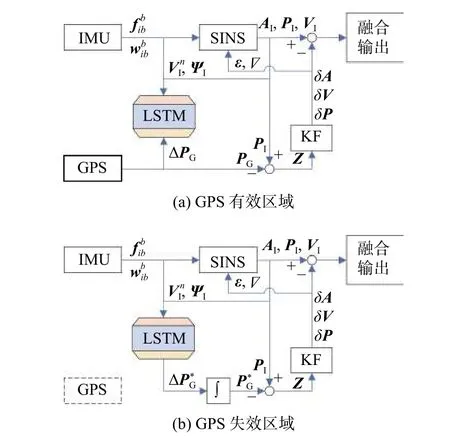
圖3 組合定位系統結構圖

4 仿真實驗與結果分析

為了驗證算法的有效性，我們結合地籍測量的特點，設計了SINS/GPS 組合定位仿真實驗，運動軌跡如圖4 所示.

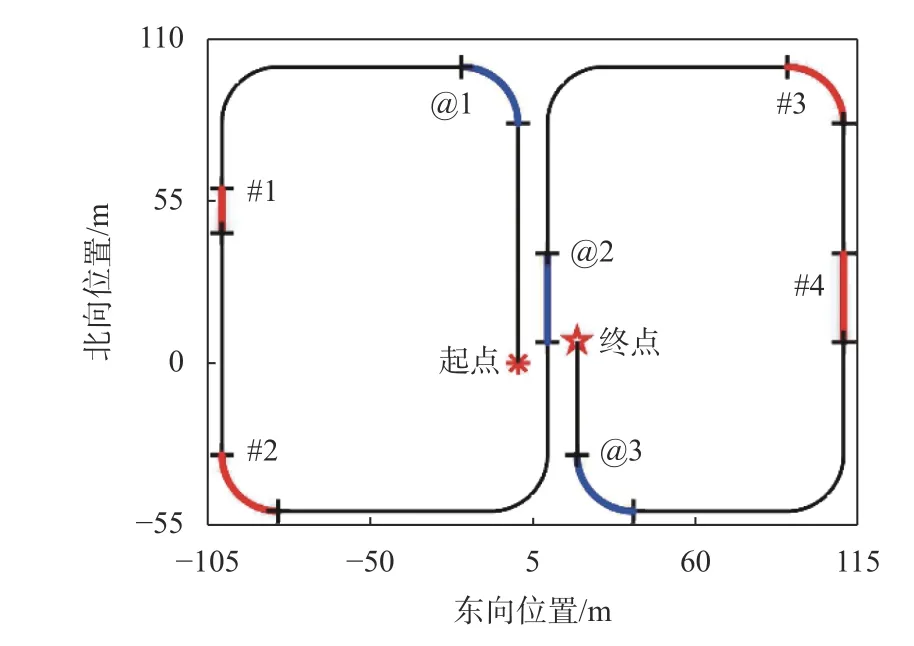
圖4 運動軌跡路線圖

為了模擬GPS 信號失效的情況，在實驗中人為設定4 個衛星信號“失效”區域，在圖4 中#1、#2、#3、#4 號紅色線標記的位置，設置的衛星信號“失效”時間及載體運動狀態信息如表1 所示.這些數據作為GPS 信號失效的系統測試集，用來檢驗本文所提算法對組合定位誤差抑制的效果.

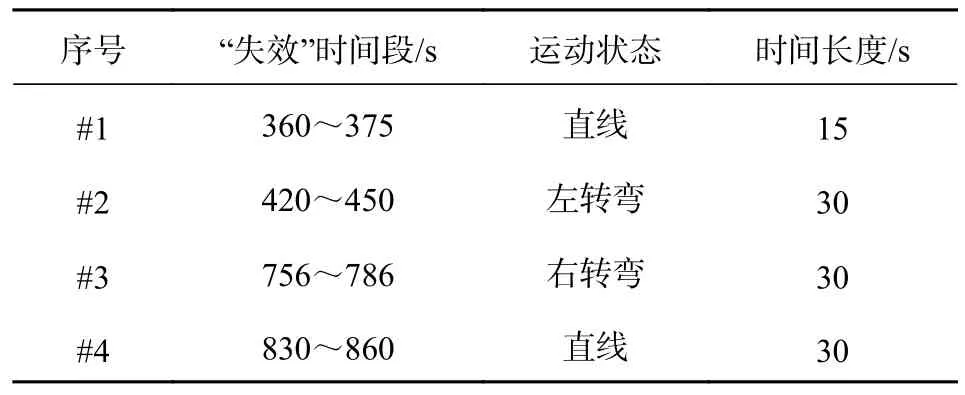
表1 GPS 信號“失效”

在GPS 信號有效區域，將IMU、SINS 和GPS 數據劃分為兩個獨立的部分：訓練集和驗證集.其中，驗證集在圖4 中@1、@2、@3 號藍色線標記的位置，設置的時間及載體運動狀態信息如表2 所示，用來確定模型的結構和超參數.其余時間部分的數據，圖4中黑色線標記的位置，作為訓練集，用來訓練優化LSTM 神經網絡模型中的參數.

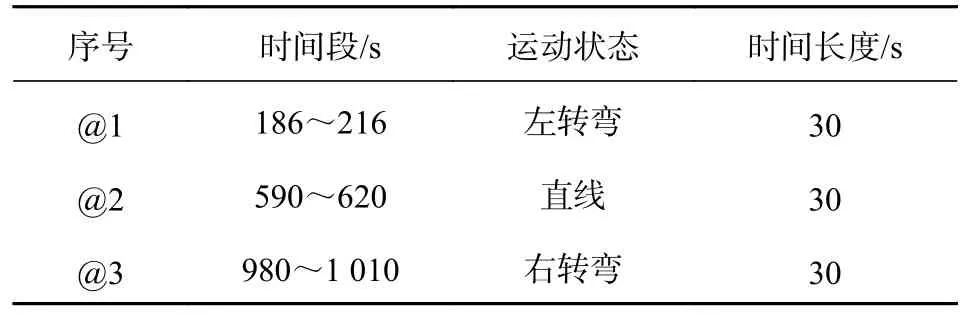
表2 驗證集

LSTM 神經網絡模型輸入層x、隱藏層L和輸出層y組成結構如圖5 所示：

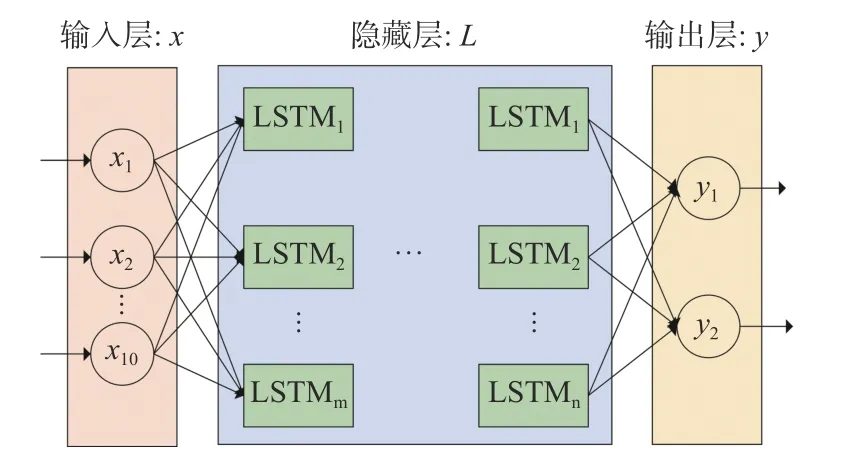
圖5 LSTM 神經網絡模型結構

其中輸入層x，包含三維加速度計輸出、三維陀螺儀輸出、SINS 輸出航向角和三維速度，共10 個輸入量；隱藏層L，不同的神經元數量和神經元間的排列結構使模型有不同擬合能力，把每層神經元數[8,16,32,64,128]和不同隱藏層數[1,2,4]自由組合，進行訓練得到的模型在驗證集上進行評估，最后得到最優的網絡包含2 個隱藏層，每層16 個LSTM 神經元；y為輸出層，包含東向位置增量和北向位置增量，共2 個輸出量.

在訓練過程中，隨著遍歷數據集的訓練輪數(epochs)的增大而造成位置增量均方根誤差(RMSE)損失的變化，如圖6 所示.

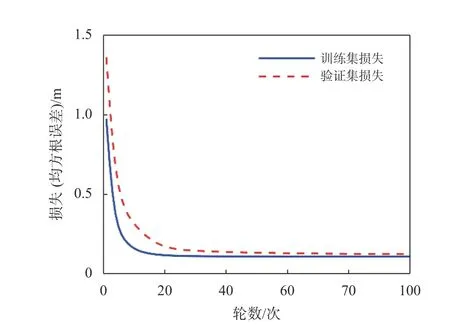
圖6 學習曲線

可以看出，訓練集和驗證集的損失將在訓練迭代50 次后降低到最小值.然后，訓練集和驗證集的損失趨于平穩，這意味著可在此時提前終止訓練，這樣即可以節省訓練時間而又不會損失任何性能.

將訓練好的模型用于系統，實驗結果通過三種方法對比實驗來分析：1)假設GPS 信號一直未“失效”，使用SINS/GPS 組合定位；2)在GPS 信號有效區域，使用SINS/GPS組合定位.在選中的4 個GPS 信號“消失”區域，不做任何處理，SINS使用IMU 輸出的數據直接解算；3)在GPS 信號有效區域，使用SINS/GPS組合定位.在選中的4 個GPS 信號“消失”區域，使用已經訓練好的LSTM神經網絡模型進行預測，然后積分，作為偽GPS位置信息.使用偽GPS 的位置和SINS 解算位置的差作為觀測信息進行數據融合.三種方法解算出的東向位置、北向位置誤差對比如圖7、圖8 所示，東向速度、北向速度誤差對比如圖9、圖10 所示.

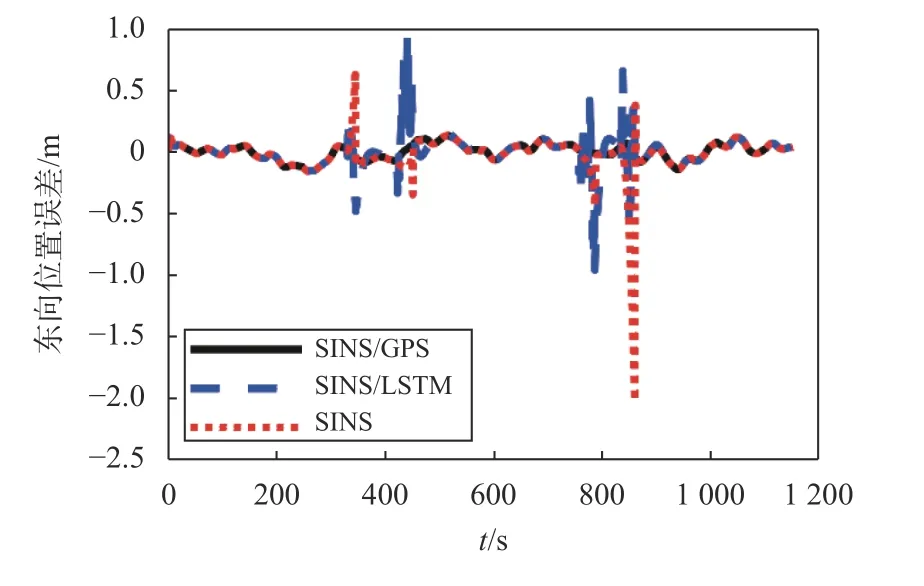
圖7 東向位置誤差

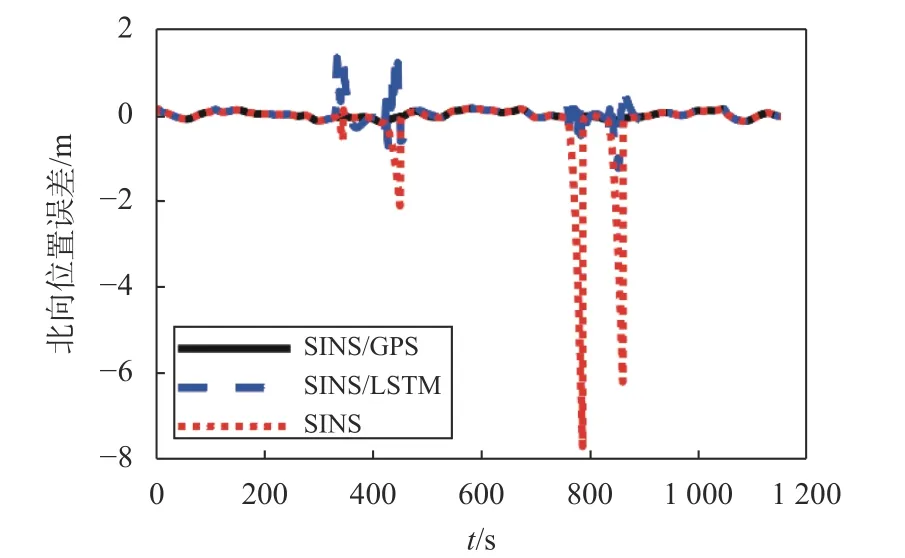
圖8 北向位置誤差

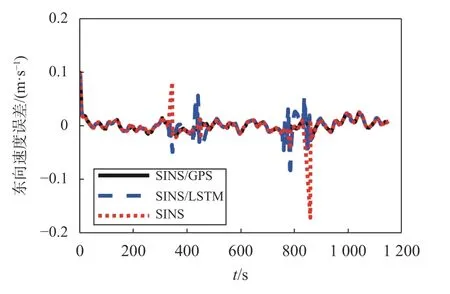
圖9 東向速度誤差

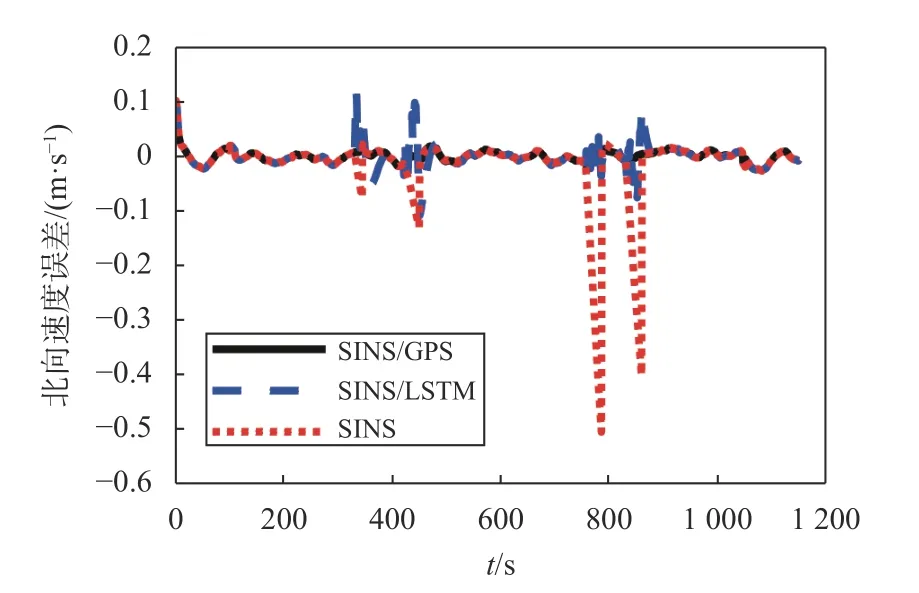
圖10 北向速度誤差

通過東北方向位置和速度誤差結果可以看出，在GPS 信號有效區域，組合定位系統經過對準后，其東向位置和北向位置誤差小于0.2 m，東向速度和北向速度誤差小于0.01 m/s，證明KF 用于組合定位的有效性；在GPS 信號失效區域，使用單獨SINS 解算，位置誤差和速度誤差將快速發散.引入LSTM 神經網絡輔助后，位置誤差和速度誤差發散得到了有效抑制.在設置的4 個GPS 信號“失效”區域，不同方案的位置RMSE 如表3 所示，速度RMSE 如表4所示.

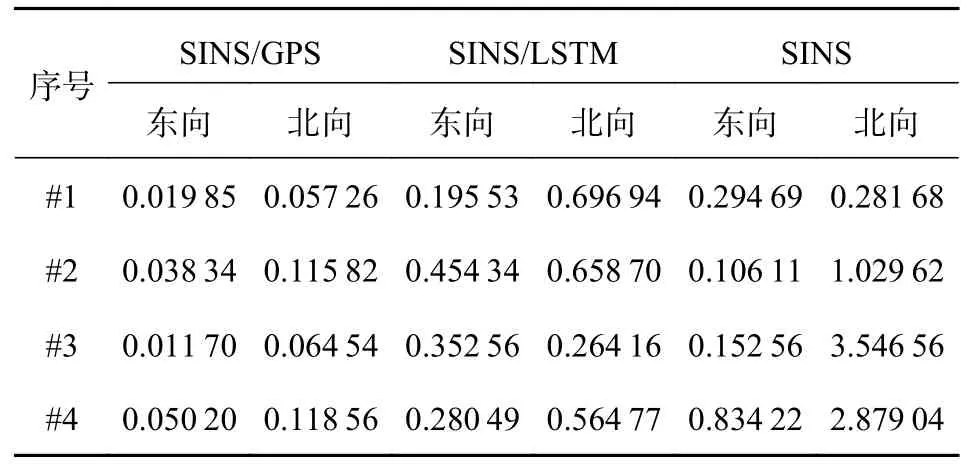
表3 不同位置RMSEm

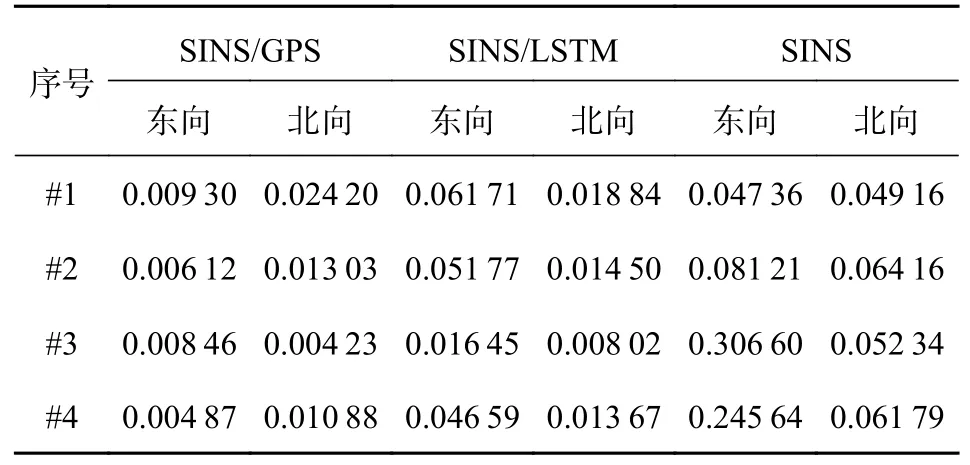
表4 速度RMSEm/s

結合表3、表4 可以看出，在#1 號區域，GPS 信號“失效”15 s的直線運動，LSTM 神經網絡輔助系統的位置誤差和速度誤差相比較純SINS 的位置誤差和速度誤差相比有較大的改善.對比#4 號區域，GPS 信號“失效”30 s的直線運動，位置和速度誤差均增大，但相比純SINS 的指數級發散，LSTM 神經網絡輔助系統的定位結果依然在可控制范圍，短時間內可以滿足定位精度要求.相比#2 號區域，GPS 信號“失效”30 s的左轉彎運動，和#3 號區域，GPS 信號“失效”30 s的右轉彎運動.LSTM 神經網絡輔助系統對東向位置輔助作用有所減弱，但在北向位置和東北方向的速度依然能保持較平穩的誤差增長.

仿真實驗充分證明了本文提出的LSTM 神經網絡輔助算法，在地籍測量中GPS 信號失效區域能夠有效防止系統進入純SINS 解算模式，維持系統定位精度.并且載體在直線、轉彎等不同的運動狀態下，依然能保持較高的精度，具有良好的魯棒性.

5 結束語

本文根據地籍測量過程GPS 信號頻繁失效和可事后離線處理的特點，提出了一種LSTM 神經網絡輔助的SINS/GPS 組合定位誤差抑制算法.根據對SINS/GPS 組合定位輸入、輸出信號特點分析，確定OSINS～δPGPS神經網絡模型結構.利用GPS有效區域的SINS/GPS 組合系統輸入、輸出信號，優化LSTM神經網絡參數.在GPS 信號失效區域，根據已經訓練好的神經網絡預測GPS 位置增量信息，對位置增量積分得到偽位置信息，然后對組合定位KF 進行量測更新，防止KF 得不到更新而進入純SINS 模式，從而抑制組合定位的誤差發散，提升GPS 信號消失區域定位精度.由仿真結果可得，采用LSTM 預測輔助KF 的組合定位方法，對于載體定位誤差有著較為明顯的抑制效果.對基于INS 和GPS 的組合定位系統在地籍測量中的應用有著一定參考價值.在測量過程中可不斷收集有效數據，從海量的數據中提升模型的表現能力.因此，本文所研究的方法具有一定的實際意義.