可信測度空間下的似乘算子模糊概率積分研究

趙 輝，姜欣格，單云霄

(哈爾濱理工大學 理學院,哈爾濱 150080)

0 引 言

1974年，日本學者Sugeno首先提出了模糊測度與積分的概念。模糊測度作為一個全新的理論得到了快速的發展。模糊積分作為由傳統積分演化而來的一種積分，具有兩種形式一種是具有可加性的模糊積分；另一種是不具有可加性的模糊積分，后者是現在研究的主要內容。

1984年王震源[1]定義了集函數的“自連續”與“零可加”。2002年HABIL E等[2]研究了經典概率論在模糊概率論中是否具有有效性的問題，由此提出了模糊概率的概念，并將一般變量演變為模糊隨機變量，在模糊概率條件下證明了中心極限定理。2003年[3]EN-LIN Lü等利用區間概率對模糊事件的隨機變量進行了研究，最終得到了模糊概率定理，與此同時還對其數學期望和方差的相關內容進行了研究。2005年MESIAR R[4]首先對一般的模糊積分及性質進行了研究，又對正則模糊積分進行了研究，最后將模糊測度與積分進行了總結。2006年成和平[5]對模糊值函數的Sugeno積分進行了研究，得到了當函數a.e.相等時，兩個函數積分極限相等；函數積分、極限均相等時，兩個函數積分極限相等。

2010年曹興陽[6]先從經典測度的角度研究了隨機變量的收斂性，又運用概率論語言對概率進行了研究，并對其收斂性進行分析。同年，李艷紅等[7]在廣義Sugeno條件下，對一種非負可積函數積分的確界形式進行研究，又得到了一些運算性質。MERIGO J M等[8]在模糊概率中加入加權平均算子來進行廣泛的聚合運算。

模糊積分在模糊數學中占有重要的地位，其中非可加的模糊積分受到學者們的廣泛關注[9-15]，2012年Liu Y[16]等在直覺模糊值Sugeno積分的基礎上研究了區間模糊值Sugeno積分。2015年HALAR等[17]對離散SUGENO積分進行分析得到了一些新的性質。SMREK P[18]在2015年對幾種Sugeno積分進行了對比分析。2016年TAJNER-PAPUGA I[19]以模糊測度為背景建立積分，得到了Sugeno積分特定模糊量的均值。2017年時婧婧[20]構造了模糊貝葉斯概率評估模型，用來解決網絡信息安全問題，得到了較好的效果。

本文主要通過t-模和s-模定義條件設計了一個似乘算子和似和算子，重點對似乘算子進行了研究，在可信測度空間上結合似乘算子，重新定義了廣義Sugeno模糊概率積分，根據演化的Sugeno模糊概率積分定義獲得了此積分的一般性質及弱絕對連續性，并給出了可測函數a.e.相等時，測度是零可加的等一些定理的證明。

1 預備知識

定義1設X為非空集合，由X的一些子集構成的σ-代數即為F，集函數μ：F→[0，∞]是F上的模糊測度，若滿足：

1)μ(?)=0；

2)A∈F，B∈F，A?B?μ(A)≤μ(B)；

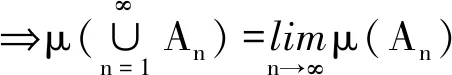
且?n0使

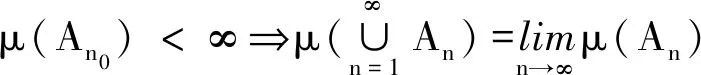
當μ滿足1)，2)，3)，μ稱為下半連續模糊測度；當μ滿足1)，2)，4)，μ稱為上半連續模糊測度。

若μ是可測空間(X，F)上的模糊測度，則(X,F,μ)稱為模糊測度空間。

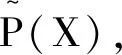
1)μ(?)=0，μ(X)=1；

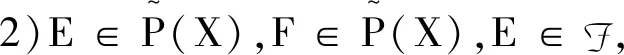
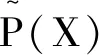
定理1概率空間為(X,A,P)，概率測度P：A→[0,1]滿足以下條件：

1)P(X)=1；

2)?i≠j，Ai∩Aj=?，

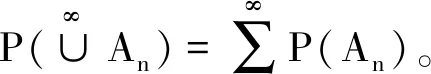
如果{An}滿足A1?A2?…?An?…，則稱{An}為單調增序列，記為“An”；

如果{An}滿足A1?A2?…?An?…，則稱{An}為單調減序列，記為“An”。

定義3設f是模糊測度空間(X,F,μ)→[0,∞]的可測函數，記

Nα(f)={x|f(x)>α} (α∈[0,∞))

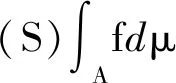
定義4映射Τ：[0,1]×[0,1]→[0,1]，若?a,b,c,d∈[0,1]滿足：

1)交換律：Τ(a,b)=Τ(b,a)；

2)結合律：Τ(Τ(a,b),c)=Τ(a,Τ(b,c))；

3)單調性：

a≤c，b≤d?Τ(a,b)≤Τ(c,d)；

4)邊界條件：Τ(1,a)=a

則稱Τ為[0,1]上的t-模算子。

2 主要結果

定義4設映射T:[0,1]×[0,1]→[0,1]，?a,b∈(0,1]，構造似乘算子：

1)交換律：T(a，b)=T(b，a)；

2)單調性：若a≤c,b≤d，則

T(a,b)≤T(c,d)；

3)結合律：

T(T(a，b)，c)=T(a，T(b，c))；

4)邊界條件：T(1，a)=a。

證明:

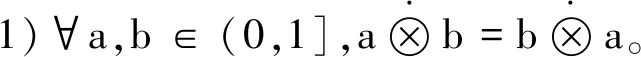
2)?a,b,c,d∈(0,1],a≤c,b≤d?ab≤cd,a+b≤c+d則

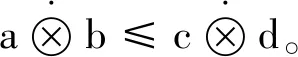
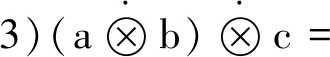
定義5設映射⊥:[0,1]×[0,1]→[0,1]，?a,b∈[0,1]，構造似和算子：

1)交換律：⊥(a，b)=⊥(b，a)；

2)單調性：若a≤c,b≤d，則

⊥(a,b)≤⊥(c,d)；

3)結合律：

⊥(⊥(a，b)，c)=⊥(a，⊥(b，c))；

4)邊界條件：⊥(a，0)=a。

證明:

2)?a,b,c,d∈[0,1],a≤c,b≤d?ab≤cd,a+b≤c+d則

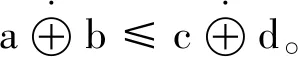
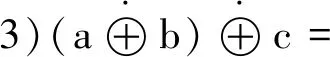
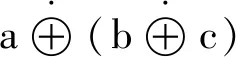
下面給出一種特殊的模糊測度——可信測度：

定義6設μ:F→[0,1]稱為(X,F)上的一個可信測度，F表示一個σ-代數。當且僅當：

1)?處為零：當?∈F時，μ(?)=0；

2)μ(X)=1；

3)單調非減性：?A,B∈F,A?B?μ(A)≤μ(B)；

4)可信性：若μ為(X,F)上的集函數，μ′為(X,F′)上的集函數，F?F′且?A∈F，則有μ(A)=μ′(A)；

則稱為可信測度，可信測度是概率測度的一種特殊形式，(X,F,μ)稱為可信測度空間。當且僅當?A,B∈F，μ(B)=0且A∩B=?，取Bn=B(n=1,2,…)，有limμ(Bn)=μ(B)=0稱可信測度μ是零可加的，即μ(A∪B)=limμ(A∪Bn)=μ(A)。

定理4設μ是F上的可信測度，μ′是F′上的可信測度，A,Ac∈F，μ(A)+μ(Ac)=1，則μ滿足下連續性。

證明：由題意可知，對?{An}?F，F?F′，A1?A2?…?An?…， 有

A1c?A2c?…?Anc?…，且

故有

因此μ是下連續的。

下面對可信測度空間下的廣義Sugeno模糊概率積分進行研究：

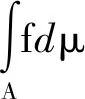
Nα(f)={x|f(x)≥α,x∈X}(α∈[0，1])

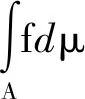
1)若f1≤f2，則

2)對?c∈[0，1]，

3)若A?B，則

證明:1)因為f1≤f2，根據定理2和定義7可知，有

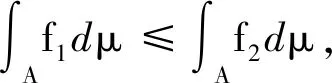
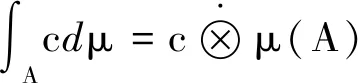
3)因為A?B，?α∈[0,1]，(A∩Nα(f))?(B∩Nα(f))

又因為μ具有單調性，所以

μ(A∩Nα(f))≥μ(B∩Nα(f))故

4)A∈F，f1，f2為可測函數，

5)A∈F，f1，f2為可測函數，

綜上所述，結論成立。

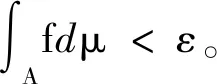
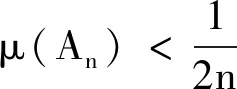
但由定義2.2知

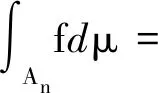
μ(An)

因此

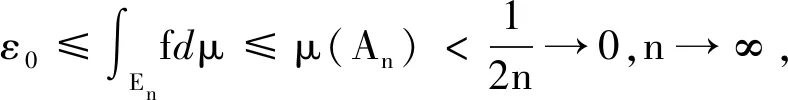
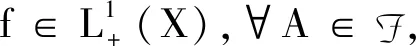
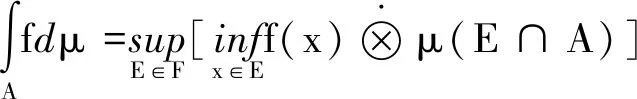
證明:?α∈[0,1]，x∈Nα(f)，f(x)≥α左右同取下確界：

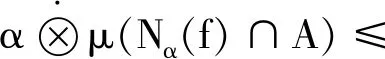
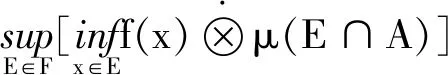
式子左右同取上確界，且式子右邊與α無關，?α∈[0,1]，從而

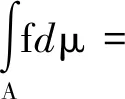
又有?E∈F，對式子兩端同時取下確界：

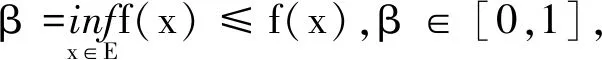
再對式子左右同取上確界，等式右邊與E無關，所以

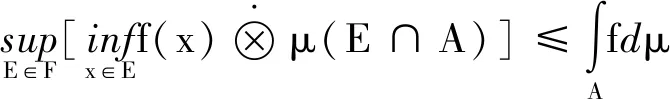
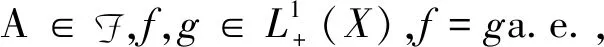
證明：

充分性：因為f=g，a.e.，設B={x∈X;f(x)≠g(x)}，則μ(B)=0，?α∈[0,1]，x0∈Nα(f)，即f(x0)≥α。

當f(x0)=g(x0)時，x0∈Nα(g)；

當f(x0)≠g(x0)時，x0∈B，因此Nα(f)?Nα(g)∪B。

因為μ具有單調性和零可加性，則有

μ(Nα(f))≤μ(Nα(g)∪B)=μ(Nα(g))

則

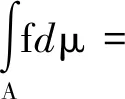
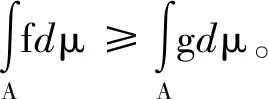
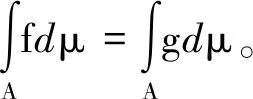
必要性(反證法)：若μ不具有零可加性，則有?A∈F，B∈F，μ(B)=0，但μ(A∪B)≠μ(A)?μ(A∪B)>μ(A)。

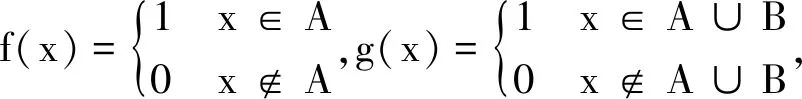
{x∈X;f(x)≠g(x)}=

(A-A∪B)∪(A∪B-A)=

(A∩(Ac∩Bc))∪((A∩Ac)(B∩Ac))=

B∩Ac?B

因此

0≤μ({x∈X;f(x)≠g(x)})≤μ(B)=0?f=g有

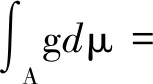
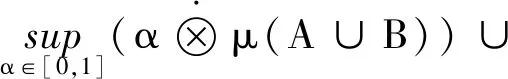
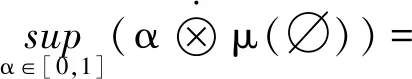
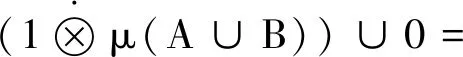
μ(A∪B)

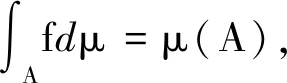
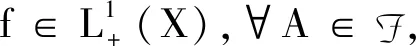
證明：設

B={x∈A;f(x)≠0}={x∈A;f(x)>0}，C={x∈A;f(x)≠0}，

則A=B∪C，A∩B=?，μ(B)=0，?α∈(0,1]，有

0≤μ(Nα(f)∩B)≤μ(B)=0，

Nα(f)∩C={x∈A;α≤0}=?

因此

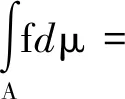
=0

綜上所述，結論成立。

3 結 論

本文構造了一個模糊似乘算子和似和算子，證明該算子滿足t-模和s-模條件，又建立了一個新的測度空間—可信測度，主要研究了在可信測度空間下將模糊似乘算子與Sugeno模糊概率積分相結合得到的新積分形式并證明相關的定理和性質均成立。對于模糊似和算子的部分將在后續研究中作為重點內容進行深入研究。