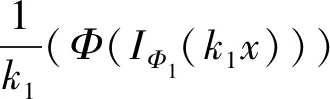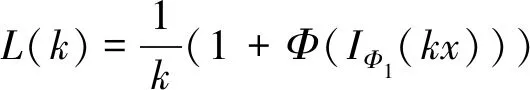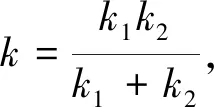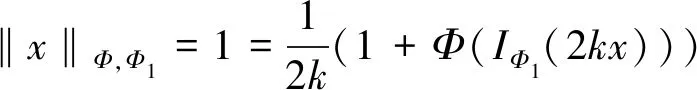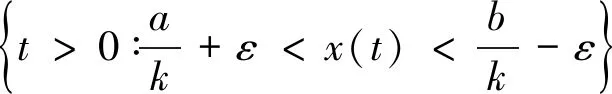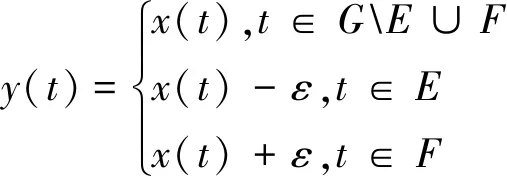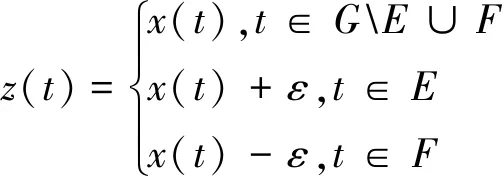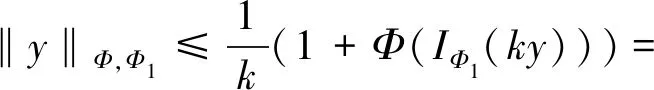賦Φ-Amemiya范數(shù)的Orlicz空間的端點

崔云安，安莉麗

(哈爾濱理工大學(xué) 理學(xué)院，哈爾濱 150080)

0 引 言

Orlicz空間作為一類特殊的Banach空間，自從1932年波蘭數(shù)學(xué)家Orlicz引入Orlicz空間以來，Orlicz空間理論就因其重要的理論和應(yīng)用價值受到了許多數(shù)學(xué)工作者的關(guān)注，并在微分方程、逼近論、控制論、不動點等許多數(shù)學(xué)分支學(xué)科中得到了廣泛應(yīng)用[1]。在其發(fā)展過程中主要出現(xiàn)了3個范數(shù)：1932年由Orlicz本人給出了Orlicz范數(shù)的定義[2]；1955年，Luxemburg在Orlicz空間中引入了Luxemburg范數(shù)[3]；2008年崔云安和段麗芬引入了p-Amemiya范數(shù)[4-7]。眾所周知，關(guān)于賦Orlicz范數(shù)、Luxemburg范數(shù)以及p-Amemiya范數(shù)的Orlicz空間性質(zhì)的研究已經(jīng)比較成熟，所以對Orlicz空間的新性質(zhì)的進(jìn)一步研究是十分重要的[8-9]。我們將研究比上述3種范數(shù)更具有廣泛意義的新范數(shù)，賦Φ-Amemiya范數(shù)的Orlicz空間的可達(dá)性、端點和嚴(yán)格凸性。主要給出了范數(shù)可達(dá)的充要條件和端點的判別準(zhǔn)則，并據(jù)此得到了賦Φ-Amemiya范數(shù)的Orlicz空間嚴(yán)格凸的充要條件。

1 預(yù)備知識

本文以X表示一個Banach空間，B(X)和S(X)分別表示閉單位球和單位球面。

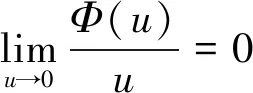
設(shè)L0表示定義在G上的可測實函數(shù)全體，

定義IΦ：L0→R+=[0,+∞)如下：

由Orlicz函數(shù)生成的Orlicz空間記為

LΦ={x∈L0:?λ>0,IΦ(λx)<∞}

關(guān)于Orlicz范數(shù)(Amemiya范數(shù))：

Luxemburg范數(shù)：

以及廣義Orlicz范數(shù)：

均成為Banach空間[11-15]，簡記為:

LΦ=[LΦ,‖·‖ΦΦ]

LΦ,p=[LΦ,‖·‖ΦΦ,p]

定義2設(shè)Φ1是N-函數(shù)，(G,∑,μ)是無原子有限測度空間，記L0(G)為G上的μ-可測函數(shù)的全體。定義模IΦ,Φ1∶L0(G)→R如下：

由Φ1及Φ是凸函數(shù)知，IΦ,Φ1為凸模，記

LΦ,Φ1={x∈L0(G)∶?λ>0,IΦ,Φ1(λx)<+∞}

定義3設(shè)Φ是Orlicz函數(shù)，滿足max{0,u-1}≤Φ(u)，在LΦ,Φ1(或EΦ,Φ1)上賦Amemiya范數(shù)，稱為Φ-Amemiya范數(shù):

利用Φ-Amemiya與Luxemburg范數(shù)等價，很容易得{LΦ,Φ1,‖·‖ΦΦ,Φ1}是Banach空間。

定義4x∈S(X)稱為端點是指

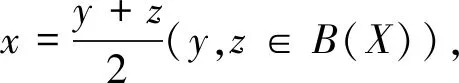
定義5稱N-函數(shù)滿足Δ2條件是指存在k>2，u0≥0滿足：

Φ(2u)≤kΦ(u) (u≥u0)

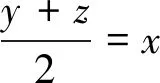
2 主要結(jié)果及證明

先引入兩個記號:

|x(t)|dt-Φ(IΦ1(kx))≥1}

|x(t)|dt-Φ(IΦ1(kx))≤1}

定理1當(dāng)且僅當(dāng)k∈[k*,k**]時，

D(x)={0

取x∈LΦ,Φ1{0}，D0(x)為D(x)的內(nèi)點集對?0

所以對?k∈D0(x)函數(shù)

按通常數(shù)學(xué)分析規(guī)則可求得：

Φ(IΦ1(kx))-1}

假設(shè)?k0∈D0(x)使得k*≤k0≤k**，則對0

Φ(IΦ1(kx))≤1,對k∈D0(x)∩(k0,∞)

Φ(IΦ1(kx))≥1。

所以對

對k∈D0(x)∩(k0,∞),

因此當(dāng)且僅當(dāng)k*≤k0≤k**時

推論1若Φ1是N-函數(shù)，則

k(x)≠?(x≠0)。

則L(k)是關(guān)于k的連續(xù)函數(shù)。

由Φ1是N-函數(shù)可得

故k(x)≠?。

定理2若Φ1是N-函數(shù)，x∈S(LΦ,Φ1)是B(LΦ,Φ1)端點的充分必要條件是:

μ({t∈G,kx(t)∈RSΦ1})=0，k∈K(x)

2=‖y‖Φ,Φ1+‖z‖Φ,Φ1=

2‖x‖Φ,Φ1=2

即2k∈K(x)。

并且對幾乎所有的t∈G都有

Φ1(2kx(t))

再由已知條件2kx(t)∈SΦ1可得，對幾乎所有的t都有k1y=k2z，所以

k1=‖k1y‖Φ,Φ1=‖k2z‖Φ,Φ1=k2。

因此y=z這就說明x為B(LΦ,Φ1)的端點。

必要性(反證法)假設(shè)結(jié)論不成立。不失一般性，設(shè)k∈K(x)，μ({t∈G∶kx(t)∈RSΦ1})>0， 因為SΦ1的余集可表示為至多可列個開區(qū)間的并集,所以必存在某個開區(qū)間(a,b)，使得Φ(x)在(a,b)上是線性的，Φ(x)=px+q。并且存在ε>0，使得

將集合

由μ(E)=μ(F)>0，可知y≠z。

當(dāng)t∈GE∪F時，ky(t)=kx(t)∈(a,b)。

當(dāng)t∈E時，ky(t)=k(x(t)-ε)

又a

所以ky(t)∈(a,b)

當(dāng)t∈F時，ky(t)=k(x(t)+ε)

又a+2kε

所以ky(t)∈(a,b) 于是

由此可得:IΦ1(ky)=IΦ1(kx)

同理可得‖z‖Φ,Φ1≤1

這與x為B(LΦ,Φ1)的端點矛盾。

定理3若Φ1是N-函數(shù)，LΦ,Φ1是嚴(yán)格凸的充要條件是Φ1是嚴(yán)格凸的。

證明：充分性由定理2立即可得。接下來證必要性。

若Φ1非嚴(yán)格凸，則存在x0?SΦ1取E1?G，使得0<μE1<μG，且Φ1(x0)μE1≤1，Ψ1(p(x0))μE1≤1。

再取x1>0，使得

Φ1(x1)μ(GE1)≥1和Ψ1(p(x1))μ(GE1)≥1，

于是

Φ1(x0)μ(E1)+Φ1(x1)μ(GE1)≥1

Ψ1(p(x0))μ(E1)+Ψ1(p(x1))μ(GE1)≥1

即

Φ1(x0)μ(E1)+Φ1(x1)μ(GE1)+

Ψ1(p(x0))μ(E1)+Ψ1(p(x1))μ(GE1)≥2

對于Orlicz函數(shù)Φ取

Φ′(Φ1(x0)μ(E1)+Φ1(x1)μ(GE1))·

(Φ1(x0)μ(E1)+Φ1(x1)μ(GE1)+

Ψ1(p(x0))μ(E1)+Ψ1(p(x1))μ(GE1))-

Φ(Φ1(x0)μ(E1)+Φ1(x1)μ(GE1))≥1

然后選E2?GE1,滿足

Φ′(Φ1(x0)μ(E1)+Φ1(x1)μE2)·

(Φ1(x0)μ(E1)+Φ1(x1)μE2+

Ψ1(p(x0))μ(E1)Ψ1(p(x1))μE2)-

Φ(Φ1(x0)μ(E1)+Φ1(x1)μE2)=1

令

k=1+Φ(Φ1(x0)μ(E1)+Φ1(x1)μE2)

則

Φ′(Φ1(x0)μ(E1)+Φ1(x1)μE2)·

(Φ1(x0)μ(E1)+Φ1(x1)μE2+

Ψ1(p(x0))μ(E1)+Ψ1(p(x1))μE2)-

Φ(Φ1(x0)μ(E1)+Φ1(x1)μE2)=1

但μ(t∈G∶kx(t)?SΦ1)≥μE1>0。

由定理2得，x不是B(LΦ,Φ1)的端點，產(chǎn)生矛盾。