b-凸度量空間的不動點理論
李朝博,陳麗麗
(哈爾濱理工大學 應用數學系, 黑龍江 哈爾濱 150080)
0 引 言
不動點理論在非線性泛函分析中扮演著非常重要的角色,在應用數學和其他領域都有著廣泛的應用。不動點理論有著悠久的歷史,1910年,荷蘭數學家Brouwer創立了布勞威爾不動點定理,由此開啟了不動點理論研究的先河[1]。1922年,波蘭數學家Banach提出了著名的壓縮映象原理,其結果的優美性和證明的簡潔性,吸引了大批學者的關注,被廣泛應用在數學領域并成功解決了許多數學問題,諸如隱函數存在定理,微分方程解的存在唯一性等一系列重大問題,使得不動點理論引起了國內外數學界的高度重視和深入研究[2]。隨著不動點理論的不斷發展完善,一系列新穎的壓縮映射、非擴張型映射以及相應的不動點定理相繼問世,并成功應用于微分方程、拓撲、經濟均衡、對策論和優化控制等諸多領域,不動點理論已成為現代數學的重要分支。許多國內外學者利用Banach空間的幾何性質對對各種非擴張型單值映射和非擴型集值映射的不動點性質進行了深入研究,所取得的研究成果極大地豐富和發展了不動點理論。隨著不動點理論的不斷發展,人們已經不滿足于現狀,通過各種方式對度量空間進行推廣。1993年,Czerwik提出了b-度量空間的概念,并在該空間中給出了壓縮映射的不動點定理[3]。隨后,國內外眾多學者對b-度量空間的不動點理論進行了廣泛的研究,例如,1994年,Matthews提出了偏序度量空間的概念[4];2013年,Shukla在b-度量空間與偏序度量空間的基礎上提出了偏序b-度量空間的概念[5];2011年,Hussian和Shah提出了錐b-度量空間[6]。更多關于b-度量空間的研究成果見文[7-14]。
1970年,Takahashi提出了凸結構的概念,并給出了凸度量空間在非擴張映像下的不動點理論[15-16]。隨后,Kink與Goebal研究了凸度量空間的迭代問題[17]。更多關于凸結構的研究見文獻[18-22]。本文在此基礎上,繼續對b-度量空間進行研究推廣,在b-度量空間中引入了凸結構,從而給出b-凸度量空間的概念,并在該空間中給出了Mann迭代算法。進一步利用Mann迭代生成序列,證明了完備的b-凸度量空間的不動點性質。
1 預備知識
定義1[23]設X是一個非空集合,令d∶X×X→[0,+∞),若對任意x,y,u∈X滿足:
1)d(x,y)=0,當且僅當x=y;
2)d(x,y)=d(y,x);
3)d(x,y)≤s[d(x,u)+d(u,y)]。
其中s≥1。則稱d是X上的一個b-度量,稱(X,d)為b-度量空間,s為其系數。很顯然,s=1時,d就是通常意義的度量。
定義2[24]設(X,d)為度量空間,連續映射w∶X×X×[0,1]→X,若對于所有x,y,u∈X,α∈[0,1],有以下不等式成立:d(u,w(x,y,α))≤αd(u,x)+(1-α)d(u,y)則w稱作X上的一個凸結構,(X,d,w)稱為凸度量空間。
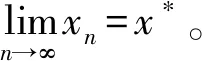
{xn}稱為X中的Cauchy列,如果?ε>0,存在自然數n0,當n,m≥n0時有d(xn,xm)<ε。(X,d)稱為完備的b-度量空間,若X中的每一個Cauchy列都收斂。
2 主要結果
定義4設(X,d)為b-度量空間,連續映射w∶X×X×[0,1]→X,若對于任意的x,y,u∈X, 有以下不等式成立:
d(u,w(x,y,α))≤αd(u,x)+(1-α)d(u,y)則稱(X,d,w)為b-凸度量空間。
在一般的線性空間中,Mann迭代格式定義如下:
xn+1=αnxn+(1-αn)Txn
下面利用凸結構將Mann迭代格式引入到b-度量空間中,格式如下:
例1令X=R,令d(x,y)=|x-y|r,其中r為任意實數且r>1。很顯然d滿足定義1中的(1)和(2)。此外,對任意的x,y,z∈X有
d(x,y)=|x-y|r=|x-z+z-y|r≤
[|x-z|+|z-y|]r≤
2r-1[|x-z|r+|z-y|r]=
2r-1(d(x,z)+d(z,y))
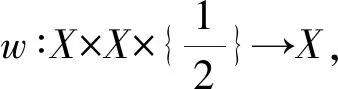
易知w為連續映射,下面驗證其滿足對任意的x,y,u∈X有
d(u,w(x,y;α))≤αd(u,x)+(1-α)d(u,y)
事實上,
d(u,w(x,y;α))=|u-[αx+(1-α)y]|r≤
2r-1[αr|u-x|r+(1-α)r|u-y|r]=
αd(u,x)+(1-α)d(u,y),
則(X,d,w)是一個s=2r-1的b-凸度量空間。此外,(X,d,w)不是一個通常意義下的度量空間,例如r=2時,
d(2,4)=4>d(2,3)+d(3,4)=2
例2令X=Rn,對任意的
x=(x1,x2,…,xn),y=(y1,y2,…,yn)∈X,
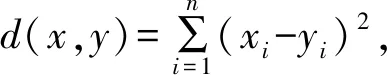
由于
2(d(x,u)+d(u,y))
易知d滿足定義1的(1)和(2),所以(X,d)為s=2的b-度量空間。設
滿足w(x,y;α)=αx+(1-α)y
易知w為連續映射,對任意的x,y,u∈X有
d(u,w(x,y;α))≤αd(u,x)+(1-α)d(u,y)
事實上,
d(u,w(x,y;α))=
αd(u,x)+(1-α)d(u,y)
所以(X,d,w)是一個s=2的b-凸度量空間。但(X,d,w)不是一個通常意義下的度量空間,例如n=1時,見例1。
注 例1和例2都是在b-凸度量空間中引入連續映射w(x,y;α)=αx+(1-α)y作為凸結構。但下面的例子說明對于同一個映射w,在某些b-度量空間中,將不能構成凸結構。
例3令X=lp,0 定義映射d∶X×X→R+∪{0},滿足 對于任意 x={xn},y={yn},u={un}∈lp, 由 2(1-p)/p(d(x,u)+d(u,y)) 易知(X,d)是系數為s=2(1-p)/p>1的b-度量空間。設連續映射w,滿足 w∶X×X×[0,1]→X, 對于任意x,y∈X,令 w(x,y;α)=αx+(1-α)y 下面取xn d(u,w(x,y;α))= αd(u,x)+(1-α)d(u,y) 此時w不是凸結構。 定理1設(X,d,w)為完備的b-凸度量空間,映射T∶X→X滿足下列不等式 d(Tx,Ty)≤βd(x,y),?x,y∈X 設連續映射w∶X×X×[0,1]→X,令 xn+1=w(xn,Txn;αn),d(x0,Tx0)=M<∞, 證明: d(xn,xn+1)=d(xn,w(xn,Txn;αn))≤ (1-αn)d(xn,Txn) d(xn,Txn)≤sd(xn,Txn-1)+sd(Txn-1,Txn)≤ sd(w(xn-1,Txn-1;αn-1),Txn-1)+sβd(xn-1,xn)≤ s[αn-1d(xn-1,Txn-1)+β(1-αn-1)d(xn-1,Txn-1)]= s[αn-1+β(1-αn-1)]d(xn-1,Txn-1) 令λn-1=s[αn-1+β(1-αn-1)], 因為 從而得到λ<1。則 d(xn,Txn)≤λ(xn-1,Txn-1) d(xn-1,Txn-1)≤λ(xn-2,Txn-2) … d(x1,Tx1)≤λ(x0,Tx0) 因此 d(xn,Txn)≤λn(x0,Tx0) d(xn,xn+1)≤(1-αn)λnd(x0,Tx0)≤ λnd(x0,Tx0) d(xn,xn+p)≤sd(xn,xn+1)+sd(xn+1,xn+p)≤ sd(xn,xn+1)+s2d(xn+1,xn+2)+s2d(xn+2,xn+p)≤…≤ sd(xn,xn+1)+s2d(xn+1,xn+2)+…+ sp-1d(xn+p-1,xn+p)+sp-1d(xn+p-1,xn+p)≤ (sλn+s2λn+1+…+sp-1λn+p-1)d(x0,Tx0)≤ λn(s+s2+…+sp-1)d(x0,Tx0) 當n→∞時,顯然λn→0,所以對任意自然數P,d(xn,xn+p)→0,從而可知{xn}為Cauchy列。 由空間的完備性知,存在x*∈X,使得xn→x*∈X,(n→∞)。注意到 d(x*,Tx*)≤s[d(x*,xn)+d(xn,Tx*)]≤ sd(x*,xn)+s2[d(xn,Txn)+d(Txn,Tx*)]≤ sd(x*,xn)+s2d(xn,Txn)+s2βd(xn,x*)≤ (s+s2β)d(x*,xn)+s2d(xn,Txn)≤ (s+s2β)d(x*,xn)+s2λnd(x0,Tx0) 令n→∞, 從而d(x*,Tx*)=0,所以Tx*=x*,則T在X中存在不動點。 最后證明不動點的唯一性。假設T在X中不動點不唯一。即存在y*∈X,使得x*≠y*滿足Ty*=y*,則 d(x*,y*)=d(Tx*,Ty*)≤βd(x*,y*) 若d(x*,y*)≠0,由于 0<β<1,產生矛盾,故d(x*,y*)=0,即x*=y*。所以T在X中存在唯一的不動點。 d(x,y)=(x-y)2 設連續映射w∶X×X×[0,1]→X,滿足 w(x,y;α)=αx+(1-α)y 令xn+1=w(xn,Txn;αn), 證明:由例1易知(X,d)為s=2的b-度量空間,又因為,對任意x,y,u∈X,有 d(u,w(x,y;α))=d(u,αx+(1-α)y)= [α(u-x)+(1-α)(u-y)]2≤ [α|u-x|+(1-α)|u-y|]2= (α|u-x|)2+((1-α)|u-y|)2+2α(1- α)|u-x||u-y|≤ (α|u-x|)2+((1-α)|u-y|)2+α(1- α)(|u-x|2+|u-y|2)= α(u-x)2+(1-α)(u-y)2= αd(u,x)+(1-α)d(u,y) 即(X,d,W)為s=2的b-凸度量空間。 以此計算 … 從而得到第n項, xn=αn-1xn-1+(1-αn-1)Txn-1= 易知n→∞,xn→0∈X,Txn→0∈X,所以0是T在X中的不動點。假設存在兩個不動點x*,y*∈X,x*≠y*滿足Tx*=x*,Ty*=y*,則 所以d(x*,y*)=0,即x*=y*,所以0是T在X中唯一的不動點。 注 在度量空間中,通過引入凸結構,使得度量空間兼具了線性結構的優點,便可以構造Mann迭代序列,克服了簡單迭代法的一些缺陷,并去掉了加在非線性算子上的一些限制條件,具有較大的優越性。接下來,我們給出膨脹映射下Mann迭代序列收斂到唯一不動點的例子。 例5令X=R+∪{0},對?x∈X,令Tx=2x。定義d∶X×X→X,滿足 d(x,y)=(x-y)2, 設映射w∶X×X×[0,1]→X滿足 w(x,y;α)=αx+(1-α)y, … 則有n→∞,xn→0∈X,T-1xn→0∈X,故0是T-1在X中的不動點,即T-1(0)=0。從而得到T(0)=0,所以0是T在X中的不動點。假設存在兩個不動點a≠b滿足Ta=a,Tb=b,則d(a,b)=d(Ta,Tb)=4d(a,b),產生矛盾,所以不動點是唯一的。 文章的主要工作是將凸結構引入到b-度量空間中,從而給出了新的概念b-凸度量空間,并給出b-凸度量空間的具體例子。利用凸結構首次在b-凸度量空間中給出了Mann 迭代,并利用Mann 迭代生成序列,證明了完備b-凸度量空間中壓縮映射的不動點性質。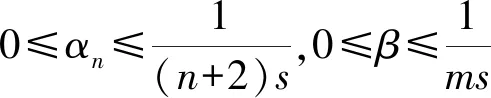
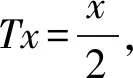
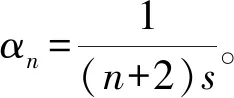
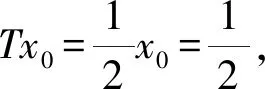
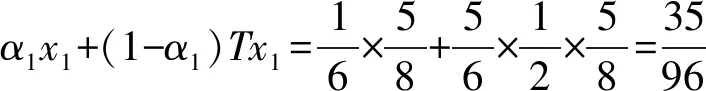
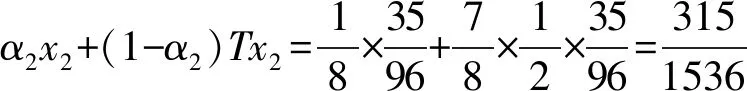
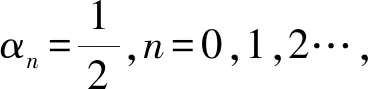
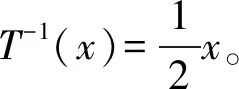
3 結 論

