核心素養(yǎng)視角下初中數(shù)學(xué)復(fù)習(xí)課教學(xué)模式的構(gòu)建

吳瑜

摘要：數(shù)學(xué)是一門邏輯性與抽象性兼?zhèn)涞膶W(xué)科，數(shù)學(xué)知識學(xué)習(xí)之后需要經(jīng)過復(fù)習(xí)鞏固，溫故而知新，才能夠得心應(yīng)手地應(yīng)用。而復(fù)習(xí)課并非簡單地進行知識羅列，科學(xué)有序的復(fù)習(xí)課對學(xué)生數(shù)學(xué)綜合素養(yǎng)的發(fā)展起著重要的作用，本文將對核心素養(yǎng)視角下初中復(fù)習(xí)課堂的構(gòu)建進行分析。

關(guān)鍵詞：核心素養(yǎng)；初中數(shù)學(xué)；復(fù)習(xí)課；教學(xué)模式

中圖分類號：G633.6文獻標(biāo)識碼：A文章編號：1992-7711（2021）28-0066

一、數(shù)學(xué)復(fù)習(xí)課教學(xué)模式建構(gòu)遵循的原則

1.整體性原則

整體性原則包含兩個方面：其一，對《課程標(biāo)準(zhǔn)》有整體的把握，將其作為教學(xué)活動的出發(fā)點和落腳點，以《標(biāo)準(zhǔn)》作為依據(jù)才能保證教學(xué)活動不偏離軌道，確保復(fù)習(xí)課堂科學(xué)有序的開展；其二，對學(xué)生學(xué)習(xí)所使用所有學(xué)習(xí)資源的整體把握，復(fù)習(xí)課將學(xué)生迄今為止所學(xué)習(xí)的數(shù)學(xué)知識進行歸攏梳理，所包含的內(nèi)容十分復(fù)雜繁多，只有對所學(xué)全部知識有著整體的把握，熟悉全部教材內(nèi)容，才能夠在繁多的知識點中牽引出一條思維散發(fā)的線條，并以此為依據(jù)形成多元素的有機知識網(wǎng)絡(luò)體系[1]。

2.主體性原則

復(fù)習(xí)課最容易出現(xiàn)的問題就是教師包辦代替一切，教師所扮演的角色是指導(dǎo)者與支持者，從簡單的知識復(fù)習(xí)到結(jié)論與方法的歸納總結(jié)，以及相關(guān)題型訓(xùn)練都應(yīng)當(dāng)由學(xué)生積極主動地參與完成，充分體現(xiàn)學(xué)生在課堂中的積極主動性，才能夠培養(yǎng)學(xué)生的數(shù)學(xué)核心素養(yǎng)，收獲最佳的數(shù)學(xué)復(fù)習(xí)效果。

3.發(fā)展性原則

發(fā)展性原則是指學(xué)生通過復(fù)習(xí)課堂能夠在自己原有基礎(chǔ)上有所收獲、有所提升與發(fā)展，使他們的思維水平與問題解答能力得到有效的鍛煉，將核心素養(yǎng)的提高作為課堂的落腳點，既充分考慮學(xué)生當(dāng)前基本水平，又重視在這一過程中他們數(shù)學(xué)解答技能、良好學(xué)習(xí)習(xí)慣的養(yǎng)成。

二、初中數(shù)學(xué)復(fù)習(xí)課的有效策略的構(gòu)建

1.多維度設(shè)置問題情境，揭露問題本質(zhì)

核心素養(yǎng)背景下，教師在組織數(shù)學(xué)復(fù)習(xí)課堂時需要遵循整體性、發(fā)展性以及主體性等多項基本原則，這也就意味著教師在為學(xué)生呈現(xiàn)問題情境時，需要考慮情境的典型性和層次性，在不同的層面、高度以及問題背景之下進行思考與解答，這能夠有效地鍛煉學(xué)生的問題思考能力，在多項訓(xùn)練中將所學(xué)習(xí)的基本知識進行熟練的變形應(yīng)用，知識遷移水平明顯提升。

例如，在組織建構(gòu)初中數(shù)學(xué)“幾何變換求線段最值問題”的復(fù)習(xí)課堂時，同一個知識點的練習(xí)，可以通過以下幾個問題情境來進行訓(xùn)練。

問題情境一：某街道要在主街道修建一個居民服務(wù)點，向街道的A社區(qū)和B社區(qū)提供便利服務(wù)，居民服務(wù)點應(yīng)當(dāng)修建在什么地方，才能夠使它距離A、B兩個社區(qū)的距離之差最小？小紅根據(jù)街道的實際情況，以街道為標(biāo)準(zhǔn)建立X軸，建立如下坐標(biāo)系，測得A點的坐標(biāo)為（0，3），B點的坐標(biāo)為（6，5），假設(shè)居民服務(wù)點的坐標(biāo)為點Z，那么從A、B兩個點到居民服務(wù)點距離之差|AZ-BZ|的最大值是___。

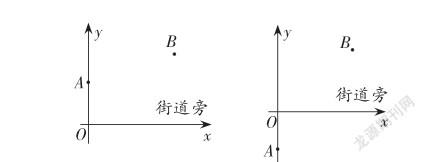
問題情境二：要在某街道旁邊修建一個居民服務(wù)點，向A，B兩社區(qū)提供便利服務(wù)，那么居民服務(wù)點應(yīng)該建在哪個地方才能使A、B到居民服務(wù)點的距離之差最短？小紅根據(jù)實際情況，以街道旁作為X軸，建立如下平面直角坐標(biāo)系，已知A的坐標(biāo)為（0，-3），B的坐標(biāo)是（6，5），假設(shè)居民服務(wù)點的坐標(biāo)為Z，那么從A、B兩點到便民服務(wù)點Z的距離之差|AZ-BZ|的最大值是___。

兩個情境的設(shè)置難度層層遞進，在情境一之中，為學(xué)生呈現(xiàn)的問題背景相對簡單，AB兩個頂點都在動點軌跡的同一側(cè)，X軸是動點軌跡，需要學(xué)生動手畫圖操作，觀察移動點位置發(fā)生的變化，并且借助三角形三邊關(guān)系的知識點就可以解答這一問題[2]。而在情境二之中，所設(shè)定的AB兩個定點是位于動點的兩側(cè)，此時的X軸是動點軌跡，學(xué)生在進行問題解答時，需要借助直觀想象、邏輯推理，并建立數(shù)學(xué)模型，將情境二轉(zhuǎn)變?yōu)榍榫骋坏膯栴}背景后再進行解答，在這一過程之中，學(xué)生需要多加思考，利用所學(xué)知識簡化問題情境，將復(fù)雜的問題簡化為熟悉的內(nèi)容，學(xué)生的解決問題能力才能得到提升。

2.重視認知結(jié)構(gòu)生成的過程，重視學(xué)生對數(shù)學(xué)思想的感悟

數(shù)學(xué)復(fù)習(xí)課更要關(guān)注學(xué)生數(shù)學(xué)思維的形成，在利用數(shù)學(xué)知識解答問題時注重其中蘊含著的數(shù)學(xué)思想的感悟與收獲，關(guān)注學(xué)生在復(fù)習(xí)課中數(shù)學(xué)思想的積淀與形成。這就要求教師要在課程建構(gòu)的過程中重視活動環(huán)節(jié)的多樣化，學(xué)生在多種類型的基本活動中運用數(shù)學(xué)知識，收獲數(shù)學(xué)思想，提升數(shù)學(xué)核心素養(yǎng)。

例如，在復(fù)習(xí)《直角三角形的存在性》時，教師可以讓學(xué)生在課前做好自主回顧復(fù)習(xí)工作，總結(jié)與直角三角形相關(guān)的數(shù)學(xué)知識，并嘗試以思維導(dǎo)圖的形式初步建構(gòu)起自己腦海中的知識體系。在課堂的第一環(huán)節(jié)讓學(xué)生以小組為單位進行學(xué)習(xí)結(jié)果的交流分享，在學(xué)習(xí)分享中互相幫助，共同完善數(shù)學(xué)思維體系，教師進行適時的指導(dǎo)。第二環(huán)節(jié)，教師為學(xué)生設(shè)置問題情境，并要求學(xué)生進行獨立思考，根據(jù)自己梳理的知識體系尋找問題解決的方法，體會數(shù)學(xué)思想。第三環(huán)節(jié)，學(xué)生進行分享交流。最后，教師指導(dǎo)學(xué)生多角度思考數(shù)學(xué)問題，再次完善思維體系深化數(shù)學(xué)感悟。

三、總結(jié)

通過科學(xué)有序的復(fù)習(xí)課堂，引導(dǎo)學(xué)生回顧梳理學(xué)習(xí)過的數(shù)學(xué)知識，將所學(xué)的知識點系統(tǒng)化、結(jié)構(gòu)化，在腦海中建構(gòu)起合理的數(shù)學(xué)知識體系，在這一過程中學(xué)生動手動腦探究、思考和實踐，學(xué)生的數(shù)學(xué)核心素養(yǎng)能夠得到有效的鍛煉與提升。

參考文獻：

[1]黃悅軍，劉明軍，田明剛.核心素養(yǎng)視角下的初中數(shù)學(xué)專題復(fù)習(xí)課教學(xué)[J].上海中學(xué)數(shù)學(xué)，2018（9）.

[2]朱立明，胡洪強，馬云鵬.數(shù)學(xué)核心素養(yǎng)的理解與生成路徑——以高中數(shù)學(xué)課程為例[J].數(shù)學(xué)教育學(xué)報，2018（1）.

（作者單位：浙江省樂清市虹橋鎮(zhèn)第一中學(xué)325600）